无杆臂误差快速传递对准方法

蒋文钟，戴洪德，孙玉玉，吴晓男

（1.92214部队，浙江 宁波 315826；2.海军航空工程学院 a.控制工程系；b.政治部，山东 烟台 264001）

惯性导航系统的初始对准按载体的运动状况分为静基座对准和动基座对准[1-3]，舰载或机载装备惯导系统的初始对准是典型动基座对准，动基座对准的首选方案就是充分利用载体主惯导信息的传递对准，传递对准大多选用主子惯导间的速度误差作为量测信息，但是以速度作为量测时，载体的角运动会使得主子惯导间的速度存在因为安装位置不一致而引起的杆臂误差[4-5]，该误差会引起较大的失准角估计误差，在传递对准时必须对杆臂误差进行准确的补偿[6-7]。但是载体变形的存在又使得杆臂误差的准确补偿存在较大的困难。针对这一问题，本文研究了基于美国学者Kain 提出的快速传递对准误差模型[8]的无杆臂误差快速传递对准方法，以主子惯导间的姿态信息和角速度信息作为传递对准的匹配量，用角速度信息代替速度信息作为传递对准卡尔曼滤波器的量测，这样就可以避免原来量测信息中的杆臂误差补偿，也就避免了由于变形引起杆臂长度变化而带来的误差。最后进行了计算机仿真，仿真结果验证了该方法的有效性。

1 快速传递对准误差模型

上世纪八十年代末，美国学者Kain 提出的快速传递对准方案开启了快速传递对准的新时代[8]，并在实际装备上进行了试飞实验[9]，引起了其他研究者的重视[10-12]。

在传递对准过程中，当没有主子惯导对准误差、主子惯性器件误差的理想情况下，主惯导相对导航坐标系的方向余弦矩阵（DCM）Cmn和子惯导相对导航坐标系的方向余弦矩阵应该是一致的，于是在直观上这两个方向余弦矩阵之间的差别就表示对准误差与器件误差的测量结果。所以定义：

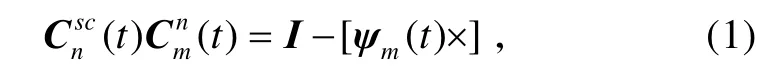
式中，ψm(t)（假设为小角度）表示主子惯导系统坐标系之间随时间变化的误差角度。因为在传递对准的开始时刻，用主惯导的数据对子惯导进行一次装订完成粗对准[2，8]，所以我们有即在初始时刻，子惯导的方向余弦矩阵与主惯导的方向余弦矩阵相等。因此，

在此基础上，Kain在文献[8]中给出如下的速度误差和姿态误差传播微分方程：

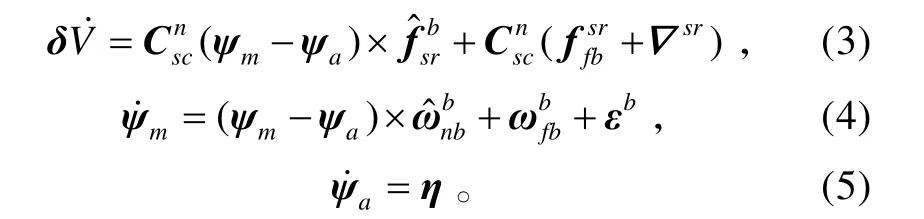
本文所提出的基于姿态信息和角速度信息匹配的无杆臂误差补偿快速传递对准正是基于该误差模型。

2 快速传递对准量测模型

为了避免使用速度量测而必须进行杆臂误差补偿，引入了角速度量测来进行快速传递对准时的失准角估计。Robert M.Rogers在文献[13]中研究了“速度+角速度”匹配快速传递对准算法，并对分别采用速度量测、角速度量测和“速度+角速度”量测的传递对准效果进行了分析对比，仅采用速度量测时对准精度只能达到4 mrad的精度，仅采用角速度量测时东向对准精度较低，而采用组合量测时可以在10 s内达到1 mrad 左右的精度。黄昆和杨功流等研究了舰载传递对准时的姿态加角速度匹配传递对准，来估计舰船甲板的变形和陀螺常值漂移[14]。我们采用了常规快速传递对准中的姿态信息来配合角速度完成高精度的快速传递对准。下面分别介绍姿态量测模型和角速度量测模型。

2.1 姿态量测模型

在传递对准过程中，主子惯导系统的姿态信息可以分别由各自系统的导航解算获得，也就是计算姿态值。根据式(1)可以由主子惯导系统的方向余弦矩阵获得姿态量测值ψm(t)，而这正是误差模型(4)所描述的量。

2.2 角速度量测模型

假设主惯导的角速度测量值为

子惯导的角速度测量值为

子惯导陀螺仪的输出可以表示为真实角速度和挠曲变形角速度以及陀螺测量误差之和，当认为主惯导没有误差时，真实角速度又可以用主惯导测量值在子惯导坐标系内投影值来表示[7]，则：

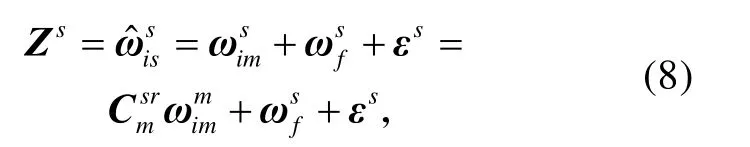
所以角速度量测差值可以写为：

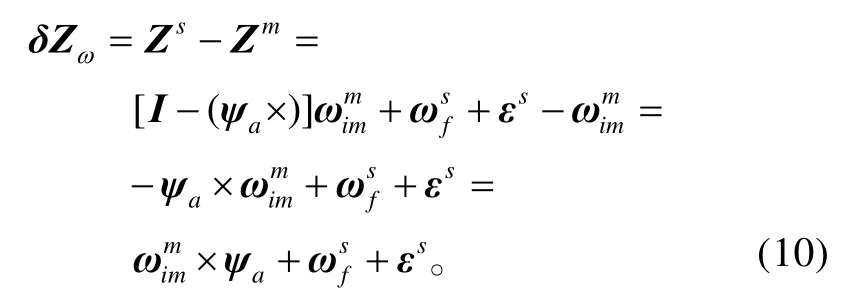
这里的角速度量测模型和前面的姿态量测模型构成了我们快速传递对准时的匹配量，这两个量测信息都不包含杆臂误差，所以也就不需要对杆臂误差进行补偿。

3 快速传递对准滤波器设计及仿真分析

3.1 快速传递对准系统模型

根据前面关于快速传递对准误差模型和快速传递量测模型的分析，可以列为卡尔曼滤波器状态的变量有：速度误差、计算姿态误差、真实姿态误差，虽然还可以把其他的一些量列入状态空间，比如陀螺漂移、加速度计零偏、陀螺刻度系数误差、加速度计刻度系数误差、挠曲变形参数等。但是，这样卡尔曼滤波器的阶数就会很高[1]，为了减少计算量，增强实时性，考虑到工程应用的可实现性，必须对卡尔曼滤波器的状态进行删减。首先，简化描述挠曲变形的状态，而用加入补偿白噪声过程来代替；其次，对于快速传递对准，整个过程不超过1min，而惯性器件的误差需要很长的时间才能对量测值产生影响，这样在快速传递对准的短时间内就不能精确估计出惯性器件的误差，所以对惯性器件的误差也进行了删减。

快速传递对准动态系统状态空间模型可以表示为：

状态向量为：

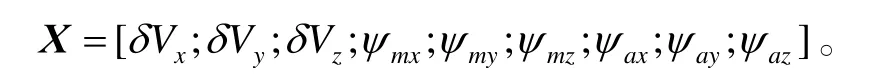
观测向量为：

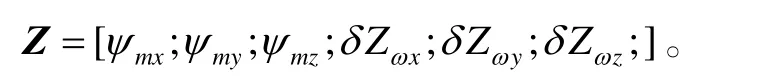
状态一步转移矩阵A根据式(3)、(4)和式(5)列写。

量测矩阵H根据前面的姿态量测模型和角速度量测模型表示为：

其中，姿态量测矩阵表示为Hϕ=[03×3,I3×3,03×3]，而根据式(10)，角速度量测矩阵可以表示为

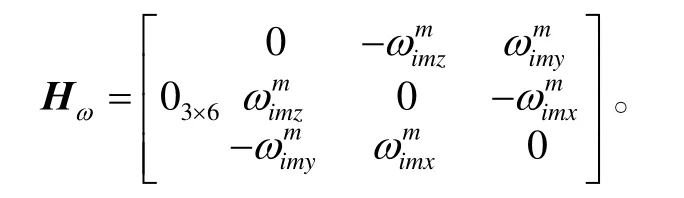
系统噪声矩阵 B=I9×9，w和v分别为系统噪声和量测噪声，观测值根据主、子惯导系统的相关参数由式(1)、式(10)获得。根据量测值应用卡尔曼滤波递推估计算法就得到失准角的实时估计。

3.2 传递对准仿真分析

为了验证本文所提方法的有效性，进行了本文所提方法和常规“速度+姿态”匹配快速传递对准方法的仿真对比，并分别在无杆臂误差及杆臂长度存在20%误差的条件下进行了仿真分析。仿真时，取主子惯导间固定安装误差为[1,1,2]Tdeg，总对准时间为20 s。

当杆臂速度能够得到准确补偿时，“姿态+角速度”快速传递对准和常规“速度+姿态”快速传递对准失准角估计误差见图1。

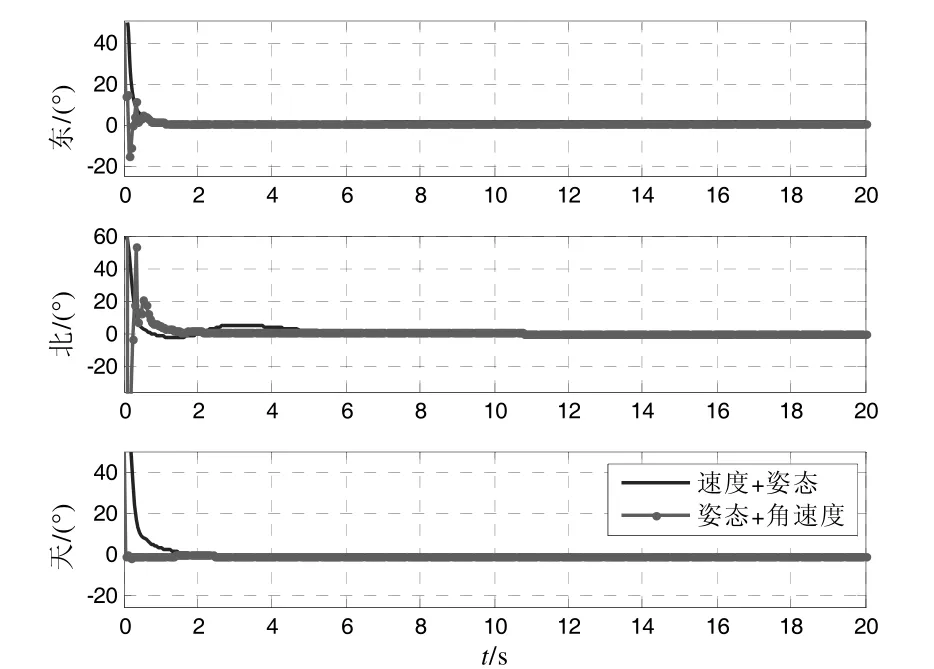
图1 传递对准失准角估计误差(杆臂长度准确)

从图1可以看出，当杆臂误差能够得到准确补偿时，“速度+姿态”匹配快速传递对准具有较好的失准角估计精度和速度，本文提出的“姿态+角速度”也具有较快的估计速度，特别是天方向的估计速度提高最明显，精度和“速度+姿态”相当。

当杆臂长度存在20%的误差时，“姿态+角速度”快速传递对准和常规“速度+姿态”快速传递对准失准角估计误差见图2。

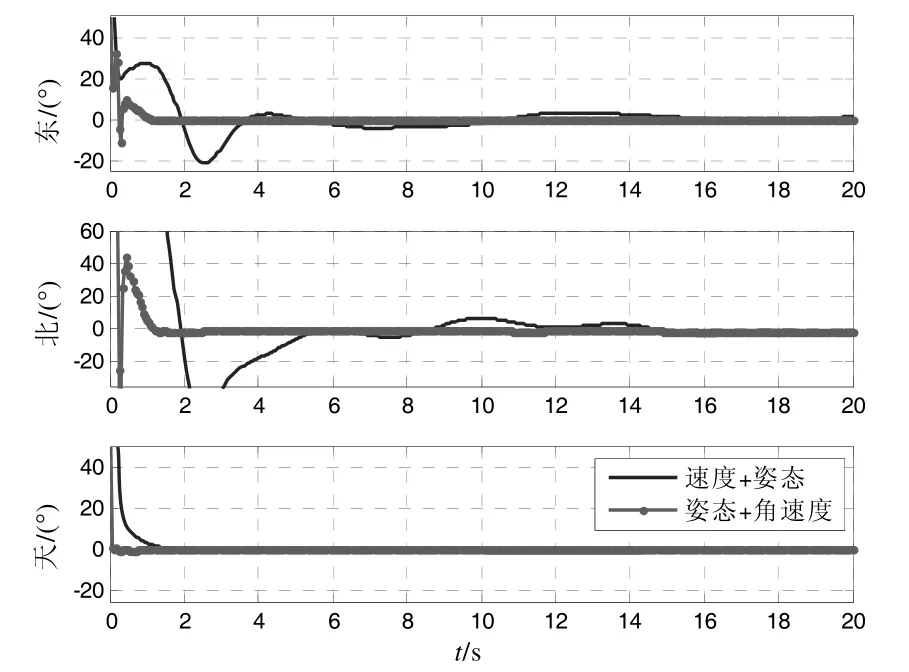
图2 传递对准失准角估计误差(杆臂有20%误差)

从图2中可以看出，当杆臂长度不准确时，“速度+姿态”匹配快速传递对准受到了较大的影响，而本文提出的“姿态+角速度”匹配快速传递对准所受的影响却相对较小，依然能够在10 s 内以较高的精度收敛。

4 小结

本文介绍了一种无杆臂误差补偿的快速传递对准方法。该方法基于美国学者Kain 提出的快速传递误差模型，采用“姿态+角速度”匹配作为快速传递对准的量测信息，避免了使用速度量测时的杆臂速度误差补偿不准确引起的传递对准精度下降的问题。仿真结果表明，该方法能够在杆臂误差较大时获得较高的失准角估计精度。

[1]万德钧,房建成.惯性导航初始对准[M].南京:东南大学出版社,1998:9-10.

[2]TITTERTON D H,WESTON J L.Strapdown Inertial Navigation Technology[M].2 ed.The Institution of Electrical Engineers,2004:270-300.

[3]秦永元.惯性导航[M].北京:科学出版社,2006:263-280

[4]徐晓苏,万德钧.杆臂效应对捷联惯性导航系统初始对准精度的影响及其在线补偿方法研究[J].中国惯性技术学报,1994,2(2):22-27.

[5]江红,张炎华,赵忠华.捷联惯性导航系统传递对准的杆臂效应分析[J].中国造船,2006,47(4):71-75.

[6]高青伟,赵国荣,王希彬,等.传递对准中载舰挠曲变形和杆臂效应一体化建模与仿真[J].航空学报,2009,30(11):2172-2177.

[7]戴洪德,陈明,周绍磊,等.一种新的动基座快速传递对准方法及其可观测度分析[J].宇航学报,2009,30(4):1449-1454.

[8]KAIN J E,CLOUTIER J R.Rapid transfer alignment for tactical weapon applications[C]//AIAA Guidance,Navigation and control Conference.1989:1290-1300

[9]SHORTTELLE K J,GRAHAM W R,RABOURN L C.F-16 flight tests of a rapid transfer alignment procedure[C]//IEEE Position Location and Navigation Symposium.1998:379-386.

[10]TAKASHI MORIMOTO,KOHEI OHTSU.Initial Rapid Alignment Calibration of a Marine Inertial Navigation System[C]//IEEE Position Location and Navigation Symposium.1994∶348-354.

[11]JAN WENDEL,JURGEN METZGER,GERT F TROMMER.Rapid transfer alignment in the presence of time forrelated measurement and system noise[C]//AIAA Guidance,Navigarion,and Control Conference and Exhibi.2004∶1-12.

[12]HAO YANLING,XIONG ZHILAN,WANG WEI,et al.Rapid transfer alignment based on unscented Kalman filter[C]//Proceedings of the 2006 American Control Conference.2006∶2215-2220.

[13]ROBERT M ROGERS.Velocity-plus-rate matching for improved tactical weapon rapid transfer alignment[C]//AIAA Guidance,Navigation and Control Conference.1991∶1580-1588.

[14]黄昆,杨功流,刘玉峰.舰载姿态加角速度匹配传递对准方法研究[J].中国惯性技术学报,2006,14(1)∶17-20.