多操纵面飞机稳定非线性控制分配

李 恒，张友安，于进勇，李新辉

（1.海军航空工程学院控制工程系，山东 烟台 264001；2.71901部队，山东 聊城 252000）

目前，控制分配方法主要包括非优化的控制分配方法和优化的控制分配方法两大类。非优化的控制分配方法一般具有计算量小、工程易实现等优点，但缺少对操纵面偏转有效性的评估，不能充分利用各操纵面的操纵效率，如直接分配法[1]、广义逆法[2]和串接链法[3]等；优化的控制分配方法能够综合考虑操纵面的气动效率、位置约束和速率约束等因素，但计算量较大，很难满足工程应用的实时性要求，如线性规划[4]、二次规划[5]、序列二次规划法[6]、动态分配法[7]、多目标非线性规划法[8]等。

上述方法将控制分配问题转化为静态优化问题，其主要优点是将控制系统设计过程模块化，缺点是计算量大，并且没有考虑控制分配的稳定性以及采用控制分配后闭环系统的稳定性问题。文献[9]针对水面舰船的非线性控制分配问题，利用控制李雅普诺夫方法设计基于优化的动态非线性分配方法，该方法保证了闭环系统的渐近稳定性，但并不能保证控制分配的稳定性，也没有考虑执行器的约束。

本文基于李雅普诺夫稳定性理论和不变集定理，考虑操纵面的位置约束，对多操纵面飞机设计一个由上层控制律和动态控制分配律组成的非线性控制器，并保证上层控制子系统、动态控制分配子系统和整个闭环系统都是渐近稳定的，对某多操纵面飞机的仿真结果验证了方法的有效性。

1 问题描述

当不考虑飞机操纵面偏转产生的气动力时，多操纵面飞机控制分配的任务是将期望的三维控制力矩合理地分配给各个操纵面。由于各个操纵面具有较强的耦合效应和非线性特性，操纵面的偏转与其生成的控制力矩不再是线性关系，因而需要采用非线性控制分配。具有m(m＞3)个操纵面飞机的非线性动力学方程为：

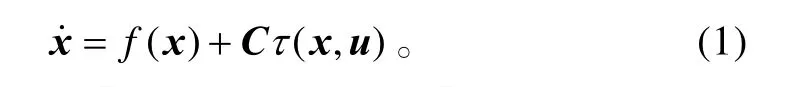
操纵面的位置约束可描述为：

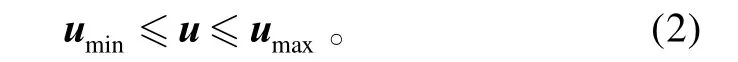
式(2)中：uimax、uimin分别为第i个操纵面的最大和最小偏转角，umin=[u1min,u2min,…,ummin]T，umax=[u1max,u2max,…,ummax]T。

控制的目的是使系统(1)渐近稳定跟踪给定期望轨迹 xd(t)。采用控制分配方法，视期望力矩 τd为虚拟控制，则系统(1)变为：

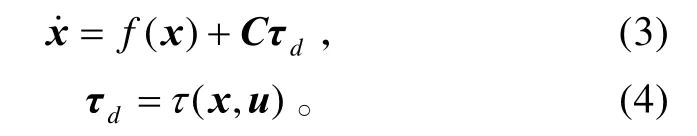
控制器设计分两步：第1步设计虚拟控制律 τd，使系统(3)的状态x 渐近稳定跟踪期望轨迹 xd(t)；第2步设计渐近稳定控制分配律，将 τd按式(4)的要求合理地分配给每个操纵面 δi，i=1,2,…,m。通过上述两步设计方法得出操纵面偏转量u后，还需要进一步验证整个闭环系统的稳定性。

在设计控制器前，不失一般性，先作如下假设。

假设1：期望轨迹 xd(t)是二阶连续可微的，则、存在。

假设2：期望力矩 τd在力矩可达集内，即满足式(4)的u 存在。

2 控制器设计

2.1 虚拟控制律设计

定义跟踪误差 xe=x−xd，取李雅普诺夫函数

对其沿式(3)求关于时间的导数有

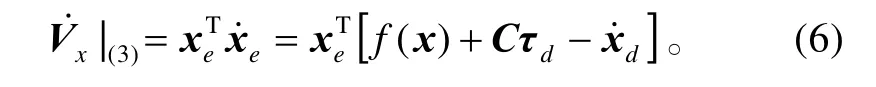
取虚拟控制律

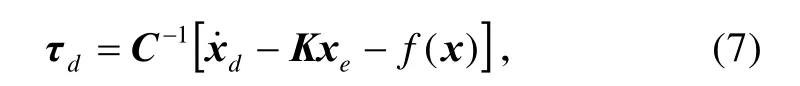
式中，K为3×3 维常数正定对角矩阵。

将式(7)代入式(6)有

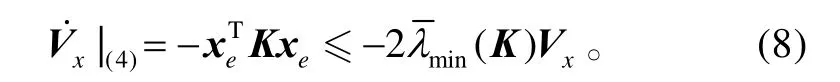
由李雅普诺夫稳定性定理知x 渐近趋近于 xd。

2.2 控制分配律设计

下面来设计控制分配律，使得虚拟控制律(7)在操纵面位置约束下满足式(4)。考虑性能指标函数J (x,u)，则控制分配问题可用以下的混合约束优化问题来描述：

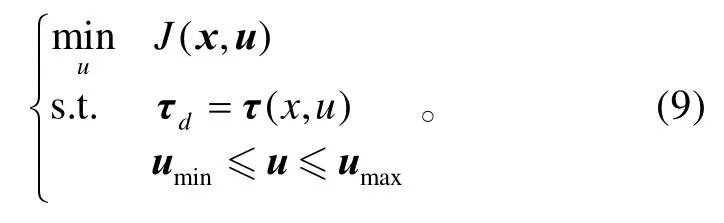
定义

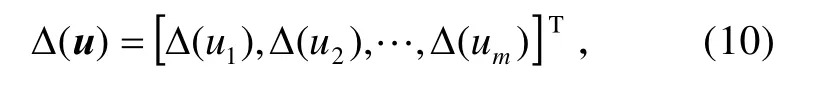
于是问题(9)等价于

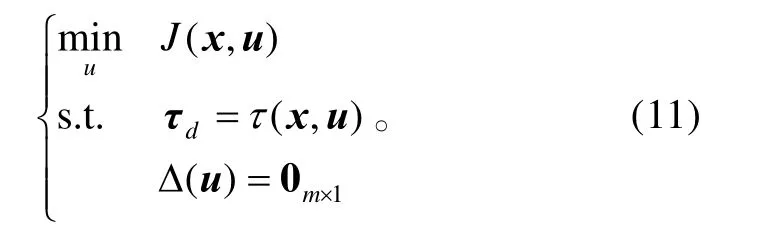
对等式约束优化问题(11)，采用拉格朗日松弛法求最优解，取拉格朗日函数为：

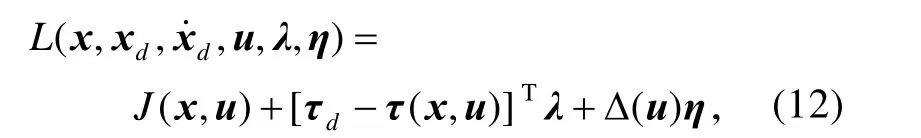
式中，λ∈R3，η∈ Rm为松弛变量。

定义最优集

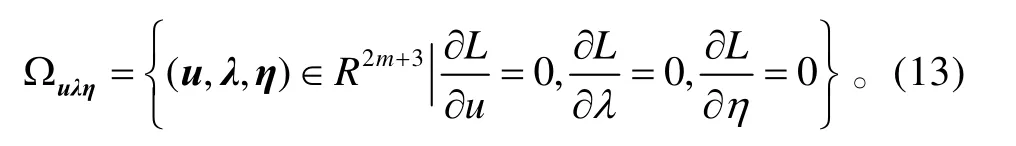
下面来设计控制分配律，使得(u,λ,η)是收敛至集合Ωuλη。

取李雅普诺夫型函数

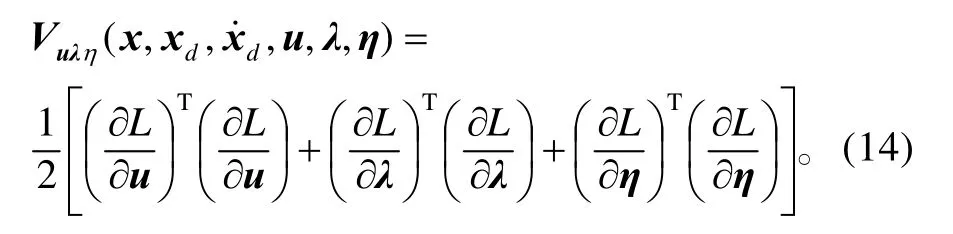
对其求关于时间的导数，则

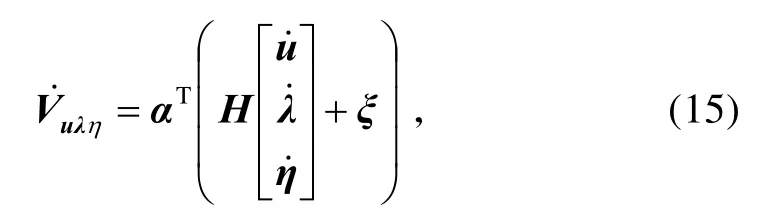
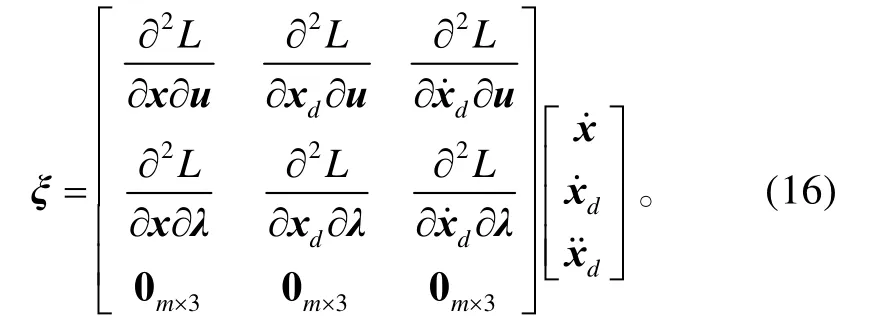
取控制分配更新律σ为小的正数，当σ足够小时，

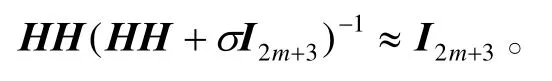
将式(17)代入式(16)得

式中：Γ为(2m+3)×(2 m+3)维常值正定对角矩阵，

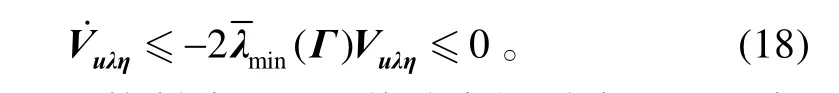
定理1：(控制分配子系统稳定性)在假设1和假设2的条件下，控制分配子系统(17)的状态(u,λ,η)渐近收敛至最优集Ωuλη。

证明：由式(18)得于是

设t=T时，(u,λ,η)到达Ωuλη，则t ≥T时，可知，集合Ωuλη为系统(17)的不变集。由LaSalle 不变集定理[11]知，(u,λ,η)渐近收敛至Ωuλη。

2.3 闭环系统稳定性

在得到虚拟控制律(7)和控制分配律(17)后，需要考虑由式(1)和式(17)组成的整个闭环系统稳定性。定义集合

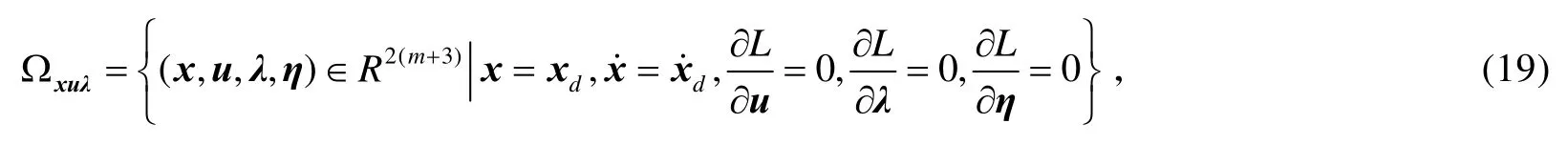
则下述定理成立。

定理2：(闭环系统稳定性)考虑系统(2)和系统(17)，在假设1和假设2的条件下，闭环系统的状态 (x,u,λ,η)渐近收敛至集合Ωxuλη。

证明：取李雅普诺夫函数对其求关于时间的导数，则

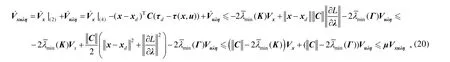
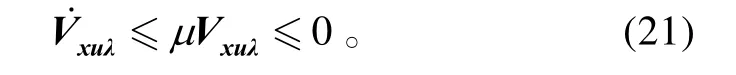
后面的证明过程同定理1。

3 仿真算例

方程为[12]：

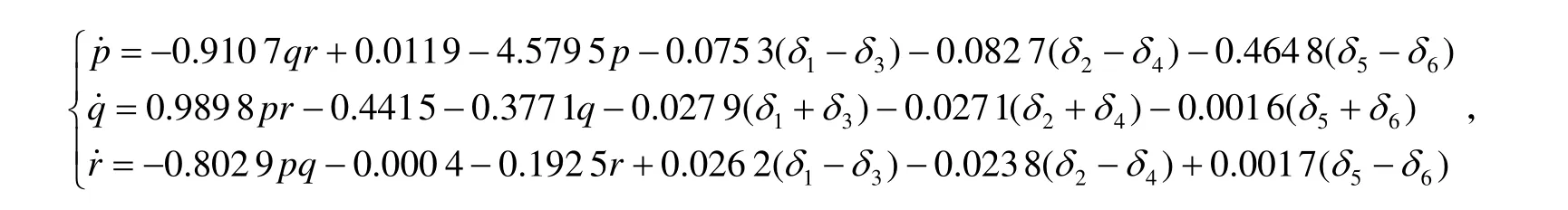
式中，操纵面偏转约束为uimin=−15°、uimax=15°，i=1,2,…,m。

选取参考输入为(单位(°)/s)：rc(t)=0；

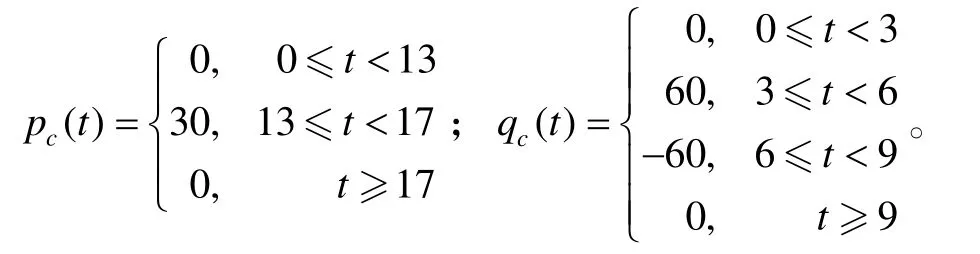
期望轨迹 xd(t)及其一阶、二阶导数通过对参考输入 xc(t)进行二阶滤波得到。滤波器传递函数为：其中，ωi=5为自然频率，ξi=0.707为阻尼系数。

仿真初始条件为：λ(0)=0m×1，η(0)=0m×1；控制器增益为K=5I3，Γ=10 I2m+3；Au=10−3I3，σ=10−6。仿真结果如图1～4所示。

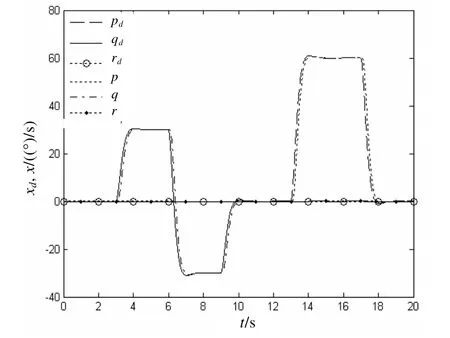
图1 p、q、r 跟踪性能

某型具有 m=6个操纵面飞机的非线性动力学

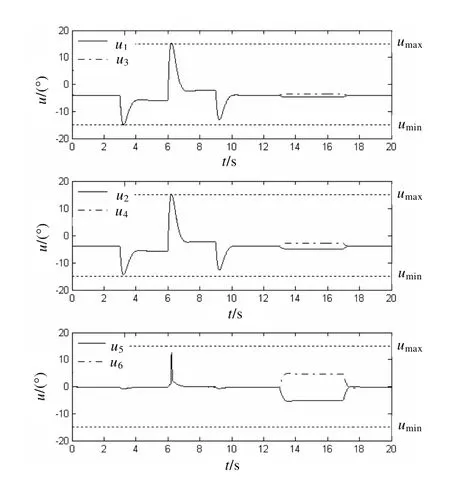
图2 各个控制面偏转角变化曲线

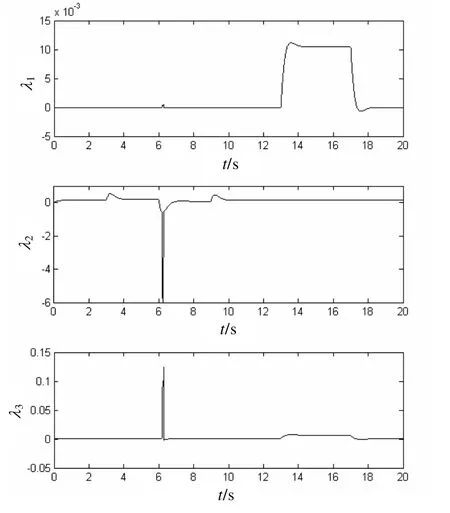
图3 松弛变量λ变化曲线

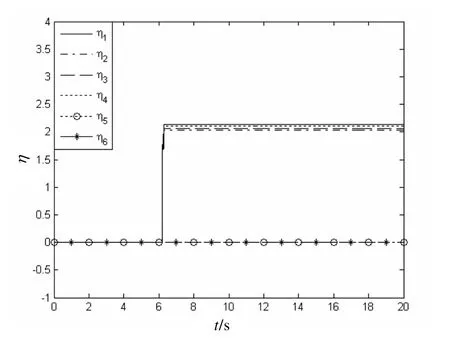
图4 松弛变量η变化曲线

由仿真结果可知，本文所设计的控制律和控制分配律能使多操纵面飞机的角速度 p、q、r 很好地跟踪期望轨迹。随着λ 趋于稳定，飞机的转矩达到期望转矩。t=6.18 s时，控制面偏转角 δ1、δ2、δ3、δ4到达饱和，此时 η1、η2、η3、η4不再为零，其作用是使饱和的控制面尽量减小，为达到期望转矩，需要增加 δ5、δ6偏转角，为此，λ 也相应变化。

4 结论

针对多操纵面飞机具有冗余操纵面的特点，本文基于李雅普诺夫稳定性理论和LaSalle 不变集定理，设计了一种由上层虚拟控制律和控制分配更新律组成的非线性控制方法。该方法能同时保证上层虚拟控制子系统、控制分配子系统和整个闭环系统的渐近稳定性，并能有效处理操纵面偏转角的位置约束。对某型多操纵面飞机的仿真结果验证了本文方法的有效性。

[1]DURHAM W C.Constrained control allocation[J].Journal of Guidance,Control,and Dynamics,1993,16(4):717-725.

[2]RANEY D L,MONTGOMERY R C.Flight Control Using Distributed Shape-Change Effector Arrays[R].AIAA 2000-1560,2000.

[3]BUFFINGTON J M,ENNS D F.Lyapunov stability analysis of daisy chain control allocation[J].Journal of Guidance,Control,and Dynamics,1996,19(6):1226-1230.

[4]LANGARI R,KRISHNAKUMAR K,GUNDYBURLET K.Neural network based modeling and analysis of LP control surface allocation[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Austin,2003.

[5]SIMMONS A T.Control Allocation Techniques using Existing and Novel Quadratic Programming Algorithms[D].Auburn,Alabama:Auburn University,2003.

[6]JOHANSEN T A,FOSSEN T I,BERGE S P.Constrained Nonlinear Control Allocation with Singularity Avoidance using Sequential Quadratic Programming[J].IEEE Transactions on Control Systems Technology,2004,12(1):211-216.

[7]LUO YU,SERRANI A,YURKOVICH S,OPPENHEIMER M W,et al.Model predictive dynamic control allocation scheme for reentry vehicles[J].Journal of Guidance,Control,and Dynamics,2007,30(1):100-113.

[8]杨恩泉,高金源,李卫琪.多目标非线性控制分配方法研究[J].航空学报,2008,29(4):995-1001.

[9]JOHANSEN T A.Optimizing Nonlinear Control Allocation[C]//Proceedings of the 43rd IEEE Conference on Decision and Control.Bahamas,2004:3435-3440.

[10]STEVENS B L,LEWIS F L.Aircraft Control and Simulation[M].2nd Edition.New Jersey:John Wiley &Sons,2003:109-110.

[11]KHALIL H K.Nonlinear Systems[M].3rd Edition.Beijing:Publishing House of Electronics Industry,2007:126-128.

[12]LIAO F,LUM K Y,WANG J L,et al.Constrained Nonlinear Finite-Time Control Allocation[C]//Proceedings of the 2007 American Control Conference.New York City,2007:3801-3806.