基于Hausdorff距离的反舰导弹目标选择方法
潘 哲
(海军装备部,重庆 400042)
导引头的目标选择技术是反舰导弹末制导中的核心技术,直接制约导弹作战效能的发挥。目前,主动末制导雷达反舰导弹对目标的选择主要有距离选择区法和扩展搜索图选择法,这些方法的实质是人工射前瞄准选择目标,受导弹自控终点的散布误差和目标的机动影响较大,因而不适合应用于超视距反舰导弹。依据高技术战场的迫切需求,反舰导弹已在射程和搜索能力上实现由视距向超视距的跨跃,亟待解决的问题是如何正确选择预定目标[1]。
文献[1]提出了一种利用舰艇编队相互位置关系的预定目标选择方法。文献[2-3]所研究的目标选择方法中也利用了编队的相互位置关系,且其理论依据与文献[1]类似。由于利用了编队形状,该类方法可实现打击任意指定目标的战术意图,并具备一定的抗干扰能力,而且不受一致运动(包括自控终点散布误差和编队整体机动)的影响。但该类方法在比较两个编队的相互位置关系时,需要根据经验或试验事先获得一个门限值[1]。此外,文献[4]利用了部分Hausdorff距离(PHD)序列的二阶差分的最大值来剔除远处干扰点,但同样需要事先根据经验设定一个门限。
如果门限选小了,就可能误将相似部分剔除掉,如果选大了,就不能较好地剔除外部点的干扰,因此,上述方法都面临门限选择困难的问题。
本文基于Hausdorff距离提出一种新的部分匹配途径,以自适应剔除干扰并保留形状相似部分的作用,从而获得一种抗干扰能力更好的预定目标选择方法。
1 问题描述
设反舰导弹发射平台的火控雷达探测到远距离处的一个舰艇编队A(如图1所示,这里给出了3种编队队形,每个编队中的各舰艇用ai表示)。依据战术任务要求,反舰导弹的攻击目标为a1。在导弹发射时刻,通过发射平台的火控系统向导弹装订由火控雷达探测到的编队目标的位置信息,并对预定目标进行标记。经过自控段后,末制导雷达开机,雷达在其最大搜索区域搜索一遍,录入所有探测到的目标信息,然后进行预定目标选择。预定目标选择的任务就是使末制导雷达开机后捕获到a1,而非其他目标。
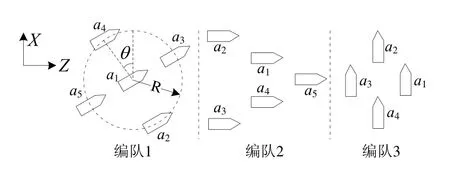
图1 舰艇编队
火控雷达装订的编队信息和末制导雷达搜索得到的编队信息都可以用平面上的点集来描述。预定目标选择实际上是对应点的匹配,即从末制导雷达获得的点集中寻找火控雷达装订目标点(即预定目标)的对应点。
以往基于Hausdorff距离的众多部分匹配方法都不能自动给出最相匹配的部分形状。有的需要根据经验或试验给出L0和K0的估计值L和K,如Huttenlocher 等人提出的双向部分Hausdorff距离[5],Tan 等人通过引入平均算子提出的LTS-HD[6],Paumard 等人提出的CHD[7],Han 等人提出的HDEP[8],以及Rucklidge 用一个包含模板中有用形状的矩形框来确定L和K的方法[9]。有的需要通过设定一个门限来剔除外部点的影响,如Kwon 改进的M-HD[10]以及Huttenlocher 等人利用给定门限下的Hausdorff 分数作为形状的相似性度量的方法[11]。
由于探测概率、虚警概率因不同的编队目标的特征以及不同的海情而不同,并且敌方编队释放冲淡干扰的情况更是未知的,因而不可能事先准确获知L0和K0。以往的诸多部分匹配理论应用实例中,形状是由大量的点构成,一般通过事先大致估计得到L和K的取值。此时,由于(L−L0)/p以及(K−K0)/q很小,因而对匹配结果的影响较小。但本文研究中,A和B是由少量稀疏的点构成,如果通过事先大致估计得到L和K的取值,由于(L−L0)/p以及(K−K0)/q较大,会显著增大匹配误差。
本文通过定义一种新的部分Hausdorff距离提出了一种新的部分匹配途径。该新途径下不需要事先确定L和K的值,也不需要通过设置门限来剔除外部点(其定义见2.2节),而是逐个剔除最能引起两个形状不相似的外部点,自适应获取最优L0和K0。
此外,进行部分匹配时需要获得两个点集在所有可能的平移和旋转变换下的“最小距离”。对于两个编队之间的平移和旋转变换,可用刚体变换来统一描述。“最小距离”对应的刚体变换就是“最佳匹配位置”。因此,获取“最小距离”的过程也是搜索“最佳匹配位置”的过程。为了减轻计算负担,本文设计一种二级匹配模型来搜索最佳匹配位置。在最佳匹配位置下,两个点集的对应点之间距离最近,因而可在此最佳匹配位置下采用最近邻准则获取对应点,从而实现预定目标选择。本文采用了双向最近邻准则来选择对应点以提高选择结果的正确概率。
2 部分匹配
2.1 Hausdorff距离
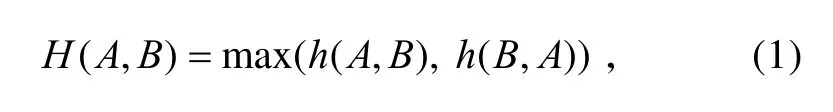
其中,
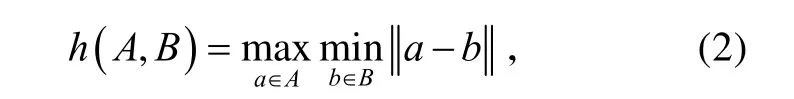
h(A,B)称为从A到B的单向Hausdorff距离。它对A中各个点按照其到B中最近点的距离进行了有效的排序,并用最大值点(也就是A中最不匹配的点)作为结果距离。同理可定义从 B到A的单向Hausdorff距离h(B,A)。H(A,B)是h(A,B)和h(B,A)的最大值,通过测量A中到B中任何点距离最远的点,以及测量B中到A中任何点距离最远的点,H(A,B)就度量了A、B之间的不匹配程度。
从A到B的部分Hausdorff距离为
对于给定的点集A和B,Hausdorff距离[5]定义为:
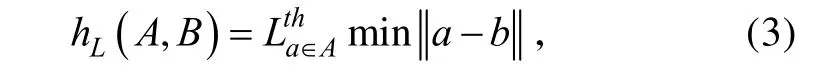
其含义是:对于A中等每个点,计算它到B中与之距离最近点的距离,然后按照这个距离值对A中的所有点进行排序,并选取序列的第L个值作为结果。可见hL(A,B)自动从A中选择了L个最佳匹配点。同理可定义从B到A的部分Hausdorff距离hK(B,A)。
2.2 部分匹配新途径
两个存在部分相似性的点集A和B,必然存在A中L0个点构成的子集 0LA与B中K0个点构成的子集BK0之间最相似,于是L0和K0就是K和L的最优值。称构成 0LA和BK0的点为“共同点”,其余点为“外部点”。共同点表示了形状的相似部分,外部点表示了引起形状不相似的那些点,匹配过程希望保留共同点,同时剔除或削弱外部点的影响。
假设给定的点集A和B 已处于最佳匹配位置(搜索最佳匹配位置的方法将在3.2节介绍),若h(A,B)>h(B,A),说明最能引起A、B不相似的点在A中,否则在B中。如果最能引起A、B不相似的外部点在A中,剔除它之后,A中剩余点构成的形状与B的不相似程度应减小;如果最能引起A、B不相似的外部点不在A中,剔除A中一个点后,A中剩余点构成的形状与B的不相似程度不会减小;如果A和B中不存在外部点,那么从A中剔除任何一个点(也就是剔除了一个共同点)后,A中剩余点构成的形状与B的不相似程度一定会增大。基于上述事实,定义从A到B的新的部分Hausdorff距离(New Partial Hausdorff Distance,NPHD)为
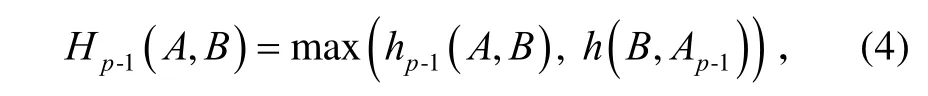
式中,Ap-1为由hp-1(A,B)所确定的A的子集,Hp-1(A,B)的作用是考察从A中去掉一个点后对两个形状相似程度的影响。
首先计算hp-1(A,B),获得剔除A中一点后的剩余部分 Ap-1,然后计算 B到Ap-1的不相似程度h(B,Ap-1),取h(B,Ap-1)和hp-1(A,B)的最大值为剔除A中一点之后两个形状的不相似程度,即Hp-1(A,B)。若Hp-1(A,B)
以往定义的hL(A,B)可以获得A中的一系列子集AL(L=1,…,p−1),但hL(A,B)不能检测出剔除共同点的操作。在NPHD 定义中通过计算h(B,Ap-1),使得剔除共同点的操作得以体现。因此在NPHD 定义下,任何破坏两个形状相似性的部分形状增减都会通过它体现出来。
同样可以定义从B到A的NPHD为:
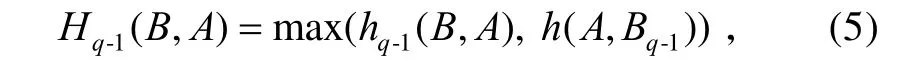
式中,Bq-1为由hq-1(B,A)所确定的B的子集,Hq-1(B,A)的作用是考察从B中去掉一个点后对A、B形状相似程度的影响。
基于上述NPHD的定义,可通过如下程序逐个剔除最能引起两个点集不相似的点,最终获取最佳的部分形状。
1)初始化。让A、B作为初始处理点集,计算h(A,B)、h(B,A)和H(A,B)。
2)若h(A,B)>h(B,A),则转至3),否则转至4)。
3)从A中剔除外部点。计算hp-1(A,B)、h(B,Ap-1)和Hp-1(A,B),若:① Hp-1(A,B) 4)从B中剔除外部点。计算hq-1(B,A)、h(A,Bq-1)和Hq-1(B,A),若:① Hq-1(B,A) 上述部分匹配途径无需事先人工设定任何参数。且由于NPHD 能检测到最能引起两个形状不匹配的点,通过不断检测并剔除最能引起两个形状不匹配的点就可以减少外部点的干扰,同时NPHD 能够敏感于剔除共同点的操作,确保不损失形状的相似信息,因此能够自动获取最优部分形状 AL0和BK0。 在导弹惯性导航期间,由于舰艇编队整体可能存在一致平移运动,并且弹上导航系统存在导航位置误差,因此XOZ 平面上的两个点集存在位置平移,又由于编队整体可能的一致转向运动,弹上导航系统存在导航姿态误差,并且发射平台的导航设备与弹上导航设备存在初始对准误差,因而这两个点集还存在位置旋转。这两个点集之间的平移和旋转可以统一用刚体变换来描述。 NPHD 用来度量两个固定位置点集之间的距离。对于存在刚体变换的两个点集,所关心的是所有可能的匹配位置下的最小NPHD。刚体变换下的最小NPHD 定义为 和 式中:t为加在A中各点的平移量;θ为施加在A中各点的旋转量;⊕为标准的闵可夫斯基(Minkowski)求和符号,也就是说A⊕t={a+t|a∈A};Rθ为旋转矩阵;最小NPHD 所对应的t和θ就是最佳匹配位置。 为了获得各种可能的刚体变换下的最小NPHD和最佳匹配位置,提出二级匹配模型:粗匹配和精匹配。首先,是进行粗匹配。粗匹配过程又分为3步,第一步是获得可能的平移;第二步是从这些可能平移上找到最可能是最佳匹配位置的刚体变换位置;第三步是从这些可能是最佳匹配位置的刚体变换位置中计算NPHD最小的位置。然后,进行精匹配。在粗匹配得到的最佳匹配位置附近寻找更优的匹配位置,是对粗匹配结果的微调,且精匹配过程又可分2个步骤实现。下面详细阐述上述5个实现步骤。 第一步:获取粗匹配的可能平移。 某一次剔除外部点的操作中,设A中元素个数为M(M≤p),B中元素的个数为N(N≤q)。首先,假设A中的某一点a在B中存在对应点。平移A 使a与B中的每一个点重合就可构成N个平移,这其中一定包含了a与其B中对应点重合的情况。如果A、B之间不存在旋转,那么这个使对应点重合的平移一定是这N个平移中最接近最佳匹配位置的一个。尽管A中有M个点,但只需要其中一个在B中存在对应点的点进行N次平移就可以找到近似的最佳匹配位置。但通常无法保证这个任意选取的A中的点在B中一定存在对应点。如果所选择的a 由于某种原因在B中没有出现,也就是说它在B中不存在对应点,那么这N个平移都将偏离最佳的匹配位置较大的距离。为了确保所选择的A中的点至少有一个在B中存在对应点,可以从A中选择多个(M0个)点,将这些点分别平移到与B中的每个点重合,显然会有M0⋅N个平移。M0的取值可根据火控雷达获取目标信息时可能的海面干扰情况以及末制导雷达的探测概率大致确定。若火控雷达探测编队时海面不存在冲淡干扰,且末制导雷达对目标的探测概率为1,可以取M0=1,否则需要增大M0。当M0=M时,可以肯定至少存在一个组对应点,除非末制导雷达根本没有探测到任何真实的目标。 第二步:获取粗匹配的可能刚体变换位置。 对于第一步获取的M0⋅N个平移,每个平移位置上还需要考虑旋转。每个平移都是由A中某点平移到与B中某点重合的结果。取该平移上的旋转中心为其所对应的A中的点。假设A和B之间最大的可能旋转变化为其中,dθ1是旋转步长,i=−Nc1∶1∶Nc1为旋转系数。平移与旋转组合后构成M0⋅N⋅(2Nc1+1)个刚体变换位置。 仿照文献[12]的方法,可从所有的刚体变换中找到那些是最佳匹配位置的可能性较大的位置,并存储它们,随后在这些存储的位置上应用NPHD,从中找出最佳的匹配位置。对于某一个刚体变换位置,对A中的每一个点a 定义一个以该点为中心、半边长为ρ(本文取3 km)的正方形邻域,如果有B中的点位于此邻域内,就称a在B中存在对应点。定义 式中,r为小于1的测量系数,可根据经验或试验给出,本文取0.6。 如果某一个刚体变换位置下A中有对应点的元素个数大于Ms,那么这个刚体变换位置就添加到可能的最佳匹配位置数组中。对每一个位置进行以上操作,最后剩下的可能最佳匹配位置相对M0⋅N⋅(2N1c+1)要小得多。 在本文的仿真实验中,对图1中的3个编队情形,通过该措施筛选出来的最佳匹配位置分别只占M0⋅N⋅(2N1c+1)个刚体变换位置的26.16%、27.47%和27.62%。由于计算Ms(仅包含比较运算)的耗时小于计算NPHD(包含乘法运算)的耗时,本文仿真实验中,采用该措施后,针对图1中3个编队的预定目标选择算法平均耗时降低了41.46%。 第三步:获取最佳粗匹配位置。 对第二步获取的每一个可能的最佳匹配位置计算 NPHD,进行部分匹配(剔除外部点),并选择NPHD最小的位置作为最佳粗匹配位置。 第四步:选取精匹配的可能匹配位置。 粗匹配过程剔除了部分外部点,且将模板中的点整体平移和旋转到了很接近最佳匹配的位置。但为了进一步剔除外部点,并使各个对应点之间的距离更加接近,需要在最佳粗匹配位置附近搜索更优的变换位置。如果说粗匹配过程是一个粗调过程,那么精匹配过程就是一个微调过程。取两个坐标轴方向上的平移范围为±(Nt⋅dx)和±(Nt⋅dz),dx和dz为步长,i=−Nt∶1∶Nt为平移系数。 第五步:获取最佳匹配位置。 对精匹配时选取的每一个可能的匹配位置计算NPHD,进行部分匹配(进一步剔除外部点),并选择NPHD最小的位置作为最佳匹配位置。 获取最佳匹配位置的过程就是不断将A中的点移动到B中对应点附近的过程。因此,在最佳匹配位置下,对于A中的每一点,B中与之距离最近的点最可能是其对应点,反之亦然。 实现预定目标选择,实际上就是进行对应点的配对,为了提高所选择结果的正确概率,本文采用双向最近邻准则来获取对应点,即对于A中的某点a,在最佳匹配位置下,可得到B中距离a最近的点为b,若同时A中距离b最近的点为a,那么a和b是对应点,否则不然。 这种双向最近邻准则可以处理A中的预定目标在B中没有出现的情况。如果从火控雷达探测到的编队中选择的预定目标a1没有被末制导雷达探测到,尽管B中存在距离a1最近的点,但该点在A中与之最近的那个点却并非a1,因此a1不会出现在对应点结果中。 为了考察本文预定目标选择方法的抗干扰能力,并与以往的基于编队相互位置关系的预定目标选择方法进行比较,在Matlab 下进行了仿真实验。 由于探测概率小于1、虚警概率大于0都是和冲淡干扰一样引起两个点集元素数目的不一致,因而在仿真实验中假设探测概率为1,虚警概率为0,仅对冲淡干扰的数目进行了调整,这不影响实验的可信性。 设XOZ坐标系下真实的编队队形如图1所示,各编队中“a1”为预定目标,且让预定目标a1的坐标都统一为(100 km,0)。编队1的其余4个目标等方位间距分布在半径为R=5 km的圆周上,θ=35 °。编队2 构成人字形编队,编队中相邻目标的间距为5 km。编队3 构成菱形编队,编队中相邻目标的间距也为5 km,a1和a3距离也为5 km。用阿拉伯数字对每个编队目标编号。这些编队位置数据称为原始数据,每次仿真实验的火控数据A和末制导雷达数据B都以这些原始数据为基础产生。 A是在原始数据的基础上增加了m个干扰(每个干扰产生在随机的一个目标附近,方位随机均匀分布,且干扰离此随机目标平均距离为1.2 km,高斯均方差为0.2 km)。此外,A 还相对原始数据平移了(1.2 km,1.3 km),旋转了1°,并通过叠加火控雷达在X和Z方向上的高斯定位误差(均方差分别为0.2 km、0.6 km)来模拟形状的扭曲。 B是在原始数据的基础上受到了严重的冲淡干扰,n个目标(编号随机等概率)按照90°的方位间隔各自释放4个冲淡干扰(实际方位为正态分布随机数,均值为瞄准方位,均方差为5°),冲淡干扰的发射距离为高斯分布,均值为1.2 km,均方差为0.2 km,且各个冲淡发射互不相关。此外B相对原始数据在X和Z方向上的平移量是不相关的零均值高斯形式,均方差分别为5 km、4.6 km,以此来模拟自控段的导航误差。另外,且B相对A 旋转了4°。考虑到末制导雷达在X和Z方向上有高斯定位误差,且编队的不一致运动也会造成形状扭曲,一并通过叠加高斯误差(均方差分别为0.02 km、0.5 km)来模拟形状的扭曲。 对m、n的多个取值组合各进行了200次蒙特卡洛实验,并统计预定目标选择概率。 本文所提出的预定目标选择方法对编队1的某一次实验所用的仿真数据及其处理过程的数据状态如图2所示(非零阿拉伯数字代表了该位置目标在原始仿真数据中的编号,“0”表示干扰,m=2,n=2)。 图2 试验产生仿真数据及其处理过程的数据状态 图2中,c)为粗匹配的结果,可见通过粗匹配剔除了部分干扰。图2d)为精匹配结果,可见经过精匹配进一步剔除了一些干扰。图2e)为双向最近邻准则选择到的对应点。返回的最后对应点中,尽管目标4的对应点错误地选择为一个干扰,这个错误选择的后果也不至于完全使导弹攻击任务失败。因为这个干扰离目标4 很近,将此干扰的位置作为后续制导的测量仍可以引导导弹飞向目标位置附近,可以通过后续的一些手段来重新捕获目标4。 表1给出了本文方法和基于编队相互位置关系方法的抗干扰能力。干扰不存在时,两种方法都具有很高的预定目标选择概率,但干扰存在时,本文方法明显优于基于编队相互位置关系的方法。此外,编队队形对算法性能存在影响,构成队形的舰艇数目越多,则干扰对预定目标选择概率的影响越小。由于编队3的数据点最少,因而其预定目标选择平均概率低于另外两个编队。 表1 不同干扰程度下的预定目标选择概率 本文用基于Hausdorff距离的点集匹配理论处理反舰导弹对舰艇编队中预定目标的选择问题,即用火控雷达提供编队信息作为模板,从末制导雷达获得的编队信息中寻找对应点。提出了一种基于Hausdorff距离的部分匹配新途径,能在自适应剔除干扰的影响的同时保留形状的相似部分。 仿真试验表明本文提出的方法具有较强的对抗冲淡干扰的能力,且抗干扰能力优于以往的基于编队相互位置关系的方法。 值得注意的是,当火控雷达得到的编队目标数据存在干扰时,就可能选择到一个干扰作为预定目标,这将使本文算法失去意义。在仿真试验中,假设了装定的预定目标全是真实目标。如何在干扰环境下从火控数据中选择出预定目标,涉及到火力分配和射前识别干扰等因素,这是需要进一步深化研究的课题。 [1]卢毅,姜永华.反舰导弹目标选择的一种新方法[J].航空学报,2010,31(4):778-784. [2]沈建锋.舰艇队形识别目标选择算法[J].火力与指挥控制,2010,35(9):98-100. [3]潘哲.一种反舰导弹目标选择混合算法[J].战术导弹技术,2010(3):48-52. [4]卢毅,姜永华,刘兴明,等.一种基于Hausdorff距离的反舰导弹预定目标选择方法[J].数据采集与处理,2011,26(2):146-151. [5]HUTTENLOCHER D P,KLANDERMAN G A,RUCKLIDGE W J.Comparing images using the Hausdorff distance[J].IEEE Trans.on Pattern Analysis and Machine,1993,15(9):850-863. [6]TAN H C,ZHANG Y J.Computing Eigenface from Edge Images for Face Recognition Based on Hausdorff Distance[C]//Proceedings of IEEE International Conference on Image and Graphics.2007:639-644. [7]PAUMARD J,AUBOURG E.Adjusting astronomical images using a censored Hausdorff distance[C]//Proceedings of IEEE International Conference on Image Processing.1997:232-235. [8]HAN I,YUN I D,LEE S U.Model-based object recognition using the Hausdorff distance with explicit pairing[C]//Proceedings of IEEE International Conference on Image Processing.1999:83-87. [9]RUCKLIDGE W J.Locating objects using the Hausdorff distance.In:Proceedings of IEEE International Conference on Computer Vision.1995:457-464. [10]KWON O K,SIM D G,PARK R H.New Hausdorff distances based on robust statistics for comparing images[C]//Proceedings of IEEE International Conference on Image Processing.1996:21-24. [11]HUTTENLOCHER D P,LILIEN R H,OLSON C F.View-based recognition using an eigenspace approximation to the Hausdorff measure[J].IEEE Transactions on Pattern Analysis and Machine.1999,21(9):951-955. [12]ZHANG Z,HUANG S,SHI Z.A fast strategy for image matching using Hausdorff distance[C]//Proceedings of IEEE International Conference on Robotics,Intelligent Systems and Signal Processing.2003:915-919.3 算法实现
3.1 最小NPHD
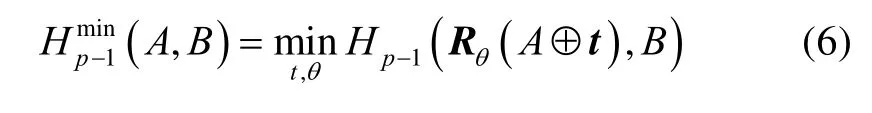
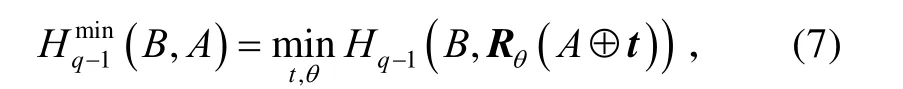
3.2 搜索最佳匹配位置

3.3 获取对应点
4 仿真试验
4.1 仿真设置
4.2 处理过程示例
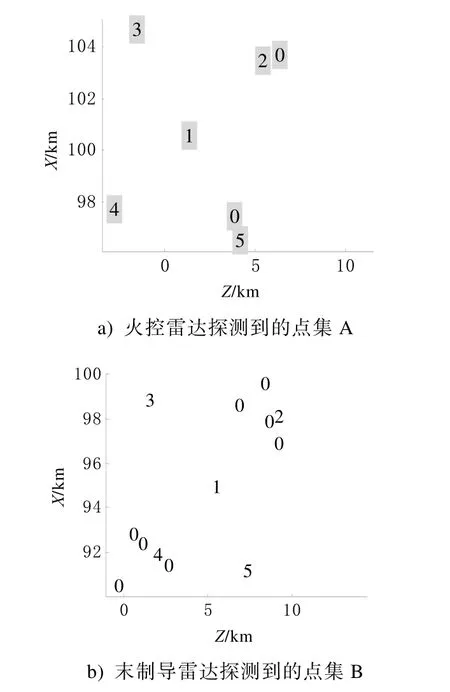
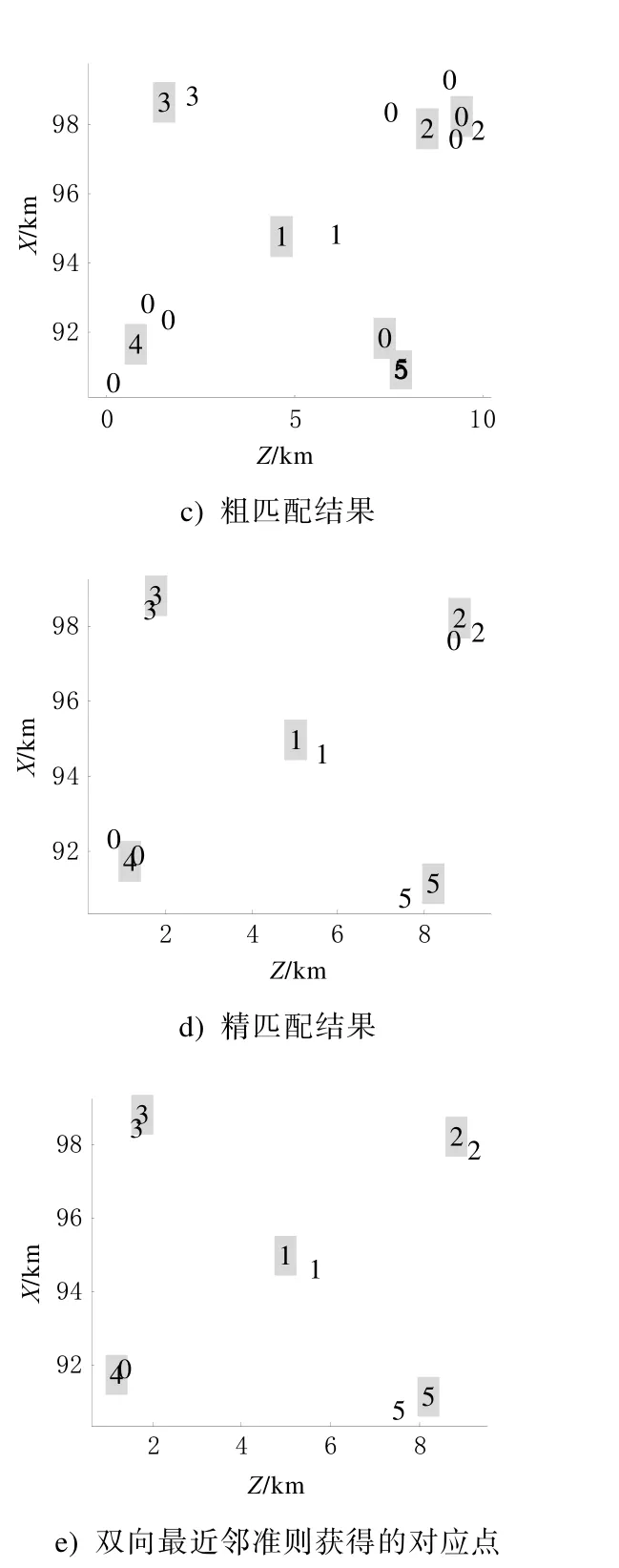
4.3 抗干扰能力
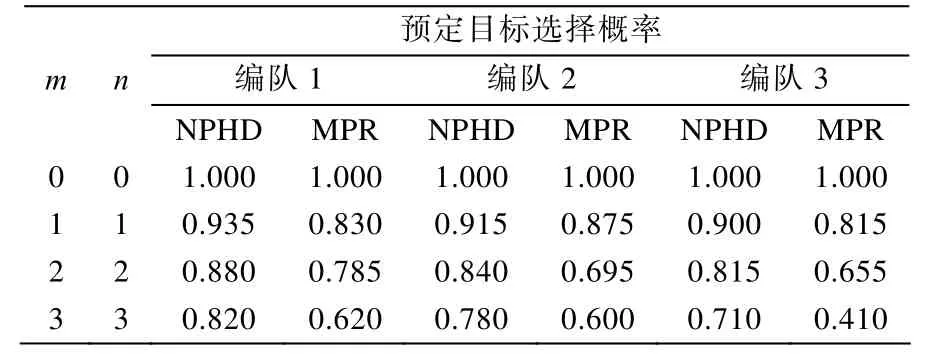
5 结论

