积空间中求解凸不等式系统的不完全投影算法
党亚峥, 高 岩
(1.河南理工大学数学与信息科学学院,焦作 454001;2.上海理工大学管理学院,上海 200093)
1 问题的提出
设Ci⊂Rn,i=1,2,…,m.Ci为欧氏空间中有限的非空闭凸集,且它们的交集非空,凸可行问题(CFP)就是求一点
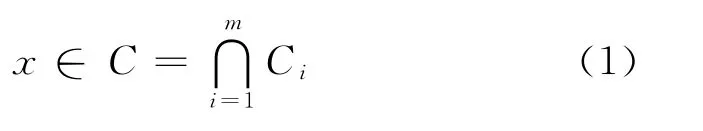
如果定义Ci={x∈Rn:fi(x)≤0} ,其中,函数fi(x)是凸的,则凸可行问题(CFP)就变成为求解不等式系统fi(x)≤0(i=1,2,…,m)的可行解的问题.
作为一类重要的复杂系统,凸可行问题在系统科学和工程技术中的应用非常广泛,如最优化[1-2]、逼近论[3-4]、图像重建的预测和计算机断层扫描[5-6]、控制理论[7-8]等.实际中很难直接找到C=中的一点,通常采用投影算法,可参见文献[9-11].投影算法产生的序列是Fejer单调的,基于这样的事实,1998年Ubaldo在文献[12]中提出了解凸可行问题的平行不完全投影算法.事实上,任何一种投影算法经过有限步迭代总能找到不完全投影点,所以,不完全投影算法包含了一般的投影算法.随后,Echebest在文献[13]中针对线性的凸可行问题提出了一种加速的不完全投影算法,但是,在这些不完全投影算法迭代步中含有权参数ωki,所以,在证明算法的收敛性时会涉及这些参数的选择问题,势必会使证明复杂化.本文利用文献[14]的思想建立一个新的积空间,转换平行的不完全投影算法为半序列的不完全投影算法,这样,一方面将求多集的交点问题转化为2个凸集的交点问题,使问题简化;另一方面使权参数隐含在一个算子中,从而更有利于简化算法的收敛性证明.
2 预备知识
现介绍文献[12]中提到的解凸可行问题的平行不完全投影算法.
算法1
步骤1 假设xk∉C,xk是当前迭代点;给定参数η,0<η≤1.
步骤2 对每个凸集Ci,i=1,2,…,m,寻找满足
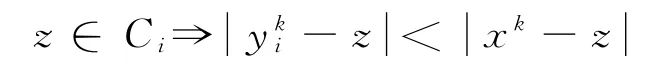
步骤4 计算
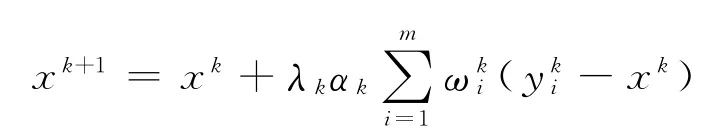
其中
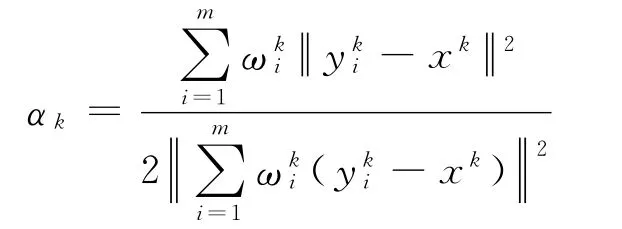
一般的投影算法产生的迭代序列是Fejer单调的,即如果序列{xk}由投影算法产生,则,所以,在算法1中,不完全投影点可以通过有限步的投影算法得到.
3 算法转换
算法1含有加速因子αk和松弛参数λk,η≤λk≤2-η,0<η≤1.因此,它是一种加速的不完全投影算法.但是,本文只考虑下松弛的情况,也就是在算法1中取αk=1,λk∈(0,1).现介绍具体过程.
3.1 下松弛的不完全投影算法
算法2
步骤1 假设xk∉C,xk是当前迭代点.
步骤2 对每个凸集Ci,i=1,2,…,m,寻找满足
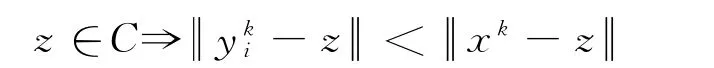
步骤4 计算
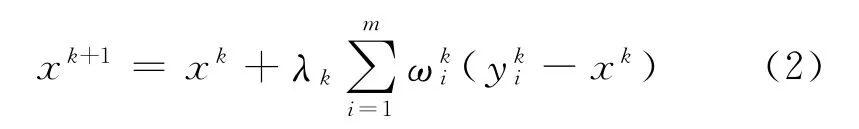
其中,λk∈(0,1).
3.2 新的积空间
为了简化算法2的收敛性证明,将平行不完全投影算法转化为半序列不完全投影算法,首先需要建立新的积空间,其定义为
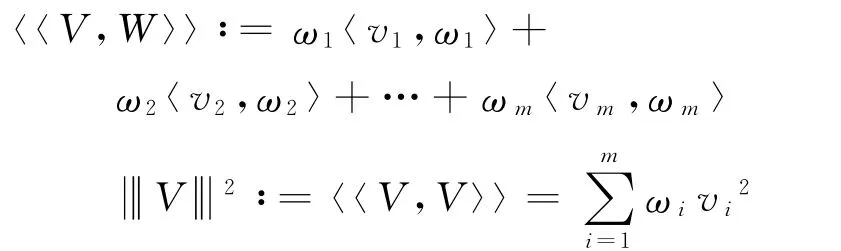
其中,V=(v1,v2,…,vm)∈(Rn)m,vi∈Rn,i=1,2,…,m,W=(w1,w2,…,wm)∈(Rn)m,wi∈Rn,i=1,2,…,m.这样就可以构建一个新的积空间和分别表示新空间的内积和范数.为了方便起见,空间可以简记为(Rn)m,为便于区别Rn中的点,这里用大写字母表示(Rn)m中的点.
现定义新的积空间(Rn)m中的两个子集.其一,定义集N∶≡C1×C2×…×Cm,即Rn中的凸集Ci的笛卡儿积,i=1,2,…,m.显然,N是空间(Rn)m中的闭集.其二,定义集D,D为Rn在常规嵌入q∶Rn→(Rn)m下的像,即对∀v∈Rn,令q(v)≡(v,v,…,v).
显然,如果C≠Ø,则N∩D≠Ø, 而且q(C)=N∩D.这样,在原始空间中找C中的一点就等价于找N∩D中的一点,并且这些点是一一对应的.因此,在子集D⊂(Rn)m中构建一个序列{Xk}收敛到N∩D中的一点,就可以在Rn中找到一个相应的序列{xk}收敛到C中相应的一点.
命题1 设V=(v1,v2,…,vm)∈(Rn)m,定义算子
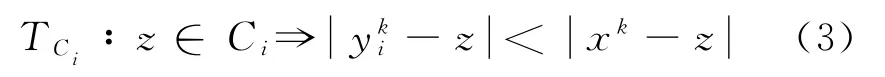
也就是自变量xk经过算子TCi运算后得到满足不等式(3)的点yki,即TCi(xk)=yki,直接定义算子
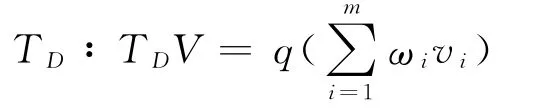
其中

则对任意Z∈D∩N,有
a.TNV=(TC1v1,TC2v2,…,TCmvm);
证明 显然,TD是线性算子.
a.由新空间的范数的定义可得
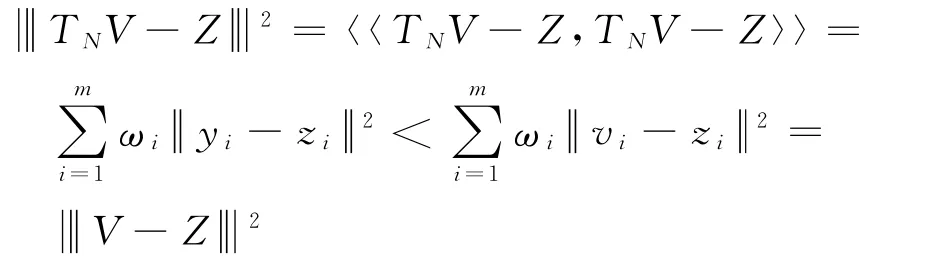
所以
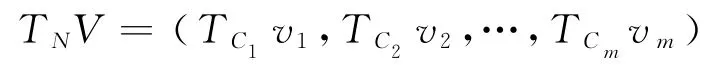
b.由TD的定义可得
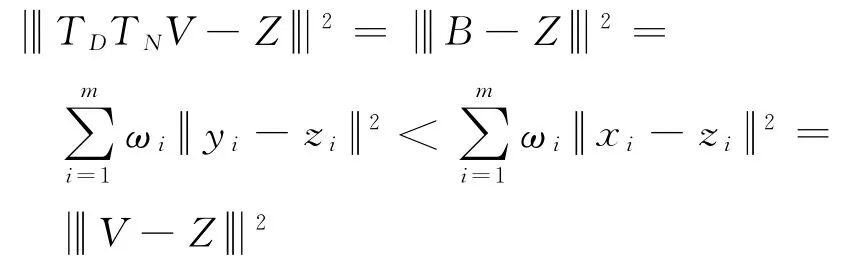
其中
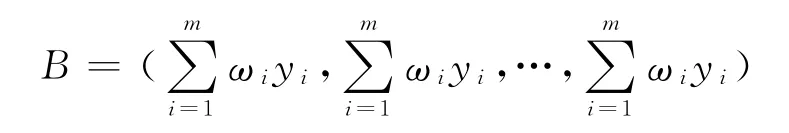
3.3 转换平行算法为半序列算法
现给出算法2对应的积空间中的半序列投影算法.
算法3
步骤1 取D中任意一点X0=q(x0).
步骤2 计算
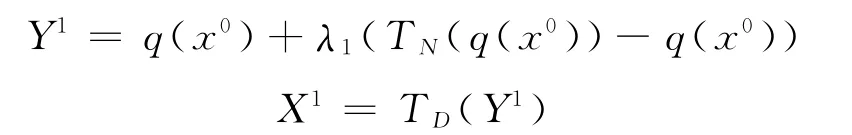
步骤3 计算
其中,λk∈(0,1).
显然,由于Xk=q(xk),以上下松弛不完全投影算法产生的序列{Xk}⊂D,对应Rn中的序列{xk}.
命题2 假设Z∈D∩N,则
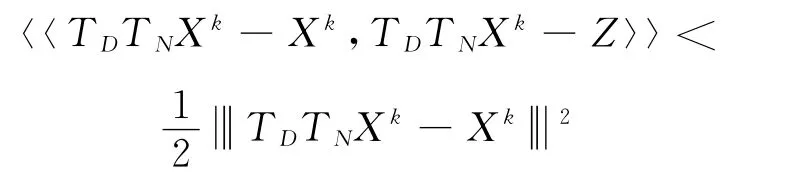
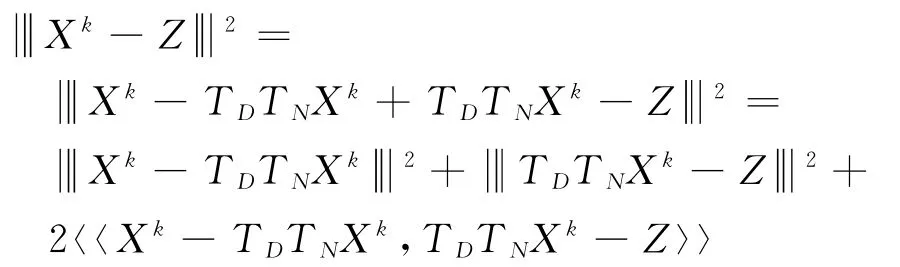
证明
由命题1得
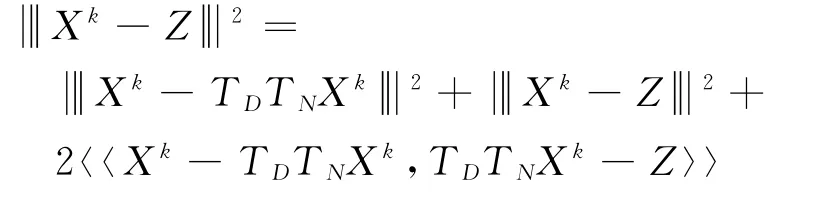
因此
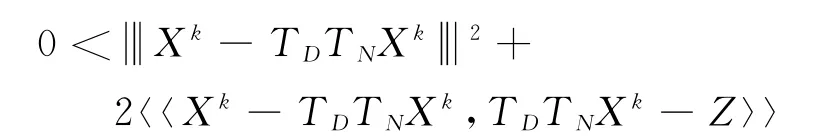
显然,可以直接得出结果.
推论1 令Z∈D∩N,则
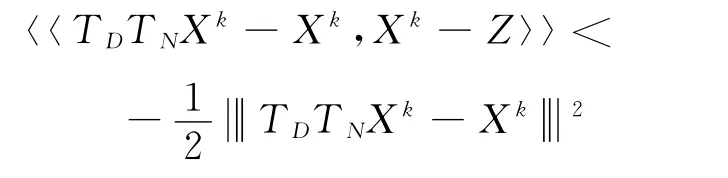
证明 由命题2很容易得到
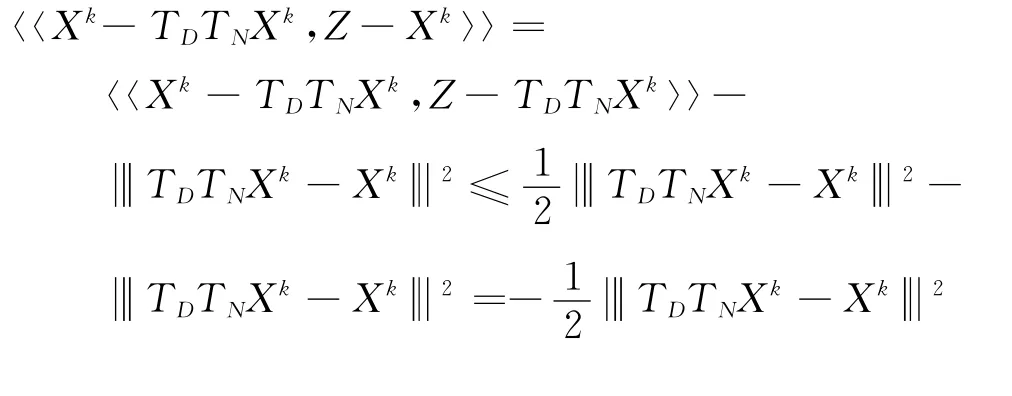
4 收敛性证明
首先证明积空间中算法3的收敛性,然后基于算法2与算法3的等价性给出算法2的收敛性定理和相应的简单化证明.
定理1 令Z∈D∩N,则
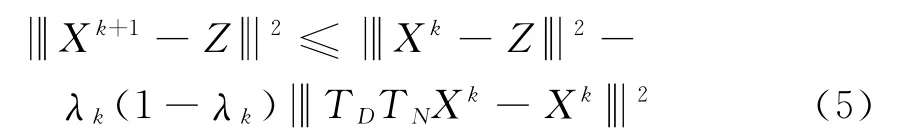
证明 由式(4)得
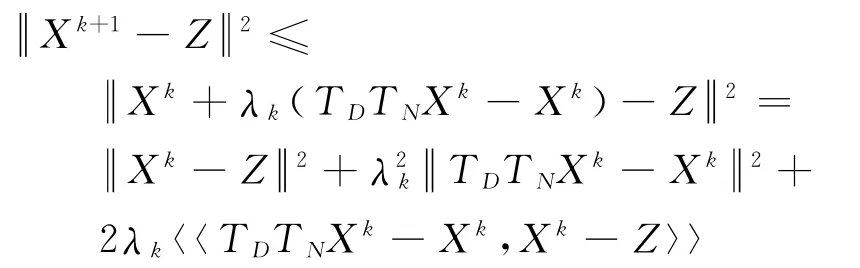
由推论1可知
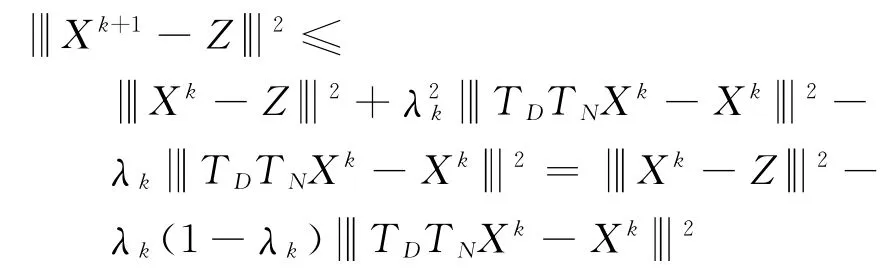
故定理1得证.
假设
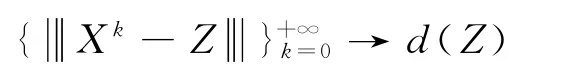
显然
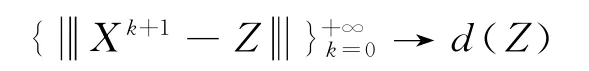
再由式(5)可得

另外,由式(5)得
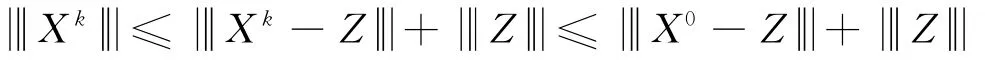
定理2 如果D∩N≠Ø,任取D中的点X0为起始点,则由算法3产生的序列收敛于点D∩N中的一点,记为Z.
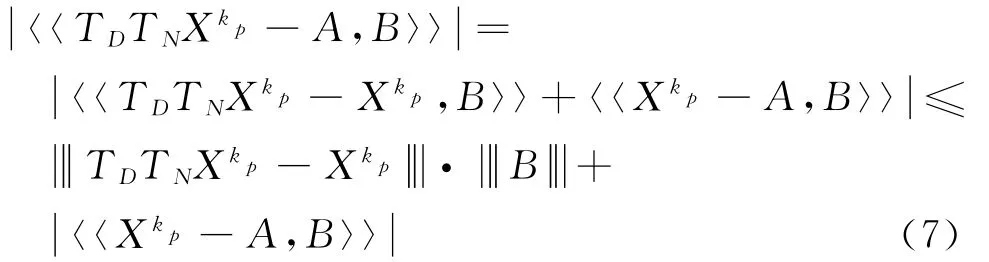
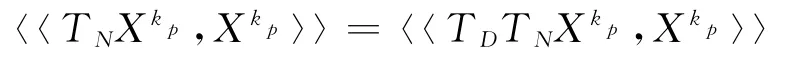
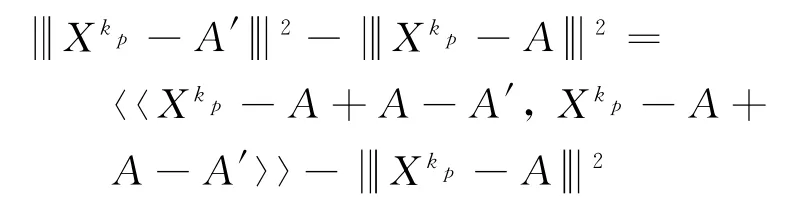
经过内积运算,得
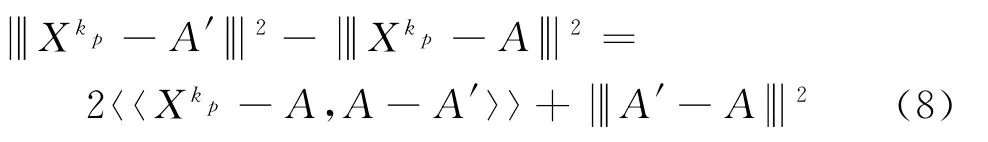
同理.对任意p′∈Z+,有
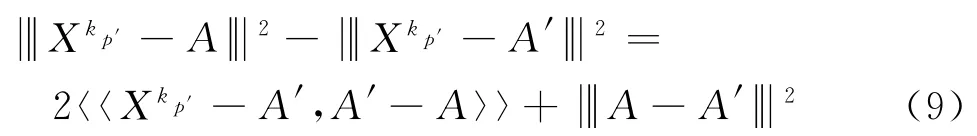
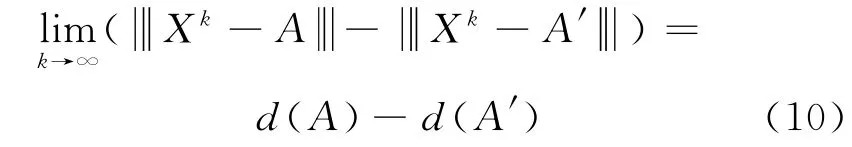
对p→∞和p′→∞,式(8)和式(9)分别取极限,可得
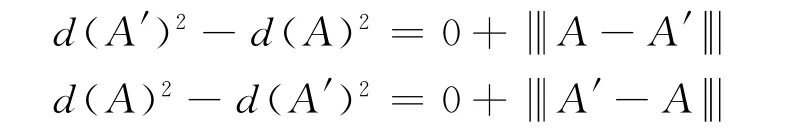
故A′=A.所以,定理2得证.
将平行不完全投影算法转换为半序列不完全投影算法的主要优点是能够通过序列的收敛性质得到相应的序列的收敛性质.基于此,给出定理3.
定理3 当(Rn)m中的序列收敛于一点A∈D∩N时,则在空间Rn中其相应的序列也收敛到一点a∈C,并且a=q(a).
对任意b∈Rn,取一个指标j∈{1,2,…,m},有
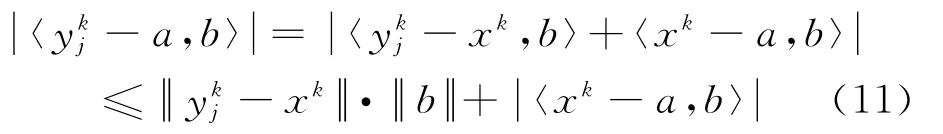
由式(7)可以得到不等式(11)右边的第一项趋向于0,由于序列收敛到一点a,显然,第二项也趋于0.所以,又由于Cj.所以
5 结 论
原空间的平行不完全投影算法转换为一个新空间中的半序列不完全投影算法,这样,平行不完全投影算法的收敛性就可以由半序列不完全投影算法的收敛性得到,在某种程度上简化了平行不完全投影算法的收敛性证明.
但是,本文只是下松弛的平行不完全投影算法,是否能拓展到上松弛和加速的情况仍然是有待解决的问题.
[1] Chinneck J W.The constraint consensus method for finding approximately feasible points in nonlinear programs[J].Informs J Comput,2004,16(3):255-265.
[2] Censor Y,Lent A.Cyclic subgradient projections[J].Math Program,1982,24(1):233-235.
[3] Deutsch F.Best approximation in inner product space[M].New York:Springer-Verlag,2001.
[4] Deutsch F.The Method of alternating orthogonal projections,approximation theory,spline functions and applications[M].Dordrecht:Kluwer Academic Publishers,1992,105-121.
[5] Censor Y.Parallel application of block iterative methods in medical imaging and radiation therapy[J].Math Program,1998,12(2):307-325.
[6] Gould N I M.How good are projection methods for convex feasibility problems[J].Comput Optim Appl,2008,40(1):1-12.
[7] Boyd S,EI Ghaoui L,Feron E,et al.Linear matrix inequalities in system and control theory[M].Philadlphia:Society for Industrial and Applied Mathematics,1994.
[8] 高岩.仿射非线性控制系统生存性的判别[J].控制理论与应用,2009,29(6):654-656.
[9] Baushke H H,Borwein J M.On projection algorithms for solving convex feasibility problems[J].SIAM Rev,1996,8(3):367-426.
[10] Eremin I I.On systems of inequalities with convex functions in the left-hand sides[J].Amer Math Soc Trans,1970,88(2):67-83.
[11] Herman G T.Image reconstruction from projections:the fundamentals of computerized tomography[M].New York:Academic Press,1980.
[12] Garcia U M,Gonzalez F J.Icomplete projection algorithms for solving the convex feasibility problem[J].Numer Algorithms,1998,18(2):177-193.
[13] Echebest N,Guradarcci M T.An acceleration scheme for solving convex feasibility problems using incomplete projection algorithm[J].Numerical Algorithms,2004,35(2/3/4):331-350.
[14] Crombez G.Viewing parallel projection methods as sequential ones in convex feasibility problems[J].Trans Amer Math Soc,1995,347(7):2575-2583.

