一种改进的模糊C-均值聚类算法
曹 易, 张 宁
(上海理工大学管理学院,上海 200093)
聚类是根据对象之间的相似性来将他们聚集成不同类别的方法.评价一个聚类质量的好坏,总体是该聚类结果中同一类内部的对象尽可能相似,不同类之间的对象尽可能相异.到目前为止,数据挖掘中常用的聚类算法有层次聚类、划分聚类、基于网格聚类、基于密度聚类及模糊聚类等[1].
传统的聚类是一种硬性划分,具有“非此即彼”性,但是,现实生活中很多事物是“亦此亦彼”,很难将它们严格地划分到一个具体的类中.模糊C-均值聚类算法(FCM)是应用最广泛的聚类算法之一[2],它具有算法简单、收敛速度快、能处理大规模数据等优点,因此,该算法已经有效地应用在数据挖掘、模式识别及决策支持等领域,具有很大的理论以及实践价值.但是,FCM算法同时也存在着很大的局限性[3]:聚类数与聚类初始中心的选择极大地影响着聚类效果,并且该算法采用梯度法求解极值,所求解往往是局部最优.为此,文献[4]用信息熵来计算最佳聚类数目,Yager和Filev[5]提出了一种称为爬山法的初始聚类中心方法.
由于一般模糊C-均值算法的上述缺点,本文提出了一种改进的FCM算法.首先用概率密度的思想得到最佳聚类数和初始聚类中心,其次通过对拥有次大隶属度的中心点加入一个抑制因子来加速算法收敛,最后用一个兼顾类内距与类间距的新的目标函数来替代原有的目标函数.经实验证实,该算法在聚类结果质量与算法速度上都有了一定程度的改进.
1 普通模糊C-均值的算法
设X={x1,x2,…,xn}是待聚类的对象的全体(论域),X中每个对象(样本)xk(k=1,2,…,n)可以用有限个参数值来描述,每个参数刻画xkj的某个特征.所以,对象xk就可以用一个向量P(xk)=(xk1,xk2,…,xks)来表示,P(xk)为xk的特征向量[6].uik表示X中第k个对象对第i类的隶属度函数,vi(i=1,2,…,c)表示聚类中心,则第k个对象到第i个聚类中心vi的欧式距离为
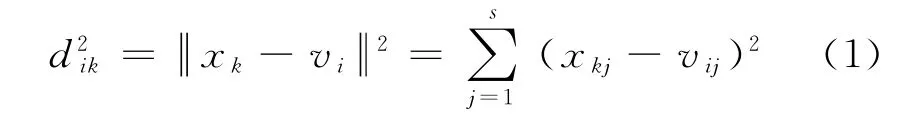
目标函数定义为
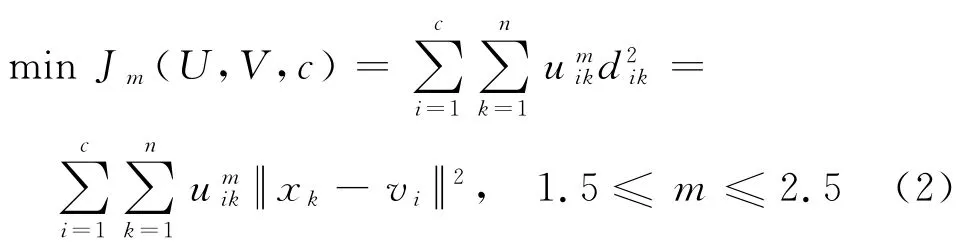
随着隶属函数uik和中心点vi不断更新,若目标函数Jm(U,V,c)达到了满意的稳定程度,就终止迭代算法.
2 改进的模糊C-均值的算法及其实现
2.1 聚类数和初始聚类中心选取的改进
上述算法具有简单、收敛速度快、能处理大规模数据等优点,但是,聚类数和聚类初始中心的选择极大地影响着聚类效果,并且该算法采用梯度法求解极值,所求解往往是局部最优.
目前,在FCM算法中,聚类数和初始中心点的选择对算法的复杂度以及聚类效果的影响相当大,因此,选择一个适合的中心点是至关重要的.本文利用一种概率密度函数来选择聚类数和初始中心[9,10].定义对象xi处的密度函数为
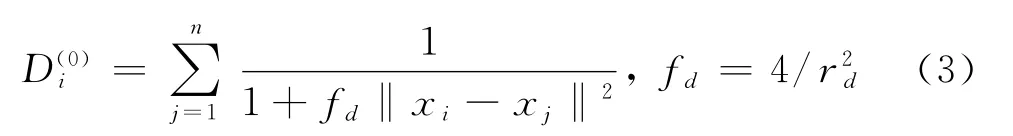
其中,rd为邻域半径,其数值与数据的分布特性有关.
本文取rd为n个对象的平均距离,即
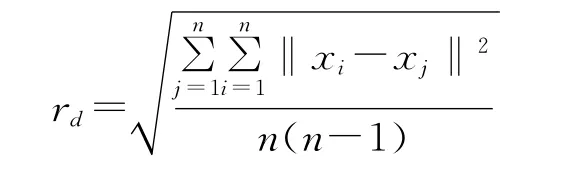
显然,xi周围分布越密集,rd值越小,密度函数值越大.令其满足条件的点取为第一个初始聚类中心,设为x*1.第k个聚类中心点为
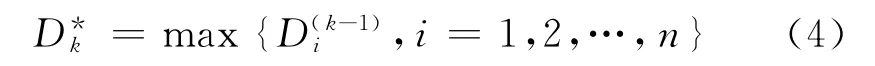
第k次迭代时的聚类中心的密度函数为
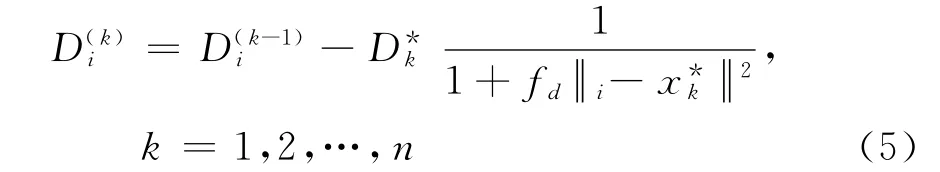
2.2 隶属度的改进
由FCM算法可知,聚类实际上就是一个隶属矩阵u和聚类中心v交替优化过程.可以修正隶属矩阵u来计算下一次迭代的聚类中心v,使计算结果更合理,提高算法的收敛速度.隶属度越大,样本点对类中心的吸引力就越大,类中心的下一次迭代值受隶属度的影响就越大[11].本文根据竞争学习算法,给出了一种修正隶属矩阵u的算法.本文称距离样本点最近的类中心为赢者,距离次近的为赢者对手,通过减弱对手的吸引力来加快赢者的收敛速度.加入一个抑制因子α∈[0,1],抑制次近样本点的吸引力,来加快算法收敛速度.具体描述为:对于对象xj,假如它对第t类的隶属度最大,为utj;对第s类的隶属度次大,为usj.给定抑制因子α,根据式(6)修改隶属度为
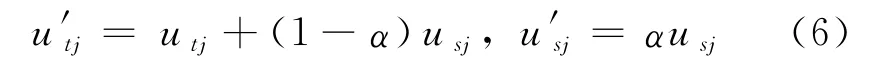
其余对象的隶属度不变.
2.3 目标函数选取的改进
聚类结果应该是类内尽可能紧凑,类间尽可能疏远.但是,传统的FCM算法的目标函数只考虑了类内距离,没有重视类间距离.本文根据Xie-Beni提出的聚类有效性指标[12],给出一种兼顾类内和类间距离的有效性指标,将它作为新的目标函数.
类内差异W(u,v,c)和类间差异B(u,v,c)分别为
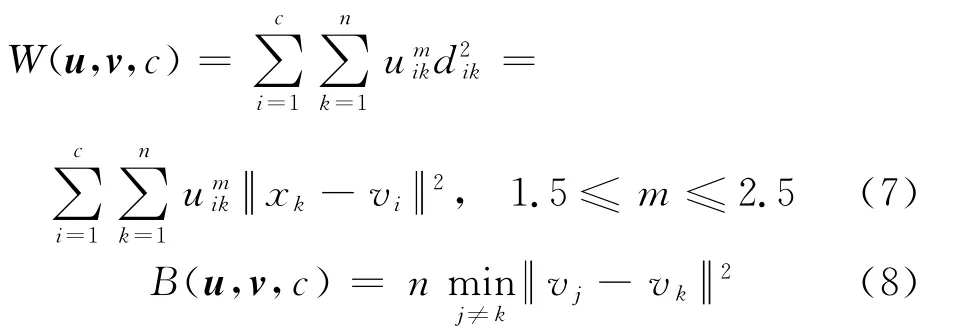
将W(u,v,c)和B(u,v,c)的商作为新的目标函数Jm(u,v,c),即
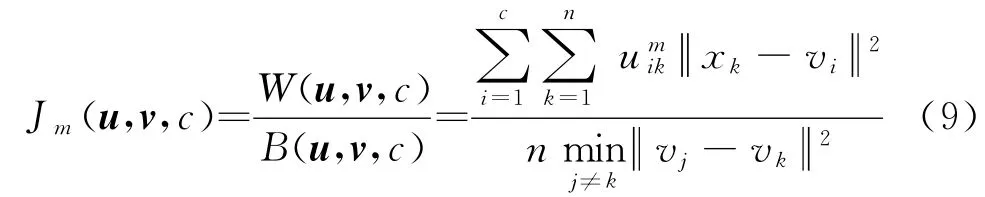
2.4 模糊C-均值算法改进的具体实现
综上所述,现给出该算法的具体步骤.
Step 1 给定待聚类对象集X,参数δ,模糊因子m,抑制因子α,迭代参数ε.
Step 2 根据式(3)~(5)求出初始聚类数c和聚类中心v.
Step 3 计算隶属矩阵uik,再根据式(6)修改u.
Step 4 更新聚类中心vi.
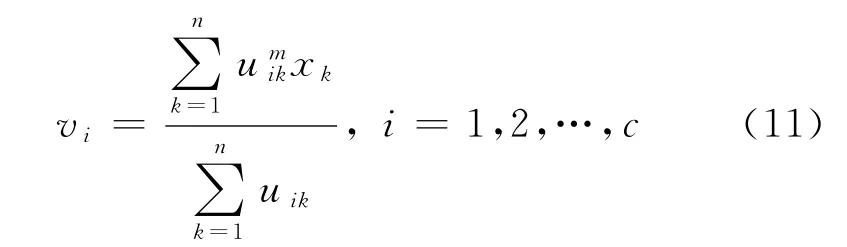
Step 5 根据式(9)计算Jm(u,v,c),若式(12)成立,终止计算;否则,l=l+1,转向Step 3.
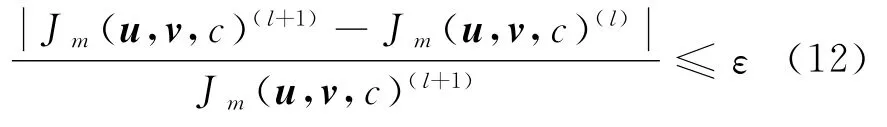
3 实验结果及分析
通过实验来测试改进算法的效率和聚类质量,并与普通的模糊C-均值算法进行比较.本次实验平台操作系统为Windows XP,CPU为双核E7500 2.9GHz,内存2GB.数据采用某高校的Web访问日志,共有2 993个IP用户,访问的网页被综合成了教育、娱乐、搜索等35个类别,每个类别认为是用户的一个属性值,大小取该用户对该类别的访问频率,得到了2 993×35的用户类别矩阵.实验取模糊因子m值为2,最大可能迭代次数为200,通过改变参数δ,α和ε的值来测试算法的性能,得到参数的最佳取值范围.聚类结果的有效性指标p[13]用式(13)来评价,值越小,则聚类效果越好;反之亦然.N为算法迭代次数.
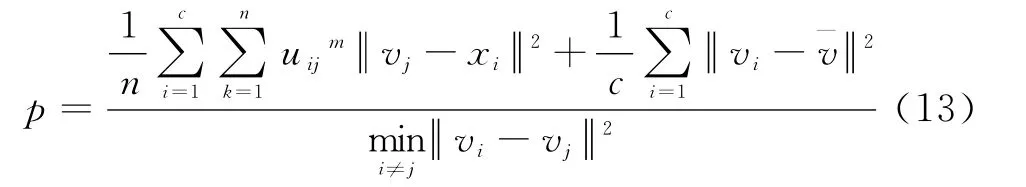
经调整实验控制参数得出结果如图1~4所示.
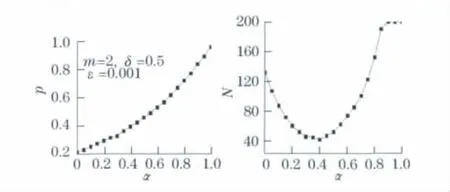
图1 聚类有效性p和迭代次数N与α的关系Fig.1 Relationship of clustering validity p,iteration number Nandα
从图1~4可以看出:
a.当m=2,δ=0.5,ε=0.001时,随着参数α从0变化到1时,有效性指标p与迭代次数N的变化趋势如图1,综合考虑该算法的聚类质量以及迭代次数,取α=0.3较为合理.
b.在图2中,当m=2,α=0.3,ε=0.001时,随着参数δ从0变化到1时,有效性指标p,迭代次数N以及聚类数c变化趋势如图2(见下页),同样综合考虑该算法,取δ=0.5较为合理,此时聚类数c=43.
c.当m=2,α=0.3,δ=0.5时,随着参数ε从0.000 5~0.001 4之间变化时,有效性指标p与迭代次数N的变化趋势如图3(见下页),同样综合考虑该算法,取ε=0.001较为合理.
d.取m=2,α=0.3,δ=0.5,ε=0.001时,用本文的改进FCM算法与经典的FCM算法进行比较,从图4(见下页)中可以看出,当聚类数目相同时,与经典FCM算法相比,本文算法在有效性指标p与迭代次数N上均有一定程度的提高.
综上所述,本文提出的改进FCM算法中,通过调节参数α,δ,ε的大小,其中本文的数据中α=0.3、δ=0.5、ε=0.001,较原有的FCM算法在聚类质量和算法速度有一定程度的提高.
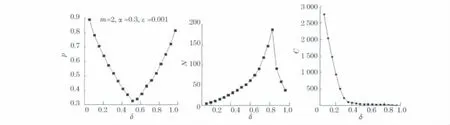
图2 聚类有效性p,迭代次数N及聚类数c与δ的关系Fig.2 Relationship of clustering validity p,iteration number N,cluster number c andα
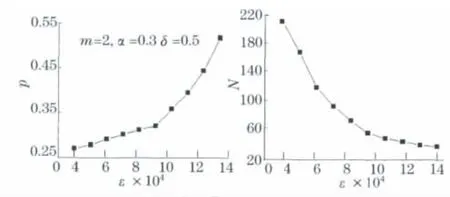
图3 聚类有效性p和迭代次数N与ε的关系Fig.3 Relationship of clustering validity p,iteration number Nandε
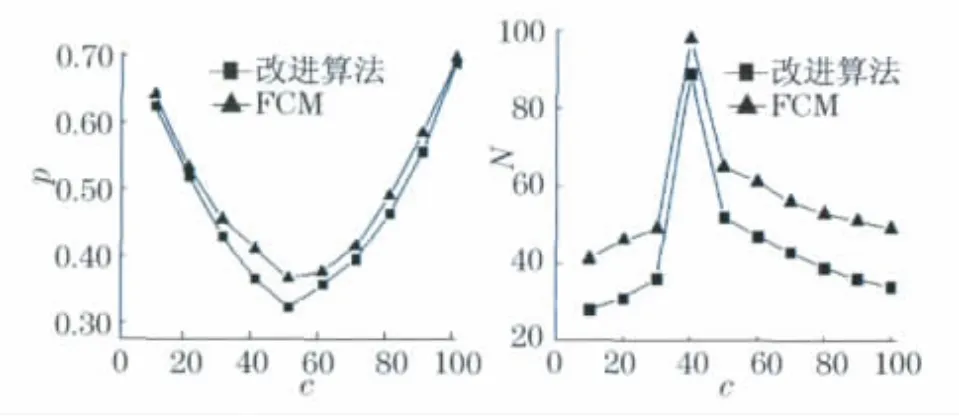
图4 改进的FCM算法与经典FCM算法比较Fig.4 Comparison of the improved FCM and classical FCM algorithm
4 结 论
通过分析经典的FCM算法中的局限性,例如聚类结果对聚类数和初始聚类中心的敏感性,以及目标函数选取只考虑类内部距离而忽略了类间距离,提出了一种改进的FCM算法.经实验证明,与经典算法相比,改进算法不论是在聚类质量上还是在算法复杂度上,都有一定程度的提高.用概率密度函数找到最佳的聚类数以及初始聚类中心点;利用竞争学习算法中的抑制对手来修改隶属矩阵,从而达到加快算法的收敛速度;用一个类内距离与类间距离兼顾的新目标函数替换原有目标函数.实验证明,本文算法在参数设置合理的情况下,聚类质量和算法速度在原有FCM算法上有一定程度的提高.
[1] Mitra S,Pal S K,Mitra P.Data mining in soft computing framework:a survey[J].IEEE Transactions on Neural Networks,2002,13(1):3-14.
[2] 贺玲,吴玲达,蔡益朝.数据挖掘中的聚类算法综述.计算机应用研究,2007,1(1):16-19.
[3] 齐淼,张化祥.改进的模糊C-均值聚类算法研究.计算机工程与应用,2009,45(20):133-135.
[4] 沈红斌,杨杰,王士同,等.基于信息理论的合作聚类算法研究[J].计算机学报,2005,28(8):1287-1294.
[5] Yager R R,Filev D P.Approximate clustering via the mountain method[J].IEEE Transactions on SMC,1994,24(8):1279-1284.
[6] 张敏,于剑.基于划分的模糊聚类算法[J].软件学报,2004,15(6):858-868.
[7] 朱文婕,吴楠,胡学钢.一个改进的模糊聚类有效性指标[J].计算机工程与应用2011,47(5):206-209.
[8] 高新波,裴继红,谢维信.模糊C-均值聚类算法中的加权指数m的研究[J].电子学报,2000,28(4):80-83.
[9] 饶泓,扶名福,谢明详.基于模糊聚类的神经网络故障诊断方法[J].微计算机信息,2007,1(1):196-197.
[10] 李春生,王耀南.聚类中心初始化的新方法[J].控制理论与应用,2010,27(10):1435-1440.
[11] 张曙红,孙建勋,诸克军.基于遗传优化的采样模糊C-均值聚类算法[J].系统工程理论与实践,2004,5(1):121-125.
[12] Xie X L,Beni G.A validity measure for fuzzy clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1991,13(8):841-847.
[13] Kwon S H.Cluster Validity index of fuzzy clustering[J].Electronics Letters,1998,34(22):2176-2177.

