级数突变理论在贸易竞争力评价中的应用

于开红

（重庆三峡学院 经济与管理学院，重庆 万州 404100）

0 引言

我国高技术产业具有外向度高和出口导向明显的特征，在2008～2010年，中国高技术产业出口交货值占国家货物出口总值比率的平均值为33.97%（原始数据来自2011年《中国高技术产业统计年鉴》）。根据国家发展与改革委员会提供的数据，2011年中国高新技术产品出口规模已达到5488亿美元，占全国外贸出口的39%，居世界第1位。对中国高技术产业贸易竞争力进行科学评价，并深入剖析其中制约因素，进而提升我国高技术产业贸易竞争力，促进经济更好更快发展，就显得尤为重要。基于此，文章运用级数突变理论对中国高技术产业贸易竞争力进行了系统评价，剖析其中主要影响因素，并给出了改进的对策与建议。

1 突变级数法理论

法国数学家R.Thom（1972）创立了突变理论，该理论是由结构稳定的拓扑理论发展起来的，是建立在拓扑动力学、微积分、奇点理论等数学理论基础上的新兴数学理论研究分支，专注于不连续变化现象的研究，被誉为“微积分学以后的一次数学革命”。该理论是通过势函数对研究系统的临界点进行分类，在此基础上对研究临界点附近非连续性态的特征进行研究，最终得出初等突变模型，为进一步深入探索自然和社会中突变现象奠定基础。

突变级数法是在突变理论基础上发展起来的，其突出优点是无需对评价指标赋予权重，但是需要对各项指标的相对重要性进行排序，这一方法减少了人为主观性在评价中的不当干预，是一种科学的、合理的、计算简单的评价方法。这一方法首先对评价目标进行多层次矛盾分解，再基于模糊数学理论和突变理论得出突变模糊隶属函数，通过归一化公式进行综合量化计算求出总隶属函数，归一为一个统一参数，进而得出目标的综合评价结果。

1.1 突变级数模型类型

在对目标进行综合评价时，首先要依据主次关系对评价指标体系进行矛盾分解，由于一般突变系数任意状态变量的控制变量不能超过四个，所以各级指标分解数目就不能超过四个。最重要将分解结果排列成倒树状结构，原始数据只需采集最低层级指标的数据。

突变级数模型总共有7个，其中最为常用的为3个，分别是尖点突变级数模型、燕尾突变级数模型和蝴蝶突变级数模型，详细内容见表1。其中，f(x)表示系统中某一状态变量x的势函数，而a、b、c、d则表示该状态变量的控制变量。势函数的状态变量和控制变量是相互矛盾的，但是各个控制变量之间是相互作用的，具体排列的时候要将主要控制变量置于次要控制变量之前。在选择突变级数模型时，如果一个指标可以分解为2个子指标，则采用尖点突变级数模型；如果一个指标被分解为3个子指标，则采用燕尾突变级数模型；如果一个指标被分解为4个子指标，则采用蝴蝶突变级数模型。

1.2 突变级数模型归一化公式

利用突变级数模型对案例进行综合评价的过程，亦即基于模型归一化公式将案例各级指标体系逐级向上归一化的过程，最终得出一个综合评价指标。模型归一化公式形式对评价结果有重要影响，文章接下来以尖点突变级数模型为例，对归一化公式进行推导。

对尖点突变级数模型求一阶导数，且令 f'(x)=∂f(x) /∂x=0，则 f(x)所有临界点构成的平衡曲面方程为：

再对平衡曲面方程求一阶导数，并令其等于0，即令

f''(x)=∂f'(x)/∂x=0，则得：

联立式（1）和式（2），消去x，则得到分歧方程：

求解上述分歧方程得：

其中，xa表示控制变量为a时x的状态，xb表示控制变量为b时x的状态。为了计算的方便，实践中通常把状态变量和控制变量都控制在[0，1]区间内。

当xa=1时，a=-6，若将a控制在[0，1]区间内，则需将a缩小-6倍，可令a'=a/-6，则有：

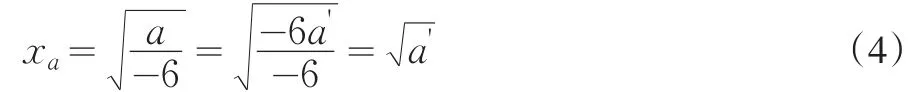
综上，得出尖点突变级数模型的归化一化公式：

同理，可以推导得出燕尾突变级数模型和蝴蝶突变级数模型的归一化公式，推导结果如表1所示。

1.3 级数突变模型归一化原则

在基于突变级数模型进行多目标评价过程中，需要遵循两个基本原则，即互补原则和非互补原则。如果一个系统中的各个控制变量不能相互替代，亦即不能相互弥补彼此的不足，就表明这些控制变量间不存在明显的相互关联作用，此时则需要基于非互补原则，实施“大中取小”进行归一化，即从各控制变量中选取取值最小的一个值。如果一个系统中各个控制变量能够相互替代，亦即能够弥补彼此的不足，就表明这些控制变量间存在明显的相互关联关系，则此时需要基于互补原则，实施“取均值”进行归一化，即取所有控制变量的平均值。

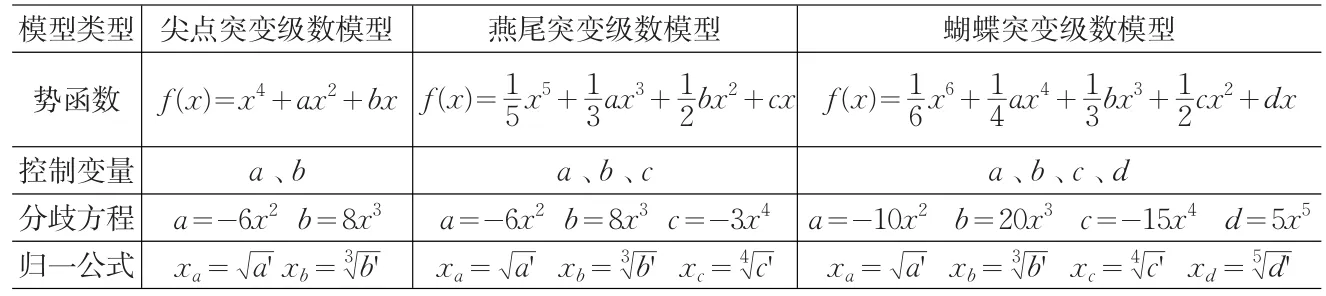
表1 突变级数模型势函数、分歧方程、归一化公式一览表

2 指标体系构建与数据来源

为对高技术产业贸易竞争力评价进行科学地、系统地、全方位地评价，并基于数据可得原则，本文共设计了4个二级指标体和14个三级评价指标，见表2。

本文选取2010年高技术产业中的14个行业作为研究对象，对其贸易竞争力进行综合评价，所使用原始数据均来自《中国高技术产业统计年鉴2011》。

表2 高技术产业贸易竞争力评价指标体系

3 实证研究

3.1 原始数据标准化

原始数据取值范围和度量单位差异较大时，会导致评价结果缺少科学性和可比性，所以基于级数突变模型进行归一化计算要求预先对数据进行标准化处理，将控制变量数据控制在[0,1]范围内。文章采用如下公式对原始数据进行标准化处理。

在式（7）中，i=1,2,…,m（m为指标数），j=1,2,…,n（n为指标数），原始数据经过上述处理便得到了标准化数据。

3.2 贸易竞争力评价推演

基于级数突变模型对中国高技术产业贸易竞争力进行综合评价，亦即对其评价指标体系逐级向上归一化，文章接下来以化学药品制造业（MCM）为例，演示归一化评价过程。

（1）MCM行业规模因子（X1）计算

X11、X12、X13适用于尖点突变级数模型，归一化公式为：

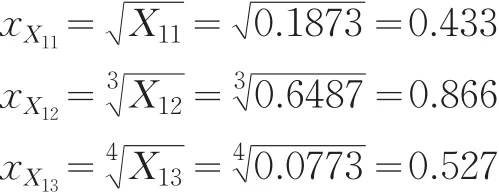
依据互补原则得行业规模因子值：

（2）MCM技术强度因子（X2）计算

X21、X22、X23、X24适用于燕尾突变级数模型，归一化公式为：

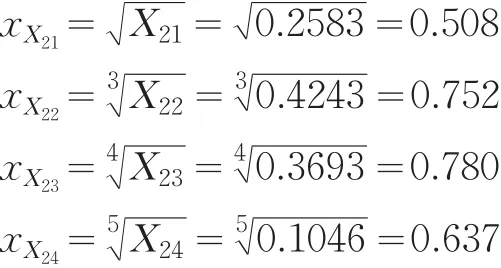
依据互补原则得行业规模因子值：

（3）MCM开放强度因子（X3）计算

X31、X32、X33、X34适用于燕尾突变级数模型，归一化公式为：

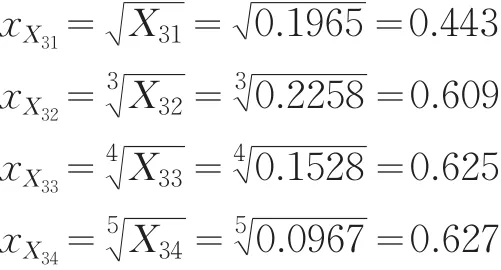
依据互补原则得行业规模因子值：

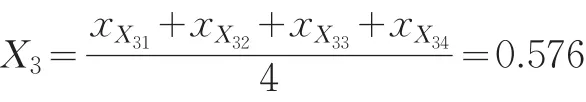
（3）MCM市场绩效因子（X4）计算

X41、X42、X43适用于尖点突变级数模型，归一化公式为：

依据互补原则得行业规模因子值：

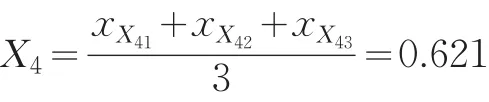
（4）MCM综合因子（Comp（MCM））计算

X1、X2、X3、X4燕尾突变级数模型，归一化公式为：

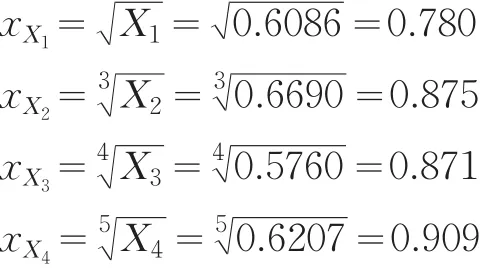
依据互补原则得综合因子值：

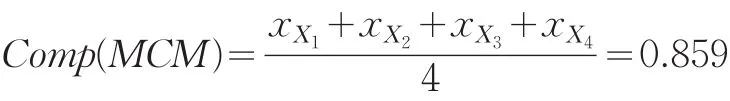
依据同样方法，可计算得出CHM、CHM、MBBC、MRA、MCE、MBTE、MEA、MEC、TVRR、OEE、MEC、MCPE、MOE、MMEA、MMI综合因子得分值，详细计算结果请参阅表4.1。其中，MCM、CHM、MBBC分别代表医药制造业中的化学药品制造业、中成药制造业和生物生化制品制造业3个子产业。MRA代表航空航天制造业中的飞机制造及修理产业。MCE、MBTE、MEA、MEC、TVRR、OEE分别代表电子及通信设备制造业中的通信设备制造业、广播电视设备制造业、电子器件制造业、电子元件制造业、家用视听设备制造业、其他电子设备制造业。MEC、MCPE、MOE代表电子计算机及办公设备制造业中的电子计算机整体制造业、电子计算机外部设备制造业、办公设备制造业。

4 研究结论和政策启示

表3列示了高技术产业行业规模、技术强度、开放强度、市场绩效4个综合因子得分情况，以及其综合贸易竞争力得分情况。表4列示了高技术产业贸易竞争力分级情况。综合两表信息，发现MEC、MEA、MCE、MCPE产业贸易竞争力处于A级，得分居于0.900以上，且其行业规模、技术强度、开放强度、市场绩效4个综合因子得分整体上也居于前4地位（虽然市场绩效因子得分偶有意外）。MEC、MCM、TVRR、MMI、OEE、CHM、MMEA、MRA、MBBC产业贸易竞争力处于B级，综合贸易竞争力得分居于0.700～0.899之间，影响其贸易竞争力水平的4项综合因子得分水平虽有小幅震动，但整体上限于5～13排位间。MBTE、MOE贸易竞争力水平最低，等分分别为0.601和0.497，别列入C等级，影响其贸易竞争力水平的4个综合因子得分也处于最低水平。

表3 高技术产业贸易竞争力评价得分及排名

表4 高技术企业贸易竞争力分类

为进一步深入考察高技术产业贸易竞争力及其影响因子在各产业间的差距，依据表4.1绘制柱状图1。贸易竞争力处于A级的产业中，行业规模和市场绩效优势明显，对贸易竞争力提升发挥了最为重要的作用。技术强度对MCE贸易竞争力提升贡献突出，开放度对MEC、MEA贸易竞争力贡献也比较显著。对于贸易竞争力处于B级的高技术产业而言，行业规模和技术强度对贸易竞争力提升贡献更为突出。对于C级的MBTE、MOE两个产业而言，其4个综合影响因子贡献均不显著。

图1 高技术产业贸易竞争力及其影响因子得分情况

A级高技术产业的技术强度因子贡献相对其他综合因子而言较弱，若要提升A级高技术产业贸易竞争力就要加大这些产业的技术研发投入。B及产业绩效因子贡献不够突出，所以在巩固其行业规模和技术强度优势基础上，提升其市场绩效是增强其贸易竞争实力的良策。C级产业若要争取较好的贸易竞争实力，其4个影响因子均亟待改进。

[1]徐道炜，刘金福，洪伟.基于突变级数法的福建省自然保护区与森林公园生态服务功能综合评价[J].福建农林大学学报(自然科学版)，2011，（5）.

[2]肖彦.基于突变级数法的钢铁企业经济绩效评价[J].会计之友，2011，（20）.

[3]朱顺泉.基于突变级数法的上市公司绩效综合评价研究[J].系统工程理论与实践，2002，（2）.

[4]郑光凤，徐玲.促进中国高技术产品出口的对策[J].黑龙江对外经贸，2010，（2）.

[5]戎梅.技术创新对我国高技术产业出口竞争力的影响[J].财经界（学术），2010，（5）.

[6]秦臻，秦永和.中国高技术产业国际竞争力分析[J].中国软科学，2007，（4）.

[7]张霞，胡贤辉，张琳，蔡根女.湖北省高技术产业投入产出动态评价[J].统计与决策，2006，（22）.

[8]马力，常相全，王悦.高技术产业风险投资项目择优的评价模型[J].统计与决策，2006，（1）.

[9]彭宜新，周珊刚.中国高技术产业发展战略再认识[J].统计与决策，2003，（5）.

[10]赵玉林，张倩男.我国高技术产业发展的重点领域[J].统计与决策，2008，（6）.