凸多面体不确定混合时滞系统的均方指数稳定

郭晓宝， 焦贤发， 周堂春

（1.合肥工业大学 数 学学院，安徽 合 肥 230009；2.陆军军官学院 数 学教研室，安徽 合 肥 230031）

0 引 言

众所周知，在工程、生物系统以及信号处理（如多径传播和数据通信）领域中经常发生时滞的现象，这类现象可能导致实际系统的不稳定和震荡。同时，根据时滞发生的方式，可以划分为时变时滞和分布时滞。近年来，研究Markov跳变参数下时滞系统的稳定是控制领域的热点课题之一［1－4］。在 Markov跳变参数系统中，文献［5］研究了带有离散时滞的线性不确定系统鲁棒稳定及可镇定的充分条件；文献［6］研究了分布时滞系统的鲁棒可镇定充分条件；文献［7－8］研究了时滞依赖于模态系统的指数稳定性条件；在线性实常参数凸多面体不确定系统中，文献［9］讨论了离散时滞和时变延迟的鲁棒稳定性。已有的研究涉及了带有Markov跳变参数连续系统的鲁棒稳定性问题或实常矩阵凸多面体不确定系统下的鲁棒稳定性问题。

本文综合考虑了Markov跳变参数下，带有时变与分布时滞的混合时滞类凸多面体不确定系统，通过构造Lyapunov－Krasovskii候选函数，利用线性矩阵不等式方法，给出系统均方指数稳定的充分条件。

1 问题描述与假设

假设1｛rt，t≥0｝为定义在一个带有自然流的完备全概率空间（Ω，F，｛Ft｝t≥0，P）上，取值于有限维状态空间S＝｛1，2，…，N｝，且右连续

Markov过程，其模态转移概率为：

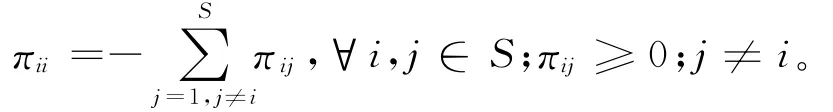
考虑在全概率空间（Ω，F，｛Ft｝t≥0，P）上一类具有混合时滞的Markov跳变参数下的凸多面体不确定系统为：

其中，x（t）∈RN为系统的状态向量；初始条件φ（t）∈RN为在区间［－h，0］上的连续向量函数；ω（t）为在（Ω，F，｛Ft｝t≥0，P）上独立于状态x（t）的维纳过程，满足

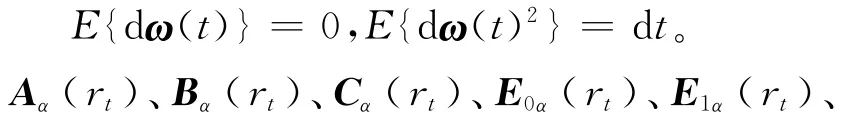
E2α（rt）为含参数不确定性且依赖于模态rt的适当维数矩阵，假设其可以表示为若干个顶点矩阵的凸组合，即

其中，Ai（rt）、Bi（rt）、Ci（rt）、E0i（rt）、E1i（rt）、E2i（rt）为顶点矩阵，i＝1，…，N。

d（t）、h（t）分别为系统时滞，且满足条件：

定义1 系统（1）为均方指数稳定，如果存在正的常量a＞0和b＞0，使得对于系统（1）的每个解x（t；φ）满足：

引理1 对常值矩阵J＞0，任意标量β＞0，向量函数ν：［0，β］→Rn有［10］：

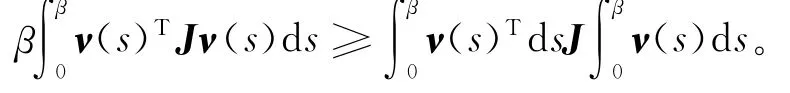
引理2 （Schur）对给定的对称矩阵［11］

其中，S11∈Rr×r，以下3个条件是等价的：

（1）S＜0。

（2）S11＜0，S22－ST12S－111S12＜0。

（3）S22＜0，S11－S12S－122ST12＜0。

2 主要结论

对于系统（1），任取rt＝i∈S，则系统（1）的等价形式为：

其中

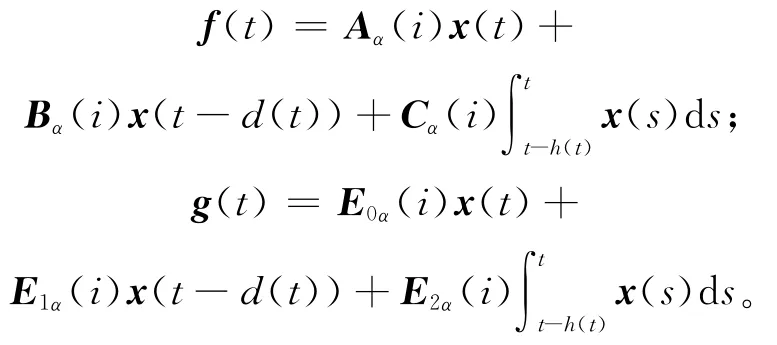
定理1 如果∀i∈S，存在矩阵Pl（i）＞0，Ql＞0，Rl＞0（l＝1，2，…，N），使得以下线性不等式成立，即

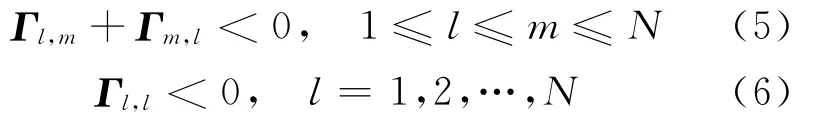
其中

则系统（4）为均方指数稳定。

证明 对 系 统 （4），考 虑 Lyapunov－Krasovskii候选函数：

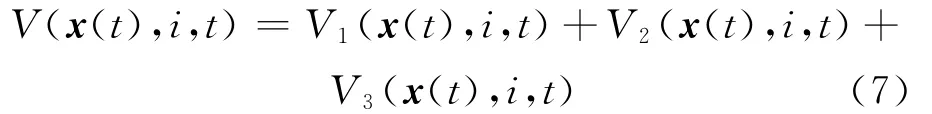
其中

其中，Pα（i）、Qα、Rα为含凸多面体不确定性的适当维数矩阵，形式如下：

由引理1，则有：

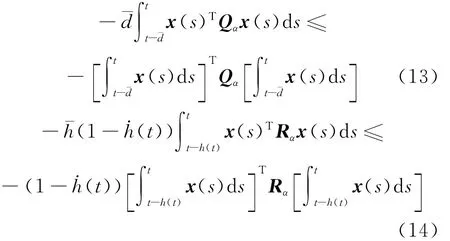
由（3）式、（9）～（14）式，可得：

其中

由（5）式和（6）式，得：

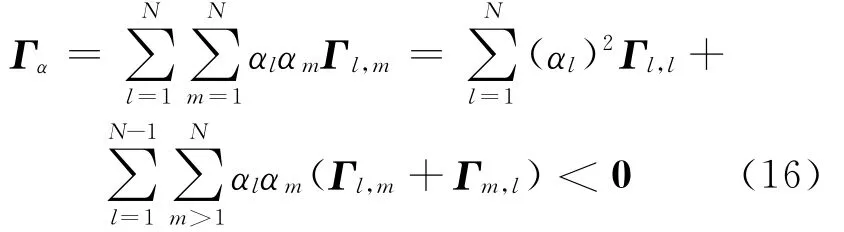
其中

由引理2、（16）式，可得Φ＜0。

设α0＝λmin（－Φ）＞0，由（15）式，可得：

由（7）式知，存在标量α1＞0，α2＞0及λm＝（Pα（i））｝，使得：

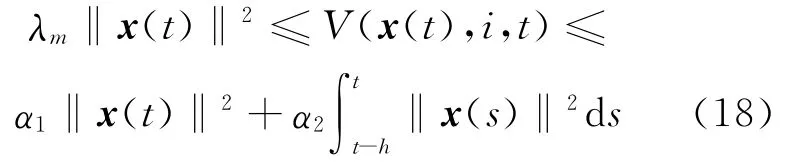
选取合适的β＞0，使得：

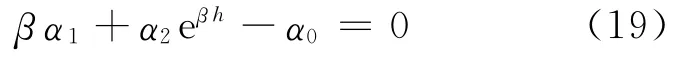
由（17）式、（19）式，对eβtV（x（t），i，t）求导，并取其数学期望得：

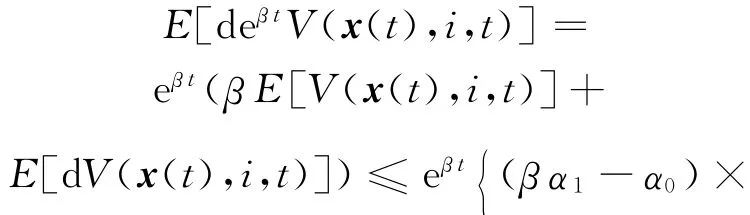
对（20）式两边从0到T积分得：

由（21）式、（22）式，得：

即

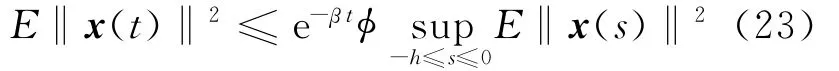
其中，φ＝（α1＋α2h＋α2heβh）／λm。

由定义1，系统（4）为均方指数稳定。

3 数值例子

考虑Markov参数下带有混合时滞的凸多面体不确定系统（1）二维的数值例子。

例1 取Markov跳变的状态空间S＝｛1，2｝，各系数矩阵及参数为：

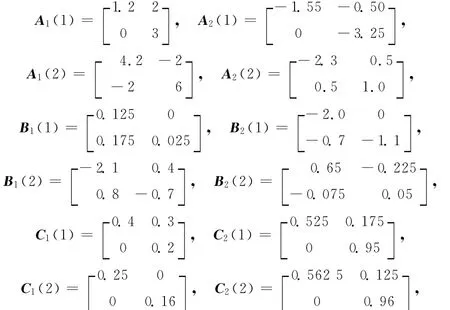
选取满足（7）式、（8）式的矩阵为：

运用Matlab中的LMI工具箱可得：

通过验证满足定理2的条件，故系统（1）为均方指数稳定。

例2 当系统（1）中Cα（rt）、E0α（rt）、E1α（rt）、E2α（rt）项为零矩阵时，文中系统（1）转化为文献［12］中系统（1）的情形，对文献［12］中数值例子利用本文所给方法，运用Matlab中的LMI工具箱可得：

结果满足文献［12］中定理1条件，表明文献［12］中系统均方指数稳定。

4 结束语

本文针对Markov跳变参数下同时具有时变与分布时滞的凸多面体不确定系统，通过构造Lyapunov－Krasovskii候选函数，利用线性矩阵不等式方法，得到该类带有混合时滞的凸多面体不确定系统的均方指数稳定的充分条件。数值例子表明此方法的可行性与有效性。

［1］ Mao X.Exponential stability of stochastic delay interval systems with Markovian switching［J］.IEEE Trans Autom Control，2002，47：1604－1612.

［2］ Boukas E K，Liu Z.RobustH∞control of discrete－time Markovian jump linear systems with mode－depended timedelays［J］.IEEE Trans Autom Control，2001，46：1918－1924.

［3］ Wu Z，Su H，Chu J.Robust exponential stability of uncertain singular Markovian jump time－delay systems［J］.Automatica Sinica，2010，36（4）：558－563.

［4］ Mao X，Matasov A，Piunovskiy A B.Stochastic differential delay equations with Markovian switching［J］.Bernoulli，2000，6：73－90.

［5］ Boukas E K，Liu Z.Robust stability and stabilizability of Markov jump linear uncertain systems with mode－dependent time delays ［J］.Journal of Optimization Theory and Applications，2001，109（3）：587－600.

［6］ Shen H，Wu S，Song X，et al.Delay－depended robust stabilization for uncertain stochastic switching systems with dis－tributed delays［J］.Asian Journal of Control，2009，11（5）：527－535.

［7］ Wang Y，Zhang H.H∞control for uncertain Markovian jump systems with mode－dependent mixed delays［J］.Progress in Natural Science，2008，18：309－314.

［8］ Wang Z，Liu Y，Liu X.Exponential stabilization of a class of stochastic system with Markovian jump parameters and mode－dependent mixed time－delays［J］.IEEE Trans Automatic Control，2010，55（7）：1656－1662.

［9］ Li H，Chen B，Zhou Q，et al.Delay－dependent robust stability for stochastic time－delay systems with polytopic uncertainties ［J］.Robust Nonlinear Control，2008，18：1482－1492.

［10］ 徐启敏，焦贤发.不确定双线性随机离散时间系统的鲁棒控制［J］.合肥工业大学学报：自然科学版，2011，34（6）：949－953.

［11］ Boyd S，Ghaoui L E，Feron E，et al.Linear matrix inequality in system and control theory［M］.Philadelphia：SIAM，1994：7－9.

［12］ Li H，Zhou Q，Chen B，et al.Parameter－dependent robust stability for uncertain Markovian jump systems with time delay ［J］.Journal of the Franklin Institute，2011，348：738－748.