基于平稳α-混合左删失数据众数核估计的渐近正态性
李成好, 汪 超, 凌能祥
(合肥工业大学 数 学学院,安徽 合 肥 230009)
设(Y,T)是R×R上的一对随机变量,其分布函数分别为F、G,两者均未知;并设Y关于Lebesgue测度的未知密度函数f。当且仅当Y≥T时,Y和T都能被观测到,否则,两者都观测不到。当有n个观测数据(Yi,Ti),i=1,2,…,n时,可能实际采集的数据是N个(其中N≥n,N未知),即(Y1,T1),(Y2,T2),…,(YN,TN),其中,(Yi,Ti),i=1,2,…,n与随机变量(Y,T)同分布。此时称样本(Yi,Ti),i=1,2,…,n为随机左删失数据,并称随机变量Y为观测变量,T为随机删失变量,由此建立的模型为随机左删失模型。
左删失数据模型广泛出现在天文学、经济学、流行病学及生物统计学中,很多学者对此问题开展了大量的研究工作。
近年来,基于删失数据的众数核估计的研究取得了一系列成果。文献[1]在iid场合下建立了右删失数据众数非参数核估计的渐近正态性;文献[2]得到了iid场合下右删失数据的条件密度函数和条件众数非参数核估计的强一致收敛性;文献[3]研究了相依结构下右删失数据 Kaplan-Meier估计的渐近性;文献[4]解决了右删失数据分布函数的估计问题;文献[5]给出了iid场合下左删失数据众数非参数核估计的渐近性;文献[6]建立了iid场合下左删失数据的条件密度函数和条件众数非参数核估计的强一致收敛性,并获得了条件众数估计的渐近正态性;文献[7]得到了α-混合结构下左删失数据的密度函数和众数核估计的强一致收敛性;文献[8]建立了α-混合结构下右删失数据众数非参数核估计的强一致收敛性;文献[9]建立了α-混合结构下左删失数据的条件众数非参数核估计的渐近正态性。
本文在现有文献的基础上,研究基于α-混合左删失数据时众数非参数核估计的渐近正态性。
设{Zi,i≥1}为一随机变量序列,为由{Zj,i≤j≤k}生成的σ代数。混合系数α(n)=,k∈N}。如当n→∞时α(n)→0,则称该序列为α-混合序列,又称强混合序列。它是目前文献所见混合条件中最弱的。许多随机过程都满足α-混合条件,如ARMA过程就是强几何混合过程,即∃0<ρ<1,使得α(k)=O(ρk);在遍历性条件下阈值模型、EXPAR模型、简单的ARCH模型及双线性马尔科夫模型都是强混合的。本文假设观测样本(Yi,Ti),i=1,2,…,n是一平稳α-混合序列,在一定的条件下,建立了其众数非参数核估计的渐近正态性。
在左删失模型中,得到随机n个观测数据(这里n是已知的,即使是随机的),但实际观测的样本数N是未知的。令P表示关于N个完全样本的概率测度,P*表示关于n个删失样本的概率测度;同样,令E和E*分别表示关于P和P*的期望,并且用星号(*)表示关于n个删失样本的分布函数。令η:=P(Y≥T),称η为删失剩余率。
在左删失样本下,文献[10-12]给出了(Y,T)的联合分布函数为:

其中,t∧u=min(t,u),而它们的边际分布为:
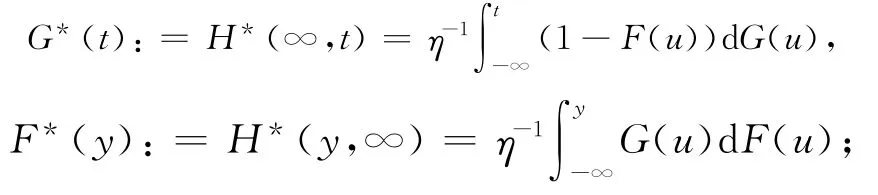
其估计分别为:

其中,IA表示集合A的示性函数。
令f*为观测变量Y的密度函数的核估计,定义为:
其中,K为定义在R上的概率密度函数(被称作核函数);hn:=h表示窗宽,满足:n→∞时h→0。
类似于文献[7]及其所引参考文献,现对任意分布函数L,定义其支撑端点:
当且仅当满足条件:aG≤aF,bG≤bF且时,F和G才能被完全估计。则有:

记

它的经验估计为:

由文献[7],在独立场合下,F、G的非参数极大似然估计为:
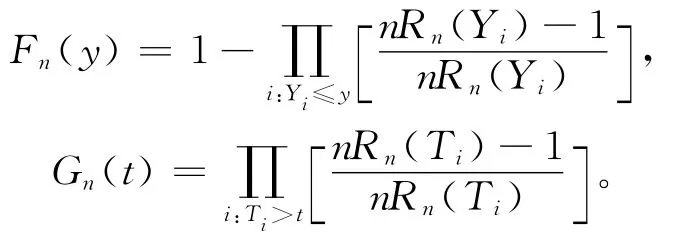
由于N未知无法计算,但由(2)式,得文献[7]说明了与y的选择无关,即对任意的y只要Rn(y)≠0,^ηn就能得到,并给出了
1 符号和估计
在左删失模型下,由文献[7],(1)式不再适合估计密度函数f(·),基于(Yi,Ti),需要构造其新估计(y)。基于文献[7],有估计量:


然而,由于G(·)和η未知,故(3)式和(4)式没有实用价值。类似于文献[7]的思想,得
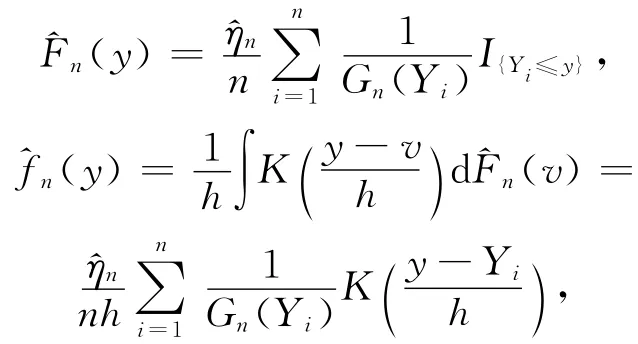
其中,对∀i,Gn(Yi)≠0,于是,众数核估计为=
另一方面,分别对(y)和(y)求一阶、二阶导数
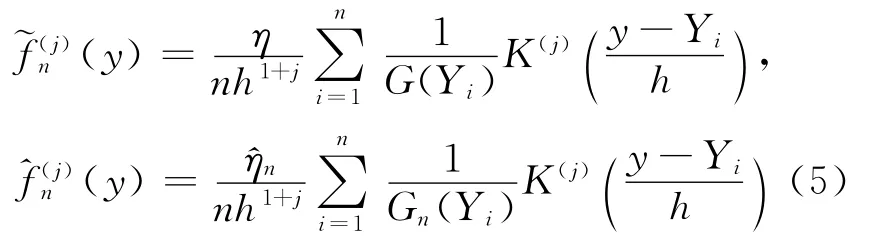
其中,j=1,2。对·)作Taylor展开得:
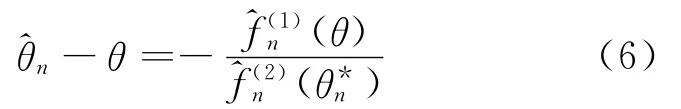
2 假设和结论
假设aG≤aF,bG≤bF,H=[a,b]是一个紧集,使得H⊂Ω={y:y∈[aF,bF]},假设条件如下:
A1 核函数K(·)在H上有界,三阶可微,关于指数β>0Lipchitz连续,满足|u|→∞时|u|K(u)→0;
A2 ∫DK(t)dt=1,∫DtK(t)dt=0。
B1f(·)在H上四阶连续可微,且
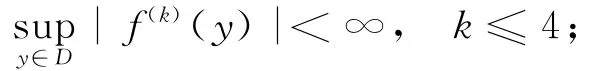
B2 对于众数θ,f(2)(θ)≠0;
B3 (Yi,Yj)的联合密度函数存在,且存在与(i,j)无关的C使 得:
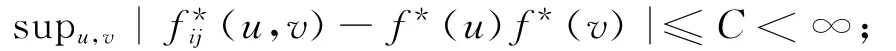
B4 对于∀j≤1,令fj(·,·)表示(Y1,Y1+j)的联合密度函数,对∀y∈H,(y1,y2)∈U(y)×U(y)满足fj(y1,y2)≤C,其中U(y)为y的邻域。
C1 {Yi,i≥1}是平稳的α-混合随机变量序列,混合系数为α(n);
C2 {Ti,i≥1}是一列iid删失变量,具有连续分布函数G,且与{Yi,i≥1}独立;
C3 α(n)满足:存在正整数q:=qn,使得q=o( (nh) ,且lim(nh-1α(q)=0;
n→∞
窗宽h满足:
D1n→∞时
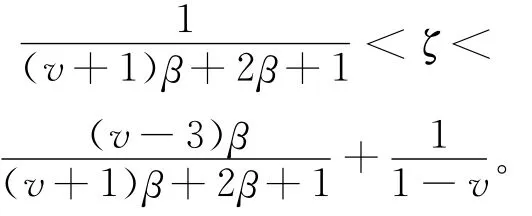
D3(lnn)(lnlnn)=O(nh5)且
假设A是密度函数核估计中常用的条件;假设B3是解决协方差问题常用条件;假设C是α-混合删失数据问题常用假设,其中假设C3、C5是证明α-混合假设下渐近正态性的常用假设,见文献[13];假设D1是建立引理1的重要条件,D2保证引理2对Fuk-Nagaev不等式的处理,D3建立引理4中的收敛速度。
定理1 如果条件A1~A2、B1~B4、C1~C5、D1~D2成立,则

其中,j=1,2。
此处j=0时结论也成立,见文献 [ 7]。
定理2 在定理1的条件下,如果D3满足,则有:


3 模拟研究
为了更清楚地展现在有限样本下对θ的估计效果,将对上面的主要结论进行模拟研究。在第1部分给出估计的均方误差(GMSE),分析其渐近性;第2部分通过频率直方图和概率图研究估计渐近正态表现。为了得到一个α-混合序列,利用AR(1)模型生成数据,具体过程如下:生成εi~N(0,0.92),Y1=ε1,Yi=0.1Yi-1+εi,i=2,3,…,n。Ti~N(μ,1),i=1,2,…,n,其中,μ的选取由不同的η决定。核函数K(·)选用Gaussian核。
3.1 渐近性
对模型分别取样本量n=200,500。数据的删失剩余率η≈50%,90%,窗宽h=n-1/2,n-1/3,n-1/4,各模拟m=200次,计算估计^θn的均方误差GMSE=-θi)2,结果见表1所列。
表1 估计 的GMSE

表1 估计 的GMSE
η/% n h=n-1/2 h=n-1/3 h=n-1/4 200 0.059 3 0.154 1 0.252 2 500 0.015 6 0.097 8 0.198 3 90200 0.010 6 0.081 2 0.180 0 50 500 0.007 0 0.058 5 0.076 0
由表1可以看出:①当删失剩余率和样本量不变时,窗宽h越大估计误差越大;②当删失率剩余和窗宽不变时,样本量n越大估计越好;③当样本量和窗宽不变时,删失剩余率越大估计表现越好。
3.2 渐近正态性
取η≈90%,h=n-1/3,分别令n=200,500,各模拟m=500次,生成直方图和概率点图。对比图1a、图1b,图2a、图2b可以得出结论:
(1)估计的误差分布接近正态。
(2)删失样本量n越大,正态性越好。


图1 直方图

图2 正态概率图
4 主要结果的证明
定理1的证明
该证明由下面的分解式
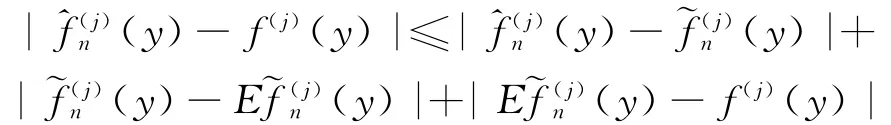
和引理1~引理3得到。
引理1 假设条件 A1,A2,B2,C1~C3,D1成立,则

其中,j=1,2。
证明
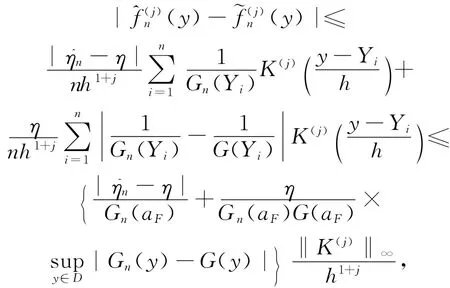
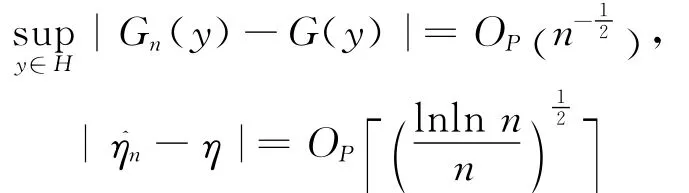
则引理得证。
引理2 假设条件A1,B1~B3,C1,C4,D1~D2成立,则

其中,j=1,2。
证明 设紧集H被ln(ln有限)个半长度为的区间覆盖,其中β为Lipchitz指数。令Uk:=U(yk,wn),1≤j≤ln为以点yk为中心wn为半长的区间。因为H有 限,故∃M>0,使得wnln≤M,对∀y∈H,∃Uk包含它,使得|y-yk|≤wn。令

则

因此


接下来证明:

由 A 1知K(j)(j=1,2)满足Lipschitz条件,则
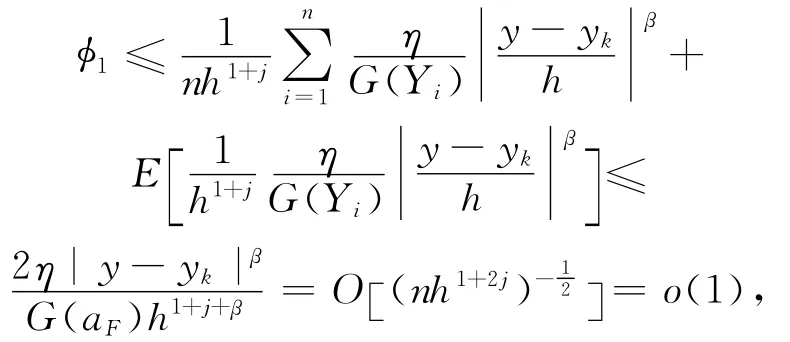
因此φ1项得证。
下面再研究φ2项。
令ξi=nh1+jΔi(yk),则|ξi|∞。由相依序列的 F uk-Nagaev不等式[14],对∀ε>0,r>0,可得:

其中,

由 A 1,B1,B2及变量代换,得
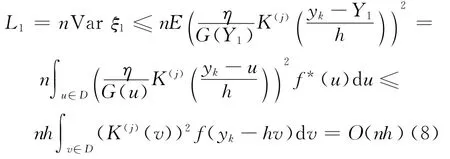
由A1,B3,C1及变量代换,得


由相依序列的协方差不等式[15],显然有:

为了研究L2项,取x表 示 比x大的最小整数,有

由(9)式得:
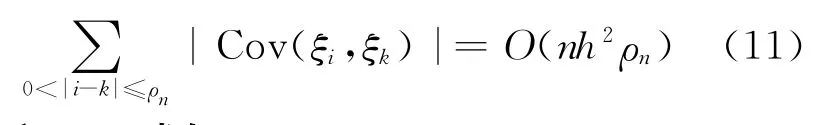
由C4和(10)式知:

根据D2不等式右边知,∃φ>0,使得:
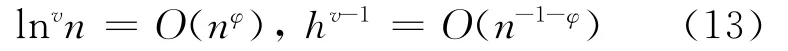
由C4和(11)~(13)式得:

由(8)式、(14)式得:


取r=(lnn)1+c(c>0),由ln(1+x)的 T aylor展开式,(16)式变为:
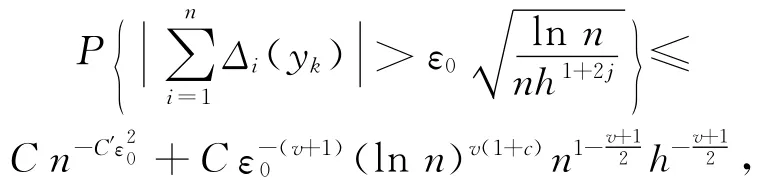
因此,

由D2不等式左边得:

因此对于D2中任意的ζ,φ21是有界的。同理,适当选取ε0=O)得 φ22也有界。因此)<∞。由Borel-Cantelli引理可得:

其中,j=1,2,则引理得证。
引理3 假设条件A2,B1~B2成立,则

其中,j=1,2。
证明 该渐近形式与相依结构无关。由分部积分、变量代换、A3和Taylor展开可得:

4.2 定理2的证明
由(6)式得:
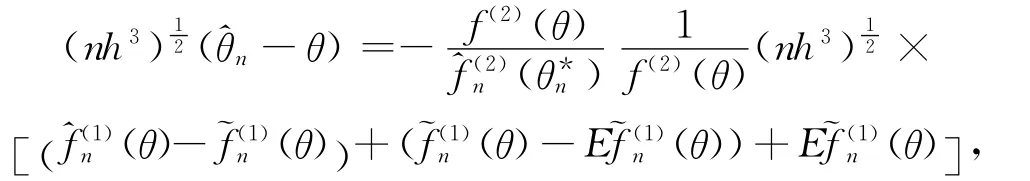
在定理1中令j=2有:

因此在引理1中令j=1有:

再结合下面的引理4和引理5,定理2即证。
引理4 假设条件 A 1,A3,B1~B2,D3成立,则(nh3
证明

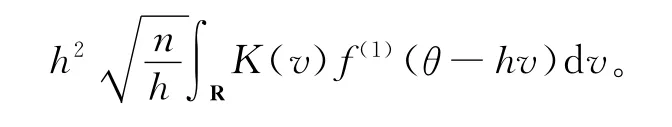
对f(1)(θ-hv)做Taylor展开:
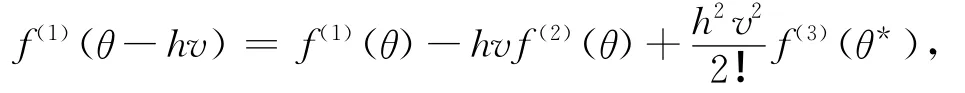
其中,θ*在θ和θ-hv之间。由f(1)(θ)=0,B1,B2和D3得:
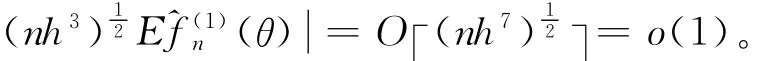
引理5 假设条件 A 1~A2,B4,C2~C4,D1~D2成立,则

证明 这里用Bernstein大块小块方法,参见文献[16-17]。设长度为p=pn的大块和长度为q=qn的小块将集合{1,2,…,n}分割成2ωn+1个子集,其中ω=ωn=[n/(p+q)]。C3显示了存在正 整 数 列δ → ∞,使 得δq=o((nh)1),nnP2。令 大 块 长 度p=pn=,则]
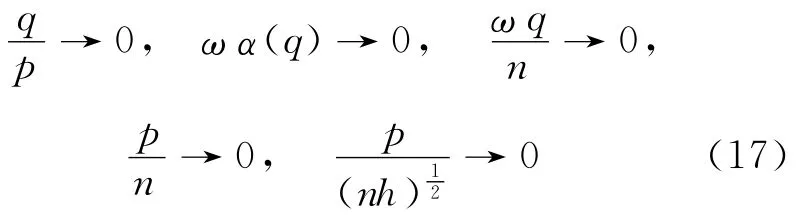
令
其中,km=(m-1)(p+q)+1,lm=(m-1)(p+q)+p+1,m=1,…,ω。则

接下来证明以下结果:


首先证明(18)式,由(3)式可得:
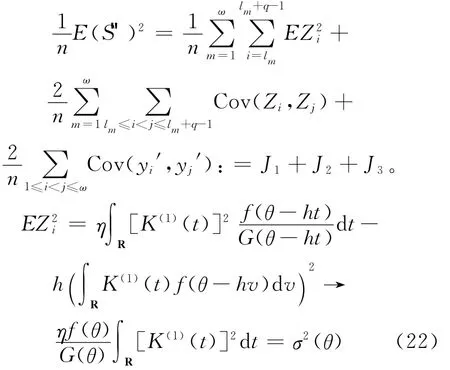
结合(17)式有J1=O(ωq/n)=o(1)。
因为

要证|J2|=o(1),|J3|=o(1),只要证:

下一步,设cn为一整数列且cn→∞,cnh→0,令

则
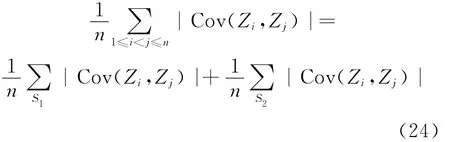
由B4对i<j有:
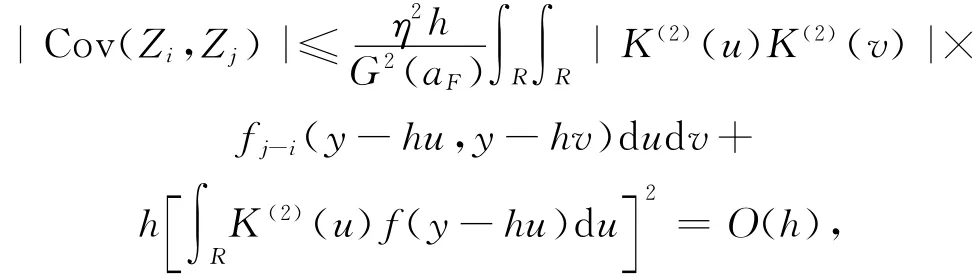
因此:
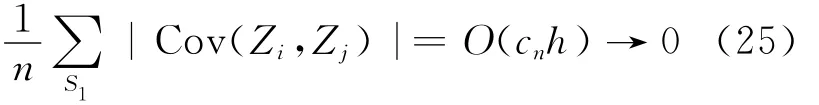
由文献[17]有:
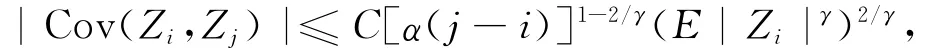
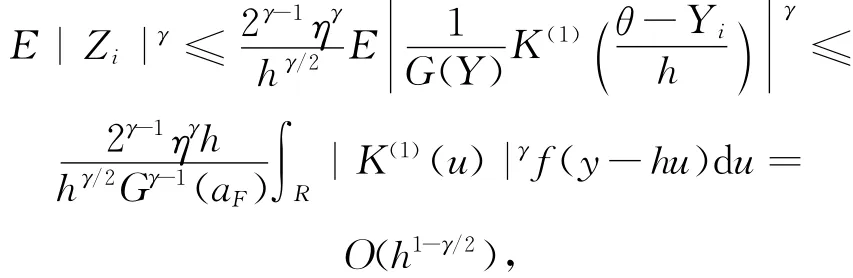
则


由 ( 24) ~ (26) 式 知 (23) 式 成 立, 故|J2|=o(1),|J3|=o(1)。
对于(19)式,由(22)式、(23)式可得:

对于(20)式,由文献[18]和(15)式得:
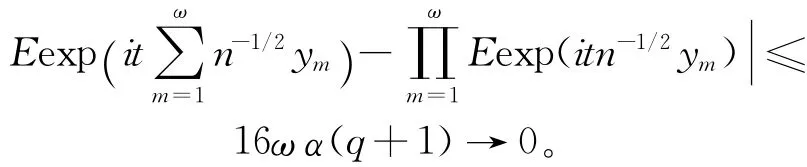
[1] Louani D.On the asymptotic normality of the kernel estimators of the density function and its derivatives under censoring[J].Comm Stat Theor Meth,1998,27:2909-2924.
[2] Ould-Saǐd E,Cai Z W.Strong uniform consistency of nonparametric estimation of the censored conditional mode function[J].Journal of Nonparametr Stat,2005,17(7):797-806.
[3] Cai Z W.Asymptotic properties of Kaplan-Meier estimator for censored dependent data[J].Stat Probab Lett,1998,37:381-389.
[4] Cai Z W.Estimating a distribution function for censored time series data[J].Journal of Multivariate Anal.2001,78:299-318.
[5] Ould-Saǐd E,Tatachak A.On the nonparametric estimation of mode under left truncated model,Technical Report L M P A 2005,No.271[R].Univ du Littoral cote d’Ople,2005.
[6] Ould-Saǐd E,Tatachak A.Asymptotic properties of the kernel estimator of the conditional mode for the left truncated model[J].Statistics & Probability Letters,2007,344:651-656.
[7] Ould-Saǐd,Tatachak A.Strong consistency rate for the kernel mode estimator under strong mixing hypothesis and left truncation [J].Comm Stat Theo Meth,2009,38:1154-1169.
[8] Khardani S,Lemdani M,Ould-Saǐd E.On the strong uniform consistency of the mode estimator for censored time series[J].Metrika,2012,75:229-241.
[9] Liang Hanying,de U~na-A′lvarez J.Asymptotic normality for estimator of conditional mode under left-truncated and dependent observations[J].Metrika,2010,72:1-19.
[10] Stute W.Almost sure representation of the product-limit estimator for truncated data [J].Ann Statist,1993,21:146-156.
[11] Zhou Y.A note on the TJW product limit estimator for truncated and censored data[J].Stat Probab Lett,1996,26:381-387.
[12] Lynden-Bell D.A method of allowing for known observational selection in small samples applied to 3CR quasars[J].Monthly Notices Roy Astronom Soc,1971,155:95-118.
[13] Masry E.Nonparametric regression estimation for dependent functional data:asymptotic normality [J].Stoch Proc Appl,2005,115:155-177.
[14] Ferraty F,Vieu P.Nonparametric functional data analysis theory and practice[M].Berlin:Springer,2006:237.
[15] Bosq D.Nonparametric statistics for stochastic processes:estimation and prediction[M].2nd ed.Berlin:Springer-Verlag,1998:7-8.
[16] 丁 洁,凌能祥.基于相依函数型数据条件均值函数估计的渐近性质[J].合肥工业大学学报:自然科学版,2011,34(7):1104-1107,1116.
[17] Hall P,Heyde C C.Martingale limit theory and its application[M].New York:Academic Press,1980:277-279.
[18] Volkonskii.V A,RozanovY.A.Some limit theorems for random functions[J].Theory Probab Appl,1959,4:178-197.

