基于FPGA离散分数阶傅里叶变换算法的实现*

史兆强，魏增辉，马 壮

（1.河南机电高等专科学校电子通信工程系，河南新乡 453000;

2.黄河水利职业技术学院信息工程系，河南 开封 475003;3.中国电子科技集团公司第二十七研究所，河南 郑州 450047）

1 引言

分数阶傅里叶变换是对经典傅里叶变换的推广，在分析和处理非平稳信号领域有着广泛的应用。1996年Ozaktas等提出了一种计算量与FFT相当的离散算法后，各种分数阶傅里叶变换的离散算法的相继出现，进一步促进了分数阶傅里叶变换在光学信号处理、时频分析在内的多个信号处理领域的发展。至今为止，有关分数阶傅里叶变换已具有比较成熟的快速离散算法，这就为分数阶傅里叶变换能进入数字信号处理的工程实用阶段做了理论基础。近几年的研究文献表明［1］，大多集中在对分数阶傅里叶变换的理论研究上，涉及具体工程实现方面甚少。本文主要在对现有DFRFT算法的分析基础之上，选用Ozaktas等人［2］提出的快速算法，对其做了易于FPGA实现的仿真分析，给出可以直接应用在FPGA上的计算实现。

2 离散分数阶傅里叶变换算法

对于连续的分数阶傅里叶变换定义式［1］如下:

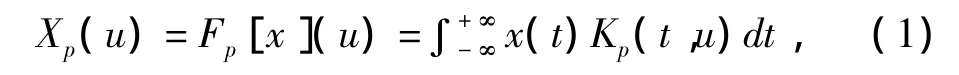
其中

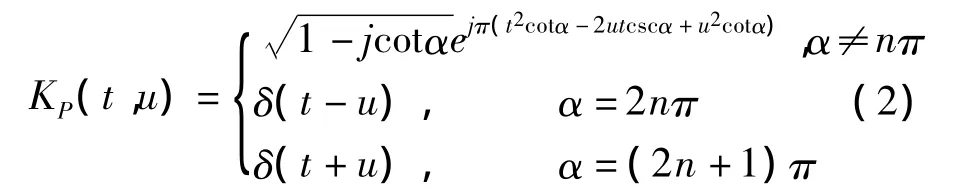
为FRFT变换的核函数，式中α=pπ/2，p为分数阶傅里叶变换的阶数。在数字信号处理的应用中，必须采用离散形式的分数阶傅里叶变换（DFRFT），DFRFT在工程实践中的推广应用很大程度上依赖于灵活高效的快速算法。近年来出现的比较成熟的快速离散算法可分三类［1］:

1）特征分解型，通过取离散傅里叶变换（DFT）核矩阵的特征值和特征向量构造DFT核矩阵的分数幂来计算DFRFT。该类方法能保证分数阶傅里叶变换的大部分性质，但缺点是计算复杂度高，不利于实时处理。

2）线性组合型，通过对某些特定阶数的DFRFT的线性组合得到任意阶数DFRFT，缺点是计算精度与连续变换相比误差是最大的。

3）离散分解型，由Ozaktas等人提出，通过数学推导将连续FRFT计算转化为一个调制信号与chirp信号相卷积形式，最后利用FFT运算得到分数阶傅里叶变换结果。

在目前已有的各种DFRFT算法中，离散分解型由于计算精度高、计算负担小、便于FPGA实现而成为主流算法。

3 离散分解方法理论基础

分解法是根据FRFT表达式，将FRFT分解为信号的卷积形式，从而利用FFT来计算FRFT。这种算法的机理在进行FRFT计算之前须先对原始信号进行量纲归一化处理［3］。理论上，任何信号和它的傅里叶变换不可能是同时紧凑的。实际中需要处理的信号往往是时限和带限的。在实际信号处理时，假定原始连续信号在时间和频率轴上是紧凑的，其时域限定在区间［－△t/2，△t/2］，频域限定在［－△f/2，△f/2］，△t和△f分别表示信号的时宽和带宽。则时宽带宽

4 快速算法的理论分析

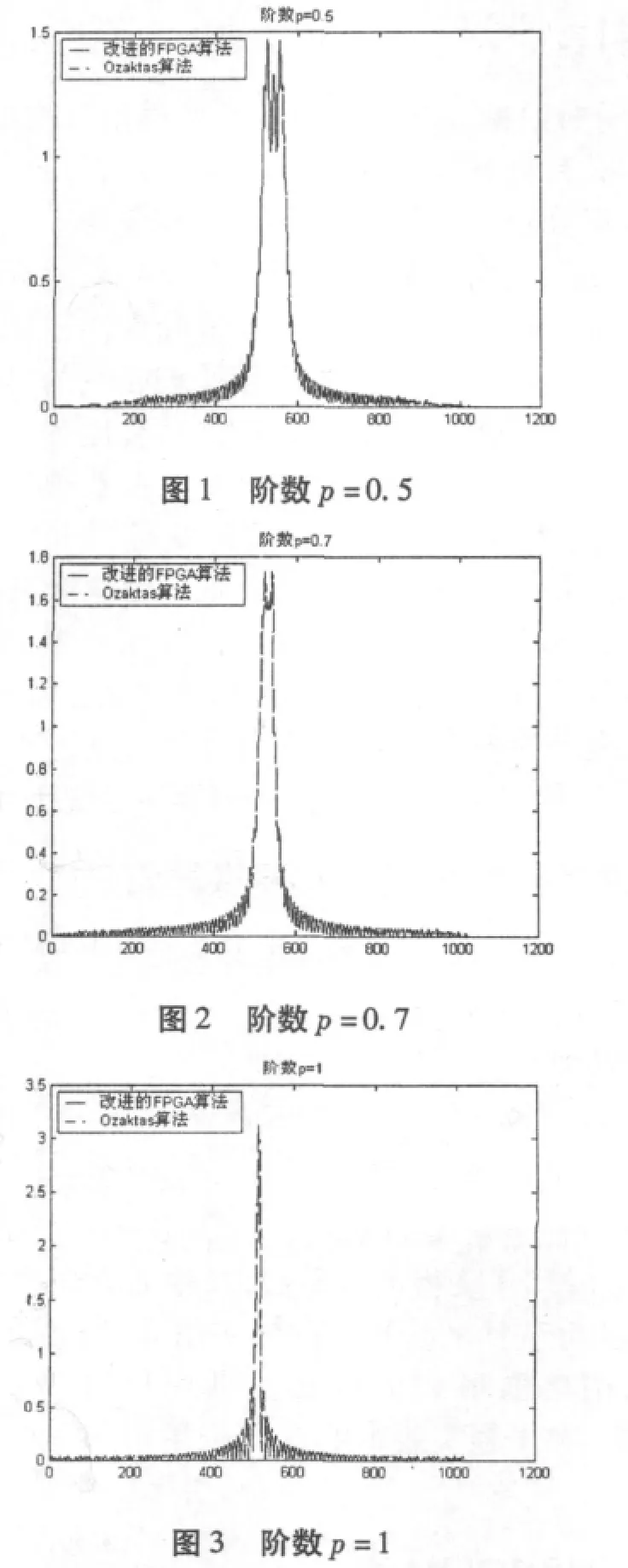
算法和原来Ozaktas的经典算法误差不大，而且对输入信号为K点的复数情况，计算实数乘法的运算量［4］为4Llog2l+4L+16N+4K+4，在原来经典算法基础上加以改进，更易于FPGA的实现。

5 快速算法FPGA的详细实现

结合快速算法的实现流程，用FPGA实现时可按图4所示进行。在用FPGA做DFRFT基本上需要用到FFT核、corddic核［5］。时序上，首先做预处理，然后对信号进行插值滤波，同时产生chirp1信号，二者相乘的结果再与使用corddic核算出的chirp2信号做线性卷积，最后经过IFFT变换以及抽取的结果就是分数阶傅里叶的结果。

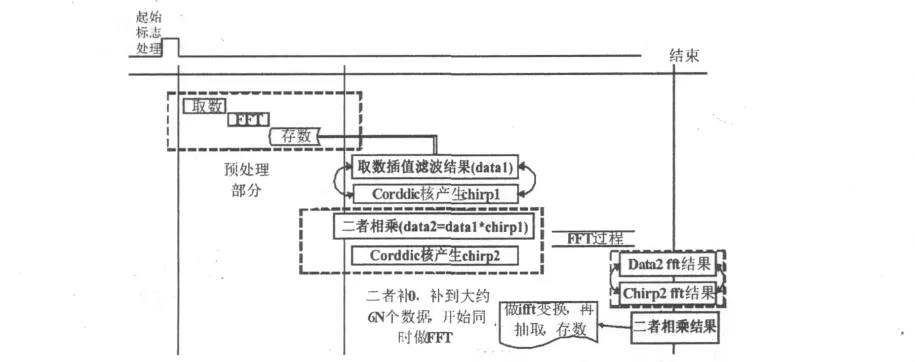
图4 DFRFT算法的FPGA实现流程图

总体来说，可用3个单独的FFT核，从图4中可知预处理时候的FFT和后面的FFT过程在时间上并不冲突，如果为节省资源，用两个FFT核也可满足需要。

6 结论

在对离散分数阶傅里叶快速算法理论分析基础之上，给出了改进的快速离散算法并可应用在FPGA上处理实现。在保证算法精确度的条件下，该算法运算量降至最小。同时，用FPGA实现更适用于在信号处理要求比较高的情况下应用，模块化的IP核也保证了算法的运行速度，能进一层次简化开发的流程，可在今后实际工程应用中高效利用，进而满足精度和实时性的要求。

（责任编辑吕春红）

［1］陶然，邓兵，王越.分数阶傅里叶变换在信号处理领域的研究进展［J］.中国科学 E辑信息科学，2006，36（2）:113－136.

［2］Ozaktas H M，Arikan O，Kutaym A，et al.Digital computation of the fractional傅里叶 transform［J］.IEEE Tran Signal Processing，1996，44（9）:2141－2150.

［3］陶然，齐林，王越.分数阶傅里叶变换的原理与应用［M］.北京:清华大学出版社，2004.

［4］陈鹏，侯朝焕，梁亦慧，等.离散分数阶傅里叶变换快速算法的DSP详细实现［J］.应用光学，2007，28（2）:146－150.

［5］徐欣，于红旗，易凡，等.基于FPGA的嵌入式系统设计［M］.北京:机械工业出版社，2004.