轴向尺寸对泡沫铝动静态力学性能的影响＊

王鹏飞，胡时胜

（中国科学技术大学中国科学院材料力学行为和设计重点实验室，安徽 合肥230027）

泡沫材料的应力应变曲线可分为弹性区、屈服平台区、致密区三个阶段［1］。与其他材料不同的屈服平台区，使得泡沫材料具有良好的吸能特性，广泛应用在汽车船舶、航空航天、铁路交通等领域。

由于泡沫材料的孔径较大，在一定的小尺度范围内，连续介质力学理论不再实用，尺寸的影响不可忽略。T.Mukai等［2］对闭孔泡沫铝进行实验得到，随着厚度的减小，材料具有更高的强度，这是由于小尺寸试件具有更高的比表面积。P.R.Onck等［3］和E.W.Andrews等［4］建立了蜂窝材料的六边形模型，从理论和实验上探讨了横向尺寸（垂直于加载方向）对材料性能的影响。横向尺寸越大，未受约束的胞孔自由表面所占比例越小，试件内部完整胞元所需分担的力越小，对应的弹性模量、压缩应力也越大。当试件的尺寸大于5个胞孔直径时，随着尺寸的增加，应力基本趋于恒定。C.Chen等［5］研究了在夹心板约束下加载方向泡沫铝厚度的影响，随着泡沫层厚度的减小，屈服强度提高，这是由于夹心板和泡沫材料连接处的约束增加了胞壁的屈曲能力。P.J.Tan等［6］通过直接撞击实验得出，在低速撞击下，小尺寸试件对应更高的应力，但在高速撞击下，惯性效应成为应力增强的主要原因，此时厚度影响甚微。

分离式Hopkinson杆是研究材料动态力学性能最常用的实验装置［7－8］，建立在一维应力波理论与应力均匀性两个假定的基础上。实验中试件的厚度必须足够薄，否则在加载的过程中难以实现试件的应力均匀性假定，无法将惯性效应（波动效应）与应变率效应解耦［9－11］。

综上所述，研究泡沫材料在高应变率下的动态力学行为时，不同的试件尺寸可能会得出千差万别的实验结果。一方面，从连续介质力学的角度，试件的尺寸越大越好；另一方面，动态实验中大尺寸必然计及惯性效应（即波动效应）。刘耀东等［12］通过数值模拟，重点讨论了惯性效应对应力增强的影响。近来，实现Hopkinson杆中波动效应与应变率效应的解耦是泡沫材料实验中的一个重大问题。

本文中，首先通过准静态实验，从泡沫材料密度分布离散性的角度分析尺寸的影响。对密度均匀性较差的材料，厚度的影响明显，不适宜用来研究诸如温度、应变率等因素对性能的影响。接着利用石英晶体片测量试件在动态加载过程中的应力均匀性［13－14］。随着尺寸的增大，应力平衡过程需要更长的时间，以致无法满足应力均匀性假定，并在此基础上讨论泡沫材料的应变率效应。

1 材料的密度均匀性分析

1.1 试件的密度分散性

采用上海奥深特金属复合材料科技有限公司生产的泡沫铝材料，原材料尺寸为400mm×400mm×60mm，孔径介于2～5mm。共选取了两块原材料，加工为直径32mm、厚12、15、20和32mm 的试件，直径方向有约十个胞孔的长度。原材料1有73个试件，由图1（a）可见，试件密度分散性较大（300～850mg／cm3）。原材料2有81个试件，由图1（b）可见，试件密度的离散性较小（290～370mg／cm3），密度分布基本符合正态分布。

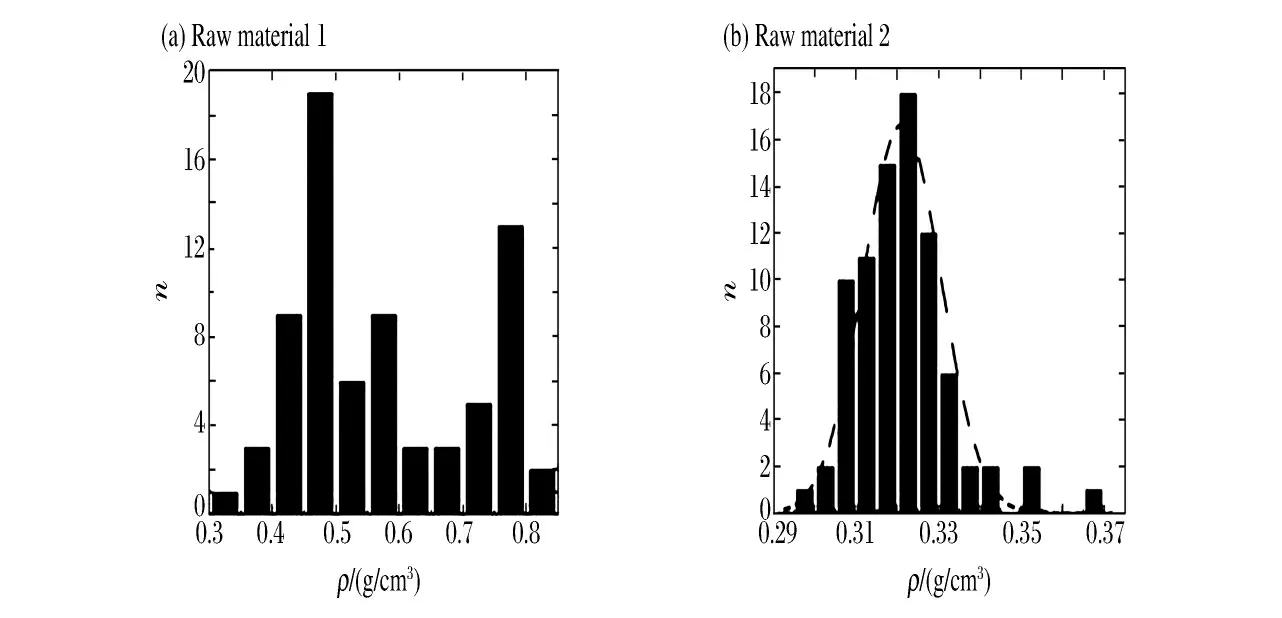
图1 原材料加工成试件后的密度分布Fig.1 Density distribution of specimens processed from the the raw materials

1.2 试件的尺寸效应

原材料1加工后试件的密度主要集中在450～500mg／cm3之间（见图1（a）），选取密度近似、厚度不同的试件，得到材料在准静态下的应力应变曲线，如图2（a）所示。厚12mm 试件的曲线重合性较好，而厚32mm 的试件，坍塌应力和平台应力都有明显下降，并且重合性较差。这主要由于试件局部密度分布不均匀，随着轴向尺寸的增加，缺陷增多，试件更易变形。这种尺寸敏感性主要由材料本身密度分布不均匀造成，此类离散性较大的材料不太适合用来研究其他因素对材料宏观性能的影响。

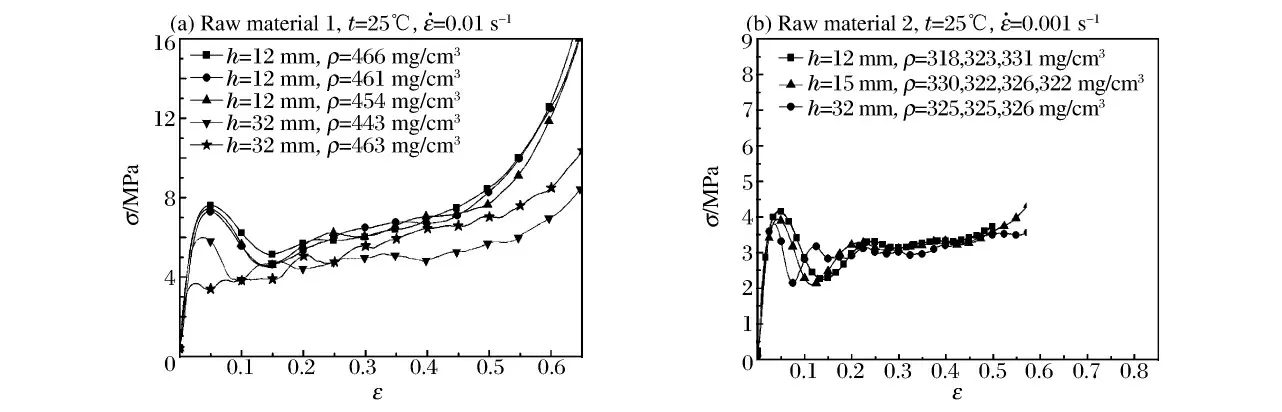
图2 原材料加工成试件后的应力应变曲线Fig.2Stress－strain curves of specimens processed from the the raw materials

原材料2加工后试件的密度主要集中在310～330mg／cm3之间（见图1（b）），选取密度近似、厚度不同的试件，得到材料在准静态下的应力应变曲线，如图2（b）所示。随着厚度的增加，坍塌应力和平台应力都略有下降。当厚度小于15mm 时，应力下降明显；当厚度大于15 mm 时，应力下降趋缓（见图3）。分析表明，影响泡沫材料应力应变曲线的因素主要为试件端部摩擦效应。试件越薄，端面摩擦对胞孔变形的影响越大，使试件强度提高，而密度的尺寸效应不明显。

图3 原材料2试件不同厚度的应力Fig.3Stresses of raw material 2

因此，研究泡沫材料在准静态和动态下的力学行为时，选取原材料2加工后的试件。

2 泡沫铝在动态加载下应力均匀性分析

2.1 利用石英传感器测量试件两端的应力

经典的Hopkinson杆实验技术基于一维应力波理论和应力均匀性两个假定。根据一维应力波的理论，可以得到入射杆与透射杆加给试件两端的力

式中：A 为杆面积，E 为杆弹性模量，εi（t）是入射波应变信号，εr（t）是反射波应变信号，εt（t）是透射波应变信号。

由于大孔径泡沫铝的强度较低，实验中透射信号εt（t）微弱，需用半导体应变片测量。而入射信号εi（t）和反射信号εr（t）的幅值相当，无法通过公式（1）得到精度较高的试件左端的应力。

对于软材料，试件两端应力均匀性的测量一般通过在试件与杆接触的端面增加石英薄片［13］测得（见图4）。石英片可以检测很微弱的信号，利用石英晶体的压电效应，接入电荷放大器，将力产生的电荷信号转化成电压信号，再通过示波器输出。石英片所受的压力F 与电荷放大器输出电压U 之间的关系为

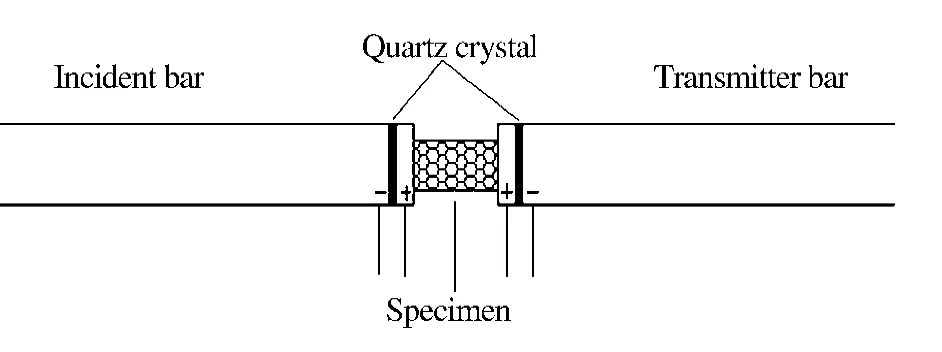
图4 利用石英片测量试件两端的应力Fig.4Stress measurement of specimen ends with quartz piece

式中：d1是电荷放大器的灵敏度系数，k是电荷放大器的输出增益，d11是石英片的压电常数。

利用两片石英片可以测量试件两端的应力，观察试样在动态加载下是否达到应力均匀状态。实验中，子弹长度800mm，杆的直径37mm，石英片的尺寸为Ø37mm×0.2mm。

2.2 动态加载下试件的应力均匀性

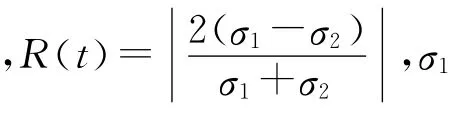
一般而言，当R（t）＜0.05时，可认为应力达到均匀。宋力等［10］比较了在矩形、梯形、斜坡形三种加载波形下达到应力均匀所需的时间，其中梯形加载波应力均匀时间最短。实验中，采用脉冲整形技术，可以实现梯形脉冲加载，减少应力均匀所需的时间。

将入射波起始点移至试件前端面的应力信号起始点，可以观测入射波的上升沿对试件两端应力均匀过程的影响。如图5（a）所示，入射波的上升沿宽度为约150μs，对于厚15mm 的泡沫试件，应力平衡所需的时间约150μs，对应图5（a）中A 区。如图5（d）所示，在初始应力平衡的过程中，应力不均匀度R（t）远大于0.05，到E 点时，R（t）＜0.05，可视试件处于应力均匀状态，E 点正是图5（a）中A、B 区分界线。如图5（a）所示，入射波的平台段约200μs，对应试件应力均匀性较好的阶段，即图5（a）中B 区。

当试件的厚度增加时，试件左右端面更不易实现应力均匀。对厚32mm 的试件（见图5（b）），入射波脉宽（约400μs）的整个过程都无法实现应力均匀，而对厚50mm 的试件（见图5（c）），应力不均匀性更严重（见图5（d））。

如果试件的应力一直处于不均匀状态，则无法将波动效应（惯性效应）和应变率效应解耦，不能够精确得到材料的应变率相关的本构关系。

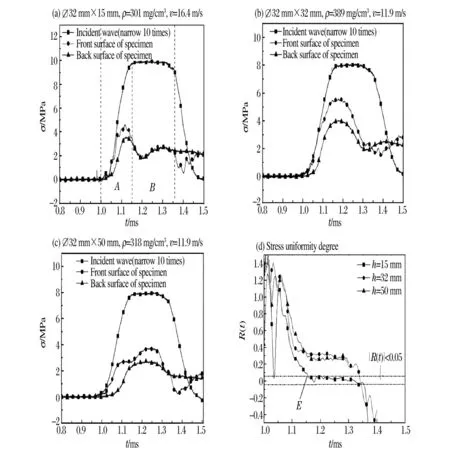
图5 不同厚度试件的应力均匀性Fig.5Stress uniformity in specimens with different sizes

随着试件厚度的增加，材料在动态下的响应更多的是惯性效应造成的。刘耀东等［12］通过数值模拟研究了泡沫材料的三种变形模式，讨论了惯性对应力平台增加的影响。如图5（a）所示，对厚15mm 的试件，开始时左端面的应力大于试件右端面的应力，然后达到应力均匀，对更厚的试件，左端面的应力一直大于右端面的应力，始终无法实现应力均匀。

综上所述，在泡沫铝的动静态实验中选取试件（密度介于315～335 mg／cm3之间）的尺寸均为Ø32mm×15mm。此尺寸的试件，既可忽略前面所讨论的尺寸效应的影响，又能满足动态加载下的应力均匀性假定。

2.3 泡沫铝的应变率效应

在满足Hopkinson杆动态实验的应力均匀性等条件下，可以研究多孔材料的动态力学性能。如图6 所示，采用原材料2 加工的试件，尺寸为Ø37mm×15mm，密度介于315～335 mg／cm3之间，每种应变率对应的曲线都是三个试件（重复性较好）平均后的曲线。

如图6，A 区对应着应力平衡的过程（见图5（a）），此时应变率效应与波动效应尚未解耦。在B区，基本实现应力均匀，满足Hopkinson 杆均匀性假定，因此，可以取B 区的平均应力讨论应变率效应。可见在高应变率下，泡沫材料强度大于低应变率下的强度，表明此泡沫铝具有一定的应变率效应。

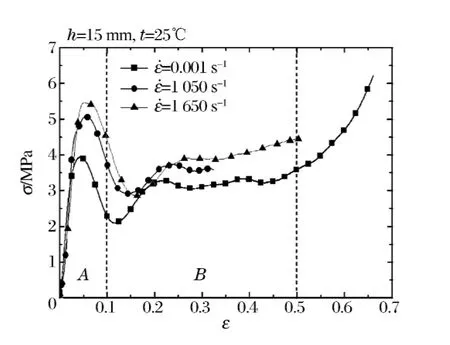
图6 不同应变率下泡沫材料的应力应变曲线Fig.6Stress－strain curves with different strain rates

图6中，无论是动态曲线还是静态曲线，都出现一定程度的震荡，这主要由超轻泡沫铝的泡孔结构引起［15］。随着加载应力的增加，胞壁经历弹性、塑性变形，当应力应变曲线达到峰值后胞孔坍塌失稳，失稳后相邻胞壁相接触，又使应力提高，这反映在应力应变曲线上。

泡沫材料的应变率效应，是基体材料的应变率效应、结构的微惯性、孔内气体共同作用的结果。进一步的工作需结合数值模拟探讨应变率和结构微惯性对应变率效应的影响。

3 结 论

在研究泡沫材料的应变率效应时，泡沫材料的密度分散性对实验结果有很大的影响，只有均匀性较好的原材料才能消除轴向尺寸的影响，得到重复性较好的结果。

利用石英片技术，探讨了低阻抗的多孔材料在Hopkinson杆实验中的应力均匀性。实验表明，随着厚度的增加，试件的应力不均匀度增大，波动效应的影响更明显，在利用分离式Hopkinson杆探讨泡沫材料动态力学性能时需解耦波动效应与应变率效应。

在消除试件尺寸影响和满足应力均匀性假定的前提下，通过实验得出了泡沫铝在高应变率下的力学性能。

［1］ Gibson L J，Ashby M F.Cellular solids：Structures and properties［M］.2nd ed.Cambridge University Press，1997.

［2］ Mukai T，Kanahashi H，Miyoshi T，et al.Experimental study of energy absorption in a closed－celled Aluminum foam under dynamic loading［J］.Scripta Materialia，1999，40（8）：921－927.

［3］ Onck P R，Andrews E W，Gibson L J.Size effects in ductile cellular solids.PartⅠ：Modeling［J］.International Journal of Mechanical Sciences，2001，43：681－699.

［4］ Andrews E W，Gioux G，Onck P R，et al.Size effects in ductile cellular solids.PartⅡ：Experimental results［J］.International Journal of Mechanical Sciences，2001，43：701－713.

［5］ Chen C，Fleck N A.Size effects in the constrained deformation of metallic foams［J］.Journal of the Mechanics and Physics of Solids，2002，50：955－977.

［6］ Tan P J，Reid S R，Harrigan J J，et al.Dynamic compressive strength properties of aluminium foams.PartⅠ：Experimental data and observations［J］.Journal of the Mechanics and Physics of Solids，2005，53：2174－2205.

［7］ Kolsky H.An investigation of the mechanical properties of material at very high rates of loading［J］.Proceedings of the Physical Society of London，1949，B62：676－700.

［8］ 胡时胜.霍普金森压杆技术［J］.兵器材料科学与工程，1991，11：40－47.HU Shi－sheng.Technology of Hopkinson pressure bar［J］.Ordnance Material Science and Engineering，1991，11：40－47.

［9］ Song B，Chen W.Dynamic stress equilibration in split Hopkinson pressure bar tests on soft materials［J］.Experimental Mechanics，2004，44（3）：300－312.

［10］ 宋力，胡时胜.SHPB测试中的均匀性问题及恒应变率［J］.爆炸与冲击，2005，25（3）：207－216.SONG Li，HU Shi－sheng.Stress uniformity and constant strain rate in SHPB test［J］.Explosion and Shock Waves，2005，25（3）：207－216.

［11］ Yang L M，Shim V.An analysis of stress uniformity in split Hopkinson bar test specimens［J］.International Journal of Impact Engineering，2005，31（2）：129－150.

［12］ 刘耀东，虞吉林，郑志军.惯性对多孔金属材料动态力学行为的影响［J］.高压物理学报，2008，22（2）：118－124.LIU Yao－dong，YU Ji－lin，ZHENG Zhi－jun.Effect of inertia on the dynamic behavior of cellular metal［J］.Chinese Journal of High Pressure Physics，2008，22（2）：118－124.

［13］ 林玉亮，卢芳云，卢力.石英压电晶体在霍普金森压杆实验中的应用［J］.高压物理学报，2005，19（4）：299－304.LIN YU－liang，LU Fang－yun，LU Li.The application of quartz transducer technique in SHPB［J］.Chinese Journal of High Pressure Physics，2005，19（4）：299－304.

［14］ Ravichandran G，Subhash G.Critical appraisal of limiting strain rates for compression testing of ceramics in a split Hopkinson pressure bar［J］.Journal of the American Ceramic Society，1994，77（1）：263－267.

［15］ Kanahashi H，Mukai T，Yamada Y，et al.Dynamic compression of an ultra－low density aluminium foam［J］.Materials Science of Engineering，2000，A280：349－353.