可变形电子元件的非线性动力屈曲行为分析*

张晓晴，欧智成

(华南理工大学土木与交通学院，广东 广州510640)

可变形电子技术在微电子、生物、医学等领域有广阔的应用前景［1］，它以硬质薄膜、柔性基底结构为基础，将薄膜粘附在已施加预应变的基底上，然后释放预应变，致使薄膜发生屈曲［2］。将薄膜/基底结构的屈曲特性应用于半导体纳米技术中，便可实现电子元件的可变形特性。R.Huang 等［3-6］建立了薄膜基底结构的力学模型，研究了各向同性、正交各向异性的弹性薄膜在弹性、粘性和粘弹性基底上的屈曲行为，得到了薄膜屈曲的波长、波幅和临界荷载等。B.Audolya 等［7］、X.Chen 等［8］、J.Song 等［9］研究了包括人字形、棋盘形、波浪形等多种受到双轴预应变荷载的薄膜屈曲构型。文献［10-12］中研究了有限窄带薄膜的屈曲，并考虑了大变形和超弹性的情况。

当前的研究主要集中在静力屈曲方面，并未考虑结构的动力响应，事实上无论是在生产还是使用过程中，可变形电子元件都不可避免地会承受各种动力荷载的作用。这些荷载可能来自化学反应、机械碰撞、环境温度等，并最终体现在薄膜/基底结构受到的随时间变化的荷载。一般而言，这些荷载包括线性荷载、阶跃荷载、脉冲荷载、周期荷载和随动荷载等，原来的静力屈曲问题转化为与时间相关的动力屈曲问题。动力屈曲同静力屈曲分析一样，需要确定临界荷载和屈曲模态等，但动力屈曲有更丰富的动力响应，包括冲击屈曲、振荡屈曲等，而且对初始条件敏感［13-14］。

本文中，分析线性荷载下薄膜/基底结构的动力屈曲。假设薄膜受到线性递增的单轴预应变，利用Kirchhoff 平板理论描述薄膜，用小变形平面应变理论描述基底，导出薄膜的应变能和动能，以及基底对薄膜所作的功。然后定义Lagrange 函数，利用Euler-Lagrange 方程导出动力屈曲控制方程。通过量纲一化后，得到一个关于屈曲波幅和线性荷载的非线性常微分方程。通过数值方法求解结构的动力响应，并利用B-R 准则确定临界屈曲荷载［15］，最后讨论初始条件对动力响应的影响。可以发现，动力屈曲的临界荷载较静力屈曲的大，波幅响应围绕静力屈曲的振荡。

1 基本模型和控制方程

弹性薄膜无滑移地粘附在弹性基底上，薄膜厚度为h，基底厚度为H，且H≫h。基底受到单轴预拉伸应变ε0，以此时的构型为初始构型，以接触面的中心为原点建立坐标系，如图1(a)所示。释放基底的预应变，结构发生屈曲，如图1(b)所示，假设在此过程中薄膜受到线性变化的压缩应变ε(t)。用Kirchhoff 平板理论描述薄膜，用小变形理论描述基底。由于结构在y 方向的长度远大于波长，因此基底可简化为平面应变问题。薄膜与基底接触面处(z=0)的位移连续，基底底部固定，即边界条件为

式中:上标s 表示基底。

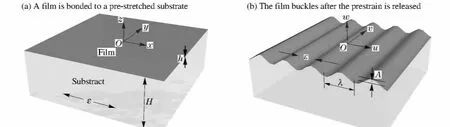
图1 硬质薄膜/柔性基底结构Fig.1 The structure in a stiff thin film bonded to a compliant thick substrate

1.1 薄膜

由于薄膜只受到单轴荷载，其基本方程可简化为一维情况，并考虑中等应变

式中:u0和w0分别表示薄膜中面上的面内位移和挠度。Kirchhoff 平板理论认为薄膜挠度沿着厚度方向无变化，等于中面挠度。但面内位移沿着厚度线性分布。于是薄膜任意位置的位移为

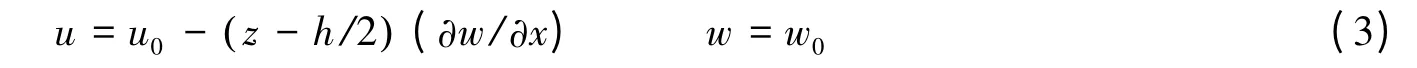
运用Hooke 定律得到薄膜中面的应力

将式(2)～(4)代入式(5)，得到位移表示的平衡方程

假设薄膜的挠度

式中:A(t)为波幅，k 为波数。假设薄膜的波长与时间无关，并且远大于厚度，λ=2π/k≫h，即kh≪1。将式(7)代入式(6)解得中面位移

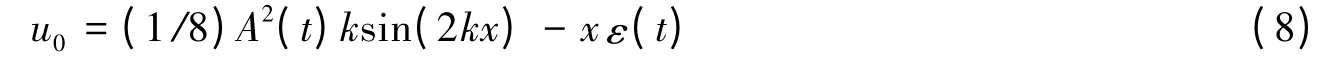
于是接触面处的位移

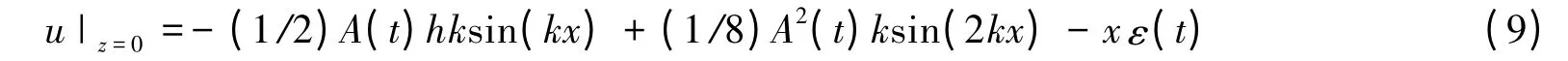
再由式(2)得薄膜的面内应变

薄膜的应变能包括弯曲应变能Ub和压缩应变能Um，即

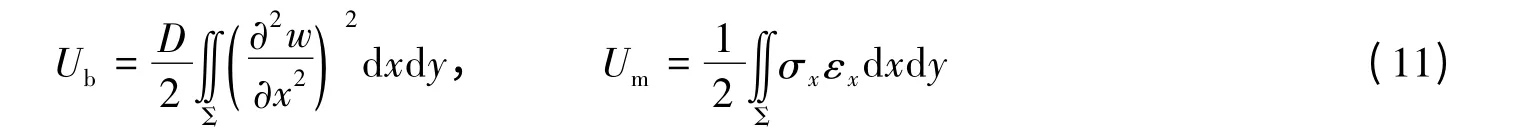
本文中，上标“·”表示对时间的一阶导数。

1.2 基底

计算基底对薄膜的反力。由小变形平面应变理论得基底应变

运用Hooke 定律(平面应变)得到应力

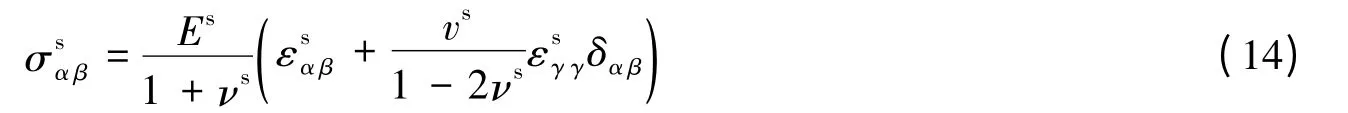
式中:Es和νs为基底的杨氏模量和泊松比。利用平衡方程

将式(13)～(14)代入式(15)，得到位移表示的平衡方程

分离变量得到

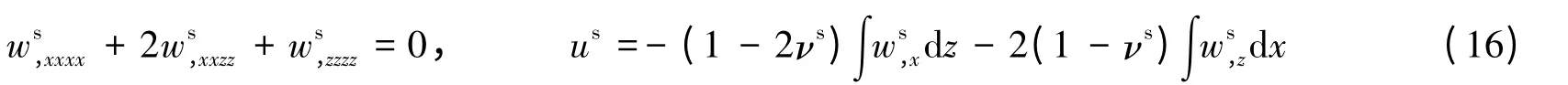
式中:下标“，”表示对坐标的偏导数。考虑位移的周期性和有界性，得到微分方程的通解为

利用边界条件(1)解得

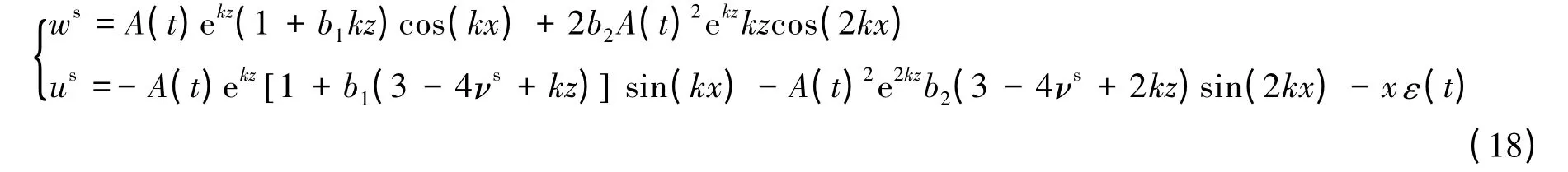
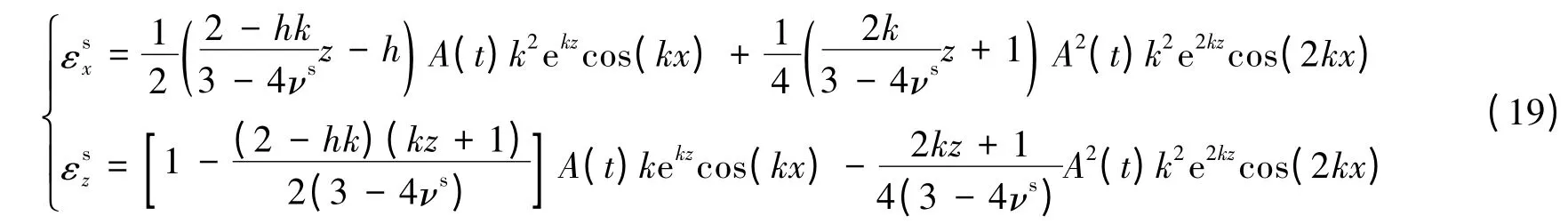
注意到基底的预应变ε0被完全释放。再式(19)代入式(14)，得到接触面上的应力

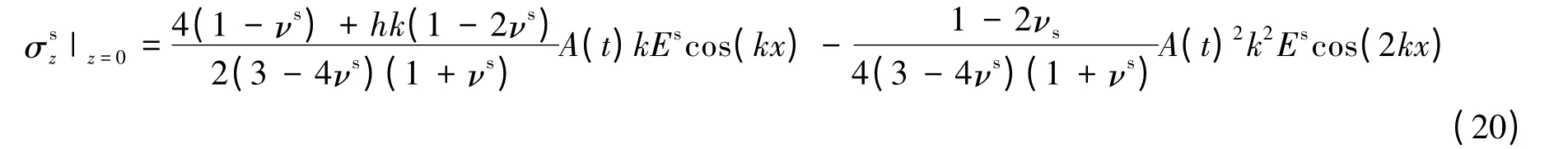
忽略高阶项和小量后得到基底对薄膜的作用力

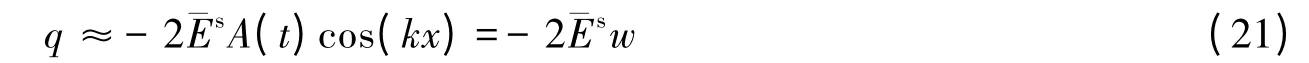
1.3 动力屈曲控制方程

定义Lagrange 函数

式中:薄膜应变能Ue=Ub+Um。将式(11)～(12)、(22)代入，得

考虑挠度的周期性，将式(7)、(10)代入式(24)，计算一个周期内的平均值，得到

将式(25)代入，整理得到

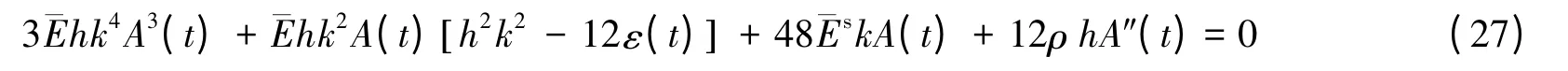
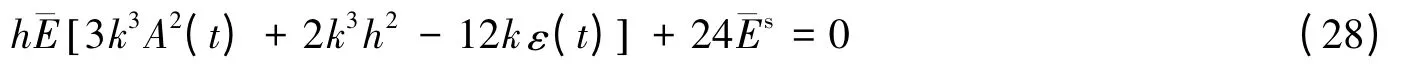
忽略式(27)中的惯性项12ρ hA″(t)，则得到静力屈曲的控制方程。联立式(28)解得静力屈曲时的平衡波数

将式(29)代入式(28)并令A=0，解得静力屈曲的临界荷载(预应变)

假设薄膜动力屈曲中平衡波数不变，把式(29)代入式(27)得到

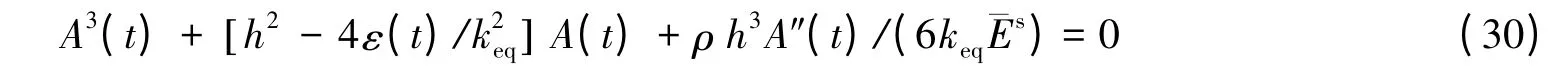
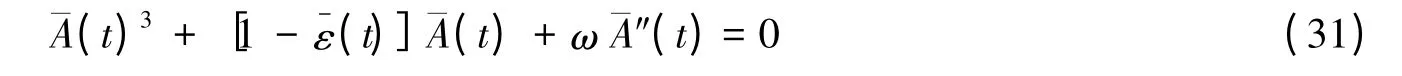
其中

2 动力屈曲

假设单位预应变随时间增长如下

式中:c 为变形率;τ 有两重意义，一为量纲一时间，二为当前应变较静力屈曲临界应变的相对增量。将式(33)代入式(31)得到线性荷载下的动力平衡微分方程为，或写成

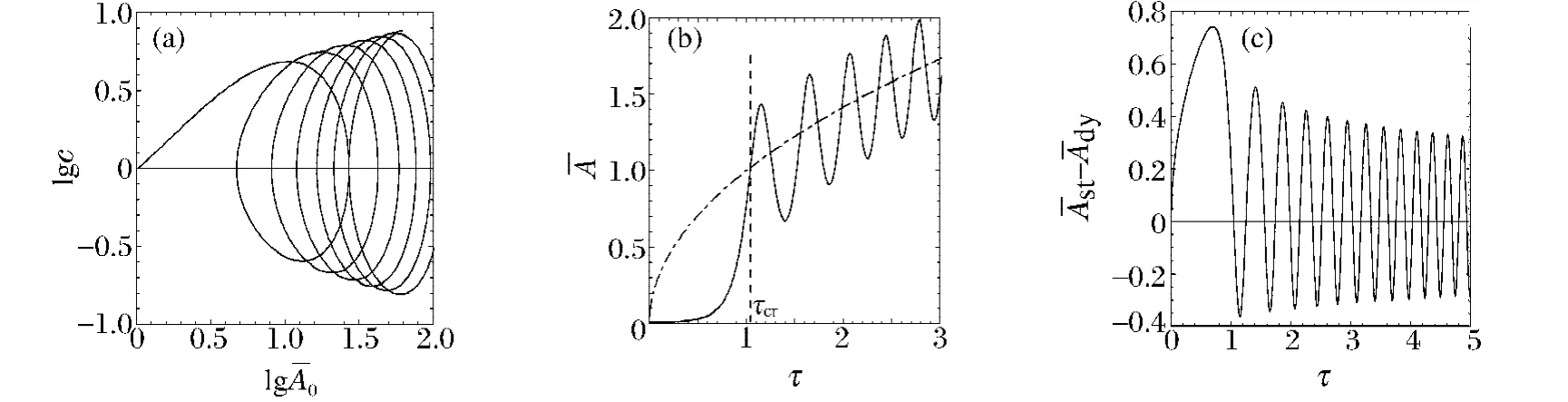
图2 动力响应Fig.2 Dynamic response

利用B-R 准则确定动力屈曲临界荷载［15］，即波幅响应第1 个拐点处。由式(34)得到临界荷载满足，即动力屈曲的临界荷载为动力屈曲与静力屈曲波幅响应的交点。由图2(b)～(c)可知，在动力波幅的第1 个极值点处，动力屈曲的波幅对静力屈曲的波幅的增幅最大，之后随着荷载的增大，增幅减小。定义动力屈曲波幅增长系数，表示第1 个极大值处二者的比值。

3 讨 论

图3 动力屈曲临界荷载Fig.3 The critical load in dynamic buckling

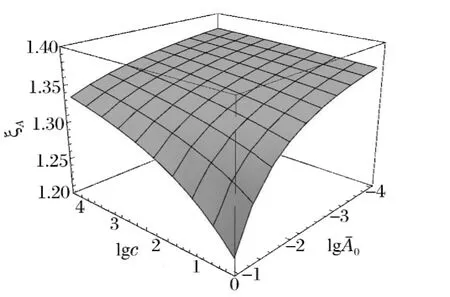
图4 动力屈曲波幅增长系数与初始挠度和应变率的关系Fig.4 The relationship among the increment ratio of dynamic buckling amplitude，initial amplitude and strain rate

4 结 论

基于Kirchhoff 平板理论以及Euler-Lagrange 方程导出薄膜、基底结构的动力屈曲控制方程，分析该结构在线性荷载下的动力特性。随着线性荷载的增大，波幅的动力响应先是缓慢增长，然后发生突变，最后围绕静力屈曲的路径振荡，并且波幅的峰值较静力屈曲的要大。动力屈曲受到初始挠度和应变率的影响，应变率越大，初始挠度越小，则临界荷载以及动力屈曲的波幅增幅也越大。当柔性电子元件受到的荷载较大时，结构可能发生二次屈曲，文中对基底的小变形假设也不再适用。

［1］ Wong W S，Salleo A.Flexible electronics:Materials and applications［M］.New York:Springer，2009.

［2］ Khang D Y，Jing H Q，Huang Y，et al.A stretchable form of single-crystal silicon for high-performance electronics on rubber substrates［J］.Science，2006，311(5758):208-212.

［3］ Huang R，Suo Z.Instability of a compressed elastic film on a viscous layer［J］.International Journal of Solids and Structures，2002，39(7):1791-1802.

［4］ Huang R.Kinetic wrinkling of an elastic film on a viscoelastic substrate［J］.Journal of the Mechanics and Physics of Solids，2005，53(1):63-89.

［5］ Im S H，Huang R.Evolution of wrinkles in elastic-viscoelastic bilayer thin films［J］.Journal of Applied Mechanics，2005，72(6):955-961.

［6］ Im S H，Huang R.Wrinkle patterns of anisotropic crystal films on viscoelastic substrates［J］.Journal of the Mechanics and Physics of Solids，2008，56(12):3315-3330.

［7］ Audoly B，Boudaoud A.Buckling of a stiff film bound to a compliant substrate－Part I:Formulation，linear stability of cylindrical patterns，secondary bifurcations［J］.Journal of the Mechanics and Physics of Solids，2008，56(7):2401-2421.

［8］ Chen X，Hutchinson J W.Herringbone buckling patterns of compressed thin films on compliant substrates［J］.Journal of Applied Mechanics，2004，71(5):597-603.

［9］ Song J，Jiang H，Choi W M，et al.An analytical study of two-dimensional buckling of thin films on compliant substrates［J］.Journal of Applied Physics，2008，103(1):014303.

［10］ Jiang H Q，Khang D Y，Fei H Y，et al.Finite width effect of thin-films buckling on compliant substrate:Experimental and theoretical studies［J］.Journal of the Mechanics and Physics of Solids，2008，56(8):2585-2598.

［11］ Song J，Jiang H，Liu Z J，et al.Buckling of a stiff thin film on a compliant substrate in large deformation［J］.International Journal of Solids and Structures，2008，45(10):3107-3121.

［12］ Sun Y G，Choi W M，Jiang H Q，et al.Controlled buckling of semiconductor nanoribbons for stretchable electronics［J］.Nature Nanotechnology，2006，1(3):201-207.

［13］ Bolotin V V.The dynamic stability of elastic systems［M］.San Francisco:Holden-Day，1964.

［14］ Lindberg H E，Florence A L.Dynamic pulse buckling:Theory and experiment［M］.Dordrecht:Martinus Nijhoff，1987.

［15］ Budiansky B，Roth R S.Axisymmetric dynamic buckling of clamped shallow spherical shells［J］.NASA Technical Note，1962:597-606.

［16］ Huang H，Han Q.Nonlinear dynamic buckling of functionally graded cylindrical shells subjected to time-dependent axial load［J］.Composite Structures，2010，92(2):593-598.