橡胶复合靶板抗射流侵彻的理论和实验研究*

祖旭东，黄正祥，贾 鑫

(南京理工大学智能弹药国防重点学科实验室，江苏 南京210094)

橡胶复合材料具有密度低、比强度和比模量高、断裂安全性好、可设计性强和制作工艺良好等优点，在坦克、步兵战车和舰船的防护领域应用广泛［1］，对橡胶复合材料抗弹性能的研究主要集中在抗枪弹、榴弹破片和动能弹等方面。橡胶复合靶板抗射流侵彻机理目前主要是依据爆炸反应装甲抗射流侵彻理论，从飞板干扰射流稳定性方面分析。A.Helte 等［2］将橡胶复合装甲中的橡胶作为一种惰性炸药，认为射流侵彻橡胶复合靶板时，复合靶板中的橡胶夹层发生爆炸(或汽化)，使得金属面板和背板出现沿法线背离橡胶夹层方向的速度，橡胶复合靶板对射流的干扰与爆炸反应装甲对射流的干扰机理相似，认为射流侵彻橡胶复合靶后射流的变形情况可以采用开尔文-亥姆霍兹不稳定性分析。

本文中，通过分析应力波对橡胶复合板靶板面板质点速度的影响，依据开尔文-亥姆霍兹不稳定性理论建立橡胶复合靶板对射流的干扰模型，分析倾角和橡胶夹层厚度对橡胶复合靶抗射流侵彻的影响，并通过穿深实验进行验证，指出橡胶复合靶板的最佳工作状态。

1 橡胶复合靶板抗射流侵彻理论模型

1.1 基本现象描述

橡胶复合靶板实际上是由2 块金属薄板和1 块橡胶板通过黏合剂粘结组成的系统。图1 是橡胶复合靶干扰射流的示意图。当成型装药射流侵彻橡胶复合靶板时，橡胶夹层材料与射流相互作用，橡胶复合靶板干扰特定速度区间内射流微元的稳定，使得射流出现周期性的变形和断裂。为了方便讨论，把橡胶复合靶板外法线方向与射流运动方向之间的最小夹角小于π/2 的金属板称为前板(F 板)，与射流运动方向之间夹角大于π/2 的金属板称为后板(B 板)。

1.2 射流侵彻橡胶复合靶板过程分析

射流侵彻橡胶复合靶过程分为4 个阶段。第1 阶段，自射流侵彻橡胶复合靶开始至射流穿透橡胶复合靶板结束，连续射流定常侵彻橡胶复合靶。第2 阶段，自射流穿透橡胶复合靶至橡胶复合靶板盖板由于应力波作用产生沿法线方向的质点速度结束，橡胶复合靶板对射流无干扰作用，射流的变形、断裂情况与射流在空气中的运动情况相同。第3 阶段，自橡胶复合靶盖板由于应力波的作用产生沿法线方向的质点速度开始至射流被橡胶复合靶干扰的最小速度结束，该阶段橡胶复合靶板与射流发生周期性作用，干扰射流的稳定性。射流与橡胶复合靶作用时即发生断裂，射流剩余侵彻能力按断裂射流计算。断裂时间按各个周期内射流与橡胶复合板接触时间计算。第4 阶段，自射流被橡胶复合靶干扰的最小速度至射流尾部，该阶段射流受到较小扰动，变形较小，为简化分析、计算，忽略微小变形，按连续射流在空气中运动情况分析。

图1 橡胶复合靶板对射流干扰示意图Fig.1 Sketch of rubber composite armor disturb the stabilities of shape charge jet

为准确分析橡胶复合靶板对射流的干扰情况，采用射流连续侵彻模型，考虑射流头尾速度、速度梯度和射流直径等参数对橡胶复合靶板抗射流侵彻性能的影响。

1.3 射流定常侵彻橡胶复合靶

射流侵彻橡胶复合靶板第1 阶段:射流侵彻橡胶复合靶板，射流无明显被干扰阶段。在该阶段射流侵彻橡胶复合靶板时，橡胶复合靶板的背板和面板会在碰撞点形成一个膨胀孔，孔径不断增大，背板和面板上开孔的质点速度不断变化。然而此阶段，复合靶板和射流作用产生的应力波还没有作用到面板和背板上，面板和背板还没有沿法线方向的速度。此时面板和背板未与射流发生切割、干扰作用，因此该阶段仅考虑射流定常侵彻复合靶板情况。

1.4 橡胶复合靶板对射流无干扰阶段

该阶段为射流穿透橡胶复合靶板至应力波传播到橡胶复合靶板背板，此阶段，橡胶复合靶板对射流无明显干扰作用。

1.4.1 橡胶复合靶板面板质点速度计算

为便于分析，将射流作为准定常不可压流体［3］进行研究。

射流侵彻复合靶板过程中射流速度衰减及应力波传播的几点假设:(1)忽略射流侵彻复合靶板过程中复合靶板强度的影响;(2)应力波在橡胶复合靶中以平面波形式传播;(3)由于钢的波阻抗是橡胶波阻抗的100 倍以上，因此忽略应力波在钢板中的衰减，仅考虑应力波在橡胶中的衰减。

当射流侵彻复合靶板开坑时(见图2)，根据伯努利方程可得点A1 处靶板上物质点的速度

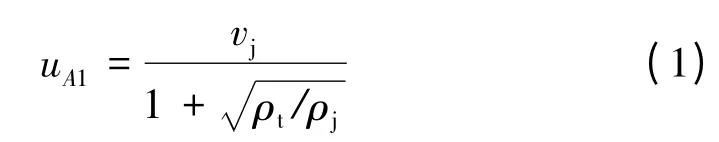
式中:vj为射流速度，ρt、ρj分别为靶板和射流的密度。

根据应力波原理，透射波系数和反射波系数分别为

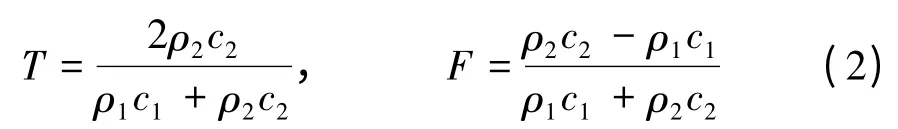
式中:ρ1c1，ρ2c2分别为入射介质和传入介质的波阻抗。

橡胶属于粘弹性材料，在粘弹性介质中由于粘性效应，应 力 波 的 衰 减 可 以 用 指 数 函 数e－γδp表 示。其中γ=γ(ω)为材料的传播系数，ω 为角频率，δp为材料厚度，可由霍普金森杆实验测定［4］。根据费马原理，应力波是沿着所需时间为极小值的路径传播的。

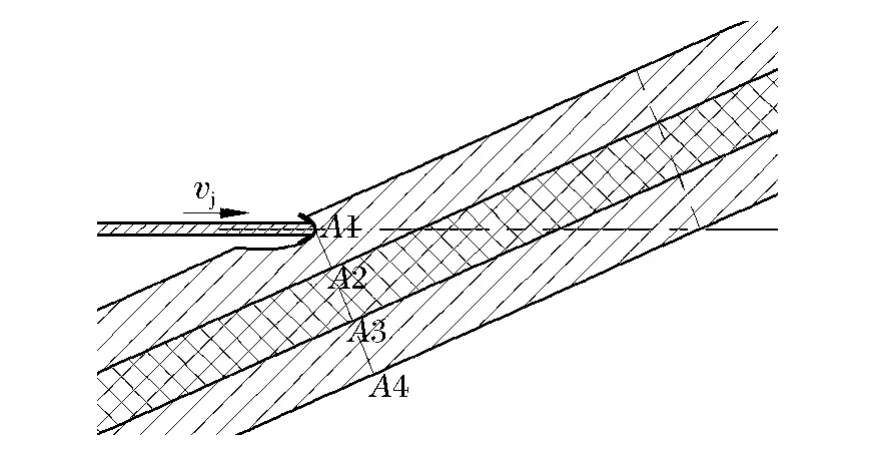
图2 射流侵彻橡胶复合靶板示意图Fig.2 Schematic diagram of jet penetration rubber composite armor

因此当波由背板传播到面板表面时，面板表面处的质点速度为

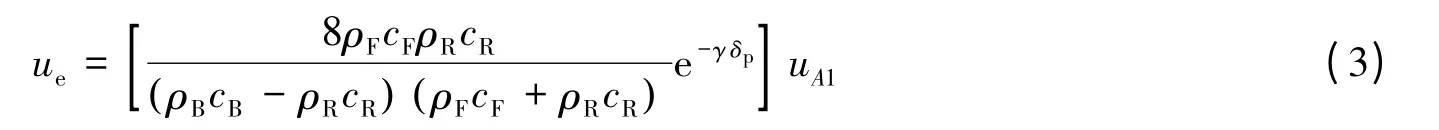
式中:下标B、F、R 分别表示背板、面板和橡胶夹层。

上述情况仅考虑了应力波在复合靶板中传播一次的过程。实际情况中，由于射流与橡胶复合靶板面板、背板的作用时间很短，应力波从产生到传播至背板的时间略小于射流侵彻复合靶板的时间，因此在考虑应力波对面板、背板质点速度的影响时不考虑应力波在面板、背板之间的反射作用。

根据上面的分析可知，橡胶复合靶板面板、背板的质点速度与橡胶复合靶板各层的材料的声速及应力波衰减速率有关。由于本文中研究的橡胶复合靶板为薄靶板，因此在计算过程中可以忽略应力波在金属板中的衰减。而橡胶中应力波衰减速率较大，因而只考虑应力波在橡胶夹层中的衰减。

1.4.2 未干扰段射流的剩余侵彻能力

为更加直观地表述橡胶复合靶对射流的干扰作用，通过射流侵彻橡胶复合靶板后的剩余穿深描述橡胶复合靶抗射流侵彻能力。成型装药采用口径56 mm 的基准成型装药，在橡胶复合靶后250 mm 处设置后效靶，见图3。

由于后效靶设置位置距离成型装药330 mm(5.9 倍装药口径)，大于成型装药的最佳炸高，因此考虑炸高对穿深的影响。

对于未被干扰部分射流，其侵彻能力根据虚拟原点法进行计算

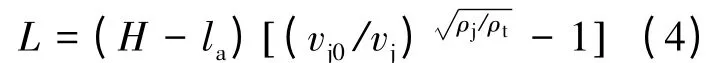
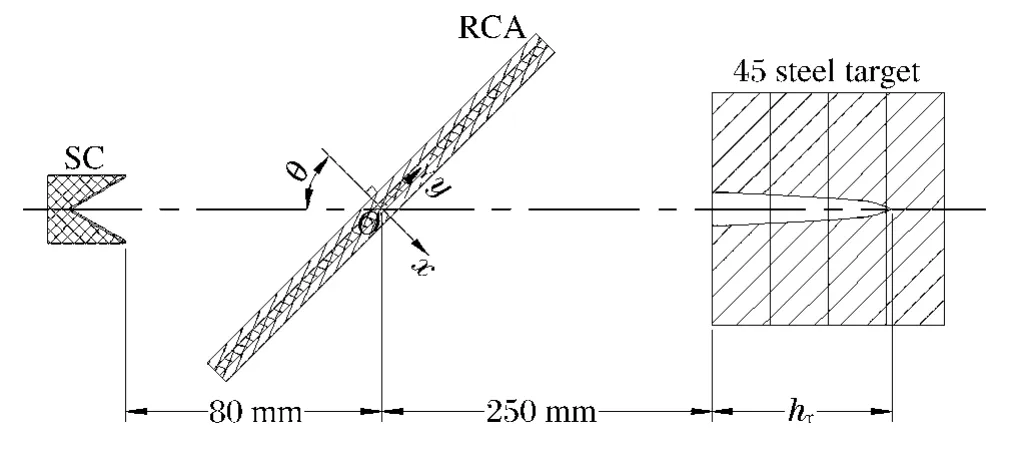
图3 弹靶关系简图Fig.3 Sketch of target and shaped charge setup

式中:L 为破甲深度，H 为炸高，la为药型罩顶点至药型罩底部的距离，vj0、vj分别为射流头部速度和射流尾部速度，ρj、ρt分别为射流和靶板的密度。

根据分析结果，对未干扰部分射流的侵彻能力进行修正如下

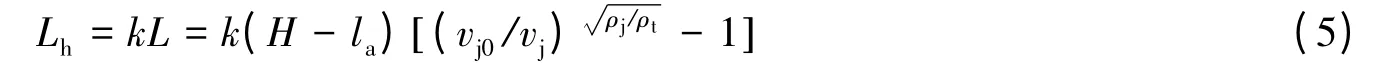
式中:k 为与炸高及橡胶复合靶板状态相关的因数，0＜k＜1。

1.5 橡胶复合靶对射流干扰阶段

1.5.1 橡胶复合靶板对射流干扰速度区间计算

由于橡胶夹层的存在使得射流侵彻橡胶复合靶时，面板和背板在应力波的作用下产生沿法线方向的速度，对射流形成横向切割，干扰射流的稳定性，导致射流发生变形和断裂。由于橡胶复合靶板不同于爆炸反应装甲，面板和背板的运动距离有一定限制，因此橡胶复合靶板面板、背板运动仅会对一部分射流段进行干扰，其干扰长度可由普朗特流体力学中的开尔文-亥姆霍兹不稳定性［5］计算得到。

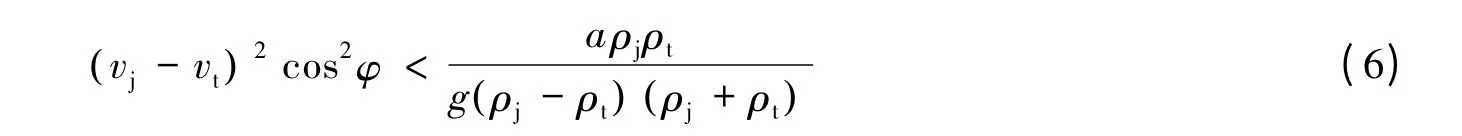
式中:a 为波矢，沿射流运动方向传播，a=2π/λ(rad/m)，a 随着雷诺数Red的减小即摩擦因数的减小而减小;λ 为射流微元被橡胶复合靶板干扰产生的振动波的波长;vj、vt为分别为射流和复合靶板背板运动速度，vt=ue;g 为重力加速度;φ 为波矢a 与速度v=vj－vt之间的夹角，φ=π/2－θ/2，其中θ 为射流与靶板外法线方向的夹角。

弹靶材料确定以后射流的不稳定特性只与射流速度vj、复合靶板背板速度vt以及夹角α 有关。

1.5.2 射流侵彻橡胶复合靶板后断裂周期［6］

射流侵彻橡胶复合靶板时，面板和背板的扩孔孔径随时间变化情况可由下式表达

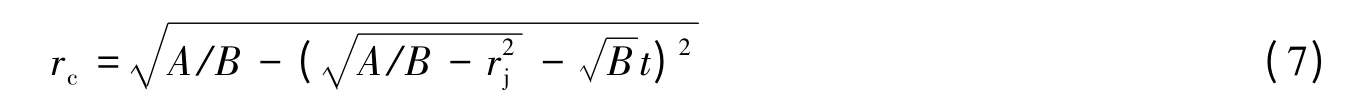
式中:rc为开孔半径;其中Rt为板的动态强度，vj为应力波传到面板时射流的速度;rj为射流传到面板时射流的直径。

为简化橡胶复合靶板对射流的干扰周期模型，作下述假设:(1)橡胶复合靶板背板、面板速度保持恒定不变;(2)射流上某微元被橡胶复合靶板面板干扰后，其微元扰动不会引起相邻微元的状态变化。

根据式(3)可计算出橡胶复合靶板面板、背板与射流作用区域的速度uF。在面板孔边缘点F，建立如图4 所示的坐标系，则点F 即面板的运动轨迹为

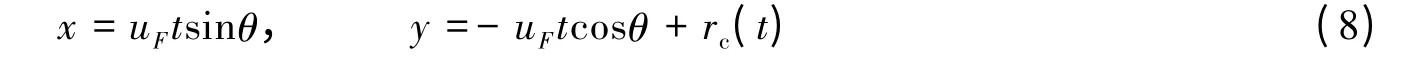
式(8)消去t，并结合式(7)得

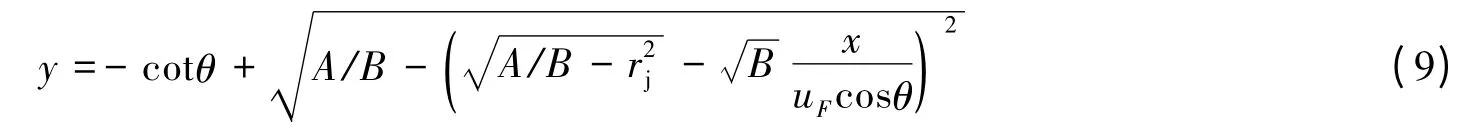
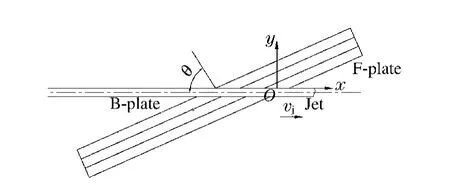
图4 橡胶复合靶板干扰射流频率计算模型Fig.4 Physical model of interaction frequency between surfaces plates of rubber composite armor and shaped charge jet

令y=0，可求得孔边缘与射流下一次作用时的距离，结合式(7)得

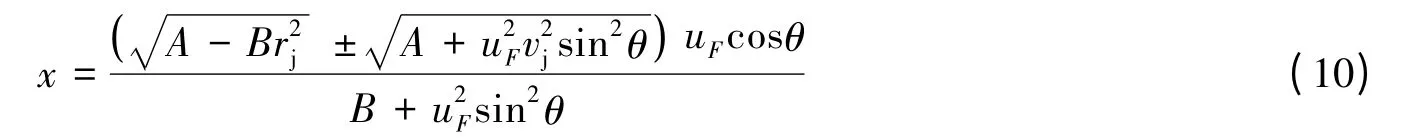
由于x 与uFcosθ 方向一致，因此式(10)中取“+”号，此点到下一干扰点的时间间隙

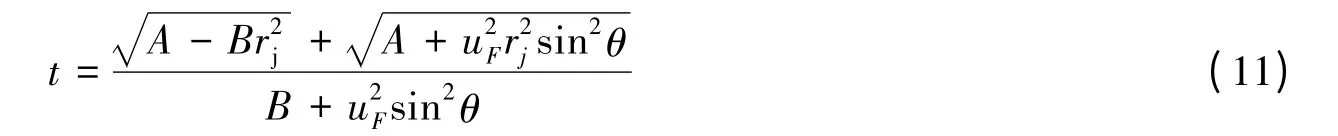
在此后的作用过程中，此过程反复出现，从而形成对射流的断续干扰。

为简化计算，认为橡胶复合靶板面板干扰射流时起作用长度为面板厚度。由于橡胶复合靶板对射流的作用力远大于射流微元之间的内应力，因此认为射流与橡胶复合靶作用时射流已发生变形、断裂。

1.5.3 断裂射流侵彻能力

对于被橡胶复合靶板面板质点速度干扰的射流部分，射流出现向橡胶复合靶板面板法线方向凸起的变形，且射流出现明显的断裂。出现变形的射流微元对后效靶的主穿深没有贡献，因此可以忽略其侵彻能力，而对于未偏离原射流运动轨迹的射流微元，考虑射流断裂对穿深的影响。

为简化起见，在计算中做以下假设:(1)射流与橡胶复合靶板作用后，残余射流的轴向速度和速度梯度不发生变化;忽略变形部分射流对后效靶侵彻深度的贡献。(2)通过橡胶复合靶板的射流微元仍为圆柱形，对后效靶靶板侵彻体积也为圆柱形。

对于断裂后的射流，认为其总长度不变，忽略割断之间的距离和射流偏移及反转，按照断裂射流侵彻计算公式并考虑炸高影响，有

式中:Lh为有橡胶复合装甲的破甲穿深，L(i)为射流微元穿过橡胶复合靶板后的长度，k′为炸高影响因数，0＜k′＜1。

1.6 射流尾部未被干扰部分

当射流微元速度低于射流被橡胶复合靶板干扰的最低干扰速度时，橡胶复合靶对射流无明显干扰作用，认为射流不因橡胶复合靶的存在而产生变形、断裂。射流剩余侵彻能力计算与第2 阶段相同。

1.7 橡胶复合靶板防护能力计算

由于橡胶复合靶板状态不同，因此剩余穿深不能直接作为评定橡胶复合靶板防护能力的标准。采用空间防护因数Es，质量防护因数Em和差分防护因数Δec来表示复合装甲的防护能力。质量防护因数Em描述复合靶的整体抗侵彻能力，空间防护因数Es描述装甲钢板与橡胶复合靶板的等价侵彻深度比，差分防护因数Δec描述材料本身所表现出来的抗侵彻性能［7］

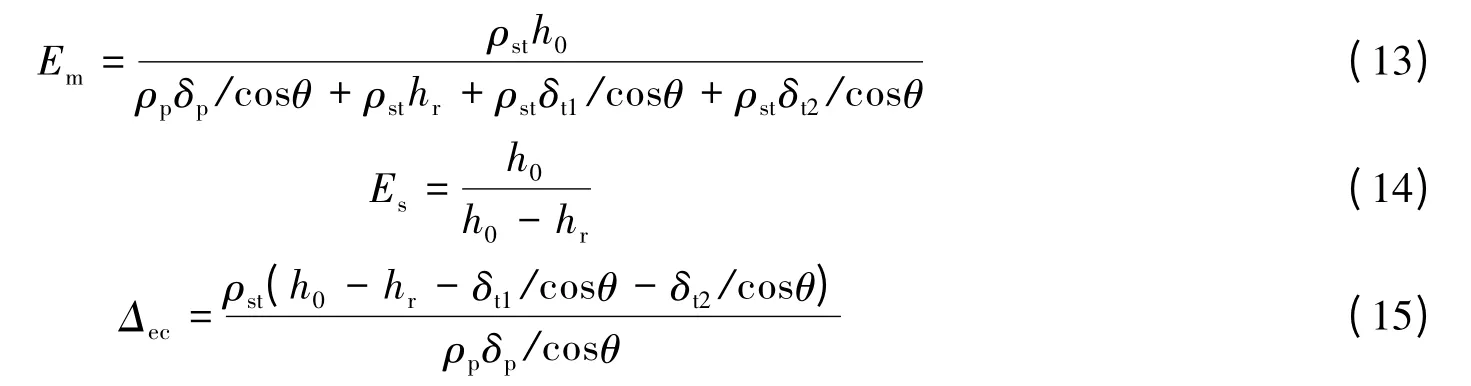
式中:ρst为钢的密度，ρp为复合靶夹层密度，h0为Ø56 mm 标准聚能装药基准穿深，hr为射流侵彻橡胶复合靶板后的剩余穿深，δt1为复合靶面板厚度，δt2为复合靶底板厚度，δp为复合靶夹层厚度。可计算出橡胶复合靶对射流的质量防护因数、空间防护因数和差分防护因数。

2 橡胶复合靶板抗射流侵彻实验

2.1 基准射流实验

为使研究具有普适性，采用的成型装药为直径56 mm 标准成型装药。标准成型装药药形罩采用锥形药形罩，药形罩材料为紫铜，装药直径为56 mm，无壳体装药，锥形药形罩壁厚为0.8 mm，炸药量203 g。标准成型装药如图5 所示。标准成型装药炸高80 mm，用8#火雷管起爆，靶板为45 钢。在炸高筒的上部放置启动靶，下部放置停止靶，启动靶和停止靶采用铜箔，利用测时仪记录射流头部穿过两靶时间，测定标准成型装药头部速度。实验现场照片分别如图6 所示。

图5 标准成型装药Fig.5 Stander shaped charge

图6 成型装药性能测试装置Fig.6 Performance test devices of shaped charge

成型装药性能测试结果如表1 所示。结果表明所设计的标准成型装药在相同炸高条件下下，平均穿深为184 mm，相对误差为1%，用该穿深作为成型装药对半无限钢靶侵彻的基准穿深。入口直径和出口直径基本相同，射流一致性较好，满足基准成型装药技术指标要求。

根据基准成型装药X 射线照片及数值计算可知，射流尾部速度约1.9 km/s，头部直径为1.5 mm，尾部直径约9 mm，成型装药起爆30 μs 后射流长度约111.5 mm。

表1 成型装药性能测试结果Table 1 Results of shaped charge performance experiment

2.2 穿深实验条件

实验中使用的橡胶复合靶板尺寸为300 mm×150 mm，上下2 层靶板为Q235 钢板，厚3 mm，中间为橡胶夹层。Q235 钢板经过喷砂处理后与橡胶夹层通过黏合剂粘合在一起。成型装药(SC)与橡胶复合靶板(RCA)间通过炸高筒连接，炸高筒轴线距离为80 mm，橡胶复合靶板与射流中轴线夹角为22°，在橡胶复合靶板后设置后效靶(厚180 mm、直径100 mm 的Q235 钢靶)，后效靶距橡胶复合靶250 mm，弹靶位置如图3 所示，现场布置情况如图7 所示。橡胶复合靶板中橡胶夹层的厚度分别为2、3、5、8 mm。橡胶材料为天然橡胶，密度1.3 g/cm3，邵氏硬度75HA，拉伸强度20 MPa，最大伸长率400%，面板、背板材料为Q235 钢，后效靶材料为45 钢。

2.3 穿深实验结果及分析

2.3.1 不同橡胶夹层厚度橡胶复合靶抗射流侵彻性能

成型装药射流侵彻橡胶复合靶板后，射流出现不同程度的断裂、变形，在后效靶靶面形成多次开坑，后效靶靶面上开坑情况如图8 所示。

图7 弹靶布置情况Fig.7 Location of the rubber composite amour with the shaped charge

图8 不同橡胶夹层厚度情况下射流侵彻后效靶开坑情况Fig.8 Crater of the shaped charge jet penetrating the after effects target after the jet penetrated the rubber composite armor of which the thickness of sandwich rubber changed

不同橡胶夹层材料厚度情况下成型装药射流侵彻橡胶复合靶板后的剩余侵彻深度、质量防护因数Em，空间防护因数Es和差分防护因数Δec如图9 ～10 所示。

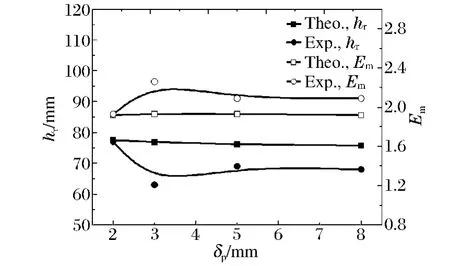
图9 橡胶夹层厚度与剩余穿深和质量防护因数的关系Fig.9 Relationship between surplus depth，quality defense coefficient and the thickness of rubber

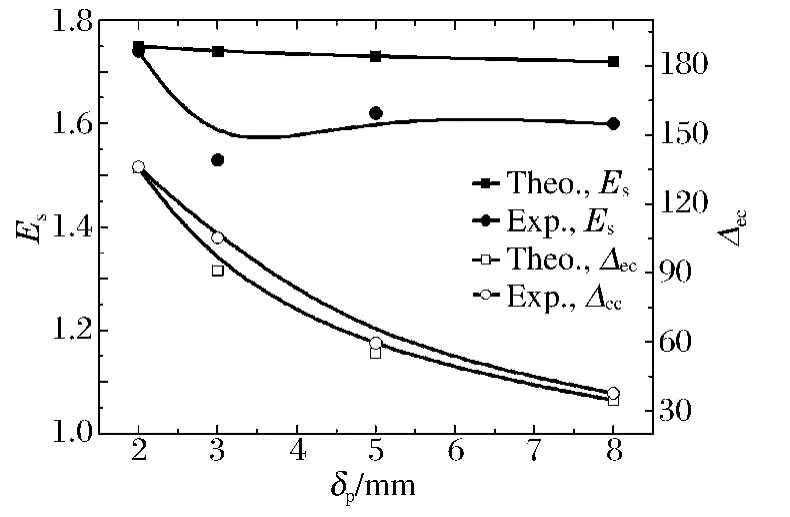
图10 橡胶夹层厚度与空间防护因数和差分防护因数的关系Fig.10 Relationship between space defense coefficient，differential defense coefficient and the thickness of rubber

由图9 ～10 可知，随着橡胶夹层厚度的增加，橡胶复合靶板的差分防护因数降低，即橡胶材料在橡胶复合靶板中的作用降低。对于射流的剩余穿深、橡胶复合靶板的质量防护因数和空间防护因数，理论计算结果与实验结果都有一定的差别，实验结果小于理论计算结果，原因可能有以下几点:(1)在分析橡胶复合靶板对射流的干扰作用时，仅考虑了橡胶复合靶板面板、背板材料密度及声速对射流干扰的作用，未考虑橡胶复合靶板整体结构效应的影响;(2)忽略了射流侵彻橡胶过程中橡胶破碎颗粒对射流断裂的影响;(3)忽略了橡胶复合靶板背板对射流的干扰作用。橡胶复合靶板对射流的干扰作用主要集中在橡胶复合靶板的面板，但是橡胶复合靶板背板同样因为间隔效应对射流具有一定干扰作用，且厚度不同时其干扰大小不同;(4)理论分析中为考虑橡胶夹层和盖板的连接情况，忽略了靶板之间的连接对橡胶复合靶板抗射流干扰的影响;(5)理论分析计算中忽略了空气阻力对射流断裂的影响。

在分析计算过程中忽略了以上5 个因素，造成射流侵彻橡胶复合靶板后对其剩余穿深实验数值比理论计算结果偏小。与理论结果相比，实验所得剩余穿深误差在橡胶夹层为3 mm 时最大，约18.1%。在橡胶夹层厚度为2、5 和8 mm 时，误差分别为0.7%、10.3%和10.3%。

根据理论和实验结果可知，由于橡胶材料对应力波的衰减作用，使得随着橡胶材料厚度的增加复合靶板对射流的干扰能力降低。因此在保证橡胶复合靶板结构效应的情况下，橡胶夹层选择较小厚度。考虑复合靶的结构效应影响，橡胶夹层材料厚度为3 ～3.5 mm 时橡胶复合靶板具有最优的防护性能。

2.3.2 倾角变化时橡胶复合靶抗射流侵彻性能

橡胶复合靶板在不同倾角时，成型装药射流侵彻橡胶复合靶板后，射流出现不同程度的断裂、变形，后效靶钢锭上的开坑及穿深情况可以间接地体现，后效靶靶面上开坑情况如图11 所示。

图11 射流侵彻后效靶后射流弹坑情况Fig.11 Crater of the shaped charge jet penetrating the after effects target

橡胶复合靶板在不同倾角时，成型装药射流侵彻橡胶复合靶板后的剩余侵彻深度hr、质量防护因数Em、空间防护因数Es和差分防护因数Δec如图12 ～13 所示。

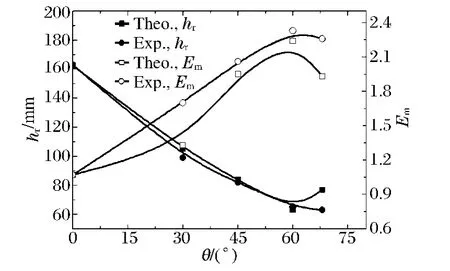
图12 倾角与剩余穿深和质量防护因数的关系Fig.12 Relationship between surplus depth，quality defense coefficient and the dip angle

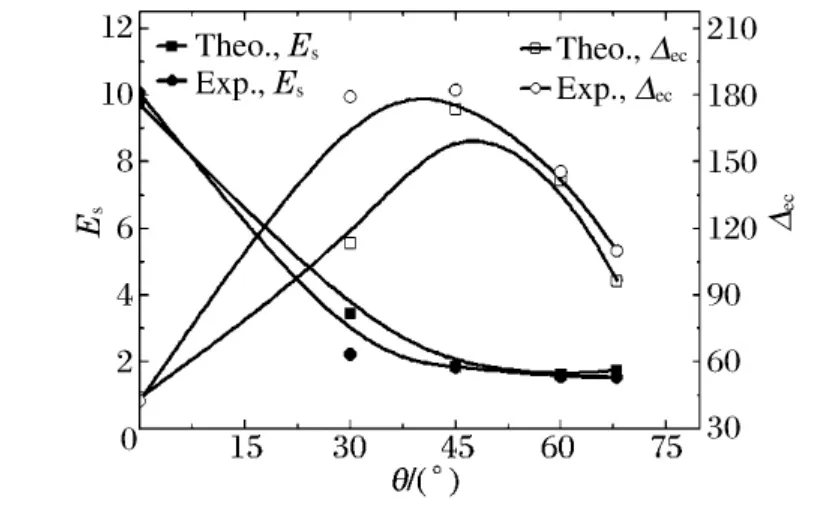
图13 倾角与空间防护因数和差分防护因数的关系Fig.13 Relationship between space defense coefficient，differential defense coefficient and the dip angle

由图12 ～13 可知，随着橡胶复合靶板倾角的增加，理论分析和实验结果变化一致，橡胶复合靶板的防护性能并不是单调递增的。在0°～60°范围，橡胶复合靶板随着倾角增加呈正效应，在60°～68°，橡胶复合靶板随着倾角的增加呈负效应。橡胶复合靶板的差分防护因数在30°～60°达到最大值，说明在此倾角范围内橡胶夹层材料在橡胶复合靶板中的作用最大。在60°～68°范围内，橡胶复合靶板的空间防护因数最小，且大小基本相等，说明该结构橡胶复合靶板在此倾角范围内空间防护效能最优。同时橡胶复合靶板的质量防护因数在60°左右时达到最大值，其质量防护能力最优。因此橡胶复合靶板在倾角为60°时具有最优的防护性能。

3 结 论

(1)由于应力波在橡胶夹层中传播时衰减较快，在满足结构要求时，随着橡胶夹层厚度的增加，橡胶复合靶板抗射流侵彻能力降低。根据理论计算和实验研究结果可知，在倾角为68°时，橡胶夹层的厚度为3 ～3.5 mm 时橡胶复合靶板具有最优的抗射流侵彻能力。

(2)倾角效应对橡胶复合靶板抗射流的侵彻性能影响较大，研究表明，所研究的橡胶复合靶板在倾角为60°时，橡胶复合靶板对射流的干扰能力最强。

(3)橡胶复合靶板具有优异的抗射流侵彻性能，可作为新型防护装甲。

［1］ 邵磊，余新泉，于良.防弹纤维复合材料在装甲防护上的应用［J］.高科技材料与应用，2007，32(2):31-34，45.SHAO Lei，YU Xin-quan，YU Liang.Applications of antiballistic fiber composites in armor protection［J］.Hi-Tech Fiber＆Application，2007，32(2):31-34，45.

［2］ Helte A，Lidén E.The role of Kelvin-Helmholtz instabilities on shaped charge jet interaction with reactive armours plates［J］.Journal of Applied Mechanics，2010，77(5):051805-1-051805-8.

［3］ 王树有.串联侵彻战斗部对钢筋混凝土介质的侵彻机理［D］.南京:南京理工大学，2006.

［4］ 刘孝敏，胡时胜，陈智.粘弹性Hopkinson 压杆中波的衰减和弥散［J］.固体力学学报，2002，23(1):81-86.LIU Xiao-min，HU Shi-sheng，CHEN Zhi.The wave propagation attenuation and dispersion in a viscoelastic Hopkinson pressure bar［J］.Acta Mechanica Solida Sinica，2002，23(1):81-86.

［5］ H.欧特尔.普朗特流体力学基础［M］.张自强，钱翼稷，李宗瑞，译.北京:科学出版社，2008.

［6］ 李如江，沈兆武.NATO 角和飞板速度对平板装药干扰射流频率的影响［J］.含能材料，2008，16(3):295-297，318.LI Ru-jiang，SHEN Zhao-wu.Effect of NATO angle and plate velocity on disturbance frequency of reactive armor against shaped charge jet［J］.Chinese Journal of Energetic Materials，2008，16(3):295-297，318.

［7］ 张自强，赵宝荣，张瑞生，等.装甲防护技术基础［M］.北京:兵器工业出版社，2000.