直线包络方法加工凸曲线回转工件的数学模型与效率研究

林彬，竹永奎，杜蕃，袁启海

(天津大学 先进陶瓷和加工技术教育部重点实验室，天津300072)

0 引言

近年来，随着经济的飞速发展，航空航天、军事领域也获得了较快的发展。凸曲线回转工件广泛应用于这些领域，并要求较高的精度和表面质量［1］。凸曲线回转工件的成形大多采用轨迹法，依靠带有圆弧的刀尖与加工表面以点接触的方式来磨削成形。普遍采用的加工刀具为平行砂轮，由于平行砂轮圆角半径较小，每次切削深度有限，加工效率很低。一些先进的陶瓷加工实验室利用较大圆角半径的杯形砂轮代替平行砂轮，改善了切削深度较小的问题，但是由于依靠砂轮刀尖圆弧来去除材料和保证工件的外形精度，当砂轮刀尖圆弧快速磨损以后，很难继续保证加工精度，所以这种方法仍然无法满足现代高效精密加工的需求。

文献［2］提出了一种将端面磨削应用到加工凸曲线回转工件的方法，通过不断改变砂轮回转轴线的角度使砂轮端面始终与工件相切，最后由砂轮端面包络出工件外形。从工件截面轮廓的几何形态可以看出，这种方法属于直线包络方法，但是文中没有给出符合这种加工方法成形机理的刀触点计算模型，不能用于实际加工。因此，研究直线包络方法的成型机理、推导出基于等残留高度的刀触点计算模型，对于凸曲线回转工件的实际磨削加工具有指导意义，而且对于改善精度，提高磨削效率也具有探索意义。

1 成型机理和实现方法

1.1 原理分析

如图1所示，轨迹成形方法是依靠刀尖处圆弧相对于工件以点位运动的方式磨削出工件轮廓，实际的加工轮廓为多条凹形轮廓带。两相邻凹形轮廓带与工件理想轮廓间的区域为残留区。它的最大高度为最大残留高度，是影响工件外形轮廓精度的主要因素。

如图2所示，直线包络法是依靠一组与工件截面轮廓相切的直线相对工件点位运动来包络出工件外形，实际的加工轮廓为多条锥形轮廓带。两相邻锥形轮廓带与工件实际轮廓间的区域为加工残留区。

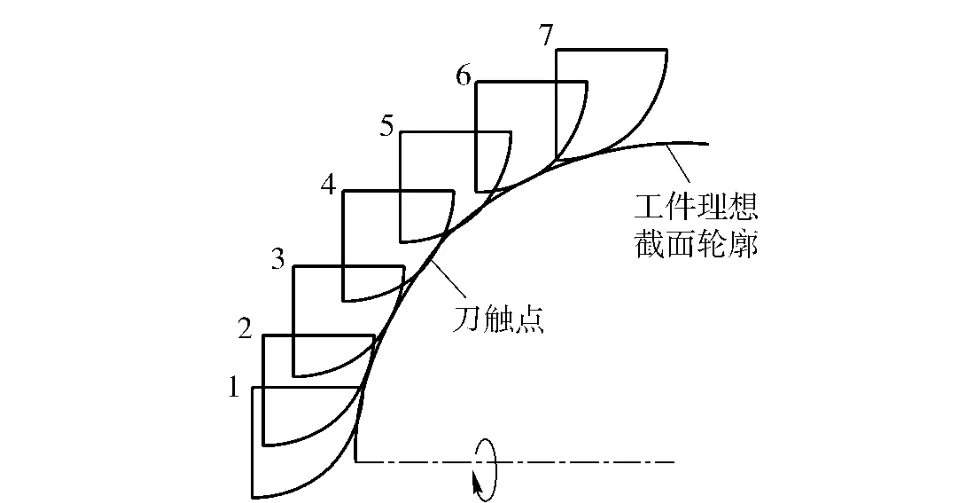
图1 轨迹法成型原理示意图Fig.1 Schematic diagram of method of loci

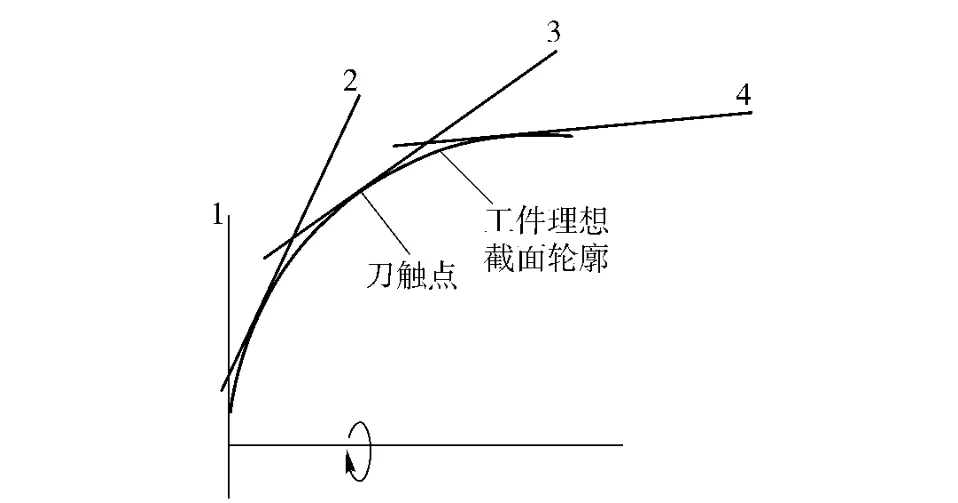
图2 直线包络法成型原理示意图Fig.2 Schematic diagram of lines enveloping method

1.2 实现方法

图3所示为利用杯形砂轮，采用轨迹成型方法磨削加工凸函数回转工件的运动原理图。加工中工件作回转运动，砂轮高速旋转，砂轮回转轴线角度保持不变，当砂轮进刀至一个刀位点时保持不动，工件回转进给，依靠砂轮周边圆弧进行磨削。工件完成一圈加工后，砂轮再运动到下一刀位点，加工工件下一圈。最终靠带有圆弧的刀尖与加工表面以点位运动的方式来磨削成形。

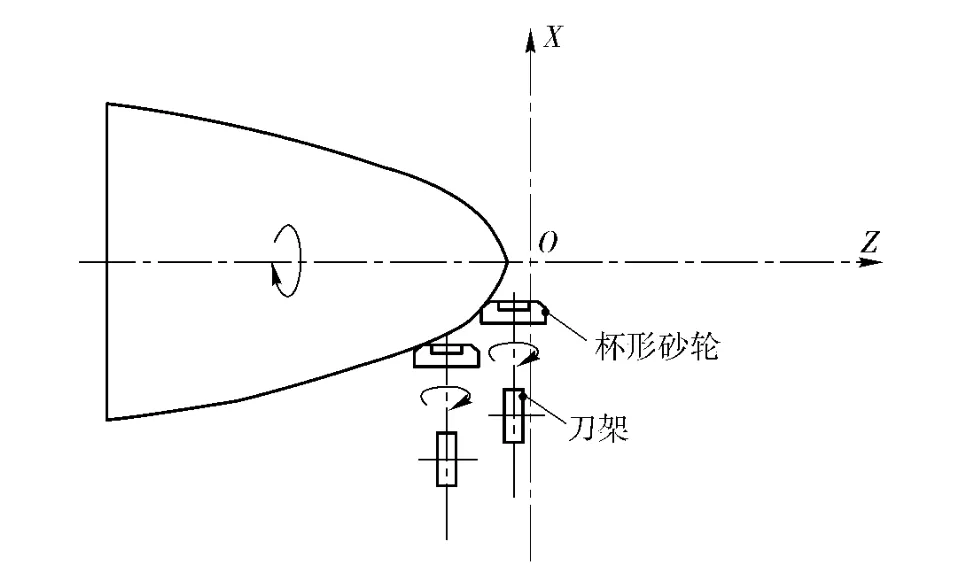
图3 杯形砂轮实现轨迹成形方法运动原理示意图Fig.3 Schematic diagram of using cup wheel to grind parts by method of loci

图4所示为利用杯形砂轮，采用直线包络成型方法磨削加工凸函数回转工件的运动原理图。与轨迹法不同的是选用砂轮端面上的任意半径圆弧(这个圆弧在截面上体现为一个点，如图4中的A 点)作为成形点，通过调整砂轮回转轴线的转角及位移使得砂轮底面始终与回转工件截面轮廓线在选定的成形点处相切，最终靠砂轮底面包络出工件外形［2］。这种加工方法在磨削过程中，砂轮进行的是端面磨削，与普通磨削相比，具备高效、高精度的特点。

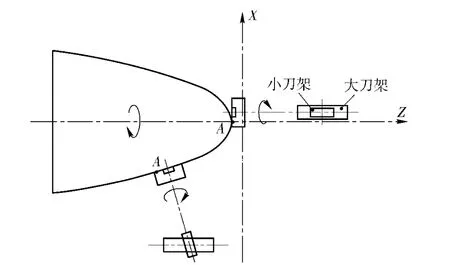
图4 杯形砂轮实现直线包络方法运动原理示意图Fig.4 Schematic diagram of using cup wheel to grind parts by lines enveloping method

图5所示为利用平行砂轮，采用直线包络成型方法磨削加工凸函数回转工件的运动原理图。与杯形砂轮不同的是选用平行砂轮外圆面上距离端面任意距离的圆弧(这个圆弧在截面上体现为一个点，如图5中的A 点)作为成形点，最终由砂轮外圆面包络出工件外形。这种加工方法在磨削过程中，可保证磨削区域的磨削速度相同，改善表面质量。

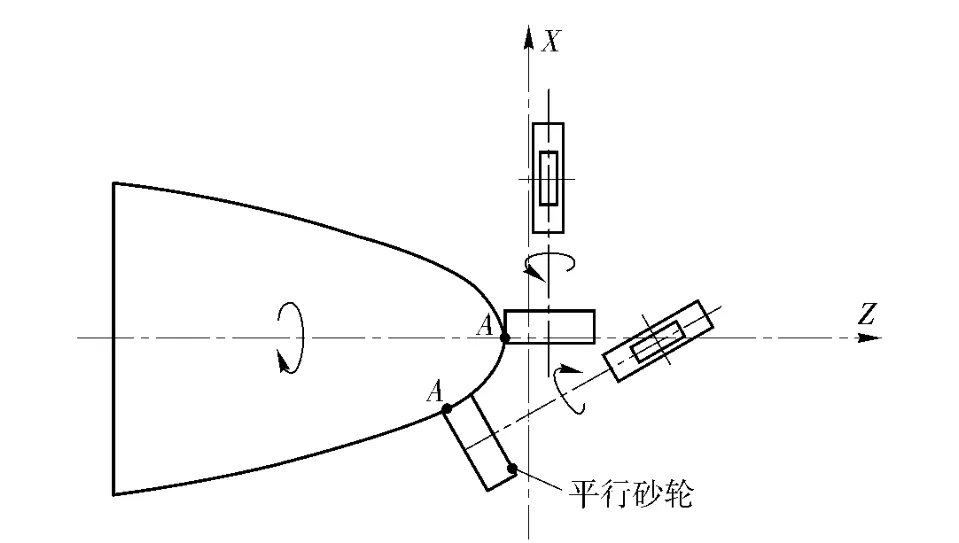
图5 平行砂轮实现直线包络方法运动原理示意图Fig.5 Schematic diagram of using parallel grinding wheel to grind parts by lines enveloping method

2 刀触点计算

图1与图2所示，圆弧或直线与工件截面凸曲线相切的实际位置都是由工件截面凸曲线上刀触点决定的，一个刀触点就决定一条加工带，而且两刀触点间的距离影响着残留区域的高度。现在应用比较广泛的刀触点计算方法主要有等步长法、等参数法和等残留高度法［3］。前两种方法计算简便，但是都存在重复切削的问题，影响加工效率。而基于等残留高度的刀触点计算方法不仅消除了重复切削，还可以人为控制残留高度的大小。

图6所示，A、B 是刀触点，OA 和OB 分别是过点A 和点B 与工件截面凸曲线相切的直线，它们代表了实际加工中，工件截面区域相邻刀触点A、B处，砂轮成型面(杯形砂轮是端面，平行砂轮是外圆面)与工件的接触情况。它们的交点O 到工件截面凸曲线的最大距离h 就是实际加工的残留高度。由于实际加工中步长相对较小，我们假设点A 和点B之间的工件截面凸曲线是一段圆弧，这段圆弧的半径R 与AB 间的距离l 和OA 与OB 的夹角θ 有关，由(1)式求得。这种假设可以在步长变大时，使得圆弧更精确地逼近原轮廓线。

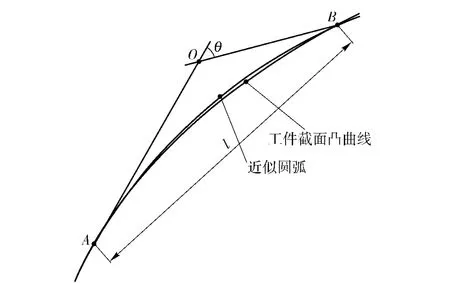
图6 直线包络方法刀触点计算示意图Fig.6 Schematic diagram of calculating cutter-contact points for grinding convex curve rotating member by lines enveloping method

通过简单计算可得

式中:h 是最大残留高度值;l 是两刀触点间的距离;θ 是外廓形线函数x =f(z)在相邻刀触点(z1x1)和(z2x2)处的法向量的夹角。

反过来，在图4坐标系中，对于任意的回转工件外廓形线函数x = f(z)，给出第一个刀触点A(z1x1)，最大残留高度h，求下一个刀触点B(z2x2).则(z2x2)满足公式(2)式恒成立。(2)式中:l 可由(3)式求得，θ 可由(4)式求得。

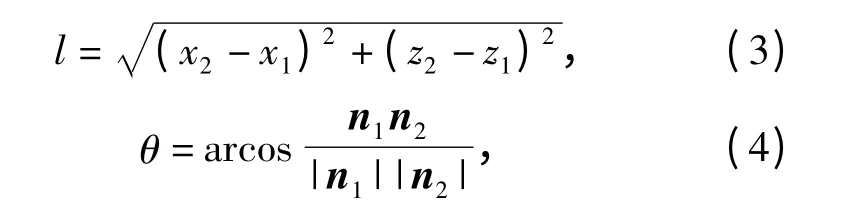
式中n1和n2分别是刀触点(z1x1)和(z2x2)处的法向量。

基于(2)式～(4)式重复计算，可以得出直线包络方法的基于等残留高度的所有刀触点坐标。直线需要转过的角度由上一刀触点处切线与Z 轴夹角和相邻的下一刀触点处的切线与Z 轴夹角之差求得。

同理，建立轨迹成形方法的基于等残留高度的刀触点求解模型。

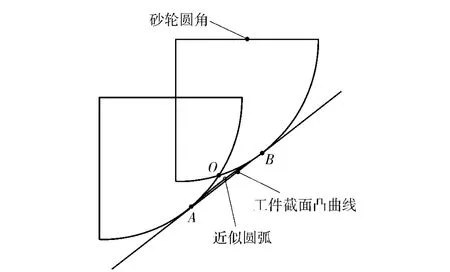
图7 轨迹方法的刀触点计算示意图Fig.7 Schematic diagram of calculating cutter-contact points for grinding convex curve rotating member by method of loci

如图7所示，砂轮圆角与工件截面轮廓相切于刀触点A、B，设刀尖圆弧半径为r.经计算，第二个刀触点(z2x2)满足(5)式恒成立。

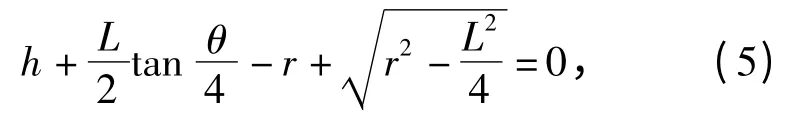
式中L 表示相邻两刀触点处砂轮圆角圆心间的距离，可由(6)式求得。θ 与(2)式中的意义和计算公式一样。

3 效率比较

从几何成型角度，比较轨迹法与直线包络法的效率就是在达到同样的最大残留高度情况下，比较它们各需要多少条环形加工带才能形成工件外廓，也就是比较计算出的凸曲线回转件截面轮廓曲线上刀触点的个数(一个刀触点对应一条环形加工带)，个数越多效率越低。

在图4坐标系下，给出一个普通的截面凸曲线方程z= -3-x2，所要达到的最大残留高度h=0.005 mm，第一个点的刀触点坐标为(-3，0)，计算到坐标点(-18，-3.87)停止。

分别采用直线包络法和轨迹法的刀触点计算公式，依次计算得到各个刀触点坐标、相邻两刀触点坐标的距离l(它反映了每次走刀环形加工区域的带宽，l 越大带宽越大，加工效率越高)和相邻两刀触点处法向量间的夹角θ(它反映了工件外廓形线的曲率半径大小，θ 值越小，此处的曲率半径越大)。

图8反映了这两种方法的加工效率和θ 的关系。可以看出，直线包络方法的加工效率随着θ 角的增大而减小，也就是加工效率随着工件截面凸曲线曲率半径的增大而增大，特别是在曲率半径很大(θ 值很小)的区域，加工效率比轨迹法提高了3～4 倍。

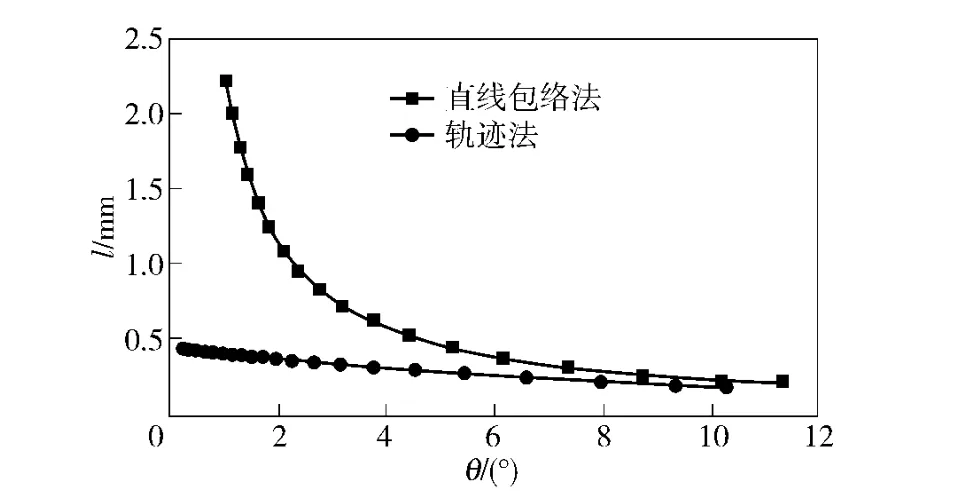
图8 加工效率和θ 关系图Fig 8 Diagram of connection between processing efficiency and θ

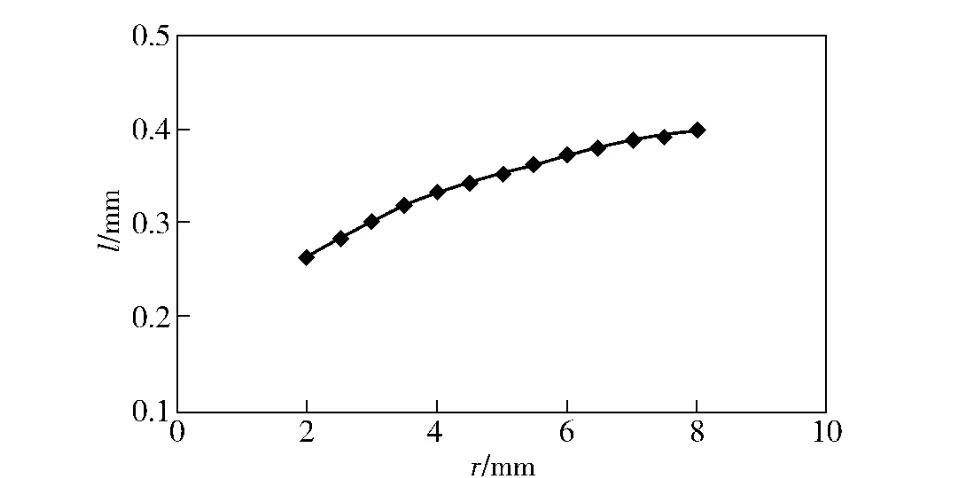
图9 轨迹法加工效率与砂轮圆角半径关系示意图Fig.9 Diagram of connection between processing efficiency of method of loci and radius of cutter chamfer

对于轨迹成形方法，在任一刀触点处，改变砂轮圆弧半径，计算得到和下一刀触点间的距离l.图9反映了轨迹成形方法加工效率和砂轮圆角半径的关系。由图8可以看出轨迹成形方法的加工效率和工件截面凸曲线的曲率半径变化关系不大。图9可以看出l 的值随着砂轮圆角半径变化情况。说明轨迹成型方法的加工效率随着砂轮圆角半径的增大而增大，但逐渐趋于平缓。因此，适当增大砂轮圆角半径可以提高轨迹法的磨削效率。

4 加工仿真

为了更直观反映直线包络法和轨迹法的加工效率，利用UG 软件的加工模块来进行仿真加工。采用垂直于驱动体模式模拟直线包络方法，这种加工模式就是不断改变旋转轴线的角度来使得刀具底面始终保持与工件截面凸曲线相切与刀具中心。实例为加工一个球体，为了清晰显示加工留下的残留区域和走刀轨迹，选用较大的残留高度h =0.5 mm.其中图10 是采用轨迹成形方法的加工结果，可以看出，球面需要17 条加工带才能完成。图11 是采用垂直于驱动体模式的加工结果，可以看出球面只需要5 条加工带即可完成，加工带数目减小了3～4 倍。与图1和图2比较可以看出，实际的加工轮廓与本文分析用的轮廓是一致的，直线包络方法的锥形加工带是一组相切直线包络出的，而轨迹成型方法是砂轮圆角轨迹磨削而成，加工带呈凹形。

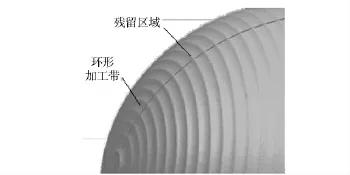
图10 轨迹法仿真图Fig.10 Simulation diagram of method of loci

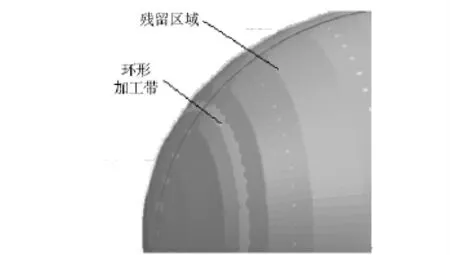
图11 直线包络法仿真图Fig.11 Simulation diagram of lines enveloping method

5 结论

本文介绍了加工凸曲线回转工件的直线包络法的成形原理，描述了利用平行砂轮与杯形砂轮来实现加工的方式。通过假设两任意点之间的工件截面凸曲线是一段半径与工件截面凸曲线方程，两点之间距离和两点处凸曲线法向夹角有关的圆弧，建立了直线包络方法和轨迹成形方法的基于等残留高度的刀触点计算模型。在达到相同最大残留高度的条件下，对直线包络方法和轨迹成形方法进行了效率比较，得出当工件截面凸曲线曲率半径较大时，直线包络方法的加工效率要比轨迹成形方法提高3～4 倍左右。

References)

［1］ 杜蕃.导弹整流罩外廓形线专用磨床开放式数控系统研究［D］.天津:天津大学，2005.DU Fan.Research of ONC system on special grinding machine for the exterior contour of radome［D］.Tianjin:Tianjin University，2005.

［2］ Zhang M M，Lin B.Du F.Creep feed surface grinding NC technology by cup wheel in radome machining［J］.Key Engineering Materials，2006，315:521 -525.

［3］ Choi Young-Keun，Banerjee A.Tool path generation for free form surfaces using Bezier curves/surfaces［J］.Science Direct，2007，(52):486 -501.

［4］ 苗春杰.UG 高级铣加工应用培训教程［M］.北京:清华大学出版社，2002.MIAO Chun-jie.UG advanced milling training course［M］.Beijing:Tsinghua University Press，2002.(in Chinese)

［5］ 董金华，刘顺芳.基于等残留高度的自由曲面三轴数控加工刀具轨迹规划［J］.煤矿机械，2008，29(7):92 -94.DONG Jin-hua，LIU Shun-fang.Tool-path planning for three-axis NC machining of free-form surfaces based on constant scallop height［J］.Coal Mine Machinery，2008，29(7):92 -94.(in Chinese)

［6］ 袁启海.导弹整流罩外廓形线缓进给磨削数控加工的实现［D］.天津:天津大学，2004.YUAN Qi-hai.The realization of NC creep grinding on the exterior contour of radome［D］.Tianjin:Tianjin University，2004.(in Chinese)