基于塔型对偶树方向滤波器组的弱小目标背景抑制方法
秦翰林,姚柯柯,周慧鑫,刘上乾,赖睿
(1.西安电子科技大学 技术物理学院,陕西 西安710071;2.西安电子科技大学 微电子学院,陕西 西安710071)
0 引言
在现代战争中,雷达面临着日益严重的对抗威胁,而无源或被动探测技术是解决雷达对抗威胁有效途径之一,其中利用被动红外探测是一个重要的研究方向,它能辅助雷达系统有效地提高区域防御系统的生存和反击能力。当目标距离很远时,其在红外像机光敏面上的成像面积非常小,且目标与背景的对比度较低,常表现为淹没在复杂背景(例如云层和地面条块边缘)中的几个像点,即为弱小目标。如果要可靠、稳定、准确地检测并跟踪这类目标,则必须对图像进行预处理,而高性能的背景抑制是其中重要而关键的一项预处理。
近些年来,红外弱小目标图像背景抑制技术得到较大的发展,主要有时域[1-2]、空域[3-7]、频域[8]、小波域[9]和偏微分方程理论[10]等方法。这些常见的红外目标背景抑制方法,满足了该领域的一些需求。然而,随着应用的发展,远距离的弱小运动目标的快速检测技术,成为新的迫切需求。但是,当背景为复杂的结构化背景时,这类滤波方法不能完全平滑边缘,从而导致检测概率降低,虚警率增大。在这种情况下,为了保留并有效地增强有用的目标特征信息,则必须对结构化背景实行自适应的抑制。
本文利用塔型对偶树方向滤波器组对红外图像细节信息的刻画能力,结合改进的视网膜皮层(Retinex)理论,提出一种新的塔型对偶树复方向滤波器组域红外图像背景抑制方法(PDTDFB-R).仿真实验结果表明,本文方法在实现对复杂背景杂波抑制的同时,可很好地保留并增强目标图像信息,是一种有效可行的红外图像弱小目标复杂背景抑制方法。
1 基于塔型对偶树方向滤波器组的目标背景抑制
1.1 塔型对偶树方向滤波器组
塔型对偶树方向滤波器组(PDTDFB)[11-12]是一种多尺度和多方向变换,且具有高角分辨率、低冗余度、可平移子带、提供局部相位信息和便于实现等特性。
PDTDFB 利用可平移塔型滤波器组和在每层的高通输出的对偶树2n 通道方向滤波器组(DFB)来实现,与对偶树复小波变换DTCWT[13]一样,对偶的DFB 具有对偶树的双通道结构,每个通道可解释为变换信号的实部和虚部,两通道的滤波器满足一定的条件,使得相互间满足二维希尔伯特条件,因而其对复小波基函数解析。PDTDFB 以拉普拉斯金字塔实现多分辨率分解,对高频子带,建立对偶树的变换结构获取平移不变性,每棵树均通过DFB 来实现,从而获得灵活的更高的方向性分辨率。图1分别给出了M 带方向滤波器组和3 层M 带PDTDFB 分解(M=8).
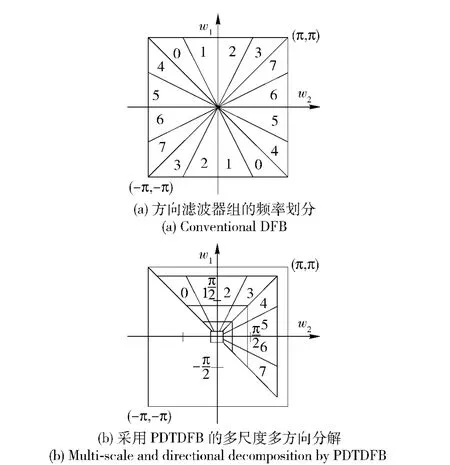
图1 频率划分Fig.1 Frequency partition
为构造一个可平移的多尺度多方向变换,PDTDFB利用多尺度滤波器组和DT-DFB 完成对图像的多方向和多尺度分析。图2给出了PDTDFB 的分解结构,图2(a)是分解部分,图2(b)是重构部分,块P 和Q 通过不断迭代来提供多尺度分解和重构,以获得多尺度表达。图1(b)为其对应的频谱剖分结果。
由此可见,PDTDFB 的基函数能提供丰富的方向和形状,有助于捕捉图像中的几何结构。小波变换是目前通用的图像处理手段,但对图像中曲线奇异的平滑性视而不见,影响了其实际的应用。而PDTDFB 具有多尺度、多方向、近邻界采样和各向异性等性质,改进和扩展了小波变换,在纹理检测和图像去噪[12]等方面有很好应用前景。
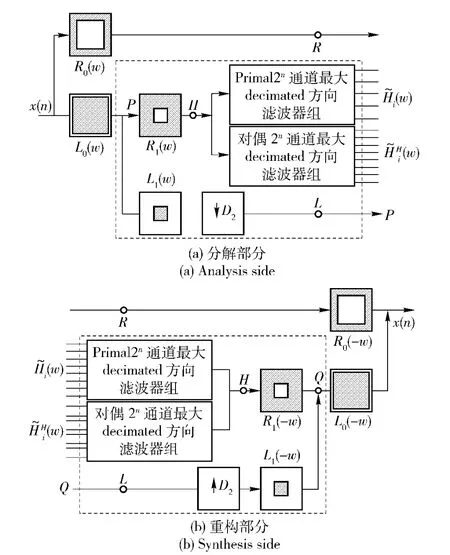
图2 塔型对偶树方向滤波器组结构[10]Fig.2 PDTDFB structure
红外弱小目标的红外辐射强度与周围复杂自然背景的辐射强度无关,目标的强度在整个图像序列中即使不是最强的,但与其所处的局部空间—时间域背景间的强度差异较明显,而且一般高于局部背景的辐射强度,具有各向异性特性;另一方面,强度较高的非目标背景图像通常与周围背景间无明显强度差异。由此可知,低频主要反映的是目标的背景杂波信息,高频主要是系统内部噪声和高亮区边缘,而目标信号主要在图像的中频区。因此,通过采用PDTDFB 对红外原始图像进行分解,得到不同尺度和方向的子带,由于背景与其它干扰的分解系数在各层间的相关量锐减,而含弱小目标的系数在层间的相关量衰减不快,同时,由于含弱小目标的分解系数能量范围逐渐扩大,在最粗糙一层(金字塔对偶树方向滤波器组分解的最后一层),弱小目标的分解系数完全影响了整个邻域的分布,可以认为此时弱小目标能量已经处于平稳状态,因此PDTDFB能有效捕获和表达二维空间域平滑曲面中的背景和弱小目标系数。
视网膜皮层理论在对数空间中,进行原图、原图和高斯函数卷积的值相减的操作,其实际上等于减去了图像中的平滑部分,而且高斯函数中R 越小,图像中慢变化的成分减去的也就越多,剩下的是图像中快变化部分,从而突出了原图中的细节信息。因此将其引入到金字塔对偶树方向滤波器组分解后子带系数的修改中,并将高斯函数设计为双曲线函数,通过此操作来修改系数达到保存并增强目标系数,抑制背景杂波系数的目的。
1.2 基于视网膜皮层理论的小目标背景抑制
视网膜皮层理论是由Land[14]于20 世纪70年代提出的一种颜色恒常知觉的计算理论。颜色恒常是指在照明发生变换的情况下,人们对物体表色的知觉趋向于稳定的心理倾向,同一表面在不同的照明下会产生不同的反射谱,人眼的颜色机制能分辨这种由照明变化导致的表面反射谱变化,然而人对该表面颜色的认知在一定的范围内却能保持恒定。Land 提出的中心/围绕空间对立视网膜皮层理论可以表示为(1)式的形式。
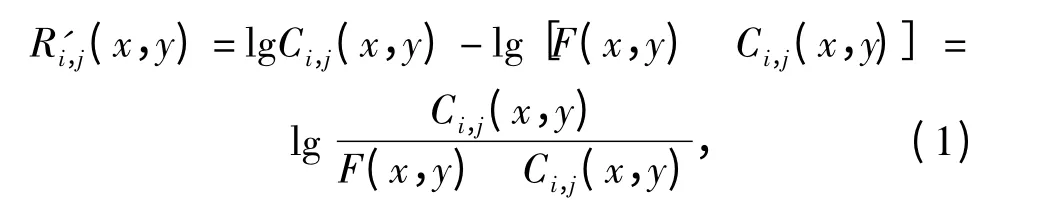
式中:R'i,j(x,y)为Retinex 的输出;Ci,j(x,y)为采用金字塔对偶树方向滤波器组的第i 尺度、第j 方向的子带图像;算子“ ”为卷积运算;F(x,y)为围绕函数,如(2)式所示。
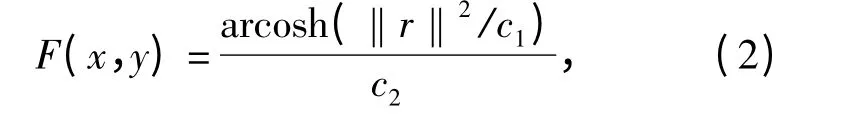
1.3 方法小结
本文利用PDTDFB 的多尺度、多方向性和平移不变性等优点,特别是平移不变性使得变换后子带的每个像素对应于原图的相同位置,可得到PDTDFB 分解后弱小目标位置的精确信息。方法具体步骤可以写成如下形式:
1)根据红外目标的大小及图像背景杂波的强弱,对输入图像用PDTDFB 变换N 层多尺度分解,将图像进行尺度和方向分离,分解后背景信息主要处于低频,目标信息和部分强杂波分别处于中频和高频区;
2)对获得的低频部分执行中值滤波,去除残留在低频部分的目标信号系数;
3)对高频子带图像分别采用设计的Retinex(1)式和(2)式进行处理,达到剔除目标信号系数的目的,并预测处于高频部分的背景;
4)采用PDTDFB 逆变换重构获得预测的背景图像;
5)将预测的背景图像与原图相减可得目标残差图像。
2 实验结果与分析
程序在Matlab7.1 软件平台环境下,主频为2.66 GHz,内存为2 GB 的PC 机上调试通过。在实验中,随机选取了几组有代表性的实测单目标红外图像序列进行实验验证。实验图像大小为128 像素×128 像素,信杂比为1 左右,对比度为7%左右。本文使用PDTDFB 分解层数N=3,塔型滤波器组采用“Nalias”,方向滤波器组采用“Pkva”,对3 组图像进行了仿真实验。图3(a)分别为3 个序列中的一帧原图,图3(b)和图3(c)为采用二维最小均方误差(TDLMS)[3]和最大中值(MMed)滤波方法[6]的处理结果,图3(d)为本文方法(PDTDFB-R)的处理效果。处理前后评价参数数值如表1所示,其参数定义由文献[10]给定。其中SCRin和CRin分别为原图的信杂比和对比度,ISCR 和ICR 分别为背景抑制后图像的信杂比和对比度增益,BSF 为背景抑制因子。
从实验结果可以看出,原图中目标仅占一个或几个像元,呈现为点状,无形状、纹理和结构特征,且强度较弱,特别是图3(a)中的目标更是被强烈的结构化云层和地面路网等背景杂波所干扰。TDLMS和MMed 方法处理后,目标虽然得到增强,大面积的背景也被抑制,但同时云层的边缘和地面建筑物的边缘也得到加强;这样必然会影响后续的检测跟踪处理。而采用本文方法处理后,在很好地保留并增强弱小目标信号的同时较好地抑制了复杂背景,图像信杂比和对比度增益分别达3 倍和4 倍以上,背景抑制因子达4 倍以上。
总体来讲,当目标受到大面积云层和地面杂波干扰时,与TDLMS 和MMed 滤波方法结果相比较,本文方法不但平滑了云层和地面道路内部,而且也能将云层和地面路网的边缘平滑掉,使得图像整体对比度和信杂比得到了很大改善。这是因为PDTDFB 变换保持有多尺度几何分析的多分辨性、局部性、多方向性和各向异性,而且具有良好平移不变性,能对图像中的围线信息有更好表示,保留原图特征信息的能力更强,也就具有了更好抑制边缘的能力。
3 结论

图3 不同方法性能比较Fig.3 Performance comparison with different methods
根据PDTDFB 变换对于具有轮廓奇异性的多变量函数有良好的逼近性能,提出了基于PDTDFB 的红外弱小目标背景抑制新方法,首先对红外原始图像采用PDTDFB 进行处理,使得图像中的背景边缘、纹理等特征得到了很好的逼近,并有效地保留了原图中的目标信息,然后采用设计的Retinex 理论函数抑制子带图像中背景边缘系数,即可将目标系数和背景杂波系数之间的差异拉大,最终便于实现对弱小目标信号的检测。和二维最小均方误差与最大中值两种方法相比,在不同背景杂波条件下,多组仿真实验结果均表明,本文方法可有效地抑制原始红外图像中较丰富的结构化背景杂波,而且在主观视觉和客观参数评价上都较好,并可有效地提取信杂比大于1.6 以上的目标信号。

表1 不同方法性能比较Tab.1 Performance comparison of different methods
References)
[1] Chen J Y,Reed IS.A detection algorithm for optical targets in clutter[J].IEEE Transactions on Aerospace and Electronic Systems,1987,23(1):46 -59.
[2] 吴一全,罗子娟.基于最小二乘支持向量机时域背景[J].兵工学报,2010,31(6):678 -684.WU Yi-quan,LUO Zi-juan.Small infrared target detection based on least squares support vector machine temporal background prediction[J].Acta Armamentarii,2010,31(6):678 -684.(in Chinese)
[3] Lin J N,Nie X,Unbehauen R.Two-dimensional LMS adaptive filter incorporating a local-mean estimator for image processing[J].IEEE Transactions on Circuits and Systems:Analog and Digital Signal Processing,1993:40(7):417 -428.
[4] 于劲松,万九卿,高秀林.红外图像弱小点目标检测技术研究[J].兵工学报,2008,29(12):1518 -1521.YU Jing-song,WAN Jiu-qing,GAO Xiu-lin.Research on dim point moving target detection in infrared image[J].Acta Armamentarii,2008,29(12):1518 -1521.(in Chinese)
[5] Hong Li,Yantao Wei,Luoqing Li.Infrared moving target detection and tracking based on tensor locality preserving projection[J].Infrared Physics & Technology,2010,53:77 -83.
[6] Deshpande S D,Er M H,Venkateswarlu R,et al.Max-mean and max-median filters for detection of small targets[C]∥SPIE Proceedings on Signal and Data Processing.Denver:SPIE,1999:3809:74 -83.
[7] Yilmaz A,Shafique K,Shah M.Target tracking in airborne forward looking infrared imagery[J].Imaging and Vision Computing,2003,21(7)623 -635.
[8] Porat B,Friedlander B.A frequency domain algorithm to multiframe detection and estimation of dim targets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(4):398 -401.
[9] Stephen DelMarco,Sos Agaian.The design of wavelets for image enhancement and target detection[J].SPIE,2009,7351:1 -5.
[10] Biyin Zhang,Tianxu Zhang,Zhiguo Cao,et al.Fast new small target detection algorithm based on a modified partial differential equation in infrared clutter[J].SPIE Optical Engineering,2007,46(10):106401-1 -6.
[11] Truong T Nguyen,Soontorn Oraintara.The shiftable complex directional pyramid—part Ⅰ:theoretical aspects[J].IEEE Transactions on Signal Processing,2008,56(10):4651 -4660.
[12] Truong T.Nguyen,Soontorn Oraintara.The shiftable complex directional pyramid—part Ⅱ:implementation and applications[J].IEEE Transactions on Signal Processing,2008,56(10):4661 -4672.
[13] Seesniek I W,Baraniuk R G.Kingsbu N C.The dual-tree complex wavelet transform[J].IEEE Transactions on Signal Processing,2005,22(6):123 -151.
[14] Land E H.Recent advances in Retinex theory[J].Vision Research,1986,26:7 -22.

