某型通用机枪大杠杆曲线参数优化研究

王瑞林，张本军，2，李永建，郝刚

(1.军械工程学院 火炮工程系，河北 石家庄050003;2.北京军事代表局 驻5413 厂代表室，河北 石家庄050030;3.总装通保部 军械器材供应站，北京100720)

某型通用机枪是目前我军步兵分队的主要自动武器，用以杀伤暴露的及轻型掩体后的集团有生目标和单个重要有生目标。然而，该枪存在首发装填困难的问题，一些体质偏弱的战士很难完成首发装填的工作，给部队的训练和使用带来很大的困扰，因此，需要对机枪的某些参数进行改进。

经试验研究发现，造成该枪首发装填困难的原因主要有:1)人机功效的问题，在装填过程中不便用力;2)装填阻力相对较大。对人机功效的优化需要对武器结构进行较大的改进，因此，本文从第2个方面进行优化研究。该机枪供弹机构中的大杠杆的曲线是影响首发装填的重要因素，可以通过优化该曲线的参数来达到减少首发装填阻力的目的。三次样条曲线是曲线拟合发展的活跃分支，它可以利用较少的点来拟合出较为复杂的曲线形状，且便于数床加工，已在凸轮设计、铁路曲线整正、飞机航迹生成以及自动机开闭锁曲线设计等方面得到了广泛的应用［1－5］;遗传算法是基于自然选择和基因遗传学原理的搜索方法，在对函数寻优求解时，对函数基本无限制，它即不要求函数连续，更不要求函数可微，且从理论上讲能够寻求到全局最优值，已被广泛的应用在参数优化中［6－10］。

本文利用三次样条曲线参数化大杠杆曲线，而后利用遗传算法对所建立的目标函数进行优化计算，以期得到一条使得目标函数达到最小的大杠杆曲线，从而为该枪的改进工作提供指导，也为同类型武器的设计和改进提供参考。

1 目标函数的确定

为分析首发装填故障产生的原因，利用线位移传感器做了首发装填过程的试验。试验装置示意图如图1所示。

图1 试验装置示意图Fig.1 Sketch of test apparatus

为了能够将传感器与通用机枪的运动部件联系起来，在试验过程中将机枪的枪管组件卸下，而后将传感器直接连接在机枪的活塞上，由于活塞的运动规律与装填拉柄完全一致，所以得到的信号处理结果即为装填拉柄的结果。针对不同的火线高做了3组试验共11 次，结果如图2～图4所示。

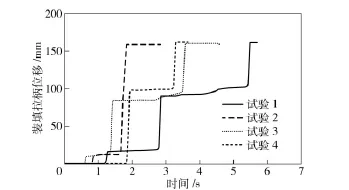
图2 第1 组试验曲线Fig.2 Test curves of group 1

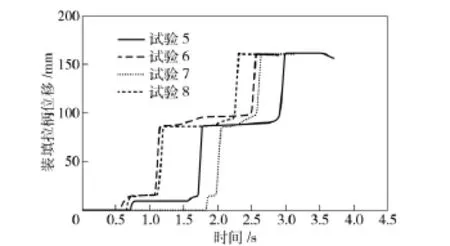
图3 第2 组试验曲线Fig.3 Test curves of group 2

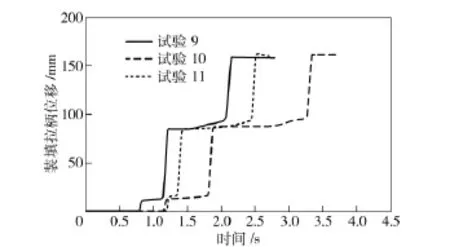
图4 第3 组试验曲线Fig.4 Test curves of group 3

从试验结果中可以看出，除第2 次试验外，均有2 次明显的停顿，而第2 次试验曲线则有1 次的停顿。通过对数值进行分析可知:这2 次停顿集中在14 mm 和86 mm 两点左右。通过分析受弹机各部件的运动可知:这2 点处为装填拉柄运动阻力的2 个极值点，而这2 个极值点是由拨弹滑板在向外划出和向里拨弹所受的阻力传递到拉柄运动方向上的最大值产生的。在首发装填过程中，阻力主要由两部分组成，即复进簧力和拨弹滑板传递的阻力。经试验发现，不装弹链时，拉装填拉柄并不困难，因此可以认为:拨弹滑板2 个阶段所受阻力传递到装填拉柄运动方向上的最大值是影响首发装填的重要因素。对于大杠杆曲线而言，拨弹滑板向外、向里2 个运动阶段对应是两段曲线。因此，本文分别以2 个阶段传递到拉柄上的最大力为目标函数，对2 个阶段的曲线进行优化计算。即

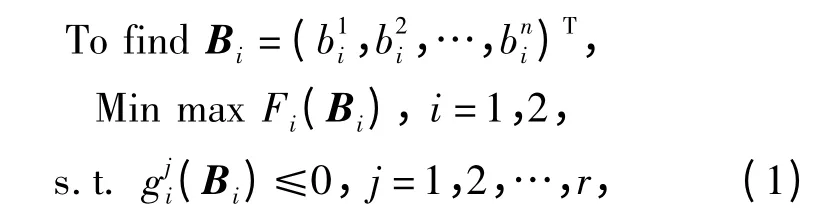
式中:i 为曲线段;r 和n 分别为约束条件和设计变量的个数;B 为设计变量组成的向量;F(B)为传递到拉柄上的力;g 为约束函数。

2 优化过程

2.1 待优化参数的确定

利用三次样条曲线进行曲线拟合时，5 个拟合点已经能够拟合出较为复杂的曲线形状，因此对每段曲线均选择5 个点进行拟合，如图5所示。

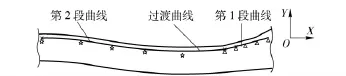
图5 设计变量示意图Fig.5 Sketch of design variable

图5中，△为第1 段曲线的拟合点，☆为第2段曲线的拟合点。由于第1 段曲线终点处的斜率和第2 段曲线起始点处的斜率差异很大，为使曲线的一阶导数连续，需在2 段曲线中间添加一条过渡曲线，如图5△和☆中间部分，该曲线可以由2 个圆弧组合得到。建立整体坐标系，X 轴和Y 轴的方向如图所示，坐标原点为大杠杆绕受弹机盖的旋转点。限定第1 条和第2 条曲线的起始点和终止点，其他各点X 轴坐标给定，Y 向坐标即为待优化变量，即

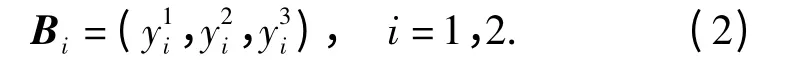
2.2 目标函数与待优化参数关系的求解

2.2.1 第1 段曲线几何关系

供弹机构的位置关系如图6所示，图中O 为坐标原点;O1为小杠杆的旋转点;A 为大杠杆上一点，在供弹机构工作过程中始终处于小杠杆上2 点C1和C2确定的直线上;D 为小杠杆始终与拨弹滑板接触的点;E 为枪机框带动的大杠杆滚轮上的点，在运动过程中始终与大杠杆曲线相接触。

图6 供弹机构示意图Fig.6 Sketch of feed mechanism

为简化计算，将第1 段曲线起始点的Y 向坐标定位0，这样只是平移了大杠杆的曲线，而对曲线的形状没有影响。利用三次样条曲线对参数点进行拟合，可得第1 段曲线方程y=f(x)，取其上一点H，坐标为(x0，y0)，则该点与E 点重合时大杠杆转过的角度β 为

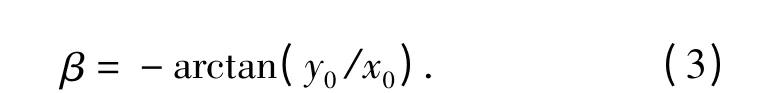
此时H 点的坐标为(x0cosβ－y0sinβ，0)，第1 段曲线变为y=φ(x).令O1点初始坐标为(a1，b1)，C1和C2点的初始坐标分别为(a2，b2)和(a3，b3)，A 点的初始坐标为(a4，b4)，当大杠杆转动β 后A 点的坐标(a5，b5)为

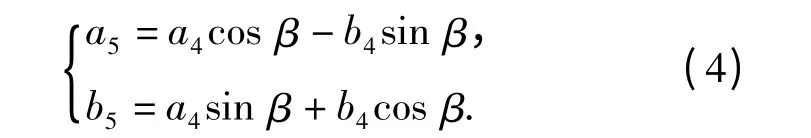
令大杠杆转动β 后小杠杆转动的角度为α，则此时C1和C2的坐标(a6，b6)和(a7，b7)分别为

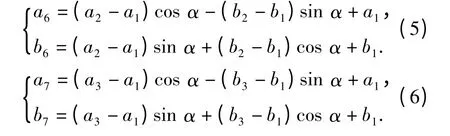
由于A 点始终处于直线C1C2上，所以可得

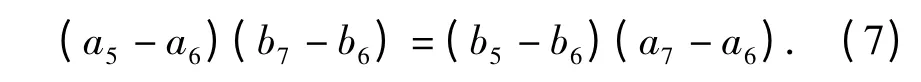
将(4)式～(6)式代入(7)式，化简后可以得到α 与β 之间的关系:

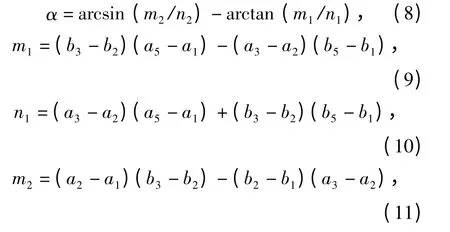
令D 点坐标为(a8，b8)，绕小杠杆旋转α 后的坐标(a9，b9)为

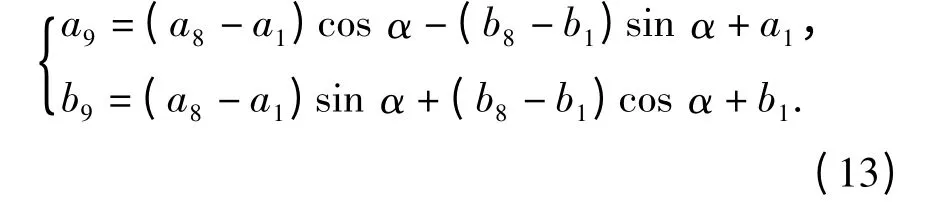
这样可以得到拨弹滑板的位移l 与待优化参数之间的关系式，即

2.2.2 第1 段曲线受力关系

该枪受弹机各零部件的质量比较小，且在首发装填的情况下其加速度也不大，因此可以不考虑各零部件的惯性力。在拨弹滑板向外滑动时，其所受到的力可以利用虚拟样机求得，记为P0(l).由供弹机构的传动关系可以得到，大小杠杆之间的作用力P1的方向与直线C1C2垂直，作用点为A 点。利用点到直线距离的公式可以得到P1相对于O1和P1相对于O 的力臂分别为

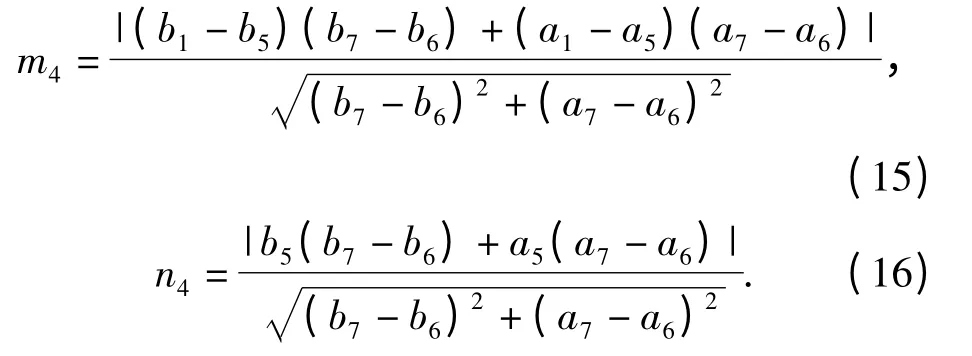
对小杠杆应用力矩平衡的条件可以得到

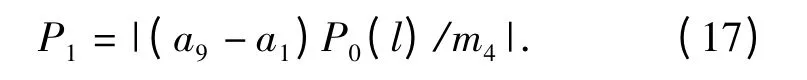
依据旋转后的曲线方程可以求得在H 点处曲线切线的斜率，记为k.则大杠杆与枪机框之间作用力F2的方向与切线垂直，作用点为H 点，则F2相对于O 的力臂为

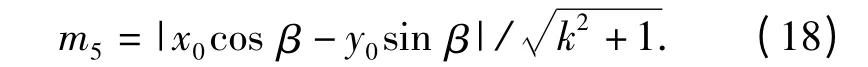
对大杠杆应用力矩平衡的条件可以得到

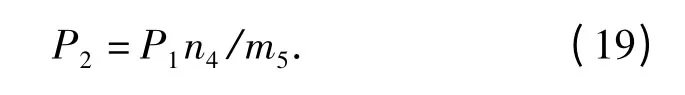
从而可以得到目标函数与待优化参数之间的关系式，即

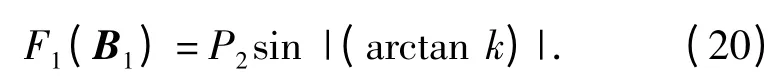
对于第2 段曲线，其起始状态为E 点运动到第1 段曲线的终止点处，记此时大杠杆转动的角度为β1，可以求出此时O1、A、C1、C2、D 以及第2 段曲线旋转后的方程y=φ(x)，利用第1 条曲线的推导思路，可以得到F2与B2之间的函数关系。

2.3 约束条件与待优化参数关系的求解

在第1 段曲线上任取两点(x1，y1)和(x2，y2)，其中x2＜x1＜0，即(x2，y2)为枪机框后到达的点。与这两点相对应的拨弹滑板的位移分别为l1和l2.依据供弹机构的要求，拨弹滑板要持续的向外滑动，则可得第1 段曲线的约束条件为

在第2 段曲线绕O 旋转β1后的曲线上任取两点(x1，y1)和(x2，y2)，其中x2＜x1＜0，依据供弹机构的要求，拨弹滑板要持续向里滑动

2.4 计算程序的编制

利用MATLAB 的M 文件对目标函数和约束条件进行编程，由于曲线的具体函数表达式比较复杂，所以在程序的编制过程中用数值进行了代替，其中第1 段曲线用100 个点代替，第2 段曲线用500 个点代替;目标函数中出现的导数则用微小增量的比值进行代替。

将编制好的M 文件代入MATLAB 的遗传算法工具箱，设定好初始种群、交叉概率和变异概率就可以对目标函数进行优化计算。

2.5 过渡曲线的求解

过渡曲线是由2 个圆弧组成，其共有6 个未知量需要确定。通过以上各步的求解可以得到第1 段曲线终止点处和第2 段曲线起始点处的斜率，这样就确定了4 个函数关系，再加上圆弧相切关系，在给定一个圆弧的半径后就可以求得过渡曲线的表达式。由于拨弹滑板位移的最大值出现在这段曲线上，因此在给定半径的时候要保证拨弹滑板位移的要求。

3 优化结果

将优化后的结果与优化前的结果相比较，如图7～图11 及表1所示。

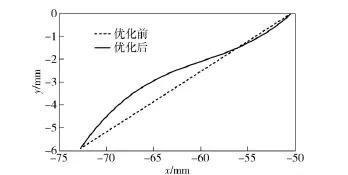
图7 优化前后第1 段曲线Fig.7 First curves before and after optimization

图8 第1 段曲线优化前后F1(B1)的值Fig.8 F1(B1)of first curves before and after optimization

从表1可以看出，通过优化使得第1 段曲线的目标函数减少了47.24%，第2 段曲线减少了39.3%，优化效果比较明显，达到了优化的目的。

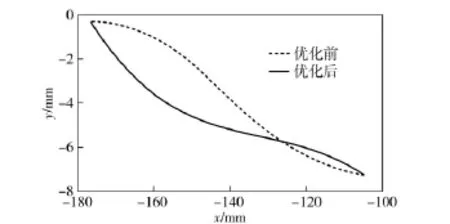
图9 优化前后第2 段曲线Fig.9 Second curves before and after optimization

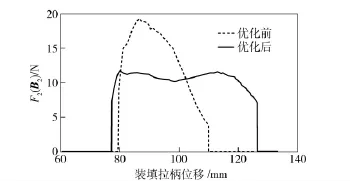
图10 第2 段曲线优化前后F2(B2)的值Fig.10 F2(B2)of second curves before and after optimization

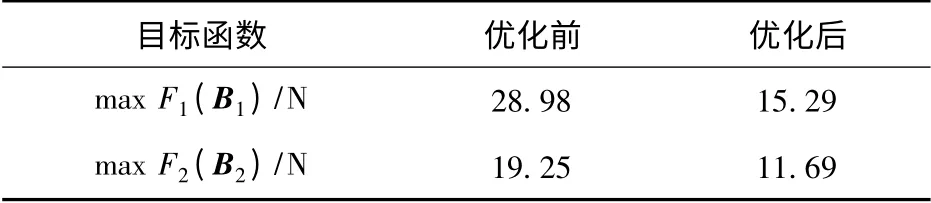
表1 优化前后目标函数Tab.1 Objective functions before and after optimization

4 结论

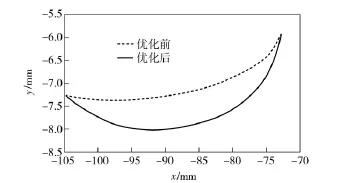
图11 优化前后过渡曲线Fig.11 Transition curves before and after optimization

某型通用机枪存在首发装填困难的问题，经试验研究发现，造成该问题的原因主要有:1)人机功效的问题，在装填过程中不便用力;2)装填阻力相对较大。本文就从第2 个方面进行了分析研究。利用线位移传感器进行了首发装填试验，得到了影响首发装填的重要因素，即拨弹滑板在向外和向里两个阶段所受阻力传递到装填拉柄运动方向上的最大值;在大杠杆的两段曲线上各取5 个点，利用三次样条曲线对这两条曲线进行拟合，求出了2 个最大值与插值点之间的函数关系;分别以这两个最大值为目标函数，以各插值点的Y 向坐标为待优化参数，利用遗传算法对大杠杆曲线进行了优化，使得两个目标函数分别减少了47.24%和39.3%，达到了优化的目的，为该枪的改进工作提供指导。同时，优化过程所使用的方法也为同类型武器的设计和改进提供参考。

References)

［1］ 侯悦民，张伟，鲍莉.利用三次均匀B 样条曲线优化设计凸轮廓线［J］.农业机械学报，2000，33(2):71－74.HOU Yu－min，ZHANG Wei，BAO Li.Optimization of cam contour by B－spline curve［J］.Transactions of the Chinese Society for Agricultural Machinery，2000，33(2):71－74.(in Chinese)

［2］ 秦方方，易思蓉，杨长根.基于三次样条曲线的铁路既有曲线整正方法［J］.中国铁道科学，2010，31(2):18－23.QIN Fang－fang，YI Si－rong，YANG Chang－gen.Method for the realignment of the existing railway curve based on the cubic spline curve［J］.China Railway Science，2010，31(2):18－23.(in Chinese)

［3］ 张新桥，钱志良，杨治.用非均匀B 样条曲线优化设计凸轮廓线［J］.机械设计，2004，21(1):40－42.ZHANG Xin－qiao，QIAN Zhi－liang，YANG Zhi.Optimal design of cam profile by means of non－uniform B－spline curve［J］.Journal of Machine Design，2004，21(1):40－42.(in Chinese)

［4］ 张瑞峰，倪世宏，于莹潇.基于Cardinals 三次样条曲线的航迹生成算法实现［J］.飞机设计，2005，(1):37－39.ZHANG Rui－feng，NI Shi－hong，YU Ying－xiao.Algorithm of generating flight paths using Cardinals spline［J］.Aircraft Design，2005，(1):37－39.(in Chinese)

［5］ 李鹏.大口径狙击步枪动力学仿真及结构参数优化研究［D］.石家庄:军械工程学院，2007.LI Peng.Research on dynamics simulation and structure optimization of large caliber sniper rifle［D］.Shijiazhuang:Ordnance Engineering College，2007.(in Chinese)

［6］ 张成强，陈捷，马旭.一种基于遗传算法的铣削参数优化的方法研究［J］.液压与机床，2010，38(7):39－41.ZHANG Cheng－qiang，CHEN Jie，MA Xu.Optimization methods of milling parameters based on genetic algorithm ［J］.Machine Tool ＆ Hydraulics，2010，38(7):39－41.(in Chinese)

［7］ Kim D，Rhee S.Optimal of arc welding process parameters using a genetic algorithm［J］.Welding Journal，2001，80(7):184－189.

［8］ Palanisamy P，Rajendran I，Shanmugasundaram S.Optimization of machining parameters using genetic algorithm and experimental validation for end－milling operations［J］.International Journal of Advanced Manufacturing Technology，2007，32(7－8):644－655.

［9］ 何景轩，田维平，何国强，等.基于遗传算法的固体火箭发动机参数优化设计［J］.固体火箭技术，2004，27(4):250－ 254.HE Jing－xuan，TIAN Wei－ping，HE Guo－qiang，et al The genetic algorithm for solid rocket motor parameter optimal design［J］.Journal of Solid Rocket Technology，2004，27(4):250－ 254.(in Chinese)

［10］ Quiza S R，Rivas S M，Alfonso B E.Genetic algorithm－based multi－objective optimization of cutting parameters in turning processes［J］.Engineering Applications of Artificial Intelligence，2006，19(2):127－ 133.

［11］ 张德丰.MATLAB 数值分析与应用［M］.北京:国防工业出版社，2009.ZHANG De－feng.Numerical analysis and application of MATLAB［M］.Beijing:National Defense Industry Press，2009.(in Chinese)

［12］ 龚纯，王正林.精通MATLAB 最优化计算［M］.北京:电子工业出版社，2009.GONG Chun，WANG Zheng－lin.Master the optimization calculation of MATLAB［J］.Beijing:Publishing House of Electronics Industry，2009.(in Chinese)