膛口初始流场对火药燃气流场影响的数值研究

郭则庆，王杨，姜孝海，李鸿志

(南京理工大学 瞬态物理国家重点实验室，江苏 南京210094)

枪炮发射时，膛口附近产生了包括初始射流、火药燃气射流以及弹丸相互作用的复杂流场。膛口流场的冲击波会对周边操作人员和设备产生损害，射流会对弹丸飞行产生扰动，影响射击精度。

前人已经针对膛口流场进行了大量的实验、理论和数值研究［1－9］。由于初始射流的压力通常比火药燃气射流低一个数量级以上［3］，因此针对初始流场影响的应用研究相对较少。

Schmidt［2］采用实验的方法测量了初始流场对膛口气流参数的影响。Klingenberg 等［3］采用实验方法研究了不同初速条件下的初始流场对火药燃气流场的影响。文献［5－6］采用数值方法对初始流场的影响进行了定性的分析。

为了进一步详细分析初始流场对火药燃气流场的影响并了解其影响机理，本文以7.62 mm 弹道枪作为研究对象，分别进行了实验和数值研究，模拟了有无初始流场条件下的近似真实形状弹丸的发射和膛口流场发展过程，比较两种条件下的流场特征，并进行了机理分析。

1 数值模型

1.1 控制方程

忽略粘性和化学反应，在体积可变的控制体内，理想气体的控制方程满足

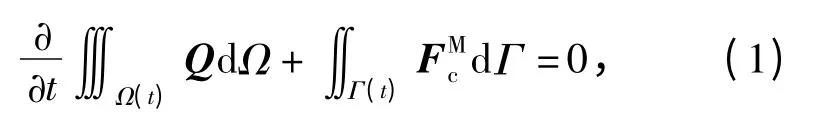
式中:Ω(t)为体积可变控制体;Г(t)为其外表面;Q，FMc分别为守恒量、无粘通量，

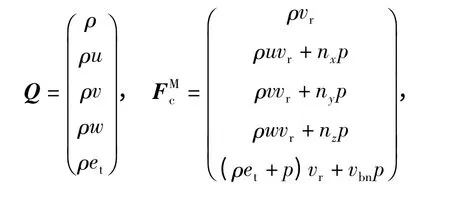
式中:ρ 为流体密度;u，v，w 分别为速度v 的分量;et为比总能;vbn为单元面dΓ 运动速度vb的法向分量，即vbn=vb·n;nx，ny，nz表示单元面dГ 的外法线单位向量n 的分量;vr为流体相对网格界面的法向运动速度，即

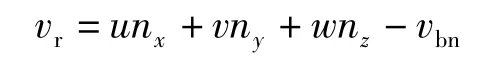
当界面速度vb= v 时，即vr=0，方程(1)为拉格朗日方程;当vb=0 时，为欧拉方程。故称方程(1)为ALE 方程。

引入理想气体状态方程以使方程组闭合

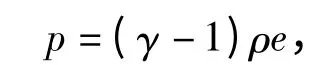
1.2 计算格式

控制体界面流量采用AUSM +格式求解，并且通过MUSCL 插值方法获得二阶精度，引入Minmod限制器以保证数值稳定性［10］。时间项采用Runge－Kutta 法求解。

1.3 计算域及边界条件

针对这种包含运动弹丸膛口流场的大位移运动边界的复杂计算，本文采用分区结构化重叠式贴体动网格，如图1所示。计算域采用两套网格［10］，分别为附着网格和背景网格。背景网格覆盖整个计算域，附着网格附着于运动弹丸周围，它由图1中1，2两个区域构成。

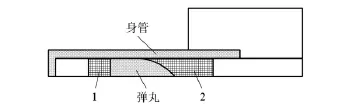
图1 计算域及部分网格示意图Fig.1 Sketch of computational area and grid

运动网格的左右边界位置固定，并与背景网格的某一列网格点重合，弹丸表面网格与弹丸速度相同，其他网格的边界速度按照线性分布给出。随着弹丸的运动，运动网格自动调节其疏密程度。当网格的尺度变化达到给定的临界值时，运动网格的边界向右移动一个网格，边界网格的参数通过双线性插值得到。

物面边界采用无粘滑移边界条件。对于无粘气体，静止的物面满足无渗透固壁条件，即物面法向速度满足(v－vb)·n=0.远场边界采用外推条件。

1.4 计算条件

分别模拟7.62 mm 弹道枪在有无初始流场2 种条件下的发射过程。对于含有初始流场条件，设置弹丸从膛底开始按内弹道给定的速度运动，并压缩弹丸前方空气。不含有初始流场条件下设置弹丸从膛口开始运动。

计算域如图1所示，身管内径d =7.62 mm，长96.2 d，考虑轴对称性，计算域为25 d×50 d，最小网格尺寸0.05 d.弹丸初速为798 m/s，弹底位置到达膛口时膛内气体压力与速度分布根据内弹道计算结果设置，膛外为常温常压大气环境。

2 结果与讨论

2.1 初始流场的影响

通过对比图2中实验照片［11］及有无初始流场条件下的数值计算结果来分析初始流场的影响。这里t=0 时刻为弹底位置与膛口重合瞬时。

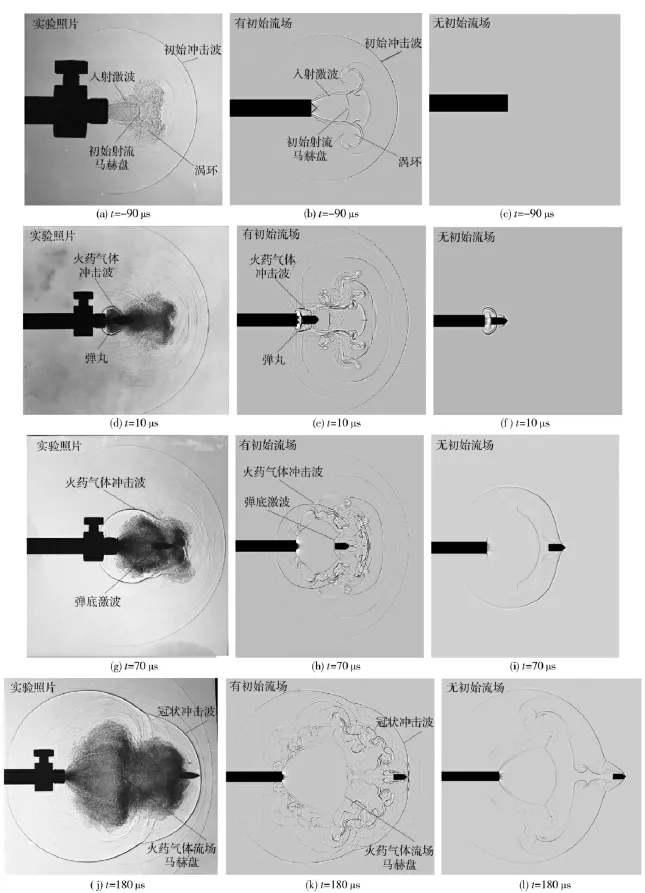
图2 实验阴影照片与数值模拟结果的对比Fig.2 Comparison between numerical and experimental shadowgraphs

比较图2中实验照片和有初始流场条件下的计算阴影照片可以看出，计算结果清晰的显示出了初始冲击波、入射激波、马赫盘、弹底激波、涡环、冠状冲击波等主要特征，并与实验照片对照的较好。

有初始流场条件下，弹丸出口前初始冲击波喷出膛口形成初始流场，初始冲击波波阵面近似呈球形(图2(b))，说明在各方向具有相似的膨胀特性。弹丸出膛口后(图2(e))，火药燃气从膛口喷出，并绕过弹丸，形成火药燃气冲击波。70 μs 时(图2(h))，火药燃气超越了弹丸，在弹丸前方形成一个复杂的火药燃气气团。高速射流受到弹丸的阻挡，形成面向上游的弹底激波。180 μs 时(图2(k))弹丸已经飞离超音速核心区，马赫盘已经形成，弹底激波也已消失，火药燃气团表现出显著的方向性，形成冠状冲击波和冠状气团。

在无初始流场的条件下(图2(c)、(f)、(i)、(l))，火药燃气冲击波始终没有超越弹丸，其波阵面近似为球形，没有冠状冲击波的出现。这与文献［7］得到的试验结果一致。弹丸做超音速运动，其压缩前方静止空气形成弹前弓形激波(图2(i)).需要注意的是弹前弓形激波和冠状冲击波在形成原因上有本质区别，前者是弹丸相对前方空气超音速运动引起的激波，而冠状冲击波的形成原因复杂。

另外，在初始流场的影响下，火药燃气流场参数发生了显著的变化。图3为有无初始流场2 种条件下火药燃气冲击波波阵面在轴线上的位置随时间变化的曲线。在不含初始流场条件下，冲击波的传播曲线近似为一条直线。而有初始流场条件下的火药燃气冲击波在0～20 μs 内(即火药燃气冲击波穿过初始流场马赫盘之前)的传播速度远大于不含初始流场的冲击波速度，在20～50 μs，火药燃气冲击波的传播速度有所下降，但仍然大于不含初始流场的情形。大约50 μs 后，火药燃气流场吞没了初始流场的高速气体区域，二者的冲击波传播速度基本一致。可见初始流场对穿过其所占区域的火药燃气起着定向加速作用。

膛口制退器等膛口装置的内部气体压力是其安全性设计中的一个重要参考因素。由于膛口装置内壁气体速度近似滞止，本文选取了近膛口区域内8 个位置点的滞止压力进行分析。表1为这些点在有无初始流场2 种条件下的最大滞止压力。可以看出，有初始流场时，流场中各点的滞止压力峰值均大于无初始流场条件。也就是说，初始流场的存在，增大了膛口冲击波压力峰值。因此，在进行膛口装置的设计时，应该考虑初始流场的影响。而传统的膛口装置设计方法均没有考虑初始流场的影响，而仅仅通过提高安全系数来保证其安全性。

从以上分析可以看出，初始流场对火药燃气流场的影响主要有:

1)初始流场对火药燃气流场结构上的影响主要是其导致了冠状冲击波的出现和马赫盘尺寸的变化。

2)在初始流场的影响下，近膛口流场区域的最大气体滞止压力最多可达无初始流场条件下的2.37 倍。

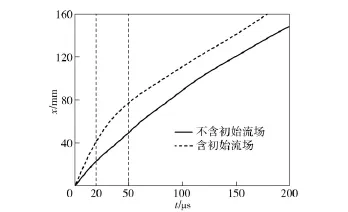
图3 火药燃气冲击波轴向传播距离对比Fig.3 Axial propagation distance of main shock

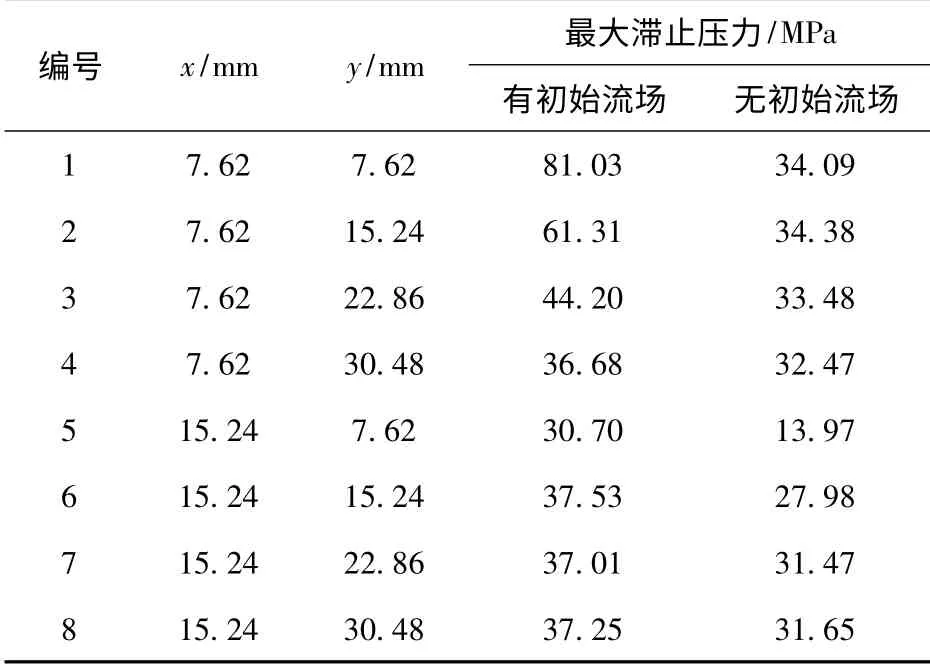
表1 有无初始流场的膛口最大滞止压力对比Tab.1 Comparison of maximum stagnation pressures

2.2 冠状冲击波形成机理

初始流场是冠状冲击波形成的原因，为了更加详细分析冠状冲击波的形成机理，首先描述初始流场的特征，然后通过增加t=4.5 μs 到t=72 μs 的计算阴影图来进行分析。

初始流场基本结构如图3(a)所示，由入射激波和马赫盘包围的区域为超音速核心区。该区域内为过膨胀气流，其具有以下几个特点:1)超音速，轴向速度Ma 为3.5 以上。2)低密度，最低约为外界空气密度的1%.3)该区域为一个细长的区域。

由于初始流场的存在，当弹丸离开膛口后，火药燃气从膛内喷射进入的不再是均匀静止的空气，而是有着复杂结构和流动特性的非均匀背景流场。而初始流场的超音速核心区的影响最为明显。

图4(a)为t=4.5 μs，膛内的高压火药燃气突然释放，在弹、膛环形区立即形成火药燃气冲击波。由于弹丸的阻挡，部分燃气首先向侧向运动。

图4(b)为t=18 μs，火药燃气高速喷出，弹底激波形成;受到初始流场超音速核心区域的影响，火药燃气射流在该区域内轴向运动速度较大，火药燃气冲击波轴向上出现一个向前突出的气团。通过比较可以看出，图4(b)中火药燃气冲击波突出部分径向尺寸与图4(a)图中初始流场的超音速核心区尺寸基本一致。

图4(c)为t=36 μs，来自上游的火药燃气不断补充并推动下游的压缩气团，其逐步演变为突出在前方的高压气团——冠状气团，而且其前突跃面呈现压力强间断面的特点。

图4(d)为t=72 μs，冠状气团形成后，在火药燃气的不断补充下，冲击波阵面追赶下游的初始流场的压缩波，最终合成一个强间断面——冠状冲击波。

从以上分析可以看出，冠状冲击波的产生是由于初始流场超音速核心区气体加速了火药燃气冲击波的轴向传播速度，形成向前突出的燃气气团，该气团不断被上游气体补充并追赶和叠加下游初始流场内的压缩波，最终形成冠状冲击波。

图4 有初始流场影响的火药燃气流场发展过程Fig.4 Progress of propellant flow

3 结论

1)初始流场对火药气体流场的发展有重要影响，包括冠状冲击波的形成、膛口区域滞止压力的增加等。

2)初始流场的存在提高了近膛口区域气体的滞止压力。因此，在进行膛口装置的设计时应该考虑初始流场的影响。

3)初始流场的影响主要在早期(火药燃气后效期时间的1/20)，对中后期的影响较小。在进行冲击波的中远场计算时，可以忽略初始流场。

本文的结论为膛口冲击波计算、膛口装置设计等提供了重要的参考价值。

References)

［1］ Gopalapillai R，Kim H D，Setoguchi T.On the near－field Aerodynamics of a projectile launched from a ballistic range［J］.Journal of mechanical Science and Technology，2007，21(7):1129－1138.

［2］ Schmit E M，Gordnier R E，Fansler K S.Interaction of gun exhaust flowfields［J］.AIAA Journal，1984，22(4):516－ 517.

［3］ Klingenberg G，Heimerl J M.Gun muzzle blast and flash［M］.Washington，D C:AIAA，1992.

［4］ 李鸿志，尤国钊.炮口冲击波的形成和分布规律以及对减少冲击波途径的分析［J］.华东工程学院学报，1977，(1):26－48.LI Hong－zhi，YOU Guo－zhao.The formulation，distribution and reduction of muzzle blast［J］.Journal of East China Engineering Institute，1977，(1):26－48.(in Chinese)

［5］ Ma Da－wei，Li Hong－zhi.The application of high－order godunov scheme to supersonic flow［C］∥First European Computational Fluid Dynamics Conference.New York:Elsevier，1992:1113－1119.

［6］ 马大为.含复杂波系膛口非定常流场的数值研究［D］.南京:南京理工大学，1991.MA Da－wei.Numerical study on the unsteady muzzle flow with complicated shock wave system［D］.Nanjing:Nanjing University of Science and Technology，1991.(in Chinese)

［7］ Merlen A，Dyment A.Similarity and asymptotic analysis for gunfiring aerodynamics［J］.Journal of Fluid Mechanics，1991，225:497－528.

［8］ 姜孝海，范宝春，李鸿志.基于ALE 方程的动网格膛口流场数值研究［J］.计算力学学报，2008，25(4):563～567.JIANG Xiao－hai，FAN Bao－chun，LI Hong－zhi.Numerical study on muzzle flow based on ALE equation and moving grids［J］.Journal of Computational Mechanics，2008，25(4):563－567.(in Chinese)

［9］ Jiang Xiao－hai，Fan Bao－chun，Li Hong－zhi.Numerical investingations on dynamic process of muzzle flow［J］.Applied Mathematics and Mechanics，2008，29(3):351－ 360.

［10］ 阎超.计算流体力学方法及应用［M］.北京:北京航空航天大学出版社，2006:124－127.YAN Chao.Computationalfluid dynamics method and application［M］.Beijing:Beihang University Press，2006:124－127.(in Chinese)

［11］ 李鸿志，姜孝海.弹道实验图集［R］.南京:瞬态物理国家重点实验室，2009.LI Hong－zhi，JIANG Xiao－hai.The album of experimental ballistics［R］.Nanjing:National Key Laboratory of Transient Physics，2009.(in Chinese)