车载电子机柜的缓冲设计

朱继元

(桂林电子科技大学信息科技学院，广西 桂林 541004)

高科技战争越来越依赖于电子技术，为了满足电子系统的高度集成化要求，电子设备的结构设计广泛采用了柜式结构。这种结构造价低廉，安装简便，并且和插入组件易于配合。在车载的环境下，由于地面的凸凹不平，使结构受到振动冲击作用，从而使电子机柜结构疲劳和强度下降。有文献报道了在一些雷达电子设备中，冲击引起的故障约占振动引起故障的1/4。

为了克服冲击对电子机柜的破坏，工程实际中常常是通过对电子机柜进行加固设计和采用缓冲设计，来保证电子机柜的正常工作。加固设计的成本通常较高，而采用缓冲设计，不但可以有效地抑制冲击的破坏作用，而且调整方便，工作可靠，成本经济，因而在生产实践中应用较为广泛。

1 电子机柜的理论模型

如图1所示，为电子机柜的结构图，电子机柜的总质量为m、隔振器的弹簧刚度为k、阻尼为c，如果仅考虑垂直方向的振动特性时，便可以将其简化为如图2所示的力学模型[1]，其力学模型为一个质量m、一个线性阻尼元件c和一个线性弹簧k组成的单自由度系统。

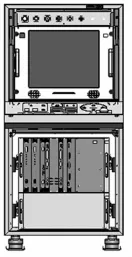
图1 电子机柜的结构图

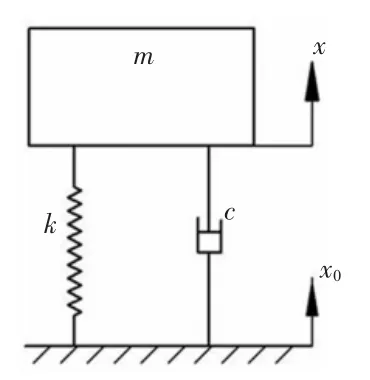
图2 电子机柜的力学模型

从而得电子机柜的位移[1]

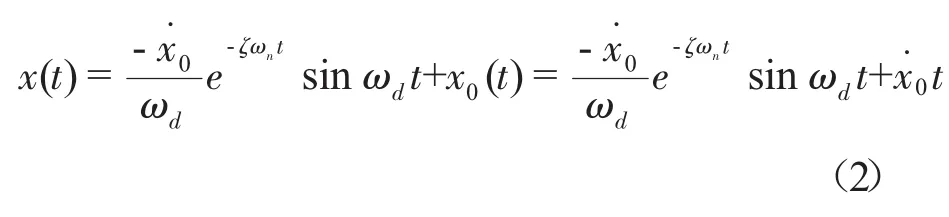
由式（2）可得电子机柜的位移

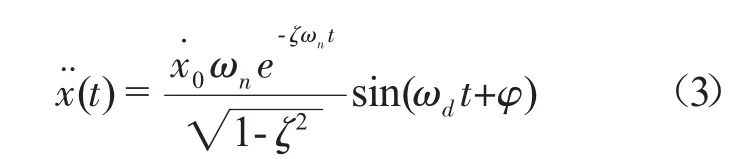
式中，

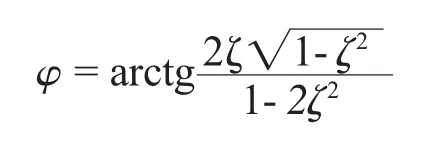
2 电子机柜的无阻尼缓冲设计

当电子机柜的阻尼为0时，阻尼比为ζ=0，此时式(1)和式(3)可化为

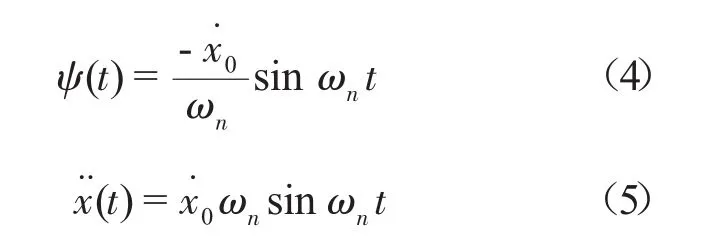
于是最大变形量和最在加速度可表示为

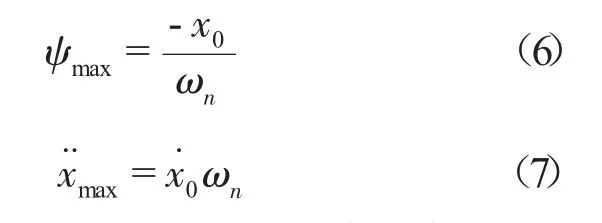
由式(7)可知，如果输入的阶跃速度不变，系统的固有频率越低，则电子机柜所受到的冲击加速度越小，此时缓冲效率也越高；但由式(6)可知，输入的阶跃速度不变，系统的固有频率越低，缓冲系统的最大变形量就越大。由此可知，缓冲效率高而变形量小的缓冲系统是不存在的，提高缓冲效率是以增大变形量为代价的，为了取得良好的缓冲效果，缓冲系统要能产生较大的变形，容许电子机柜产生较大的相对位移。

但由于工作性能及结构要求或受空间的限制，电子机柜不容许产生较大的相对位移，在这种情况下，如果满足变形条件，缓冲效率就受到了限制，如果此时缓冲效率满足不了设计要求，就不能用上述方法来进行缓冲设计，必须采用其他方法或将缓冲系统设计成非线性的[4]。

3 电子机柜的阻尼缓冲设计

可以求得出现最大加速度幅值的时刻tmax，

将式(10)代入式(8)和式(9)可得

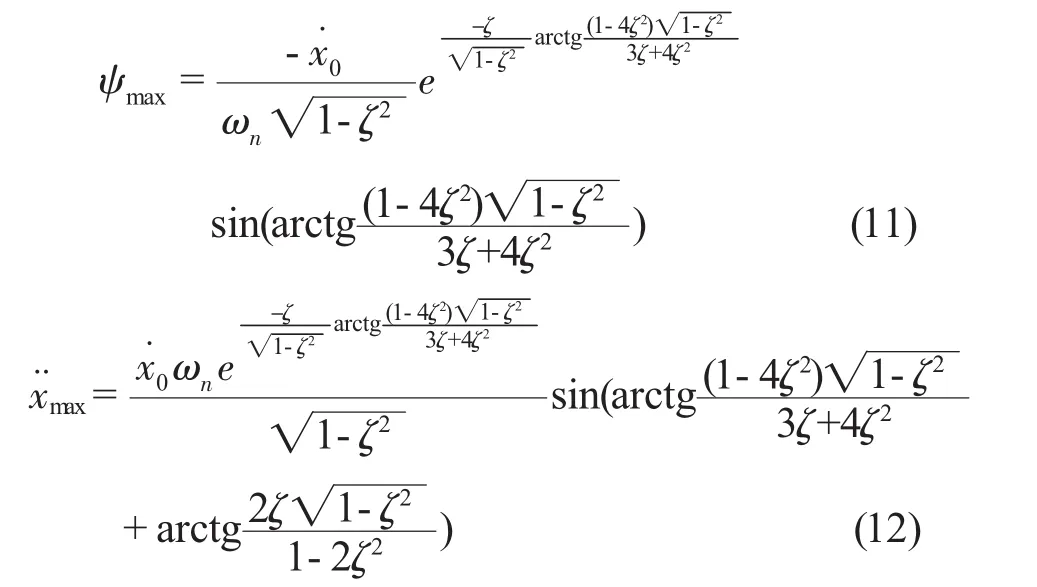
由式(11)和式(12)可知，当输入的阶跃速度不变时，当阻尼比为一确定值时，最大变形量是固有频率的函数，当取阻尼比为0.4时，这时，可以得到如图3和图4的曲线图。

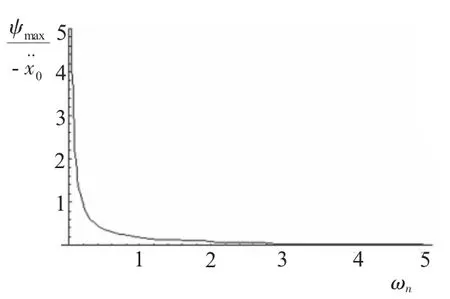
图3 最大变形量随固有频率变化曲线图

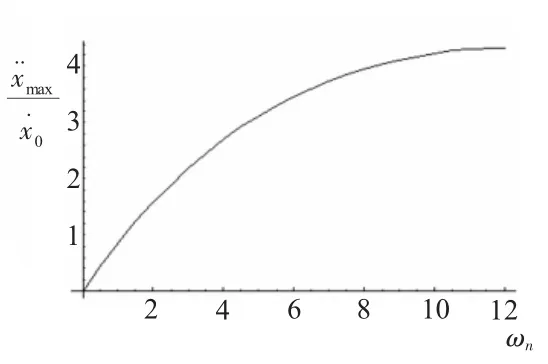
图4 最大加速度随固有频率变化曲线图

由图3和图4可知，当输入阶跃速度和阻尼比不变时，最大变形量随固有频率的增大而减小，而最大加速度随固有频率的增大而增大，这和无阻尼的情况一致。这意味着较小冲击传递率的情况下，缓冲系统的变形往往满足不了条件，满足了缓冲变形条件，又得不到最理想的传递率。所以在进行电子机柜缓冲设计时，在满足缓冲的变形条件下，设计机柜的刚度和强度。

为了讨论阻尼比对最大变形量的影响，在式(8)中把 ωnt看作自变量，把看作因变量，可以得到如图5所示的曲线图。讨论阻尼比对加速度的影响，在式（9）中把 ωnt看作自变量，把看作因变量，可以得到如图6所示的曲线图。

图5 阻尼比对变形量的影响

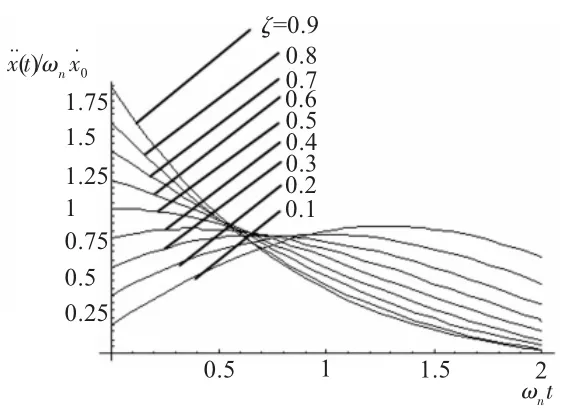
图6 阻尼比对加速度的影响

由图5可知，当输入阶跃速度和系统的固有频率不变时，阻尼比越小，缓冲系统的变形量越大，冲击持续的时间就会越长。所以在缓冲设计时，增大阻尼比，可以减小缓冲系统的变形量。而由图6可知，当输入阶跃速度和系统的固有频率不变时，阻尼比取的过大或过小，加速度的值都比较大。由此可见，存在最优阻尼比。对式(12)对阻尼比求导，并令其等于0，对其进行数值求解，得到当冲击的持续时间较短时，阻尼比取在0.265附近时，电子机柜的最大加速度最小。

4 结束语

无阻尼缓冲设计时，系统的固有频率越低，则电子机柜所受到的冲击加速度越小，此时缓冲效率也越高，而此时缓冲系统的最大变形量就越大；而在有阻尼缓冲设计时，系统固有频率的影响和无阻尼的情况相同，系统的固有频率越低，电子机柜的受到加速度越小，缓冲系统的变形越大。而阻尼比的增大，可以减小缓冲系统的变形量，阻尼比的过大或过小，都会使加速度值较大，当阻尼比取在0.265附近时，电子机柜的最大加速度最小。

[1]季 馨．电子设备振动分析与试验[Z]．南京：东南大学出版社，1992.

[2]鲁守来，季馨译．电子设备振动分析[Z]．南京：南京工学院241教研组，1983.

[3]丁文镜．减振理论[M]．北京：清华大学出版社，1988.

[4]马志宏，李金国．军用装备抗振动、抗冲击设计方法[J]．装备环境工程，2006，(10)：70-73.