穿孔管消声器横截面模态及消声特性的有限元分析

方 智，季振林

(哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001)

穿孔管消声器具有较低的流动阻力损失和良好的消声性能，在管道噪声控制中被广泛使用。为研究消声器中高频消声性能必须考虑高阶模态的影响。Munjal［1］利用分离变量法给出了矩形截面和圆形截面本征函数的解析表达式。Selamet等［2-3］根据模态节线的分布，应用模态匹配法研究了进出口位置和插管长度对圆管膨胀腔消声器消声性能的影响。Denia等［4-5］应用数值方法求解了椭圆截面的模态频率，应用模态叠加法分析了进出口位置和膨胀腔长度对椭圆形消声器声学特性的影响。Albelda等［6］利用元件模态综合方法研究了圆形截面穿孔管阻性消声器的横向模态，但给出的结果中并没有将穿孔管考虑进去。Selamet等［7-8］给出了圆形截面轴对称穿孔管的特性方程，但并未给出具体的模态结果。有关含有穿孔元件声学结构的横截面模态计算和分析的具体研究尚未见有文章发表。由于解析方法只适用于圆形或矩形同轴结构，对于截面为任意形状的结构，应使用数值方法。

本文研究的目的在于:① 基于伽辽金加权残数法，推导有穿孔元件存在时任意形状横截面本征值问题的有限元方程，利用状态空间原理将非线性特征值问题转换成标准的线性特征值问题，从而求出模态频率;② 对圆形同轴穿孔横截面，将有限元法计算结果与解析结果进行比较，检验有限元法预测穿孔管消声器横截面模态的有效性和精确性。③ 分析孔径、穿孔率和穿孔管偏移对穿孔管消声器的横截面模态频率和消声特性的影响。

1 横截面本征值问题求解的有限元法

图1为含有穿孔元件声学结构的横截面示意图。对于此类二维声学问题，区域S1和S2内的控制方程为:

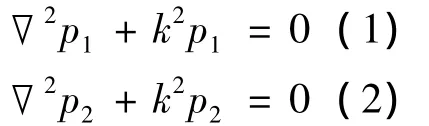
其中:p1和p2分别为区域S1和S2内的声压，k为波数。相应的边界条件为:

(1)刚性壁面边界条件，即法向质点振动速度为零，即:

图1 穿孔横截面Fig.1 Perforated cross-section

(2)穿孔壁面边界条件，假设穿孔两侧的法向质点振速连续，法向质点振速un和穿孔板两侧的声压差通过穿孔声阻抗ζp联系起来，即:

其中:ρ0为空气密度，c0为声速。穿孔声阻抗可表示为:

其中:φ为穿孔率，r=0.006为单孔的声阻，j为虚数单位，t'w=tw+αdh为穿孔管壁的声学厚度，tw为穿孔板壁厚，dh为穿孔直径，α为穿孔板的声学厚度修正系数，可表示为［9］:

由法向质点振速和压力梯度的关系可得:

利用伽辽金加权残数法和格林公式推导声学有限元方程［10］，从而可以得到含有穿孔元件声学结构横截面的特征方程。

区域S1内有:

其中，［K1］e=∫S1［▽N］［▽N］TdS为刚度矩阵，［M1］e=∫S1{N}·{N}TdS为质量矩阵，［］e= ∫Lp{N}·{N}TdL，［］e=∫Lp{N}{N}TdL为穿孔阻抗矩阵，下脚标e代表单元，{N}为形函数列向量。

将区域S1中的所有单元进行组装后可得:

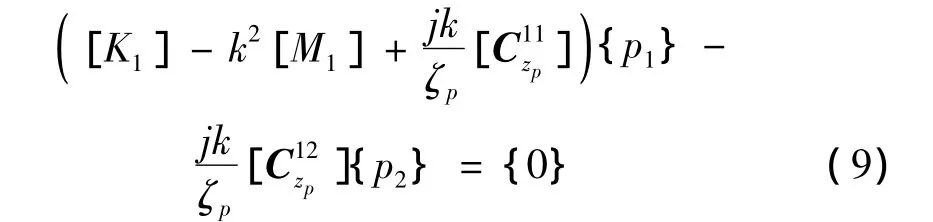
其中［K1］、［M1］、［］和［］分别由相应的各单元系数矩阵扩充而成。

同样，在区域S2内有:

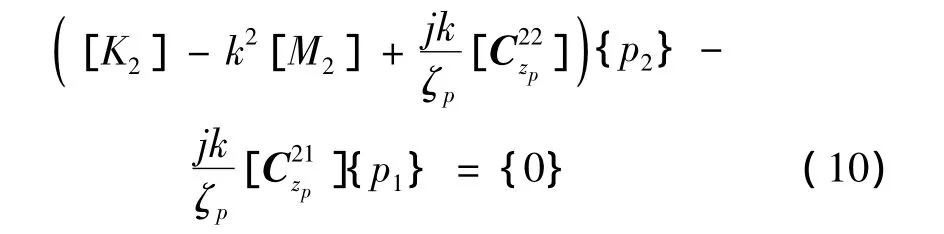
联合式(9)、式(10)得到:

式(11)即为含有穿孔元件声学结构的特征方程，求解该方程即可得到横截面的模态频率。由于该方程为非线性特征值方程，求解时，应用状态空间理论将非线性特征值方程转换为线性特征值方程。

将式(11)写成:

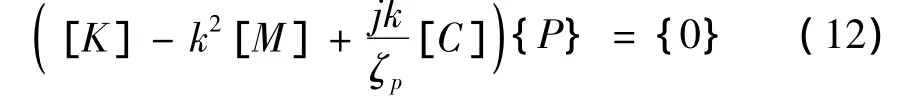
将式(5)代入式(12)，整理方程得到:

引入{PP}=k{P}，{PPP}=k2{P}，得到如下状态方程形式:

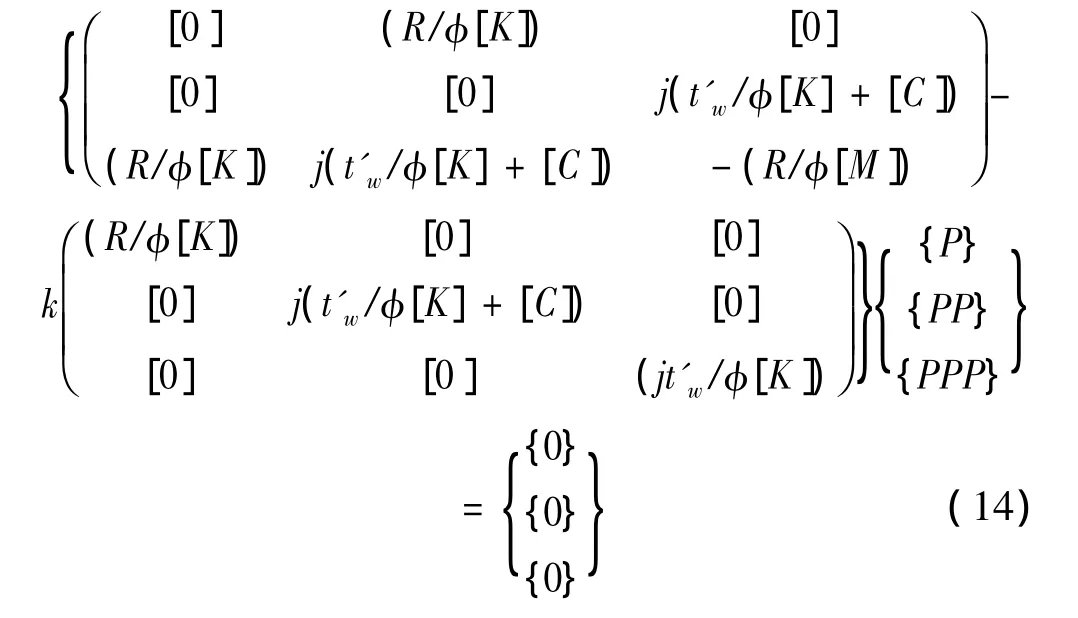
从而得到一个标准的特征值方程。通过求解此特征值方程可以求得所有特征值和特征向量。在穿孔阻抗边界条件下，其特征值为复数，从而构成所谓的复模态问题。在物理上，复特征值的实部对应模态的固有圆频率，虚部为模态衰减系数。

基于上述理论编写有限元计算程序，并将其应用于计算和分析穿孔管消声器横截面模态频率，进而分析消声器的消声特性。

2 算例及分析

为验证本文方法和编写的有限元计算程序的正确性，首先计算如图2所示的直通穿孔管消声器的径向模态频率，并与解析结果进行比较。由文献［7］可以得到特性方程:

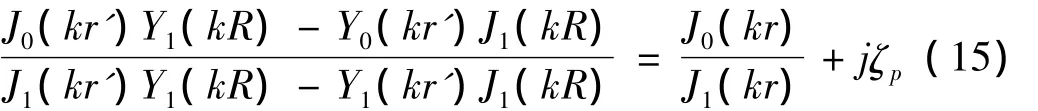
图2 直通穿孔管消声器Fig.2 Straight-through perforated tube silencer

对该方程求根即可得到径向模态频率的解析结果。

本文所用的消声器具体尺寸为:膨胀腔的内半径和长度分别为R=82.2 mm，L=257.2 mm，管道的内半径和外半径分别为r=24.5 mm和r'=25.4 mm，穿孔管壁厚为tw=0.9 mm，声速取344 m/s。

表1给出了使用有限元法和解析方法计算得到的穿孔率为φ=8.4%、孔径dh=4.98 mm的穿孔管消声器的径向模态频率。可以看出，两种方法计算结果吻合很好，相对误差在0.35%以内，从而验证了本文有限元法和编写的计算程序的正确性和计算精度。

表1 有限元结果与解析结果比较Tab.1 Comparison of FEM and analytical results

2.1 孔径对横截面模态频率的影响

表2给出了穿孔率为8.4%，孔径分别为2.49 mm和4.98 mm时消声器横截面的前4阶径向模态频率和模态形状。可以看出，孔径越大，相同阶次的高阶模态频率越低。图3比较了两种孔径的直通穿孔管消声器的传递损失。在传递损失曲线中，存在通过频率的拱形特性是声波以平面波形式传播的特征。拱形特性不再存在，说明高阶模态被激发，消声器内部出现高次波，声波以三维波的形式传播，消声器传递损失变差。从图3可以看出，孔径为2.49 mm的直通穿孔管消声器传递损失曲线在(0，1)阶模态频率(即2 188.6Hz)附近平面波特有的拱形特性消失，说明(0，1)阶模态被激发;而孔径为4.98 mm的直通穿孔管消声器传递损失曲线则在对应的(0，1)阶模态频率(即1 987.5 Hz)附近不再有平面波传播的特性。说明孔径越大，(0，1)阶模态频率越低，消声器内高次波出现的越早，中频消声效果变差。

?

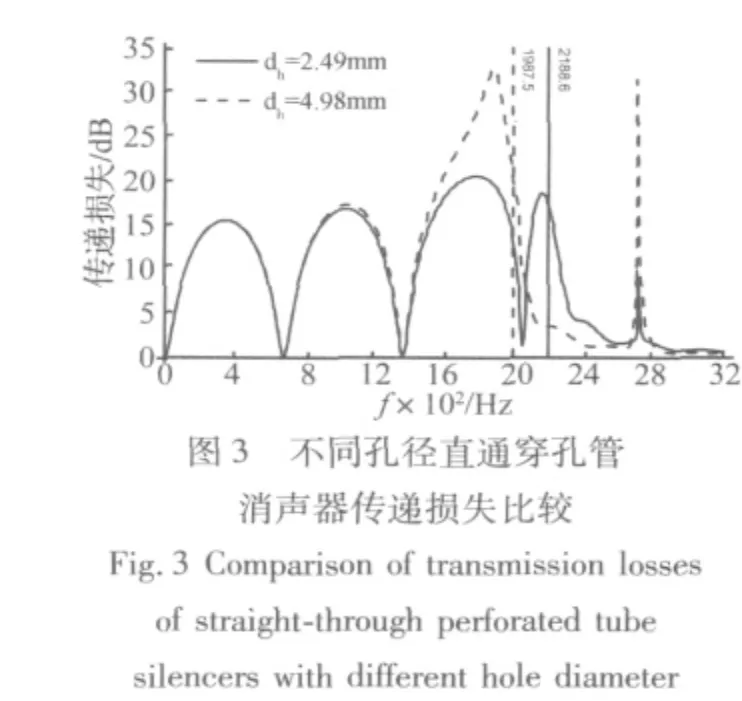
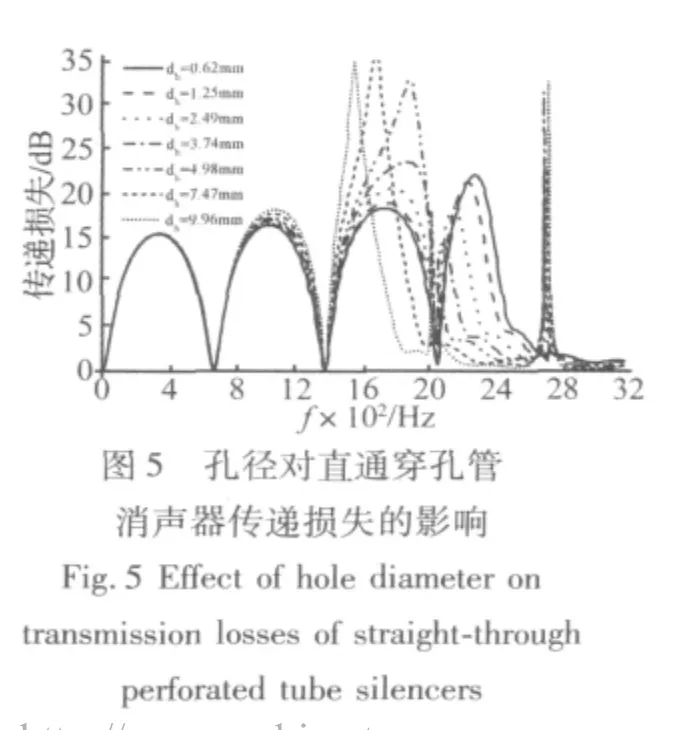
图4给出了穿孔率为8.4%时，孔径分别为0.62 mm，1.25 mm，2.49 mm，3.74 mm，4.98 mm，7.47 mm和9.96 mm几种情况下计算得到的横截面(0，1)阶模态频率。可以看出，在同一穿孔率下，孔径越大，(0，1)阶模态频率越低。图5则比较了不同孔径时直通穿孔管消声器的传递损失，可以看出，孔径越大，传递损失曲线上拱形不存在的频率越低，即平面波有效的频率范围越窄。

2.2 穿孔率对横截面模态频率的影响

?

表3给出了孔径为2.49 mm，穿孔率分别为2.1%和8.4%时前4阶径向模态频率与模态形状。可以看出，穿孔率越大，同一阶次的高阶模态频率越高。图6比较了孔径为2.49 mm，穿孔率分别为2.1%和8.4%时直通穿孔管消声器的传递损失。可以看出，穿孔率为2.1%的直通穿孔管消声器传递损失曲线在(0，1)阶模态频率(即1 367.9 Hz)附近不再有平面波特有的拱形特性，说明 (0，1)模态被激发;而穿孔率为8.4%的直通穿孔管消声器传递损失曲线则在对应的(0，1)阶模态频率(即2 188.6 Hz)附近不再有平面波传播的特性。说明穿孔率越大，消声器内高次波出现的越晚，平面波截止频率越高。

图9给出了几种典型穿孔率下不同孔径时横截面(0，1)阶模态频率分布。可以看出，穿孔率越低，孔径和穿孔率对(0，1)阶模态频率影响越大;孔径越大，(0，1)阶模态频率越低。随着穿孔率升高，(0，1)阶模态频率升高。穿孔率大于40%以后，孔径和穿孔率对(0，1)阶模态频率的影响较小。为增加有效的消声范围，孔径应减小，穿孔率应增大。为简便起见，当穿孔率高于40%以后，工程设计中可以忽略穿孔管的存在。

图6 不同穿孔率直通穿孔管消声器传递损失比较Fig.6 Comparison of transmission losses of straight-through perforated tube silencers with different porosity

图7 穿孔率对横截面(0，1)阶模态频率的影响Fig.7 Effect of porosity on cross-sectional(0，1)modal frequencies

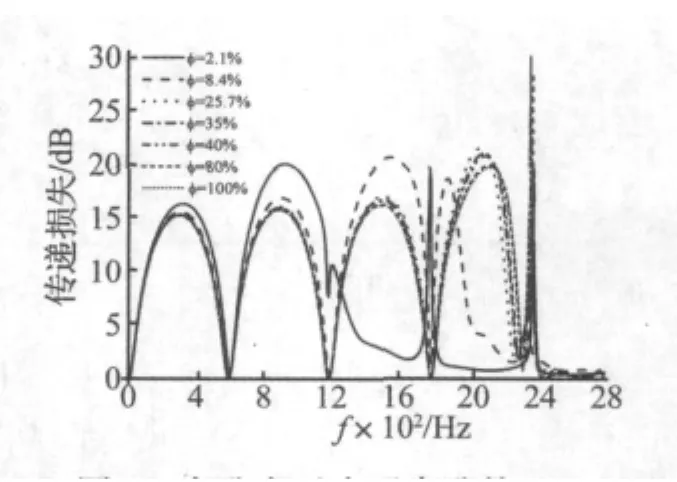
图8 穿孔率对直通穿孔管消声器传递损失的影响Fig.8 Effect of porosity on transmission losses of straight-through perforated tube silencers

图9 孔径和穿孔率对横截面(0，1)阶模态频率的影响Fig.9 Effect of hole diameter and porosity on cross-sectional(0，1)modal frequencies

2.3 穿孔管偏移对横截面模态频率的影响

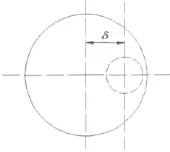
图10 穿孔管偏移横截面Fig.10 Cross-section with offset perforated tube

?

考虑图10所示的穿孔管偏移结构，表4比较了穿孔率为8.4%，孔径为2.49 mm，穿孔管分别偏移δ=10 mm，δ=30 mm和δ=55 mm时穿孔管消声器的前4阶横截面模态。由于穿孔管(进出口管)位于消声器第1阶模态的节线上，所以第1阶模态被抑制，第2阶模态首先被激发并传播。由表4可以看出，穿孔管偏移对消声器的第1和第2阶模态频率影响较小，但总体来讲，偏移量越大，第1和第2阶模态频率越高，但增加的幅度不大。图11比较了穿孔管偏移对消声器传递损失的影响，三种结构的消声器传递损失曲线拱形消失的频率接近，即平面波截止频率(第2阶模态频率)接近。

图11 穿孔管偏移时消声器传递损失比较Fig.11 Comparison of transmission losses of silencer with offset perforated tube

表5比较了穿孔率为8.4%，孔径分别为2.49 mm，4.98 mm和9.96 mm时穿孔管偏移消声器的第2阶模态频率。可以看出，孔径固定时，穿孔管偏移对消声器第2阶模态频率有一定的影响，但幅度较小。

表6比较了孔径为2.49 mm，穿孔率分别为2.1%，8.4%和16.8%时穿孔管偏移消声器的第2阶模态频率。可以看出，对于固定的穿孔率，穿孔管偏移对第2阶横截面模态频率的影响较小。

解析方法只能计算圆形同轴消声器的横截面模态。由于工程需要，不同轴穿孔管消声器应用也比较广泛，本文的有限元法不受几何形状的限制，可以计算任意截面形状消声器的横截面模态，为工程设计提供了一种有实用价值的计算方法。

表5 不同孔径时穿孔管偏移对消声器第2阶模态频率的影响Tab.5 Effect of perforated tube offset on the second modal frequencies of silencers with different hole diameter

表6 不同穿孔率时穿孔管偏移对消声器第2阶模态频率的影响Tab.6 Effect of perforated tube offset on the second modal frequencies of silencers with different porosity

3 结论

基于伽辽金加权残数法，推导了含有穿孔元件声学结构横截面的声学本征方程，利用状态空间原理将非线性特征值问题转换为标准的线性特征值问题。对于圆形同轴结构，横截面模态频率的有限元计算结果与解析结果吻合良好，从而验证了本文有限元方法及程序计算穿孔管消声器横截面模态的准确性。有限元数值计算结果表明，穿孔率低于40%，孔径越大，(0，1)阶模态频率越低，消声器中频消声效果越差;穿孔率越高，(0，1)阶模态频率越高，中频消声效果越好。穿孔率高于40%，孔径和穿孔率对(0，1)阶模态频率影响较小。对于固定孔径和穿孔率，穿孔管偏移对第2阶模态频率影响较小。

［1］Munjal M L.Acoustics of ducts and mufflers［M］.New York:Wiley-Interscience，1987.

［2］Selamet A，Ji Z L.Acoustic attenuation performance of circular expansion chambers with offset inlet/outlet:I.Analytical approach［J］.Journal of Sound and Vibration，1998，213(4):601-617.

［3］Selamet A，Ji Z L.Acoustic attenuation performance of circular expansion chambers with extended inlet/outlet［J］.Journal of Sound and Vibration，1999，223(2):197-212.

［4］ Denia F D，Albelda J，Fuenmayor F J，et al.Acoustic behaviour of elliptical chamber mufflers［J］.Journal of Sound and Vibration，2000，241(3):401-421.

［5］ Selamet A，Denia F D.Acoustic behavior of short elliptical chamber with end central inlet and end offset or side outlet［J］.Journal of Sound and Vibration，2001，245(5):953-959.

［6］ Albelda J，Denia F D，Torres M I，et al.A transversal substructuring mode matching method applied to the acoustic analysis of dissipative mufflers［J］.Journal of Sound and Vibration，2007，303(3-5):614-631.

［7］Selamet A，Xu M B，Lee I J.Analytical approach for sound attenuation in perforated dissipative silencers［J］.Journal of Acoustical Society of America，2004，115(5):2091-2099.

［8］Selamet A，Xu M B，Lee I J.Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extension ［J］.Journal of Acoustical Society of America，2005，117(4):2078-2089.

［9］康钟绪，季振林.穿孔板的声学厚度修正［J］.声学学报，2008，33(4):327-333.

［10］徐贝贝，季振林.穿孔管消声器声学特性的有限元分析［J］.振动与冲击，2009，28(9):112-115.