基于敏度分析的框架抗震优化

刘齐茂，燕柳斌

（1.广西工学院 土木建筑系，广西 柳州 545006；2.广西大学 土木建筑学院，南宁 530004）

结构的抗震优化设计属于结构动力响应优化设计的范畴，具有计算量巨大、优化设计问题建模非常复杂等特点，因此该领域的研究进展非常缓慢。根据各国规范的规定、震害经验和实验研究结果及工程实例分析，在地震作用下采用多高层建筑结构层间相对位移作为衡量结构变形能力从而判断结构是否满足建筑功能要求的指标是合理的。因此Zou等［1］建立以结构质量最小化为目标，同时满足层间相对位移和设计变量约束的优化数学模型，分别以振型分解反应谱法和时程分析法为基础推导出抗震优化设计准则，根据优化设计准则提出优化设计方法，是一种有效和实用的抗震优化设计方法，但该方法也存在不足，如只要求地震响应过程中层间相对位移在某些时点（加速度峰值及邻近的一些时点）满足约束条件，但实际上，当在优化过程中出现比较柔的结构时，层间相对位移响应的最大值并不一定出现在加速度峰值及邻近的一些时点，故该方法得到的优化设计在地震响应过程中不一定能满足约束条件，可能得到不可行的解。Lagarosa等［2］以时程分析法为基础，并考虑材料的非线性，采用进化算法求解了以结构质量最小化为目标，同时满足层间相对位移和设计变量约束的优化数学模型，但该方法由于采用随机搜索方法，存在计算工作量过大的缺点。黄冀卓等［3］以钢框架质量最轻和结构总动应变能最小为目标，基于相关的设计规范，给出了抗震钢框架多目标优化问题的一种合理提法，采用Pareto遗传算法求解抗震钢框架多目标优化问题，得到多目标优化问题的妥协解。结构抗震优化设计属于结构动力优化设计领域，结构动力优化设计方法从数学的角度看可分为零阶优化方法（非梯度类算法）［4］、一阶优化方法［5］和二阶优化方法。零阶优化方法不需要计算结构动力响应对设计变量的一阶导数，如粒子群方法［6］、遗传算法［7-8］和模拟退火算法［9］。一阶优化方法需要计算结构动力响应对设计变量的一阶导数如共轭梯度法［10］，一阶优化方法关键是计算结构动力响应对设计变量的一阶导数（也称敏度分析），国内外的学者已经发展了多种敏度分析方法［11-12］。二阶优化方法不仅需要计算结构动力响应对设计变量的一阶导数，而且需要计算结构动力响应对设计变量的二阶导数（也称Hessian矩阵分析），如牛顿类算法［13］，结构动力响应对设计变量的二阶导数的计算难度非常大，因此在国内外很少见到报道。通常，二阶优化方法的计算效率高于一阶优化方法，一阶优化方法的计算效率高于零阶设计方法。

本文的主要工作是Newmark-β法的基础上推导了层间相对位移对设计变量一阶导数和二阶导数的计算公式，建立结构抗震优化设计的数学模型，构造求解结构抗震优化设计问题二阶优化算法。最后演示了一个三层两跨的平面框架进行抗震优化设计，优化结果表明本文的抗震优化设计方法能获得结构的最优设计。

1 优化数学模型

框架具有i=1，2，3，…，N个单元组，单元的横截面为矩形，如图1所示，横截面的宽度（be）和高度（he）为设计变量。

为了讨论的方便，设计变量向量定义为：

框架抗震优化设计的目标函数为结构的质量，由设计变量表示为：

其中：ρ为材料的密度；li为第i个单元组中单元的长度；ni为第i个单元组所含单元的数目。

图1 平面梁单元Fig.1 Plane beam element

对高层建筑结构而言，结构的侧移通常成为设计的控制指标。高层建筑结构抗震设计必须限制结构的层间相对位移，因为过大的层间相对位移会使主体结构出现裂缝甚至破损，使结构产生附加内力，严重使会加速结构的倒塌，使填充墙及建筑装修出现裂缝或破损，使电梯轨道变形过大，使人不舒服，影响使用。《建筑抗震设计规范》［14］规定，以弹性方法计算的层间相对位移应满足以下条件：

式中，ΔuJ（t）为在t时刻第J层的弹性层间相对位移；uJ（t）和uJ-1（t）分别为在t时刻相邻的第J和J-1楼层的水平位移；HJ为第J层的高度；θJ为抗震设计规范规定的第J层层间转角；TT为地震的持续时间。

在抗震优化设计中，除了考虑层间相对位移的约束外，构件的强度和延性约束也是非常重要的，但由于问题本身很复杂，在本文中只考虑层间相对位移的约束（假设结构的侧移是结构设计的控制指标），但文中的优化设计方法将可推广到考虑构件的强度和延性约束、同时考虑受到静力和动力约束的情况，抗震优化设计问题通过式（1）～式（4）描述为：

本文将采用高效的牛顿类优化算法求解优化数学模型式（5），优化数学模型可通过积分型罚函数转变为一系列无约束优化设计问题，然后计算罚函数对设计变量的梯度和海森矩阵，从而可构造高效的牛顿类优化算法。由式（5）可见，要计算罚函数对设计变量的梯度和海森矩阵，必须计算层间相对位移和质量对设计变量的一阶和二阶导数。质量对设计变量的一阶和二阶导数的计算是很容易解决的问题，因此层间相对位移对设计变量的一阶和二阶导数的计算是解决问题的关键。

2 一、二阶导数计算

2.1 层间位移及其对设计变量的一、二阶导数

2.1.1 层间相对位移

初始条件：

其中：M、C、K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；x（t）、（t）、（t）分别为相对于地面的结点位移、速度和加速度；Eu为一向量，在节点线位移u方向、v方向和节点角位移θ方向上分别为1、0、0。

结构的阻尼矩阵采用瑞利阻尼如下：

其中，

式中，ω1、ω2分别为结构的第一、二阶固有频率；ζ1、ζ2为阻尼比，本文取 ζ1=ζ2=0.05。

将采用Newmark-β法求解（6）、式（7），框架在地震作用下层间相对位移响应的计算步骤如下：

（1）初始计算

其中，积分参数δ≥0.5，β=0.25（0.5+δ）2；⑤ 计算有效的刚度矩阵K*：

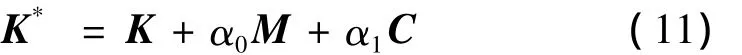
（2）计算t+Δt时刻的响应

① 计算t+Δt时刻有效的荷载向量F*：

② 计算t+Δt时刻的节点位移x（t+Δt）：

③ 计算t+Δt时刻的节点加速度（t+Δt）：

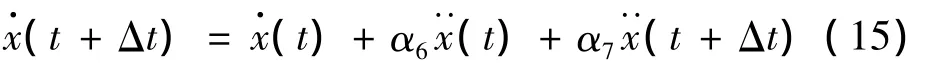
⑤ 用式（4）计算t+Δt时刻的层间相对位移ΔuJ（t+Δt）；

（3）重复（2）步骤①～⑤即可获得各个时刻的层间相对位移。

2.1.2层间位移对设计变量的一阶和二阶导数

式（13）两边分别对设计变量di求导一次，得：

其中，

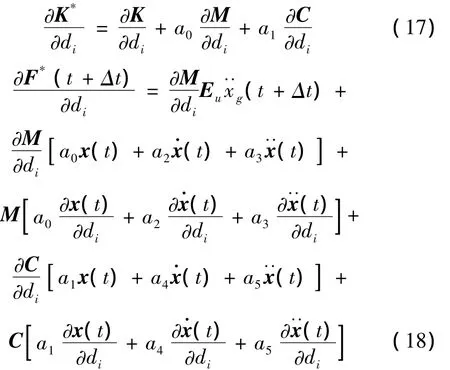
式（17）和式（18）分别通过式（11）和式（12）对设计变量di求导一次获得。

通过式（16）计算t+Δt时刻位移对设计变量di的一阶导数后，式（14）两边分别对设计变量di求导一次，得：

通过式（19）计算t+Δt时刻加速度对设计变量di的一阶导数后，式（15）两边分别对设计变量di求导一次，得：

式（4）两边分别对设计变量di求导一次，得到层间相对位移对设计变量的一阶导数：

式（16）两边分别对设计变量dj进一步求导，得：

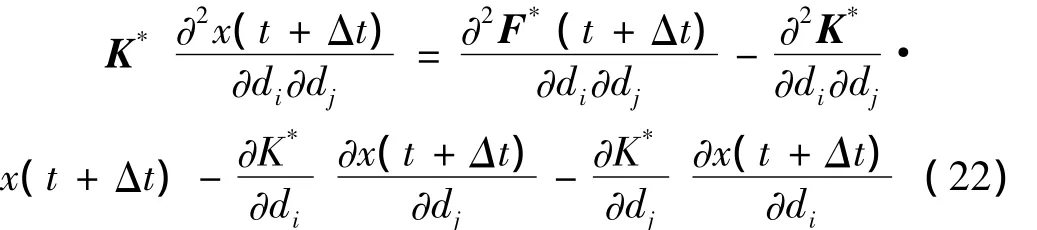
其中：

式（23）和式（24）分别由式（17）和式（18）对设计变量di求导一次获得。

由式（22）求得∂2x（t+ Δt）/（∂di∂dj）后，式（19）两边分别对设计变量dj求导，得：

式（21）两边分别对设计变量dj求导，得：

（1）初始计算

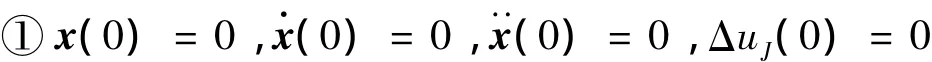
其中，积分参数δ≥0.5，β=0.25（0.5+δ）2；

⑥ 由式（11）计算K*。

（2）计算t+Δt时刻的响应

① 由式（13）计算t+Δt时刻的节点位移x（t+Δt）；

② 由式（14）计算t+Δt时刻 的节点加速度（t+Δt）；

③ 由式（15）计算（t+Δt）时刻的节点速度（t+Δt）；

④由式（4）计算t+Δt时刻的层间相对位移ΔuJ（t+Δt）；

⑤ 由式（16）计算t+Δt时刻的节点位移对设计变量的一阶导数∂x（t+Δt）/∂di；

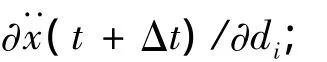
⑦ 由式（20）计算t+Δt时刻的节点速度对设计变量的一阶导数（t+Δt）/∂di；

⑧ 由式（21）计算t+Δt时刻的层间相对位移对设计变量的一阶导数∂ΔuJ（t+Δt）/∂di；

⑨ 由式（22）计算t+Δt时刻的节点位移对设计变量的二阶导数∂2x（t+ Δt）/（∂di∂dj）；

⑩ 由式（25）计算t+Δt时刻的节点加速度对设计变量的二阶导数∂2（t+Δt）/（∂di∂dj）；

(11) 由式（26）计算t+Δt时刻的节点速度对设计变量的二阶导数∂2（t+Δt）/（∂di∂dj）；

(12) 由式（27）计算t+Δt时刻的层间相对位移对设计变量的二阶导数∂2ΔuJ（t+Δt）/（∂di∂dj）。

（3）重复执行①～(12)步即可求得地震过程中各个时刻的响应。

2.2 结构质量对设计变量的一阶和二阶导数

式（2）两边分别对设计变量求导一次得结构质量对设计变量的一阶导数如下：

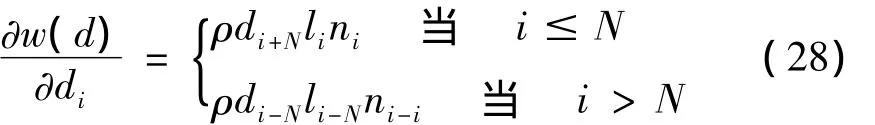
式（28）两边分别对设计变量进一步求导得结构质量对设计变量的二阶导数如下：

3 优化数学模型的求解

将数学模型（5）的约束条件规则化，得到等效的数学模型如下：

3.1 优化设计问题的转变

不等式优化数学模型（30）可通过罚函数转变为一系列无约束的积分形式的优化数学模型，为了求导的方便本文采用内点罚函数，如下：

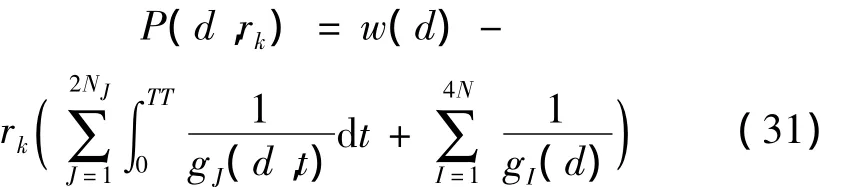
其中：罚系数rk是一递减数列，当rk→0，罚函数P（d，rk）的最小值逼近约束优化问题的最小值。因此，求解不等式约束优化问题（30）转变为求解一系列无约束优化问题如下：

罚系数的初始值r1由下式计算：

其中：d0为初始设计点，p0=1～50。在本文中p0=10。

罚系数rk根据下式递减：

其中：c=10～50，本文取c=10；k为搜索过程中使用罚函数的个数。

3.2 罚函数的梯度和海森矩阵

罚函数的梯度和海森矩阵即罚函数对设计变量的一阶和二阶导数，式（31）两边分别对设计变量di求导一次得罚函数对设计变量一阶导数如下：

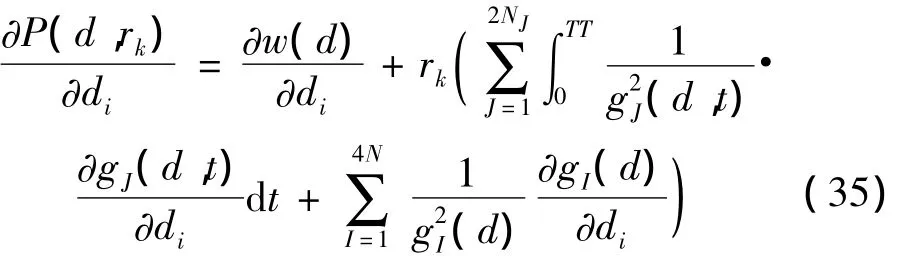
式（35）两边对设计变量dj进一步求导得罚函数对设计变量的二阶导数如下：

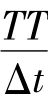
通过式（35）和式（36）计算罚函数对设计变量的一阶和二阶导数后即可获得罚函数的梯度和海森矩阵。

3.3 优化设计问题的求解

利用梯度和海森矩阵信息，构造求解不等式约束优化数学模型（30）的优化设计算法，其步骤如下：

第1步 选择可行的初始设计点d0，由式（33）计算罚系数的初始值，定义收敛容差ε1=10，令k=1；

第2步 从设计点dk-1出发，采用 Marquardt方法［15］求解优化数学模型（32）获得最优设计dk；用Marquardt方法求解优化数学模型（32）的步骤：

② 令i=0，λ（0）=105；

⑤i≥MI?是，执行第(11)步；否，执行第⑥步；

⑥计算

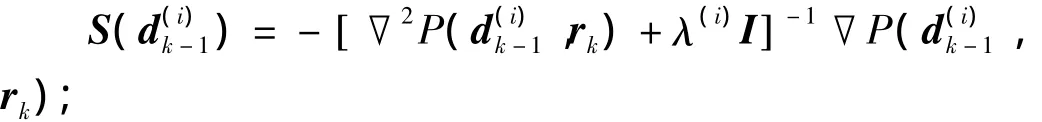
⑩ 令λ（i）=2λ（i），返回第⑥步；

第3 步P（dk-1，rk）-P（dk，rk）≤ε1?是，dk为最优设计，输出结果，停止计算；否，执行第④步；

第4步 由式（34）计算罚系数rk+1，k=k+1，回到第②步。

4 数值算例

一个三层两跨的平面框架如图2所示，假设每个楼层的质量为30 t，框架材料的弹性模量为20 GPa，阻尼比为5%，梁和柱的截面尺寸空间见图2的上方，层间转角限值为1/450，则第一层层间相对位移的限值为0.012 m，第二、三层的层间相对位移限值为0.008 m。

支座1，5，9受到El Centro水平地震加速度时程的激励，El Centro水平加速度峰值为0.349 g，记录时长为 8 s，步长 Δt=0.02 s。

从初始可行设计出发，通过4.3节的优化设计算法获得一系列优化设计如表1所示。

由表1和表2可见，随着罚系数逐步趋向于0，目标函数即结构的质量越来越小，优化设计逐步趋向于最优设计（r4=0.327和r5=0.032 7获得的优化设计），收敛时前后两次最优设计的质量不变，说明收敛精度非常高。初始可行设计的质量为156 735 kg，最优设计的质量为57 043 kg，结构的质量减轻了99 692 kg，最优设计的质量仅为初始可行设计的36.39%，优化效果明显。在优化过程中仅仅用了5个罚系数，说明优化算法的效率非常高。由表2还可看出，即使仅使用1个罚系数（r1=327），得到的优化设计也能得到极大的改善（质量由156 735 kg下降为82 876 kg，优化设计的质量为初始可行设计的52.88%）。

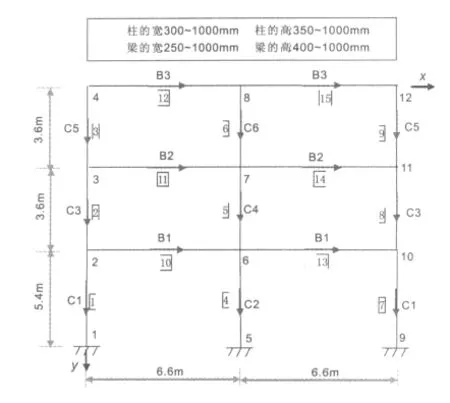
图2 三层两跨的平面框架Fig.2 A three-storey，two-bay planar frame

表1 初始可行设计和优化设计（单位：mm）Tab.1 Initial feasible design and optimal design（Units：mm）

表2 初始可行设计和优化设计的质量（单位：kg）Tab.2 Weight of the initial feasible design and optimal design（Units：kg）

初始可行设计和一系列优化设计的质量如表2所示。

5 结论

（1）提出一种计算层间相对位移对设计变量的一阶导数和二阶导数的方法，该方法只需要进行一次动力响应分析就可完成，具有非常高的计算效率。

（2）提出框架的抗震优化设计数学模型适用于结构的侧移是结构设计的控制指标的情况（如高层建筑）。当还要考虑其他设计指标时，需要在优化数学模型中增加响应的约束条件。

（3）采用积分型罚函数将显含时间参数的不等式约束优化问题转变为一系列不含时间参数的无约束优化问题，并且提出积分型罚函数梯度和海森矩阵的计算方法。但由于采用内点罚函数，因此初始设计必须为可行的设计。

（4）提出的优化算法充分利用梯度和海森矩阵的信息确定搜索的方向和步长，不需要进行一维搜索，下降速度快，具有良好的收敛性，能获得最优设计。算例表明该优化算法具有非常高的效率，并且在优化过程中能获得一系列可行的优化设计供工程设计人员选用。

（5）本文的抗震优化设计方法虽然只输入了一条地震波，但实际上可以同时输入多条地震波，只需要在优化数学模型中增加多个时程响应约束即可，计算方法基本不变。

［1］ Zou X K，Chan C M.An optimal resizing technique for seismic drift design of concrete buildings subjected to response spectrum and time history loadings［J］.Computers and Structures，2005，83：1689-1704.

［21］Lagarosa N D，Fragiadakisa M，Papadrakakisa M.Structural optimization：a tool for evaluating seismic design procedures［J］.Engineering Structures，2006，28：1623-1633.

［3］黄冀卓，王 湛.基于遗传算法的抗震钢框架多目标优化设计［J］.力学学报，2007，39（3）：389-397.

HUANG Ji-zhuo，WANG Zhan.Multiobjective optimization design of seismic steel frames using genetic algorithm［J］.Chinese Journal of Theoretical and Applied Mechanics，2007，39（3）：389-397.

［4］Kocer F Y，Arora J S.Optimal design of h-frame transmission poles for earthquake loading［J］.Journal of Structure Engineering，1999，125：1299-1308.

［5］ Arora J S，Cardoso J E B.A design sensitivity analysis principle and its implementation into ADINA［J］.Computer and Structure，1989，32：691-705.

［6］ Pereza R E，Behdinan K.Particle swarm approach for structural design optimization［J］. Computers and Structures，2007，85：1579-1588.

［7］ Togan V，Daloglu A T.Optimization of 3d trusses with adaptive approach in genetic algorithms［J］.Engineering Structures，2006，28：1019-1027.

［8］ Venanzi I，Materazzi A L.Multi-objective optimization of wind-excited structures［J］.Engineering Structures，2007，29（6）：983-990.

［9］ Lamberti L.An efficient simulated annealing algorithm for design optimization of truss structures［J］.Computers and Structures，2008，86：1936-1953.

［10］Fletcher R，Reeves C M.Function minimization by conjugate gradients［J］.Computer Journal，1964，6：163-168.

［11］Van Keulen F，Haftka R T，Kim N H.Review of options for structural design sensitivity analysis.part 1：linear systems［J］. ComputerMethodsin Applied Mechanicsand Engineering，2005，194：3213-3243.

［12］ Bogomolni M，Kirsch U，Sheinman I.Efficient design sensitivities of structures subjected to dynamic loading［J］.International Journal of Solids and Structures，2006，43：5485-5500.

［13］ Kirsch U，Bogomolni M，Van Keulen F.Efficient finitedifference design-sensitivities［J］.AIAA Journal，2005，43：399-405.

［14］ Broydon C G.Quasi-newton methods and their application to function minimization［J］.Mathematics of Computation，1967，21：368-381.

［15］ GB50011-2001，建筑抗震设计规范［S］.北京：中国建筑工业出版社，2001.

［16］ Reklaitis G V，Ravindran A，Ragsdell K M.Engineering optimization methods and applications［M］.New York：John Wiley＆ Sons，1983.