二级偏块振动磨主隔振机理研究与试验

杨小兰，刘极峰，邹景超，贾民平，高海涛

（1.南京工程学院 机械工程学院，南京 211167；2.黄河科技学院 工学院，郑州 450015；3.东南大学 机械工程学院，南京 211189）

在航空航天、冶金化工、机械电力、材料和医药等诸多领域的超细超微粉体制备方面，振动磨具有其他粉磨设备不可替代的技术优势，然目前国内外采用粉碎法制备超硬超细颗粒达到微米级水平，被业内称为极限［1-3］。

由于振动磨的运动状态极为复杂，它本身集介质、物料、磨筒等多相物质于一体，又常处于特殊机械力、特殊热应力以及特殊化学反应力等因素的联合作用下，不确定因素众多，加之振动磨整机质量大、负荷变化大，使得振动磨特别是大型、特大型振动磨的噪声大、功耗大等问题难以解决，且轴承、筒架等部件维修频次高，激振源故障频繁［4-5］，人们对振动磨方法的改造与创新自德国Gock教授后虽取得了一些推广和进步，但近年来尚未有根本性的工业化进展［6-7］。

针对现有技术的不足，欲解决振动制备超硬粉体超微化问题，实现系统具有一定频次的高振动强度（简称振强）是一种有效的途径，须同时面对三个难题：一是研制可产生具有一定频次的高振强、瞬态超高振强的激振器，二是研究系统对超高振强的有效控制，三是研究振动磨机结构及主隔振系统对高振强的适应；对问题一二作者已发表数篇文章及公开多项专利进行探讨［8-9］，研究问题三的基本思路是：将普通振动磨的单质体改造为双质体，形成主振与隔振两系统，主振系统采用非线性变节距硬特性线弹簧，形成具有储能节能功能的变刚度系统，使主振系统适应磨机变质量系统稳定工作的需求；隔振系统将考虑采用可产生大阻尼的隔振弹簧，有效吸收瞬态超高振强引起的振动，以获得较为理想的隔振效果。

1 磨机原理与结构分析

多级偏心块（简称偏块）振动磨是将普通振动磨使用的振动电机的一级偏块改为多级偏块（二级以上统称多级），也就是将多个偏块进行串接，串接级数k受结构限制，一般取k=2、3、4，分别称为二、三、四级偏块振动磨，串接后的机构自由度数即是偏块的级数，可见多级偏块机构均为输入1个自由度、输出多个自由度的不确定运动机构。

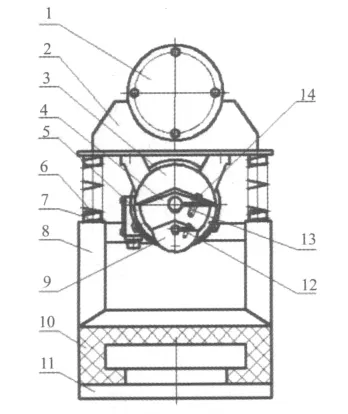
图1 振动磨机结构示意图Fig.1 Schematic diagram of vibration mill prototype

如图1所示磨机主要包括磨筒、上质体、振动电机、主偏块、副偏块、主振弹簧、导柱、下质体、二级偏块、隔振弹簧、底座、锁紧螺栓等零部件；磨筒安装在上质体之上；上质体与下质体之间通过主振弹簧及上质体和下质体上的弹簧导柱相联接；下质体通过减振弹簧支承在底座上；振动电机倒装在上质体的托板下，既是动力源又是激振源；工作时，上质体和下质体分别以不同的振幅和加速度振动。显然，上质体的振幅和加速度较大，可提高磨筒内介质对物料的冲击破碎能力；下质体的振幅和加速度较小，再通过隔振弹簧可大大减小传给基础的动载荷。

高振强的产生是基于如下情况：一方面磨机控制系统施以的变频控制技术，加之振动电机本身具有的速度、加速度波动，使得筒内介质、粉体与磨筒的多相物质将产生碰撞、冲击、剪切、挤压等复杂力学作用；另一方面多级偏块振动电机的运动不确定性，使得一、二级偏块在空间的质心相对位置变化复杂，呈现明显的多频多幅等特殊振动效果，能产生较宽的功率谱以及间断高振强、瞬态超高振强、瞬态大激振力等不规则性能，来完成振动磨一些特殊作业要求；此时的振动磨表现为多维、强耦合、运动参数多变等特点［10-11］，其运动方程具有明显的强非线性，可表为：

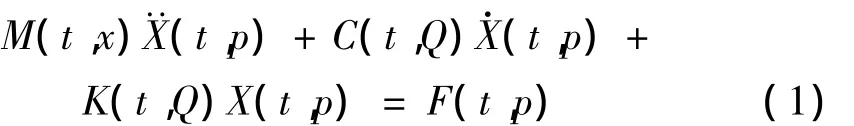
式中：M（t，x），C（t，Q），K（t，Q）为分别表示振动机系统质量、阻尼、刚度随时间、位置或载荷变化而变化的函数关系；（t，p），（t，p），X（t，p），F（t，p）为分别表示振动机系统加速度、速度、位移、激振力随时间、转角而变化的函数关系。

由式（1）可知，X为n维向量，振动磨机系统质量、阻尼、刚度随时间、位置或载荷变化而变化；位移、速度、加速度、激振力随时间、振频变化而变化，具有变质量、变阻尼、变刚度的强非线性特性，故此磨机称为强非线性振动磨［12-13］。

2 主振系统机理及分析

磨机主振系统由筒体、上质体、激振器及主振弹簧所构成，隔振系统由下质体、隔振弹簧所组成。筒体内装有超细颗粒物料及介质球，主振弹簧采用金属螺旋弹簧，支撑上下质体，下质体下端装有环形橡胶弹簧，以减少对地面的振动传递。

传统的振动磨机使用的弹簧一般为等节距线形圆柱螺旋弹簧，使用不等节距螺旋弹簧的节距变化可选择由小到大递增单向排列，也可选择按两端小中间大双向递增排列，从振动稳定性、设计对称性方面考虑，本设计采用后者［14-15］。

研究振动粉碎状态下超细超微颗粒粉碎机理，探讨降低颗粒的断裂阻抗、提高磨机多相物质碰撞冲击概率、增强碰撞冲击力和有助于颗粒断裂细化的条件，通过理论分析、数值模拟及试验可知［16-17］，主振弹簧采用非线性硬特性线，不仅能实现系统的节能降耗，且有利于提高系统的瞬态振动强度和激振力，可形成瞬态高振强振动粉碎状态下的粉体强碰撞行为，对于解决超微粉体的团聚、反粉碎、不细化等问题具有明显成效。

2.1 工作条件与分析

根据现场情况估算，空载时上质体包括激振器、筒体等质量m为120 kg，物料质量m1为20 kg，满载时上质体质量为140 kg。

现场有等节距弹簧6个，每个弹簧的原长为130 mm，在上质体的重力作用下变为116 mm，可得系统空载静止时弹簧在最小载荷作用下的变形量为14 mm。设弹簧的预期振幅为6～16 mm，则弹簧在最大动载荷作用下的最大变形量为25 mm。

设主振弹簧的非线性特性线方程为：

式中：F，f为系统在任一瞬时载荷及相应变形。

2.2 非线性硬特性线方程

根据系统受载情况，设主振弹簧的个数为6，由前述确定的质体质量，可得系统空载时单个弹簧所受载荷为：

系统满载时，单个弹簧所受载荷为：

考虑到：

（1）最小载荷情况即为未加物料时的静载荷情况，此时单个弹簧受力为F0。

（2）各弹簧受载荷不均匀引起的附加载荷，取各弹簧受载不均匀系数为1.4，则弹簧受到的最大静载荷为Fmax=1.4Fm=320.18 N

（3）依据经验，取5倍的最大静载荷作为最大动载荷［6，14］，则Fmax=5Fm=1 600.9 N

据此可得非线性特性线的三点坐标为C1（14，196）、C2（17，320.18）、C3（30，1 600.9）将其代入（2）式，得非线性弹簧载荷变形方程：

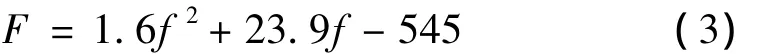
2.3 非线性主振弹簧设计分析

根据振动磨机工程现场情况及设计经验，取切变模量G=78.8 GPa，可得许用切应力［τ］=0.375σb=606.75 MPa，选取弹簧中径D为45 mm，簧丝直径d为8 mm，由旋绕比C=D/d=45/8=5.6，取曲度系数K为1.25［14］，则：

弹簧各圈刚度P'、各圈并圈后弹簧刚度F'i、各圈并圈时的载荷Fi、节距ti等计算结果见表1。采用MATLAB编程，通过改变弹簧中径D和簧丝直径d，可获得不同的弹簧质量及位移，进而检验结果的合理性。

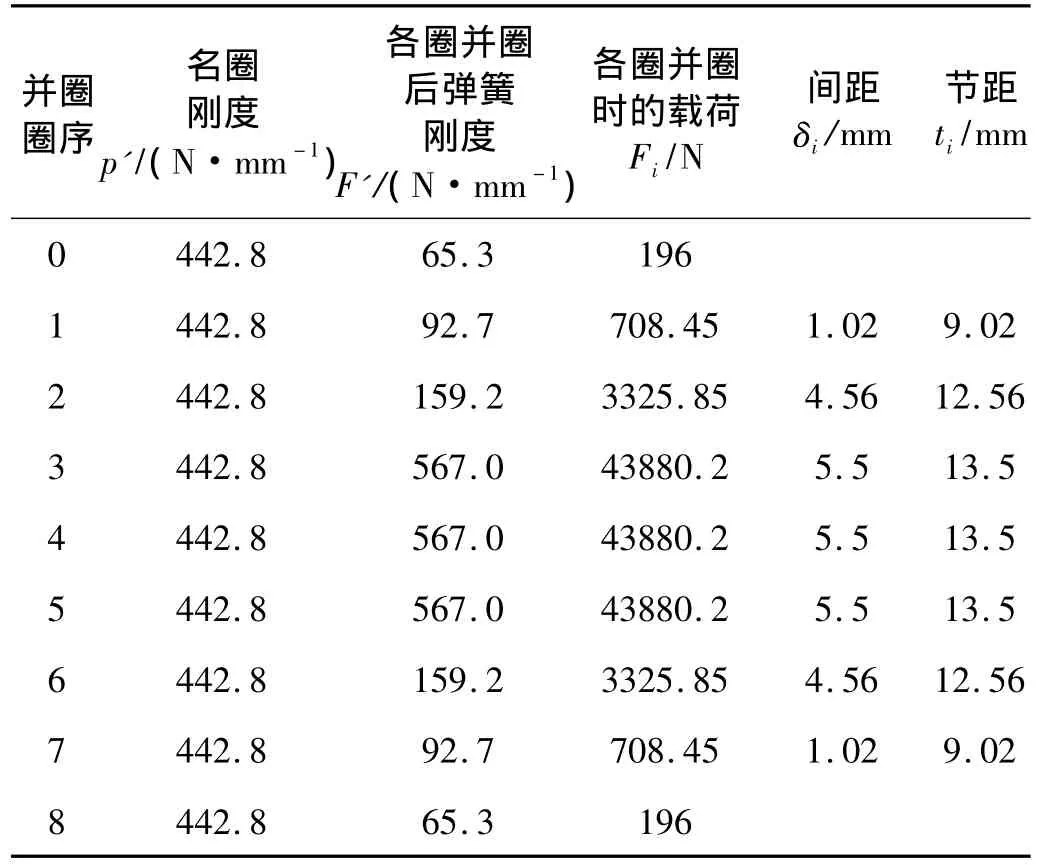
表1 弹簧设计计算主要参数表Tab.1 Main parameters for spring design and calculation

由表1可知，因节距为双向递增排列，故第2、6圈同时并圈时已满足最大工作载荷要求，为保证具有一定安全余量，以备突发状态下的特殊情况，3、4、5三圈的间距取值比2、6圈稍大；由于弹簧的各圈变形fi与各圈的间距具有如下关系：

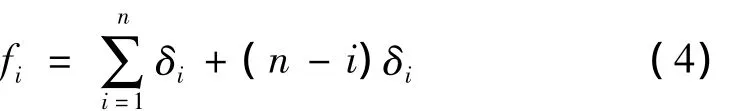
将表中数据代入式（2）、（4），可得修正后的弹簧载荷变形方程：

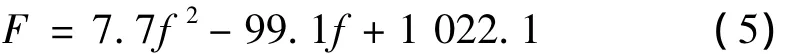
由式（3）、（5）可得修正前后两弹簧非线性硬特性线弹簧载荷与变形曲线，由表1可知，在一般载荷下系统变形随系统载荷增大而增加；当载荷突变增加到一定值时，即各圈并圈2圈以上时，系统变形随载荷增大而几乎无变化，呈现明显的硬特性非线性特征，这对增加振幅稳定性是有益的。

由表1将各圈并圈时刚度随载荷变化的规律绘成曲线，可知弹簧刚度-载荷曲线近似为一直线，即系统刚度与载荷基本呈线性关系。据此，可进一步说明硬特性非线性系统振幅的稳定性。

式（6）表示弹簧的自振频率，由式（6）可知，在变质量系统中，刚度与载荷为线性变化时，则ω仍为一常数，因该系统是在近共振状况下工作，而在近共振区附近其振幅Aa=F/（rω），由（6）式知ω基本为常数，r为系统的阻尼系数，变化也不大，若此时激振力F基本为常数，则Aa为常数，故近共振状态下振幅基本为常数，此时系统振幅稳定，工作状态平稳［6、18］。

样机研制发现，在系统出现的瞬态高振强作用下，不等节距螺旋弹簧的节距变化按由小到大递增单向排列时，一端并圈数较多而噪声较大，且对二级偏块系统引起载荷的阶跃变化反应敏感；节距变化按两端小中间大双向递增排列时，一端并圈数较少而噪声较小，且对二级偏块系统引起载荷的阶跃变化具有较大的适应性和稳定运转的鲁棒性；本设计采用后者是考虑到高振强的影响及系统工作稳定性。

非线性变节距弹簧使系统刚度随载荷变化而变化，不但具有节能高效之特点，同时能使系统振幅基本稳定。故将传统振动磨中作为主振弹簧的普通螺旋压缩弹簧改为适宜的非线性变节距螺旋压缩弹簧，可达到稳定系统振幅、实现系统高效节能之目的。为进一步降低噪声，将橡胶涂层涂覆在变节距螺旋金属弹簧表面，制成变节距螺旋金属橡胶涂层复合弹簧，橡胶采用百分之八十以上天然胶的合成胶制作而成，达到减振、降噪、耐磨的目的［12］。

3 隔振系统机理及分析

如图1所示，隔振弹簧在下质体与底板之间，采用橡胶帆布夹层复合材料，设计为环形橡胶弹簧结构，简称橡胶弹簧，与下质体及底板均采用动销定位。

非线性隔振系统的研究和应用，受限于非线性动力学的研究进展［19-20］，研究隔振系统的载荷-变形特性中的非线性特性，是因为隔振系统的非线性在高振强、大振幅情况下的隔振效果是非常显著的，在低振强、小振幅情况下，线性与否得到的隔振效果相差不大，故在某些可能产生高振强、大振幅情况下，须将非线性的影响考虑其中。如当系统承受瞬态高振强激励时，主振系统需引入硬特性线非线性弹簧系统，隔振系统则用具有大阻尼的非线性环形橡胶复合弹簧，能有效的吸收主振弹簧的强振，并能产生次谐波隔振等非线性效应，同时系统中出现附加的坐标耦合，可产生隔振所需要的、随载荷而变化的系统变刚度特性，研究表明通过下列指标最小化可以使系统具有最优的动态特性［20］：

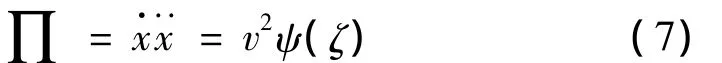
在高振强激励下，非线性隔振系统中会出现次谐波振动、超谐波振动和混沌振动现象，若应用适当，能起到较好的隔振效果。样机的隔振弹簧设计主要考虑系统采用变频调速时，主振系统振幅变化增加，振动强度显著提高，应如何减少主振系统振动对地基的传递。

根据系统的载荷情况，经分析与试验后决定选用端部为大圆角的环形橡胶复合弹簧，变形以压缩为主，受压后的静刚度可由下式计算：

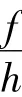
由式（8）及试验分析可知：系统的隔振弹簧采用环形橡胶复合弹簧，易实现理想的非线性特性，弹簧的弹性变形随载荷增减而增减，且具有高内阻，对突加载荷、高振强、超高振强、大振幅的吸收及与基础的隔振效果良好，使得系统传到地基上的力和同规格的单质体振动磨相比，锐减85%；且由于橡胶帆布夹层复合材料的作用，隔振弹簧可同时承受多向载荷，使用寿命长，安装维护便利。

4 振动测试分析

研制的振动磨样机主要技术参数：磨筒直径150 mm；中心高850 mm；总体尺寸800×550×900 mm3；激振源EZD-10-4型振动电机；功率0.55 kW；振次1 460次/min；混合介质球半径r∈［1-5］，介质充填率0.77、物料充填率0.08。

将d（0.5）：10 μm 金刚石粉体及磨介置入样机筒体，振动力幅值调至16 kN，振强设为 6～22，利用变频编程控制振动实验。

样机运行时，利用Brüel＆ Kjaer公司的振动测量仪器-PULSE多谱分析仪系统以及测试分析软件PULSE Labshop version 8.0，对样机的相关量进行测试和分析，在上下质体上分别设置6、4个测点，各测点的布置方法如图2所示，A、B、C、A'、B'、C'6个测点被布置在上质体上，同理D、E、D'、E'4个测点被布置在下质体上。检测分为三个阶段，分别为：振动磨的开机阶段、运行阶段和停机阶段。测得运行某时刻上下质体的加速度时域曲线和功率谱曲线如图3～图14所示。

由图3～图8可以看出，非线性振动带来的系统输出加速度时域变化特性：启动阶段，上质体在4 ms时，瞬间通过低阶共振点，加速度幅值为1 200 m/s2，此时下质体加速度幅值为200 m/s2，相差6倍，足见隔振之作用与效果；运行过程中，上质体加速度幅值大幅变化频次少、中小幅变化频次多，变化幅值在100-800 m/s2之间，恰满足振动磨在超微粉碎时，对瞬态高振强的需求，亦表明主振系统的非线性作用效果，拟籍此解决微细颗粒的解团聚，而此时的下质体加速度幅值变化明显减弱，显然是橡胶复合弹簧对强振的衰减效应；停电后，上质体加速度幅值经历惯性延续，通过低阶共振点后逐渐衰减，而下质体由于停电前的强振传递时滞，加速度幅值反以较大变化振荡后衰减［20］。

噪声功率谱密度是结构在类随机动态载荷激励下振动噪声响应的统计结果。测得上下质体的噪声功率谱密度如图9～图14所示，可从中解析噪声功率密度随频率变化的规律，进而分析系统的主隔振性能与状态。

由图看出，由于主振与隔振系统的非线性，使得上下质体功率谱曲线均呈现类随机性，上质体在启动初期出现较高的噪声功率密度，随后随频率增大而减小；运行中噪声功率谱分布曲线时有峰值出现，在频率段5～6 kHz达到最大值，它表达了噪声与引起这种噪声的振动现象的内在关系，有助于研究瞬态高振强的具体过程；停机时上质体的功率谱曲线则随频域增加而正常衰减。

下质体在启动阶段噪声功率密度变化幅值明显高于上质体，随后显著减弱；运行中噪声功率谱分布曲线普遍较上质体为弱，表明隔振系统具有较好的吸振效果；停机阶段噪声功率密度变化幅值较上质体稍高，亦表明是对主振系统通过低阶共振点时的响应，而后随频域增加而迅速衰减。

由上述分析知，加速度的大幅变化机率虽少，却可使得振动系统瞬态振强明显提高，用于振动磨样机恰可达到微纳颗粒解团聚与增加粒度细化的效果，使获得相同粒度的振动时间较常规振动明显缩短，工作效率明显增加。

5 试验与检测

在振动磨样机上对超细粉体进行粉磨试验，筒体内放入粒度为10 μm的人造金刚石粉体颗粒及一定比例的介质，将振动强度设在某区间变化，且进行变频编程控制试验，采用间断式振动粉磨，累计运行200 h，可获得开机前后在JSM-6360扫描电镜上的扫描图像。

图15为在MS2000激光粒度仪上对样粉进行粒度分布检测的结构图，图中可知粉体颗粒达d（0.5）：0.175μm，证实了此非线性系统不仅可进行超细超微磨作业，粒度细化，且能明显提高生产能力，缩短粉碎时间，使物料在筒体内用较短的工作时间获得较好的磨碎效果。应当注意的是：此时振动频率不宜太高，适当的振动频率不仅是降低磨粉能耗所希望的，而且对轴承寿命也极为有利，颗粒的解团聚尚有进一步提高的余地。

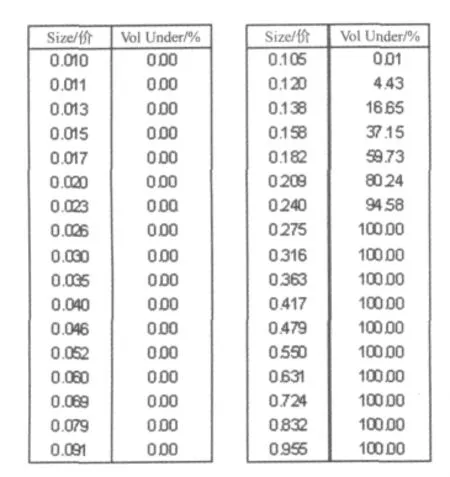
图15 激光粒度仪的粒度分布检测结果Fig.15 Size distribution of test results on laser particle size analyzer

从试验结果可以看出：适度地调整此非线性系统的一些主要技术参数，必定可以获得更好地解团聚、更细的粉碎粒度，直至达到纳米级水平。

6 结论

（1）研究在可产生瞬态高振强的二级偏块振动磨中，主振系统采用非线性硬特性线变节距橡胶涂层复合弹簧，使其刚度具有随动载荷即振动强度变化而变化的特性，以适应系统瞬态高振强的作用，达到系统稳定工作、节能高效的目的；采用环形橡胶复合弹簧作为隔振系统的隔振弹簧，使系统具有高内阻，一方面可实现对主振弹簧通过下质体传递的瞬态高振强的有效吸收，一方面又起到下质体与地基良好的隔振效果；

（2）通过二级偏块振动磨样机的振动试验，测得系统的加速度时域曲线和功率谱曲线，分别显示出主振与隔振系统的非线性作用效果。

（3）对超硬粉体进行超细超微粉碎获得的成功，使得其它硬质、脆性材料的微纳化变得相对简单，一方面可为其它硬质、脆性材料的微纳化提供借鉴，并将在此基础上较容易地研发出脆性材料微纳化经济、实用的解决办法；一方面可使超硬和其它脆性材料粉体的纳米颗粒粉碎制备成为可能，使人类向粉碎法低成本获得高质量纳米颗粒及超硬纳米颗粒的目标又迈进一步。

［1］郑水林，黄 朋，陈俊涛.超细粉碎与精细分级技术现状及发展［C］.银川：第八届全国颗粒制备与处理学术和应用研讨会，2007.8.

［2］冯 锐.我国超细粉碎机械的研究进展［J］.硫磷设计与粉体工程，2008，5：13-17.

［3］王秦生.超硬材料及制品［M］.郑州：郑州大学出版社，2006.

［4］Bernotat S.Vibration mill results in the light of stress intensity and number of stressing events［J］.Mineral Processing，2004，74：119-122.

［5］张世礼.特大型振动磨及其应用［M］.北京：冶金工业出版社，2007.

［6］Zhang Y M，Wang S，Liu Q L，et al.Reliability analysis of multi-degree-of-freedom nonlinear random structure vibration systems with correlation failure modes［J］.Science in China Series E-Technological Sciences，2003，46（5）：498-508.

［7］ Lou J J，Zhu S J，He L，et al.Application of chaos method to line spectra reduction［J］.Journal of Sound and Vibration，2005，286（3）：645-652.

［8］刘极峰，杨小兰，邹景超.新型高振强双质体振动磨的非线性振动［J］.机械工程学报，2008，44（7）：190-194.

［9］杨小兰，刘极峰，朱大胜，等.多级偏块单筒振动磨［P］.中国201010119944.2.2011-07-20.

［10］Amick H，Bayat A.Meeting the vibration challenges of new photolithography tools［J］.Journal of Sound and Vibration，2002，36（3）：22-24.

［11］ Lang G F， SnyderD. Understanding the physicsof electrodynamics shaker performance［J］.Journal of Sound and Vibration，2001，35（10）：24-33.

［12］杨小兰.空间双质体非线性振动输送机的同步性［J］.农业机械学报，2007（1）：89-92.

［13］刘极峰，陈 旋，马履中.非线性振动烘干机之振动阻尼与振动同步［J］.农业机械学报，2007（2）：87-89，51.

［14］张英会.弹簧手册［M］.北京：机械工业出版社，2008.

［15］ Zhang Y M，Liu Q L，Wen B C.Dynamic research of a nonlinear stochastic vibratory machine［J］.Shock and Vibration，2002，9（6）：277-281.

［16］韩清凯，罗 忠.机械系统多体动力学分析、控制与仿真［M］.北京：科学出版社，2010.

［17］徐 波，王树林，李生娟.振动磨碎机动力学分析及仿真试验［J］.机械工程学报，2008，44（3）：105-109.

［18］金栋平，胡海岩.碰撞振动与控制［M］.北京：科学出版社，2008.

［19］Rivin E L.Passive vibration isolation［M］.New York：ASME Press，2003.

［20］朱石坚，楼京俊，何其伟，等.振动理论与隔振技术［M］.北京：国防工业出版社，2006.