橡胶隔振器加速疲劳试验谱的编制方法研究
陈 芦,鲍雨梅,潘孝勇,段小成
(1.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,杭州 310004;2.宁波拓普集团股份有限公司,宁波 315806)
橡胶隔振器的疲劳试验通常采用室内模拟试验。室内模拟试验一般采用经验载荷谱或道路载荷谱(下文简称路谱)进行疲劳试验。路谱较经验载荷谱能够更真实的反应出橡胶隔振器的实际寿命。然而,如果完全施加实测的道路载荷,将会占用大量的试验时间和人力。因此,加速零部件的疲劳试验,节省产品的寿命验证时间,有着重要的工程实际意义。
总体来说,国内对于金属类线性材料制品的疲劳研究相对比较成熟,但是对橡胶或橡胶-金属相结合的非线性类制品的疲劳研究还刚起步,而对该类制品的加速疲劳试验谱编制方法的研究更是滞后于国际水平。现阶段,国内大多数的疲劳试验还采用经验载荷谱,有些虽然采用了道路载荷谱,也不能合理地进行编辑,不能准确地反映零部件的实际使用寿命[1]。国外一些汽车厂通过对采集的路谱进行编辑,使编辑后的载荷谱与原始路谱对橡胶隔振器产生的损伤分布及损伤值基本一致,而且较大程度地缩短了疲劳试验时间。然而,对外公开发表的资料较少。
本文以某发动机悬置(下文简称悬置)的路谱为研究对象,应用雨流计数法[2-3],充分考虑填充型橡胶材料的动静态特性[4-5],依据 Miner线性损伤累积理论[6]和损伤等效原则[7-8],建立了悬置的加速疲劳试验谱的编制方法,其编制流程如图1所示。
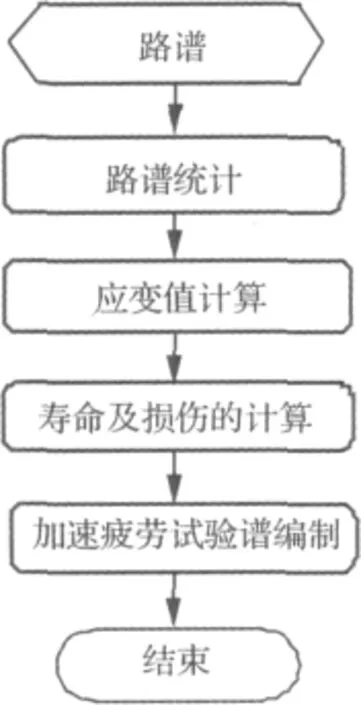
图1 加速疲劳试验谱编制流程图Fig.1 Flow chart of editing accelerative fatigue test spectrum
1 路谱统计
路谱由汽车试验场采集所得,试验道路覆盖了车辆使用过程中可能遇到的各种工况路面。
本文采用雨流计数法对路谱作统计。分析所有工况路面的载荷谱,提取最大峰值和最小谷值作为雨流计数的上限值和下限值,按一定间隔将路谱划分为多个载荷块(Fda,Fdm),其中,Fda为路谱载荷幅值,Fdm为路谱载荷均值。雨流计数过程在疲劳分析软件nSoft中进行。图2为悬置路谱的雨流计数直方图。

图2 路谱的雨流计数直方图Fig.2 Rain-flow counting histogram of road spectrum
2 应变值的计算
2.1 动静比数据表的建立
与一般的粘弹性材料一样,橡胶材料也存在动态特性。一些学者的研究表明:橡胶材料的动刚度随着激振振幅的增大而减小,即振幅相关性或称Payne效应;随激振频率的增大而增大;随温度的升高而减小[4-5]。但是,这些研究并没有获得各因素之间的具体变化关系,以至于不能准确获得橡胶隔振器的动刚度,进而无法准确得知橡胶隔振器在路谱作用下所产生的位移值或应变值。(若未作特别说明,则文中所述应变皆指危险点处的最大对数主应变,并定义:零件受拉时的最大对数主应变为正,受压时的最大对数主应变为负。)如何将路谱载荷转化为橡胶隔振器的实际位移值或应变值是橡胶隔振器加速疲劳试验谱编制过程中的一个难点。
对此,文中作如下处理:先不考虑温度的影响,并假设当振幅和预载一定时,在整个加载过程中,橡胶隔振器的静刚度和动刚度保持不变。于是,设Ks和Kd分别为橡胶隔振器在某一振幅和预载作用下的静刚度和动刚度,使其产生相同位移所需的对应静态力和动态力分别为Fs和Fd。则:

令:

则有:

其中:R称为动静比。
对橡胶隔振器进行有限元静态分析,通过数据拟合得到ε0-Fs(应变-力)函数关系:

综上可知,只需获得橡胶隔振器的动静比R,就能由式(3)计算得静态力,进而由式(4)计算出相应的应变值。为了准确获得橡胶隔振器的动静比,本文提出以下动静比实验获取方法。
以哑铃形试件(见图3)为试验对象,进行动静态性能实验。试件的材料为填充橡胶,硬度 HS50,试验设备为MTS831弹性体测试机,试验温度为常温。
以Mooney-Rivlin模型为橡胶材料的超弹性本构模型,进行有限元分析,读取有限元分析的力和应变数据并拟合得到力-应变曲线。试验时,以该力-应变曲线为依据,对试件施加一定的力以产生相应的应变。

图3 哑铃形试件结构图Fig.3 Structure of dumbbell-specimen

图4 动刚度与频率的关系曲线Fig.4 Curve of dynamic stiffness and frequency
图4为哑铃形试件的动刚度与频率的关系曲线,由图中可知,橡胶材料的动刚度受频率的影响较小,其上下偏差在5%以内。同时,由于路谱的激振频率主要集中在1~20 Hz,而图4的频率范围为1~50 Hz,覆盖了路谱的主要频段。因此,动态实验时以5Hz为激励频率,对应的刚度值作为橡胶隔振器的动刚度。准静态试验的加载速度为0.01 mm/s,取该加载速率的刚度值为橡胶隔振器的静刚度。于是,由式(2)可得橡胶隔振器的动静比。
通过大量的动静态试验,整理数据后,最终获取了HS50的填充橡胶材料的动静比数据表。表1为动静比随应变幅值和应变均值变化的二维数据表,其应变幅值变化范围为 0.02 ~0.5,间隔值为 0.02;应变均值变化范围为 -0.5 ~0.5,间隔值为 0.05。

表1 动静比数据表Tab.1 Data sheet of dynamic-static ratio
2.2 悬置的有限元分析
图5为悬置的有限元网格模型。约束面为金属外管,加载面为金属内管;使用刚性连接单元关联到中间一点,并以该点为加载点施加位移激励;读取悬置加载点的反力值及危险点的应变值,拟合可得如式(4)形式的应变-力函数关系。

图5 悬置有限元网格模型Fig.5 Mount mesh model
2.3 应变值的计算方法
由2.1节可知,计算应变值必须首先求得动静比,但是表1却是关于应变幅值和应变均值的动静比数据表,在应变未知的情况下是无法求得动静比的,这就形成了逻辑上的矛盾。对此,文中通过插值法不断循环逼近的方式实现动静比的求解,进而达到计算应变值的目的。应变值的计算在MATLAB中进行,计算流程如图6所示。
由于路谱载荷为动态力,无法直接使用式(4),于是,假设路谱载荷为静态力(下文简称拟静态力),则代入式(4)可求得悬置在该拟静态力作用下所产生的拟应变值,再由表1经插值可得到拟动静比R1,结合式(3),求得假想情况下的静态力。再次将该静态力代入式(4),求得第二次拟应变值,并插值计算出第二次拟动静比R2,反复循环将使动静比不断增大并收敛,当前后两次拟动静比的相对偏差ei满足设定值(一般取ei<1%)时,退出循环,并取最后一次拟动静比Ri作为实际动静比R。其中,

图6 应变值计算流程图Fig.6 Flow chart of strain calculate

确定动静比之后,结合式(3)和式(4),可计算各个路谱载荷块(,)对悬置零件产生的实际应变值。计算公式如下:

3 寿命及损伤的计算
3.1 寿命数据表的建立
同样以哑铃形试件为试验对象,进行大量的疲劳试验,该试件的结构及胶料配方与动静态试验的试件结构及胶料配方相同。每个应变工况做6个试件,取平均值作为该应变工况的寿命值。试验结果的Haigh图显示见图7,其中,Emin为应变谷值,Emax为应变峰值,颜色由黑到红代表寿命不断增大。收集疲劳试验数据,整理、并拟合出多条不同循环特性下的应变-寿命曲线。其中,零循环比时,应变峰值与寿命的关系曲线如图8所示,图8坐标为双对数坐标。零循环比应变-寿命曲线为:

图7 疲劳寿命Haigh图Fig.7 Haigh diagram of fatigue life

以图7为依据,结合上述拟合的多条不同循环特性下应变-寿命曲线,同时参考Mars等[9-10]的关于疲劳影响因素的研究内容,对部分未进行疲劳试验的应变循环的寿命值进行扩展计算。最终,建立了HS50填充橡胶的单轴寿命数据表,如表2所示。
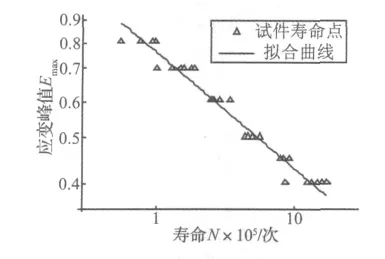
图8 零循环比时的应变-寿命曲线Fig.8 Train-life curve under zero cyclic ratio
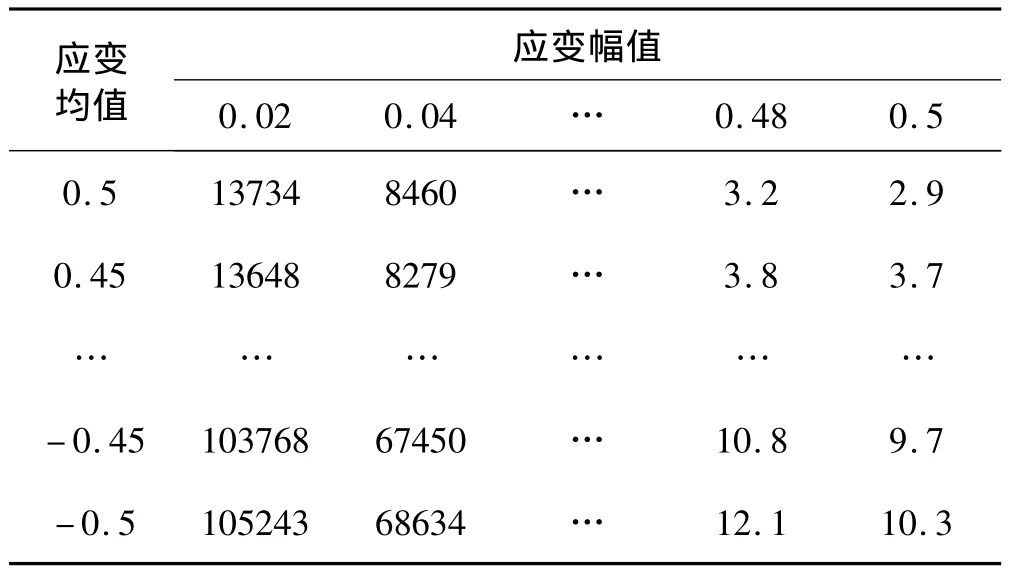
表2 寿命(万次)数据表Tab.2 Data sheet of life(104cycle)


其中,要求公式右侧多项式的截距为1。式(9)建立了非零循环比向零循环比的转换关系,再结合式(8)可实现不同循环比的寿命计算。理论上,图7划分的越细,公式(9)的数目越多,计算结果也将更准确,在此不作累述。
3.2 各载荷块的寿命及损伤的计算
结合1.2节的雨流计数结果,计算各路谱载荷块所产生的损伤值,图9为悬置路谱的损伤直方图。损伤的计算公式如下:

其中,j为路谱载荷块编号;Dj表示路谱载荷块j引起的损伤值;nj表示路谱载荷块j出现的次数;Nj表示路谱载荷块j单独加载时的寿命值。
根据工程上常用的 Miner线性损伤累积理论(即零件在各个载荷块下的疲劳损伤是相互独立的,总损伤是可以线性叠加的),求得悬置在整个路谱作用下的总损伤D,计算公式:

图9 路谱的损伤直方图Fig.9 Damage histogram of road spectrum

4 加速疲劳试验谱的编制
根据损伤直方图,选取5个典型载荷块进行加速疲劳试验谱的编制。典型载荷块是指损伤值最大的5个载荷块。设编制后的加速疲劳试验谱总循环次数为Nx,基于损伤等效理论,按比例合理分配循环次数,使5个典型载荷块所产生的总损伤与原始路谱所产生的总损伤相等,即:

其中,k为典型载荷块的编号;αk是典型载荷块k的疲劳试验的循环次数比例系数;Nx是加速疲劳试验谱的总循环次数;αkNx表示加速疲劳试验时,典型载荷块k的循环次数;Nk是零件受典型载荷块k作用时的寿命值。由下式决定,即:

其中,nk是典型载荷块k的雨流统计循环次数。
以文中的悬置路谱为例,由图9确定其5个典型载荷块(单位:N)分别为(750,-125)、(1 550,-875)、(1 650,-875)、(1 650,-1 125)和(1 750,-1 125)。联立式(12)和式(13),计算出悬置加速疲劳试验谱的总循环次数Nx为174 899次,5个典型载荷块的循环次数分配情况见表3。表3中的编号1、2、3、4、5分别依次代表上述5个典型载荷块。

表3 典型载荷块循环次数分配表Tab.3 Distribution of cyclic times for typical load block
为减少典型载荷块的集中出现,在编排载荷序列时,将总循环次数Nx平分为10份,任选一份进行编排,所得载荷序列称为子序列。疲劳试验时,按照子序列重复加载,直至断裂失效。若以5 Hz的频率进行加速疲劳试验,则加速疲劳试验只需9.72 h,而路谱的试验时间总和为215.82 h,可见,加速疲劳试验时间较原始路谱的试验时间较大程度地缩短了试验周期。图10为编制后的加速疲劳试验谱子序列示意图。
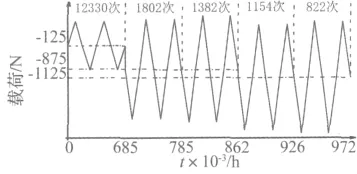
图10 加速疲劳试验谱子序列示意图Fig.10 Sketch map of sub-sequence of accelerative fatigue test spectrum
5 疲劳试验与结果分析
悬置的加速疲劳试验和路谱疲劳试验的测试系统均为MTS810疲劳试验机,试验温度均为室温,试件数分别为3个和2个,装夹方式如图11所示,试验结果如表4所示。
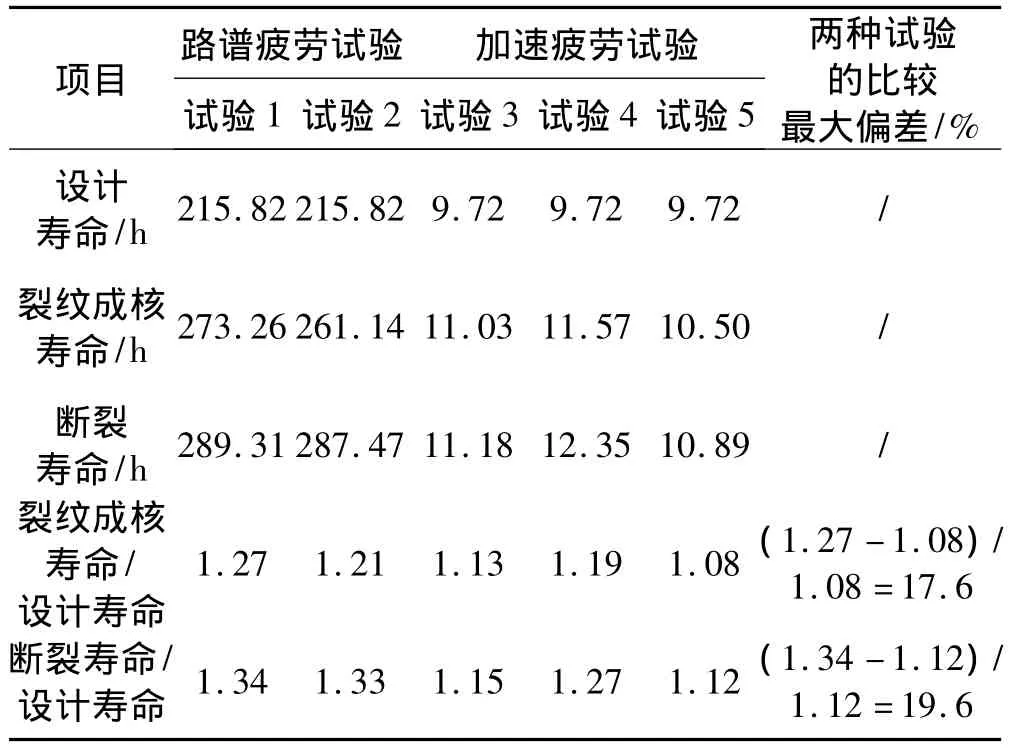
表4 疲劳试验记录表Tab.4 Notes of fatigue test

图11 疲劳试验工装Fig.11 Fixture of fatigue test
由表4可知,路谱疲劳试验的裂纹成核寿命是其设计寿命的1.27和1.21倍,断裂寿命是其设计寿命的1.34和1.33倍;加速谱疲劳试验裂纹成核寿命是其设计寿命的1.13、1.19 和1.08 倍,断裂寿命是其设计寿命的 1.15、1.27 和 1.12 倍。不难发现,两种疲劳试验对悬置的裂纹成核寿命和断裂寿命存在一定的当量关系。虽然,其当量关系的最大偏差值分别达到为17.6%和19.6%,但是,其偏差值也表明:加速疲劳试验的整个寿命历程(包括裂纹成核和裂纹扩展)有80%以上是与路谱疲劳试验相一致的,基本反映了悬置的实际寿命状况,满足工程实际应用。
图12为加速疲劳试验与路谱疲劳试验的失效裂纹示意图。比较图12(a)和图12(b)可知,加速疲劳试验谱与路谱对悬置的失效位置和断面形状基本一致。
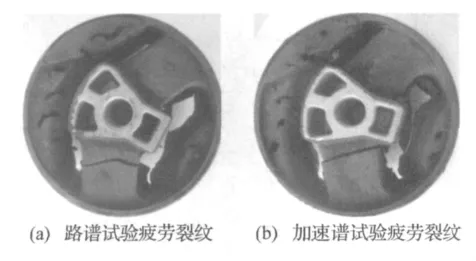
图12 疲劳裂纹的比较Fig.12 Comparison of fatigue crack
综上,加速疲劳试验与路谱疲劳试验,两者的寿命历程及疲劳裂纹(包括失效位置和断面形状),都是相一致的。因此,用文中所述方法编制的加速疲劳试验谱可成功应用于悬置的加速疲劳试验。
6 展望
(1)探讨了橡胶隔振器的应变值计算方法,并通过实验的方式建立了HS50填充橡胶的动静比数据表,该数据表可用于不同结构的橡胶隔振器。
(2)探讨了橡胶隔振器的损伤计算方法,并通过实验的方式建立了HS50填充橡胶的寿命数据表,该数据表同样可用于不同结构的橡胶隔振器。
(3)综合考虑了橡胶隔振器的动静态特性、寿命评价方法等,建立了橡胶隔振器的加速疲劳试验谱的编制方法。试验结果表明:该方法编制的加速疲劳试验谱较大程度地缩短了试验时间,可成功应用于橡胶隔振器的加速疲劳试验。
7 结论
(1)文中在加速谱的编制过程中,将路谱频率以5 Hz进行了统一处理;未考虑试验过程中的升温对动静比及损伤的影响;寿命试验覆盖范围不够广,覆盖密度不够大,以至寿命数据表不可避免的存在误差,这些都会影响加速疲劳试验谱与实测路谱的一致性。这些有待于今后的工作继续完善。
(2)文中只对单轴加速疲劳试验谱进行了研究,对于多轴加速疲劳试验谱的编制,需要考虑各轴向载荷的相位关系,这部分内容的研究将使橡胶隔振器的加速疲劳试验谱更加贴近实际路谱,具有非常重要的工程应用价值。
[1]王 进,左国兵.疲劳试验在橡胶减振制品寿命预测中的应用[J].铁道车辆,2005,4(7):7-10.
[2]Olagnon M,Guede Z.Rainflow fatigue analysis for loads with ultimodal power spectral densities[J].Marine Structures,2008,21(2-3):160-176.
[3]王国军,胡仁喜,陈 欣.nSoft疲劳分析理论与应用实例指导教程[M].北京:机械工业出版社,2007.
[4]潘孝勇.橡胶减振器动态特性计算与建模方法的研究[D].杭州:浙江工业大学,2009.
[5] Sjöberg M.On dynamic properties of rubber isolators[D].Sweden:Doctoral Thesis,MWL,KTH,2002.
[6]尚德广,王德俊.多轴疲劳强度[M].北京:科学出版社,2007.
[7]赵勇铭,宋迎东.基于损伤等效的多轴疲劳试验谱编制研究[J].航空动力学报,2009,24(9):2026-2032.
[8] Aberg S,Podgorski K,Rychlik I.Fatigue damage assessment for a spectral model of non-gaussian random loads[J].Probabilistic Engineering Mechanics,2009,24:608-617.
[9] Mars W V.Factors that affect the fatigue life of rubber[J].Rubber Chemistry and Technology,2004,3(77):391-412.
[10] Saintier N,Cailletaud G,Piques R.Multiaxial fatigue life prediction for a natural rubber[J].International Journal of Fatigue,2006,28:530-539.

