失谐叶盘结构振动响应局部化实验研究
廖海涛,王 帅,王建军,李其汉
(1.中国航空研究院,北京 100012;2.北京航空航天大学 能源与动力工程学院,北京 100191)
失谐周期结构中存在的振动局部化现象通常包含两个方面[1-2]:一是由失谐周期结构固有特性所反映出的模态局部化,二是由结构的响应特性所反映出的振动传递局部化,振动响应局部化的理论分析文献评述及定量评价指标可参考文献[3-4]。与理论计算进行对比印证是实验研究中的重要环节,特别是对于各种失谐方法进行实验验证更是不可或缺的。在失谐叶盘结构响应局部化实验研究方面,国外学者做了开创性的工作,例如,Kruse[5]采用压电陶瓷作动器作为阶次激励激振装置,测量了高密度模态区域阶次激励作用下的强迫响应特性。而 Judge[6-7]通过在各叶片尖部粘贴不同的质量块实验研究了频率转向区域以外高密度模态弱耦合区域的失谐叶盘振动模态局部化和强迫响应振幅放大。Duffield[8]采用飞轮激振形式进行了阶次激励下发动机风扇叶盘简化模型的稳态强迫响应实验研究,Jones和Cross[9]使用激光振动测量仪研究了叶尖位置的叶盘结构强迫响应局部化,通过实验验证了相对于失谐而言,激振误差对振动响应只会引入很小的变化。基于Jones设计的行波激振装置和平板叶盘结构模型,Kenyon 和 Griffin[10-11]用实验演示了失谐幅值放大系数达到最大值的叶盘结构响应局部化现象并研究了局部化响应的鲁棒性能。Ibrahim[12]研究了叶片失谐和叶片凸肩阻尼对叶盘结构稳态响应的影响并提出了一种测量旋转状态下叶片振动响应的方法。而国内关于失谐叶盘结构强迫响应实验处于空白状态。不仅如此,由于试件结构的复杂性、实验系统环境和仿真功能的局限性等因素的限制,失谐叶盘结构的响应局部化实验有待深入开展。
为了达到实验与理论结果具有定量可比性的目的,本文应用文献[3-4]所提出的方法,首先对具有12个叶片的平板叶盘结构进行有限元仿真以确定失谐叶盘响应局部化失谐方案,基于行波激励叶盘结构的实验系统测量了失谐叶盘结构的强迫响应,后经过数据采集与后处理程序得到响应数据,最后通过比较失谐叶盘有限元数据与实验结果分析了叶盘结构强迫响应局部化及其特性。
1 实验系统及测量方法
本文的整体叶盘结构行波激励响应实验测量系统实物如图1所示。主要包含四个部分:行波激振系统,实验对象,激光振动测量系统,数据处理系统。其简要的工作流程为:由装有PCI模拟输出卡和利用Lab-VIEW软件开发的“行波激振信号发生系统VI”的数控计算机来产生和控制行波激振所需的交变电压信号,对于本叶盘模型共需13路交变电压信号,经由PCI-6723模拟输出卡和SCB-68端子板输出满足要求的电压模拟信号后,将分别接入压电陶瓷驱动电源和拾振系统:其中12路作为压电陶瓷动态驱动电源(需3台)的输入控制信号,另1路则提供给拾振系统作为参考信号。将12路控制信号接入动态驱动电源后,可通过调节旋钮来调节和控制各个输出通道输出相同幅值的交变电压,最后将保真放大后的交变电压接入压电陶瓷激振器来激励实验件。由激光振动测量系统拾振,然后综合必要的采集数据完成后处理。具体原理可见文献[13]。

图1 整体叶盘结构响应特性实验系统实物图Fig.1 Overall experimental setup of the excitation and measurement system
实验主要研究整体叶盘结构试件的稳态响应特性,因此采用步进式的行波激励方式。即每次用一个频率给出行波激励信号,测出该激励的稳态响应,再步进到下一个频率,直到所有预先设定的频率离散点全都步进完毕。实验研究目的在于定量研究失谐对叶盘结构试件振动响应幅值的影响,这里选择1阶弯曲模态族作为响应特性实验研究频率范围,在叶盘试件每个叶片的尖部布置一个测点(共12个)作为实验模型,各测点的测量方向均为轴向(Z向)。该实验测量模型保证了所关心的结构点都在所选的测量点之中,而通过各个测量点的振幅及相位关系,也足以胜任在变形后明确显示在实验频段内的所有稳态响应的变形特征及各响应间的变形区别。
2 信号采集和数据处理
对于每个频率点的测量,实验模型各测点包含激励信号(参考信号)和响应信号两路信号的采集与记录。对于参考信号来说,由于难以采集到压电陶瓷片所产生的力信号,这里是用压电陶瓷动态驱动电源第1个通道(共12个通道)的输入控制信号来替代激励信号,直接由行波激振系统中的SCB-68端子板输出提供,为指定频率下的正弦交变电压信号(单位:V);振动响应主要采集的是速度信号(单位:m/s),两路信号均由激光振动测量系统采集记录,采样信号的处理过程分为四部:① 剔除速度响应信号中存在的明显奇异项;② 消除大于数据采样周期的趋势项;③ 采用五点三次平滑法平滑速度信号并用梯形求积积分方法转换为位移信号;④ 求解互功率密度函数。测量信号采集记录中的关键参数及信号处理具体过程可参考文献[13]。
3 数值仿真与实验验证
为了对实验试件模型特征及其激振实施手段同时进行有效的模拟,理论计算采用了ANSYS软件的直接耦合场压电分析功能。失谐叶盘结构试件的有限元模型如图2所示,叶盘模型各叶尖处为失谐质量块,各质量块结构几何尺寸相同,而通过改变密度来控制其质量,用改变质量块的密度来模拟失谐,叶片根部为压电陶瓷激振片,采用的是耦合场SOLID5六面体单元划分,对其上下表面节点分别进行了电压(VOLT)自由度耦合,并施加行波谐激励电压,采用了单组分有机绝缘硅胶(回天HT903)提高绝缘性以降低各激振器间的干扰。计算中电压幅值取为40V,阻尼系数取为0.001,失谐强度均取为0.05。该模型共15 888个单元,26 088个节点,模型几何尺寸、材料属性可参考文献[13]。

图2 失谐叶盘结构试件理论计算有限元模型Fig.2 Finite element model of the blisk
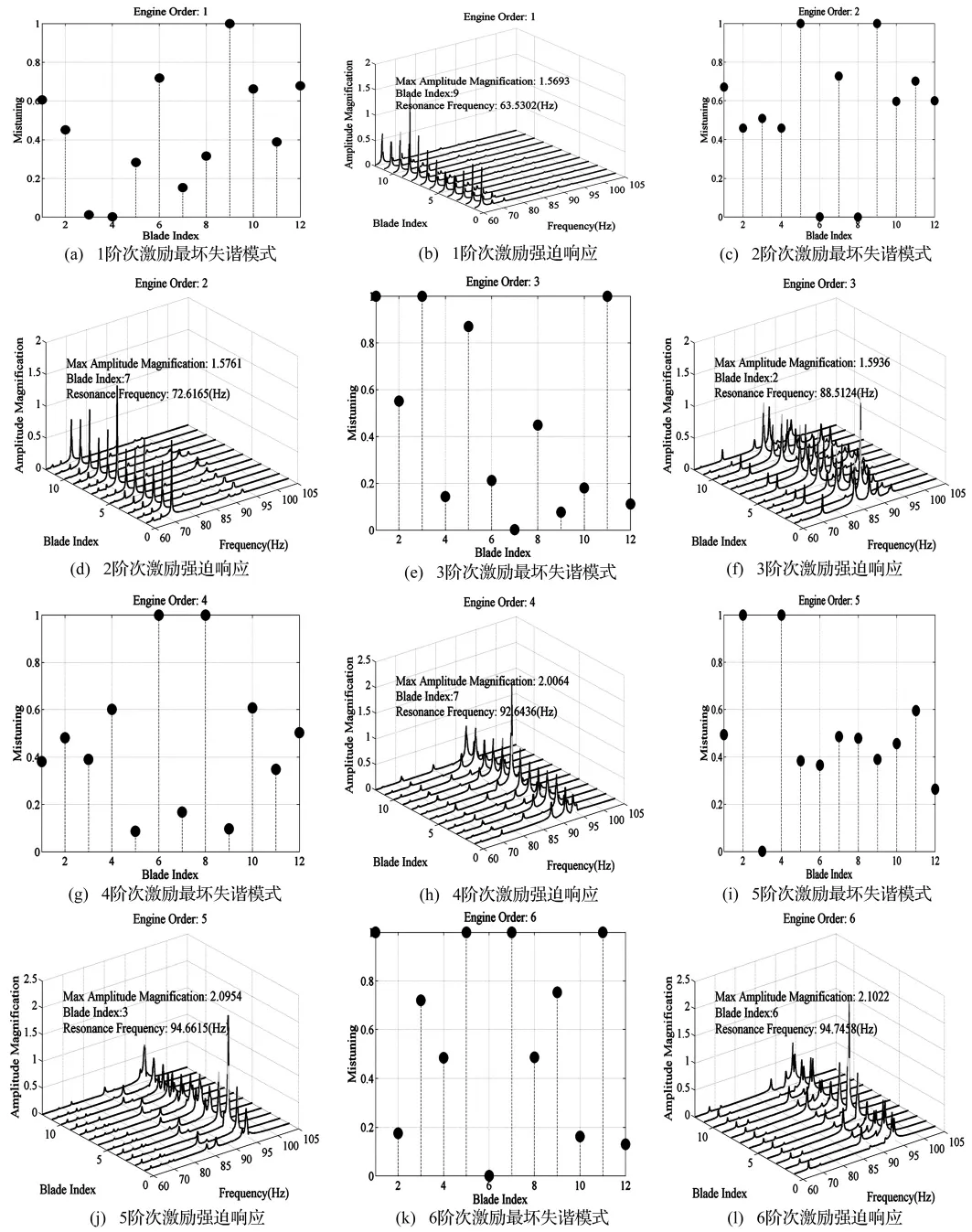
图3 不同阶次激励下叶盘结构最坏失谐模式及其强迫响应特性Fig.3 The worst mistuning patterns and its forced response of the bladed disk by different engine order excitation(EOE)
图3给出了对应于1至6阶次激励作用下有限元仿真计算得到的最坏失谐模式及相应的频率响应曲线。由图可知,对应不同的阶次激励,与最大共振峰值对应的共振频率逐渐升高,而且随着阶次激励的增大,幅值放大系数逐渐增大,但是在5和6阶次激励,其有限元仿真共振频率均在94 Hz附近,它们的幅值放大系数相对于其它阶次激励是最大的,而这两者之间近乎相等,说明叶盘结构对激励敏感程度降低了。此外,在最坏失谐模式中失谐值之间的变化差异程度随着阶次激励的增大而变得更为剧烈,特别是在5和6阶次激励最坏失谐模式中3和6号叶片的失谐变量值为0,与两侧的失谐变量值(为1)形成了极大的反差,由相应的频响特性可知,这两个叶片位置共振峰值是最高的。说明最坏失谐模式中失谐跳变与频率响应曲线的幅值放大作用是正相关的,即最坏失谐模式失谐跳变越明显,则相应频率响应模式中叶片强迫响应局部化越强烈。
有限元理论仿真表明在各个阶次的行波激励下,失谐叶盘试件最坏失谐模式在激励频率范围均出现了不同程度的共振峰,特别是对于5和6阶次激励最坏失谐模式,理论仿真的频响曲线显示其幅值放大系数高达2.1,振动能量分别集中在3和6号叶片,发生了强烈的响应局部化现象,因此本文实验也主要以相应5和6阶次行波激励最坏失谐模式来研究失谐叶盘试件的稳态响应振幅放大。表1列出了实验5和6阶次激励最坏失谐模式所添加失谐质量块质量。实验测量得到的固有频率如表2所示,由表可知这两种失谐模式除了中间第6、7、8阶模态的固有频率不同,其它阶模态的固有频率均很接近,特别是第10、11、12阶模态几乎一致,从图4给出的5和6阶次激励最坏失谐模式第12阶局部化模态振型可以看出,分别对应着3#和6#叶片位置出现了模态局部化,模态能量高度集中,这两种失谐模式实验测量得到的固有频率非常接近,但相应的模态振型却显著不同,说明叶盘的一弯模态族对失谐非常敏感,此外,同图3比较可知,最坏失谐模式的失谐值在相同的叶片位置发生了跳变并在有限元仿真频响曲线中伴随着强烈的响应局部化现象。
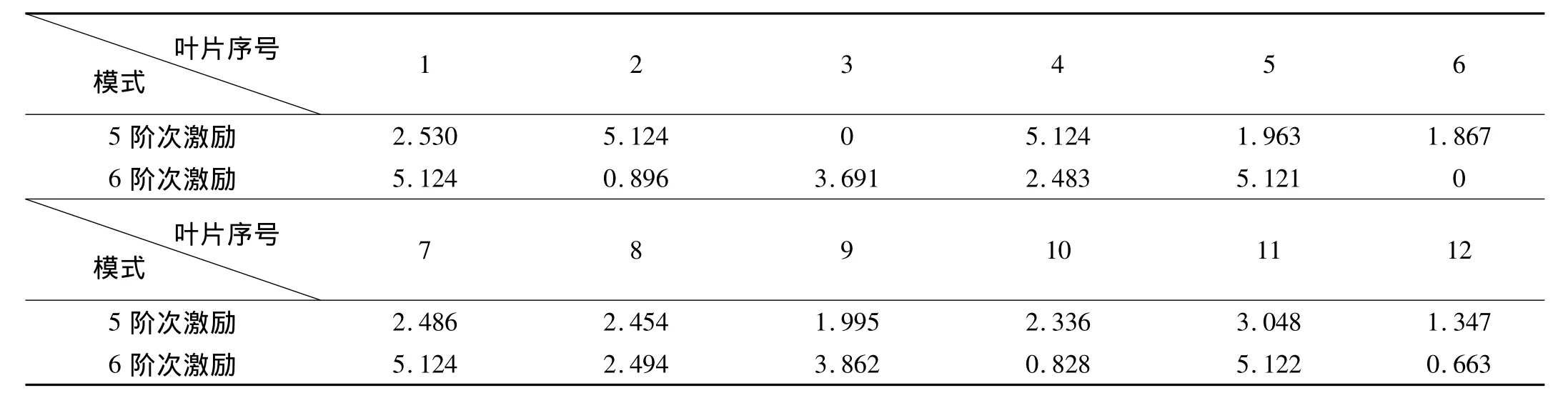
表1 5和6阶次激励添加质量块的质量(单位:g)Tab.1 Mass added to the tip of blade of the validation blisk

表2 5和6阶次激励最坏失谐模式固有频率实验测量结果Tab.2 Eeperimental natural frequencies of the worst case mistuning patterns
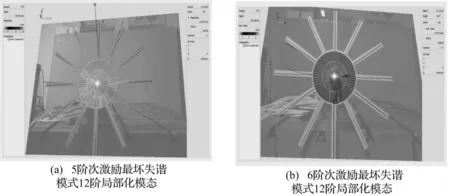
图4 5和6阶次激励最坏失谐模式实验测量局部化模态Fig.4 Localized mode shapes of validation blisk measured by the psv
采用上述的步进激励法来测量频响函数,其精度主要在于设定合理的频率步长。本实验中对各个阶次的行波激励实验均采用相同的频率步长设定是不现实的,因此依据阶次激励、叶盘结构试件模态特性等因素特点制定了各自相适应的步长设定方案,总的原则是在测试过程中采用了不等距步长,在远离共振频率的地方曲线变化缓慢,步长取得较大,通常取为0.5 Hz(最高为1 Hz),在各共振峰的位置步长取得较小,通常取为0.1 Hz。由图5给出的6阶次行波激励下最坏失谐模式失谐叶盘试件的行波激励实验频响曲线可知,相对于理论谐调系统,共振峰值出现分离,而且在各阶模态频率区域均出现了一定程度的共振峰,特别是在8阶~12阶模态区域激发出了很强的强迫响应,这与谐调叶盘受到行波激励后强迫响应仅出现在单个节径的模态振型区域是具有显著区别的。由于激励频率测量点较多,对于5阶次行波激励下最坏失谐模式叶盘试件只在一弯模态族12个实验固有频率点附近测量了其频响特性(步长0.1 Hz)。实验测量结果与理论计算得到的5和6阶次激励失谐模式最大响应振幅发生的位置是相同的,即分别为3号和6号叶片的尖部,发生了强烈响应局部化。图6显示了相应峰值频率下,失谐叶盘最高幅值叶片(即3号和6号叶片)的响应分布模式,从中可以看出,对应于5和6阶次激励下最坏失谐模式的响应,3号和6号叶片的振幅分别为其最大值,其分布规律在理论仿真与实验结果对比关系中体现出一致性,实验测量与理论计算得到了较好相互印证。
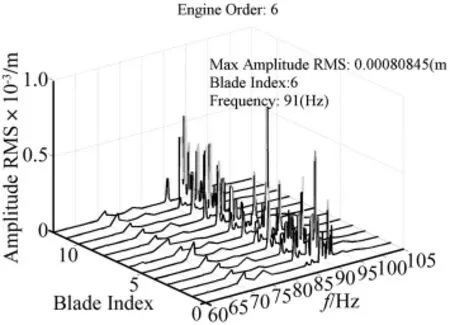
图5 6阶次激励最坏失谐模式叶盘结构实验测量强迫响应特性Fig.5 The experimental forced response of the blisk by EOE6

图6 不同阶次激励最坏响应模式实验结果与有限元仿真比较Fig.6 Comparision of the worst response patterns between the experimental results and the FEM predictions
比较图4与图6中出现强烈模态和响应局部化的叶片位置,发现在5和6阶次激励作用下均是激励出了第12阶局部化模态振型,这与振动理论是吻合的,说明叶片强烈的振动响应局部化必要条件是叶片出现了模态局部化,但是与最坏的模态局部化没有对应关系,因为叶片的强迫响应水平不仅取决于失谐模式,而且与激励模式和阻尼水平等因素有关。由于失谐叶盘的每一阶模态包含了所有阶次节径的成份,在每一阶次的行波激振下,叶盘结构的各阶固有频率区域均会依照该阶失谐模态振型所包含的相应阶次的简谐成分量级作出相应的稳态响应[5]。由此可知,5和6阶次激励最坏失谐模式的12阶局部化模态振型中占主导地位节径成份分别为节径5和6。
4 结论
针对循环对称结构系统,尤其是发动机转子整体叶盘结构失谐振动实验研究的需求,设计提出了一种行波激励实验系统,该系统表现为一系列软硬件的集合,可在转子叶盘保持静止的状态下,对其在真实工作运行环境中所承受的阶次激励进行有效的且易于在实验室实现的模拟。提供了一套完整的整体叶盘结构行波激励稳态响应的振动测量方法、采集信号处理方法、仿真与实验结果对比方法。
针对典型整体叶盘结构,本文实验研究了失谐叶盘结构与最坏失谐模式对应的振动响应局部化现象,基于文献[3]的理论分析方法预测了不同阶次激励作用下实验平板叶盘结构有限元模型的最坏失谐模式并确定了实验方案,通过实验验证了失谐跳变-局部化这个理论发现,实验测量与理论计算结果在定量的层面上得到了较好相互印证。
最坏失谐模式中某些叶片失谐值变化剧烈,在该区域位置叶盘结构模态和响应对失谐均非常敏感,而失谐叶盘结构的局部化响应水平与结构的几何形状、阻尼、失谐模式以及激励水平等因素有关,其本质主要取决于两个条件:一是失谐模态的节径谱与行波激励的节径谱的相似程度,当激励节径谱与振型节径谱相似程度很高时,系统接受激励能力很强,就会出现很强的响应局部化现象;二是被激起模态的局部化程度,模态局部化是产生失谐叶盘结构响应局部化的必要而非充分的条件。前者反映了系统接受外界激励能量的能力,后者反映了系统自身的固有属性对于失谐的敏感程度。两者的共同作用造成失谐叶盘结构幅值放大,叶片的强迫响应对特定阶次激励作用非常敏感,较之名义谐调叶盘,失谐叶盘试件的失谐量较大,失谐量的增加通常会引起各阶失谐模态振型包含更加丰富的节径成份,这将大大增加该模态被各个阶次的行波激励有效激发的概率。
[1]王建军,李其汉,朱梓根.失谐叶片-轮盘结构系统振动局部化问题的研究进展[J].力学进展,2000,30(4):517-528.
[2]Castanier M P,Pierre C.Modeling and analysis of mistuned bladed disk:status and emerging directions[J].Journal of Propulsion and Power,2006,22(2):384 396.
[3] Liao H T,Wang J J,Li Q H.Mistuning forced response characteristics analysis of mistuned bladed disks[J].ASME Journal of Engineering for Gas Turbines and Power,2010,132(12):122501-01/11.
[4]廖海涛,王建军,李其汉.随机失谐叶盘结构失谐特性分析[J].航空动力学报,2010,25(1):160 -168.
[5] Kruse M J,Pierre C.An experimental investigation of vibration localization in bladed disks,part II:forced response proc[C].42nd ASME Gas Turbine and Aeroengine Cong.,1997,Orlando,Florida,USA.
[6] Judge J,Pierre C,Mehmed O.Experimental investigation of mode localization and forced response amplitude magnification for a mistuned bladed disk[J].Journal of Engineering for Gas Turbines and Power,2001,123:940 -950.
[7] Pierre C,Judge J,Ceccio S L,et al.Experimental investigation of the effects of random and intentional mistuning on the vibration of bladed disks[C]//Proceedings of the 7th National Turbine Engine High Cycle Fatigue Conference,Universal Technology Corp,Dayton,OH,2002.
[8] Duffield C J,Agnes G S.An experimental investigation on periodic forced vibrations of a bladed disk.AIAA -2001-1668,2001.
[9] Jones K,Cross C.A travelling wave excitation system for bladed disks[C].43rd AIAA/ASME/EASCE/AHS/ASC Structures,Structural Dynamics and Materials Con,AIAA 2002 -1531,2002,Denver,Colorado.
[10] Kenyon J A,Griffin J H.Experimental demonstration of maximum mistuned bladed disk forced response[J].ASME Journal of Turbomachinery,2003,125:673 -681.
[11] Kenyon J A.Robust maximum forced response in mistuned turbine engine bladed disks[D].Pittsburgh:Carnegie Mellon University,2002.
[12] Ibrahim Ata sever.Experimental validation of turbomachinery blades vibration predictions[D].London:Imperial College London,2004.
[13]王 帅.整体叶盘结构失谐识别方法及动态特性实验研究[D].北京:北京航空航天大学,2010.

