分谱处理算法在基于超声导波损伤识别中的应用
苗晓婷,李富才,孟 光
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
近20年内,超声导波(如兰姆波)已被广泛应用于无损健康检测领域[1-4]。基于超声导波的损伤识别方法通常是把试件无缺陷时所采集的波信号作为基准,并把当前所采集的检测波信号与基准波信号进行对比,从而提取出由损伤散射的波信号的特征信息,如飞行时间(ToF)等[5-6],达到损伤识别和定位等目的。由于超声导波不可避免的频散特性以及工作环境中的噪声严重降低了检测波信号的信噪比(SNR),很难依据原始的检测波信号评估出损伤散射的波信号的ToF。因此信号处理技术对基于超声导波的损伤识别起到至关重要的作用,决定了ToF的精确评估以及三角定位算法的有效性。至今已有多种信号处理技术被广泛应用于提高信号的 SNR,比如 Hilbert-Huang变换(HHT)[7-8]和小波变换(WT)[9-10]。通过适当的降噪处理,可以直接把检测波信号与基准波信号相减以得到损伤散射的波信号,并基于能量分析方法评估出损伤散射的波信号的ToF[11-12]。然而在实际的工作环境中,检测波信号可能被不确定的噪声干扰,如果噪声能量分布在目标波信号的频率带内,此时通过HHT和WT仍然无法有效地排除噪声,噪声能量将淹没损伤散射的波信号的能量,导致这种基于能量分析方法的失效。
由于分谱处理(SSP)算法具有较好的抵抗随机噪声干扰的能力,它已被广泛应用于超声波的无损探伤和雷达定位[13-16]。当目标信号在所采集的信号中出现时,通过SSP算法所重建的一系列时间域信号将呈现出一致的幅值信息[17]。利用适当的特征提取算法,在各个采样时间点上提取这一系列重建的时间域信号的幅值并衡量它们的一致性,最终可以推断那些呈现出较好的幅值一致性的采样时间点对应于目标信号的出现。由于所衡量的幅值一致性不受噪声的影响,即使所采集的信号的SNR较低,SSP算法仍然可以正确地评估目标信号的ToF。
本研究分别在无噪声和有噪声干扰检测波信号的情况下利用SSP算法评估铝板中的切缝缺陷所散射的基础阶对称(S0)模式的ToF。结合传感网络中各条激励-传感路径所评估的ToF,最终利用三角定位算法在传感网络所包围的检测区域内识别并定位切缝缺陷。
1 基本原理
1.1 基于ToF的三角定位算法
在被用于损伤识别的波信号的特征信息中,ToF是比较直观的特征信息之一。利用三角定位算法,结合传感网络中各条传感路径所评估的损伤散射波信号的ToF,可以在传感网络所包围的检测区域内识别并定位缺陷[18-19]。薄板结构中的超声导波——兰姆波包括两种模式,即对称模式与反对称模式,并且不同的模式各自以不同的速度在板内传播。对板结构而言,在任何激励频率下至少会有两种模式的兰姆波被同时激励出来并在结构中传播。通过调整激励的中心频率,可以使结构中传播的模式降低到最少,即基础阶的对称(S0)和反对称模式(A0)[20]。在这种情况下,由于 S0模式具有最快的传播速度,本研究通过评估损伤散射的S0模式的ToF来定位缺陷以避免波信号中其它波模式的干扰。由损伤散射引起的 S0模式的 ToF可以表示为:

其中:

TA-D-S是激发的S0模式从激励点传播到缺陷,再从缺陷传播到感应点所需要的飞行时间。TA-S是激发的S0模式从激励点直接传播到感应点所需要的飞行时间。LA-D是激励点(xA,yA)与缺陷的中心位置(xD,yD)之间的距离。LD-S是缺陷的中心位置与感应点(xS,yS)之间的距离。LA-S是激励点与感应点之间的距离。vg是S0模式的群速度。方程式(1)的解绘制出一个以激励点和感应点为焦点的椭圆,这个椭圆便是缺陷中心位置的坐标轨迹。结合传感网络中各条传感路径所评估的ToF,可以绘制出多条坐标轨迹,它们的交汇区域便是缺陷可能出现的区域。
1.2 分谱处理(SSP)算法
一般而言,一个原始信号r(t)包括目标信号s(t)和噪声n(t),可以表示为:

其中,T是信号的采样时间。信噪比(SNR)被用于衡量信号被噪声污染的程度,定义为[21]:

目标信号被噪声污染得越严重,SNR的值就越小。SSP算法包括两步:① 分谱;② 特征提取,算法流程如图1所示。
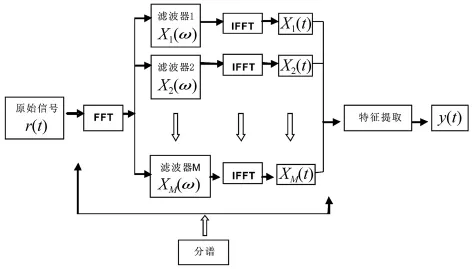
图1 SSP算法的流程图Fig.1 Schematic flow chart of SSP algorithm
1.2.1 分谱
(1)快速傅里叶变换(FFT)
利用FFT,可以获得原始信号r(t)的频率 -能量谱:

在本研究中,通过FFT所获得的能量谱的能量最大值(能量峰值)的一半所对应的起始频率和截止频率分别被用于指定信号的主要频率带,如图2所示。

图2 用于切分主要频率带的一组高斯带通滤波器的频率谱分布Fig.2 Frequency spectrum distribution of a series of Gaussian band-pass filters cutting the main frequency band
(2)带通滤波器
利用一组带通滤波器把所指定的主要频率带切分为一系列窄的频率带(Xi(ω),i=1~M),如图2所示。SSP算法的有效性与以下参数的合理选取有关:① 带通滤波器函数;② 带通滤波器的总数;③ 这一组带通滤波器的频率谱分布形式。本研究采用了总数为M的一组高斯带通滤波器,相邻两个带通滤波器的中心频率之间的频率间隔为Δf。它们各自具有不同的中心频率(fi,i=1~M),相同的带宽(2× Δf)。M个高斯带通滤波器把主要频率带切分为M个相互重叠的频率带以尽可能地减小信号成分的遗漏[22]。M和 Δf分别定义为:

其中T是信号的采样时间,即信号总的时间长度;B为主要频率带的带宽。
(3)傅里叶逆变换(IFFT)
所切分的M个窄的频率带(Xi(ω),i=1~M)各自进行傅里叶逆变换,重建了M个时间域信号:

本研究把xi(t),(i=1~M)的瞬时幅值的变化范围定义为信号r(t)的瞬时幅值变化度(IAVD(t)),表示为:
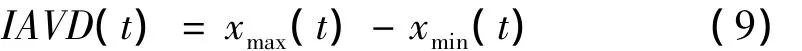
其中

如果xi(t),(i=1~M)的瞬时幅值在较小的范围内变化,则对应较小的IAVD(t)值;相反,则对应较大的IAVD(t)值。
1.2.2 特征提取
基于SSP算法的理论,当目标信号在所采集的信号中出现时,xi(t),(i=1~M),呈现出比较一致的瞬时幅值,对应较小的IAVD(t)值[14]。在以前的研究中,用于衡量瞬时相位一致性的特征提取方法(如极性阈值法和幅值最小值法)对SSP算法中所选用的带通滤波器的带宽以及频率谱分布形式比较敏感,这种敏感性在一定程度上降低了SSP算法的有效性[17]。本文所提出的特征提取方法是通过比较基准波信号的IAVD(IAVDbenchmark(t))和检测波信号的IAVD(IAVDdanage(t))来评估损伤散射的S0模式的ToF。当激励的S0模式或由损伤散射的S0模式在波信号中出现时,波信号的IAVD值较小。如果在某些采样时间点,IAVDbenchmark(t)的值较大,而IAVDdanage(t)的值较小,则意味着此时S0模式没有出现在基准波信号中却出现在检测波信号中,于是可以推断损伤散射的S0模式出现在这些采样时间点,并由此评估出损伤散射的S0模式的ToF。特征提取方法可具体描述如下:
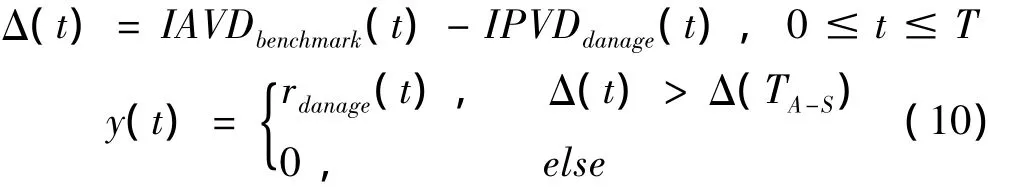
当激发的S0模式到达时(TA-S),IAVDbenchmark(t)与IAVDdanage(t)之间的差异(Δ(TA-S))被设定为阈值。在TA-S以后,如果 Δ(t)的值比 Δ(TA-S)大,则设定 SSP 算法在t时的输出(y(t))等于检测波信号rdanage(t)的幅值,否则设定y(t)的值为0。第一个值不为0的y(t)所对应的采样时间点被评估为S0模式从激励点传播到缺陷,再从缺陷传播到感应点所需要的飞行时间TA-D-S。把所评估的TA-D-S值代入方程式(1)中,则可以评估出缺陷散射的S0模式的飞行时间TD,并绘制出表示缺陷中心位置的坐标轨迹。
2 实验评估
2.1 实验装置
实验中利用一个基于VXI平台的信号发生和采集系统,以20.48 MHz的采样率采集波信号。这个系统包括:信号发生器(Agilent E1441)、信号放大器(Piezo-Sys EPA-104)、信号解调器(Agilent E3242A)和信号数字离散器(Agilent E1437A)。汉宁窗调制的、中心频率为300 kHz的、5周正弦调幅脉冲(峰峰值为60V)被用做激励信号激发板中的兰姆波。四个直径为6.9 mm、厚度为 0.5 mm的圆形压电应变片(PZT PI PIC151,PRYY-0929)被表面固定在铝板(600 mm ×600 mm ×2.0 mm)上,组成一个包围了400 mm ×400 mm大小的检测区域的传感网络,如图3(a)所示。利用一个坐标系来定位检测区域,它的原点设在P3,X轴由P3指向P4,Y轴由P3指向P1。选用了的六条激励-感应波信号的传感路径,各自采用“一发一收”的工作方式激励和采集兰姆波信号,覆盖了检测区域(图3(b))。实验中首先对无缺陷的铝板进行检测,并把所采集的波信号作为基本波信号。然后用一个厚度为0.6 mm的锯片在先前的铝板上切割出一条切缝缺陷,表格1详细列出了切缝缺陷的位置和尺寸。对带有切缝缺陷的铝板进行检测,并把所采集的波信号作为检测波信号。各个信号的采集时间均设定为200 μs。为了模拟嘈杂的工作环境,幅值大小不同的白噪声被分别加载到检测波信号上,相应地生成了具有不同信噪比的检测波信号。
2.2 实验结果与分析
在无缺陷的铝板中所测量到的S0模式在最短的传播路径(400 mm)上所需要的飞行时间TA-S为77 μs(第1 578个采样点),由此推算S0模式的传播群速度vg为5 195 m/s。下文举例展示对传感路径P3-P4所采集的波信号进行信号处理的过程。所采集的波信号进行统一的幅值正则化。

图3 (a)带有切缝缺陷的铝板与传感网络的示意图以及(b)所选用的六条传感路径Fig.3(a)Schematic diagram of the notched aluminum plate with a sensor network and(b)the six selected sensing paths

表1 铝板中切缝缺陷的位置和尺寸Tab.1 Notch in the aluminum plate
2.2.1 无噪声干扰时的损伤识别

图4 传感路径P3-P4所采集的基准波信号与无噪声干扰时的检测波信号Fig.4 The captured wave signals by sensing path P3 - P4 from benchmark and damage case without noise
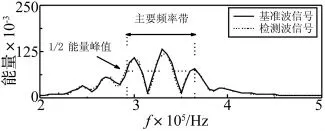
图5 基准波信号与无噪声干扰时的检测波信号的频率-能量谱Fig.5 Frequency-energy spectrum of the captured wave signals from benchmark and damage case without noise
无噪声干扰时,传感路径P3-P4所采集的基准波信号与检测波信号的幅值和相位之间存在一定的差异(图4),采样起始处的信号为电磁干扰。利用FFT,得到它们的频率-能量谱(图5)。对基准波信号而言,当频率为330 kHz时对应能量的最大值(0.13),能量峰值的一半所对应的起始频率为295 kHz、截止频率为365 kHz。因此所指定的主要频率带的带宽为70 kHz(从295 kHz到365 kHz),即:

对检测波信号进行分谱的过程中,指定与基准波信号相同的主要频率带(从295 kHz到365 kHz)。实验中所设定的采样时间为200 μs,即:

基于式(6)和式(7)可得:
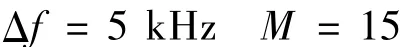
根据以上所设定的参数,本研究采用一组总数为15、相邻两个带通滤波器的中心频率之间的频率间隔为5 kHz、各自带宽为10 kHz的高斯带通滤波器,把基准波信号以及检测波信号的主要频率带切分成15个相互重叠的频率带(Xi(ω),i=1~15)。然后各自进行IFFT,重建了15个时间域的信号(xi(t),i=1~15)。图6举例展示了由基准波信号所重建的时间域信号x6(t),x7(t)和x8(t)。根据方程式(9)分别求得IAVDbenchmark(t)与IAVDdanage(t),如图7所示。根据方程式(10)分别求得Δ(t)和SSP算法的输出y(t),如图8所示;最终所评估的TA-D-S对应于第1 910个采样时间点(图8(b))。

图6 由基准波信号所重建的时间域信号Fig.6 The reconstructed time- domain signals(a)x6(t),(b)x7(t)and(c)x8(t)of the captured wave signal from benchmark

图7 所求得的基准波信号与检测波信号(无噪声干扰)的IAVDFig.7 IAVDbenchmark(t)and IAVDdamage(t)(without noise)

图8 无噪声干扰时的(a)Δ(t)和(b)SSP算法的输出y(t)Fig.8(a)Δ(t)and(b)the output of SSP algorithm(y(t))without noise
结合所选用的六条传感路径各自评估的TA-D-S,利用1.1节中所陈述的三角定位算法绘制出的缺陷中心位置的坐标轨迹的交汇区域如图9所示。把交汇区域中距离坐标轨迹的距离和最小的坐标识别为缺陷的中心位置坐标,所识别的中心位置以‘+’标记。表2中列出了所识别的中心位置坐标以及相对于实际中心位置的距离。

表2 在无噪声干扰和有噪声干扰(SNR=1 dB)时所识别的结果Tab.2 Identification results without and with noise(SNR=1 dB)

图9 无噪声干扰时所识别的缺陷位置Fig.9 Identified result without noise
2.2.2 有噪声干扰时的损伤识别
当检测波信号被幅值大小不同的白噪声干扰时,相应地,检测波信号的SNR分别为13 dB,8 dB,5 dB和1 dB,检测波信号被噪声污染得越严重,SNR的值就越小,如图10所示。利用SSP算法对SNR=1 dB的检测波信号进行处理。首先得到检测波信号的频率-能量谱(图11),相比于无噪声干扰时的检测波信号的频率-能量谱(图5)可以看出噪声能量严重干扰了检测波信号的能量,很大程度地改变了频率-能量的分布。对检测波信号进行如2.2.1节中所陈述的相同的信号处理,可以求得SNR=1 dB的检测波信号的IAVD,IAVDdamage(SNR=1dB)(图12),与图7比较可知在无噪声干扰时和SNR=1 dB时,所得到的检测波信号的IAVD基本一致。根据它与IAVDdenchmark(t)的差(图13(a))以及方程式(10)得到有噪声干扰时的SSP的输出y(t)(图 13(b)),最终所评估的TA-D-S对应于第1 930个采样时间点。可知在无噪声干扰时和有强噪声干扰时,利用SSP算法所评估的TA-D-S基本一致。同样结合所选用的六条传感路径各自评估的TA-D-S,绘制出的缺陷中心位置的坐标轨迹的交汇区域如图14所示。所识别的中心位置坐标以及相对于实际中心位置的距离如表2中所示。

图10 传感路径P3-P4所采集的具有不同SNR的检测波信号(a)SNR=13 dB,(b)SNR=8 dB,(c)SNR=5 dB和(d)SNR=1 dBFig.10 The captured wave signals by sensing path P3-P4 from damage case with noise(a)SNR=13 dB,(b)SNR=8 dB,(c)SNR=5 dB and(d)SNR=1 dB

图11 基准波信号与有噪声干扰时的检测波信号(SNR=1 dB)的频率-能量谱Fig.11 Frequency-energy spectrum of the captured wave signals from benchmark and damage case with noise(SNR=1 dB)
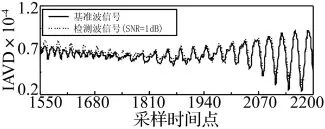
图12 所求得的基准波信号与检测波信号(SNR=1 dB)的IAVDFig.12 IAVDbenchmark(t)and IAVDdamage(SNR=1dB)(t)
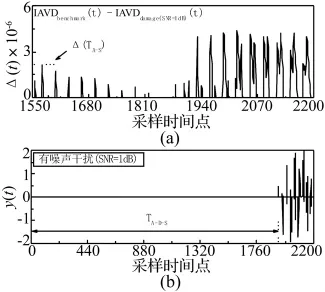
图13 有噪声干扰时的(a)Δ(t)和(b)SSP算法的输出y(t)Fig13(a)Δ(t)and(b)the output of SSP algorithm(y(t))with noise(SNR=1 dB)

图14 有噪声干扰时(SNR=1 dB)所识别的缺陷位置Fig.14 Identified result with noise(SNR=1 dB)
实验的损伤识别结果表明无论检测波信号是否被强噪声干扰,本研究所提出的SSP算法都可以精确地评估出损伤散射的S0模式ToF。所识别的缺陷中心位置的误差均小于33 mm(检测区域边长的8.25%),在允许的误差范围内。
3 结论
本研究提出一个SSP算法,通过比较基准波信号的IAVD与检测波信号的IAVD来评估损伤散射的S0模式的ToF。分别在理想(无噪声)和嘈杂(有噪声)的工作环境中检测带有切缝缺陷的铝板,利用SSP求得检测波信号的IAVD。并且通过适当的特征提取方法,与基准波信号的IAVD比较可以精确地评估出损伤散射的S0模式的ToF。结合传感网络中各条传感路径所评估的ToF,利用三角定位算法在传感网络所包围的检测区域内成功地识别出缺陷的位置。实验结果表明,无论检测波信号是否被强噪声干扰,利用本研究所提出的SSP算法所求得的信号的IAVD基本保持一致,进而保证在较低信噪比的情况下仍然能够精确地评估损伤散射的S0模式的ToF,实现有效的损伤识别与定位。本研究所证实的SSP算法强大的抵抗噪声干扰的能力,表明它在基于超声导波的损伤识别领域里具有很好的实用性。
[1]彭海阔,孟 光,李富才.一种基于压电晶片阵列的板结构损伤识别方法[J].振动与冲击,2009,28(9):56-59.
[2] Yang Y J,Cascante G,Polak M A.Depth detection of surface-breaking cracks in concrete plates using fundamental Lamb modes[J].NDT & E International,2009,42(6):501-512.
[3]Lu Y,Ye L,Su Z,et al.Quantitative assessment of throughthickness crack size based on Lamb wave scattering in aluminium plates[J]. NDT & E International,2008,41(1):59-68.
[4]张伟伟,王志华,宏 马.含缺陷管道超声导波检测信号的相关性分析[J].暨南大学学报:自然科学与医学版,2009,30(3):269-272.
[5] Wilcox P,Lowe M,Cawley P.The effect of dispersion on long-range inspection using ultrasonic guided waves[J].NDT& E International,2001,34(1):1-9.
[6] Li F,Meng G,Ye L,et al.Dispersion analysis of Lamb waves and damage detection for aluminum structures using ridge in the time-scale domain[J].Measurement Science and Technology,2009,20,095704:1 -10.
[7]Quek S T,Tua P S,Wang Q.Detecting anomalies in beams and plate based on the Hilbert-Huang transform of real signals[J].Smart Materials and Structures,2003,12(3):447-460.
[8] Zhang H,Fan S,Lu D.Application of Hilbert-Huang transform to arrival time extraction of multi-mode lamb waves[J].Journal of Vibration,Measurement and Diagnosis,2008,28(3):216-219.
[9]Li F,Meng G,Kageyama K,et al.Optimal mother Wavelet selection for lamb wave analyses[J].Journal of Intelligent MaterialSystems and Structures, 2009, 20(10):1147-1161.
[10]Ip K H,Tse P W,Tam H Y.Extraction of patch-induced Lamb waves using a wavelet transform[J].Smart Materials and Structures,2004,13(4):861-872.
[11] Jennifer E M.Detection,localization and characterization of damage in plates with an in situ array of spatially distributed ultrasonic sensors[J].Smart Materials and Structures,2008,17(3):1-15.
[12]Michaels J E,Michaels T E.Guided wave signal processing and image fusion for in situ damage localization in plates[J].Wave Motion,2007,44(6):482-492.
[13] Gustafsson M G.Nonlinear clutter suppression using split spectrum processing and optimaldetection[J]. IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1996,43(1):109 -124.
[14]Gustafsson M G,Stepinski T.Split spectrum algorithms rely on instantaneous phase information-a geometrical approach[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1993,40(6):659 -665.
[15] BenammarA, DraiR, Guessoum A. Detection of delamination defects in CFRP materials using ultrasonic signal processing[J].Ultrasonics,2008,48(8):731 -738.
[16] Roig I B,Domínguez L V.New insights and extensions of split-spectrum algorithms from an optimum distributed detection perspective[C].IEEE Ultrasonics Symposium,2005,1797-1800.
[17] Ericsson L,Stepinski T.Cut spectrum processing:a novel signal processing algorithm for ultrasonic flaw detection[J].NDT & E International,1992,25(2):59-64.
[18]Diamanti K,Soutis C,Hodgkinson J M.Lamb waves for the non-destructive inspection of monolithic and sandwich composite beams[J].Composites Part A:Applied Science and Manufacturing,2005,36(2 SPEC.ISS.):189 -195.
[19]Kessler S S,Spearing S M,Soutis C.Damage detection in composite materials using Lamb wave methods[J].Smart Materials and Structures,2002,11(2):269 -278.
[20] Santoni G B,Yu L,Xu B,et al.Lamb wave-mode tuning of piezoelectric wafer active sensors for structuralhealth monitoring[J]. JournalofVibration and Acoustics,Transactions of the ASME,2007,129(6):752-762.
[21] Karpur P,Canelones O J.Split spectrum processing:a new filtering approach for improved signal-to-noise ratio enhancement of ultrasonic signals[J].Ultrasonics,1992,30(6):351-357.
[22] Karpur P,Shankar P M,Rose J L,et al.Split spectrum processing:determination of the available bandwidth for spectral splitting[J].Ultrasonics,1988,26(4):204 -209.

