多管火箭发射过程中定向器振动特性研究
贺军义,芮筱亭,王国平,杨富锋,展志焕
(南京理工大学 发射动力学研究所,南京 210094)
射击精度差一直是制约多管火箭作战效能的瓶颈,射击精度差的根源是火箭弹起始扰动对多管火箭射击精度影响大。俄罗斯、美国、意大利、英国等国采用了简易制导火箭弹,如脉冲推力器控制[1],以提高多管火箭射击精度。简易制导火箭弹成本通常较无控火箭弹高许多倍,控制系统占用了弹箭的空间和质量,且简易制导不能根本上改变起始扰动对火箭弹射击精度的影响。Cochran在20世纪80年代提出了“被动控制”思想提高射击精度[2-3],而实现“被动控制”难度大,迄今尚未很好解决。国内外很多学者一直在对提高火箭炮的射击密集度进行大量的研究,潘宏侠等对火箭炮发射过程中的定向器的振动和火箭炮的密集度之间的关系进行了研究[4],文献[5]通过试验测试和联合时频分析对多管火箭定向器的振动特性进行了研究,从试验的角度对定向器的振动进行了初步的测试,文献[6]以螺旋导轨导旋的多管火箭发射系统为研究对象,发射装置振动对火箭弹初始扰动的影响,得到了因发射装置的振动对火箭弹所产生的初始扰动。如果在多管火箭炮上加装发射动力学控制系统,在火箭弹发射的过程中实时感测定向器姿态运动并控制定向器的姿态方位的变化,进而控制火箭弹的运动,减少火箭弹的起始扰动,使火箭弹主动段终点偏角大大减小,从而大幅度降低武器成本来提高多管火箭射击精度[7]。
多管火箭发射过程中对定向器振动实施有效控制的前提是要准确地测试和分析定向器管口的振动特性和运动规律,由于发射环境的复杂性,要想对定向器振动的角速率和线加速度信号的准确获取,必须设计合理设计信号采集处理系统,因此发射过程中定向器振动特性的研究显得非常重要。本文利用多体系统传递矩阵和发射动力学理论建立了刚弹耦合的多管火箭发射动力学模型和仿真系统,通过多管火箭模态试验验证了模型的正确性;仿真获得了在发射过程中定向器管口振动信号的时间历程,利用离散傅里叶变换(DFT)技术,获得了在发射过程中定向器管口振动位移、速度和加速度信号的频域特性;在此基础上设计了椭圆滤波器,并通过对发射过程中定向器管口的加速度采集信号的滤波前后对比,验证了本文研究的正确性和重要性,为多管火箭发射过程中定向器运动信号的采集和控制提供了重要参考价值。
1 多管火箭发射动力学模型
如图1所示,应用多体系统传递矩阵法[8],根据多管火箭武器的自然属性,将多管火箭武器划分成若干个元件。根据“体”和“铰”统一编号的原则,从地面到定向管口,各元件依次编号为0、1、2、…、23、17+7i、…、23+7i(i=1,2,…,40)。其中,7、8、9、10、11、12 代表车轮,元件19代表除去车轮的车体,元件21代表除去俯仰部分的回转部分,元件23代表除去已击发火箭弹和最新击发火箭弹所在定向管的起落部分,元件20+7i(i=1,2,…,40)代表最新击发火箭弹所在定向管尾部,元件 21+7i和元件 22+7i(i=1,2,…,40)分别代表前支撑框与后支撑框之间的定向管部分和前支撑框前面的定向管部分。多管火箭武器的发射动力学模型为在地面支撑条件和燃气流作用下的由各种铰相联接的44个刚体、40个弹性体和6个集中质量组成的刚弹藕合多体系统。
2 多管火箭发射动力学仿真系统及模态试验验证
2.1 多管火箭发射动力学仿真系统
根据文献[9]提供的方法,对某多管火箭炮系统进行了受力分析,利用多体系统传递矩阵法建立多管火箭发射动力学模型和计算,地面支撑已被包含在系统动力学模型中,这些系统内力均已在状态矢量中予以考虑,无需进行复杂而繁琐的受力表达,得到系统总体传递方程和特征方程为:
求解特征方程(2)可得到系统的固有振动频率ωk(k=1,2,…,∞),利用传递方程可得到对应ωk的状态矢量,从而可以进行多管火箭振动特性快速计算。在发射动力学模型的基础上,考虑定心部与定向管的接触力、角稳定系统控制力和力矩等因素,分别在火箭炮系和弹轴系建立火箭弹的质心运动方程和转动方程,非对称火箭弹在定向管内运动的一般发射动力学方程为:
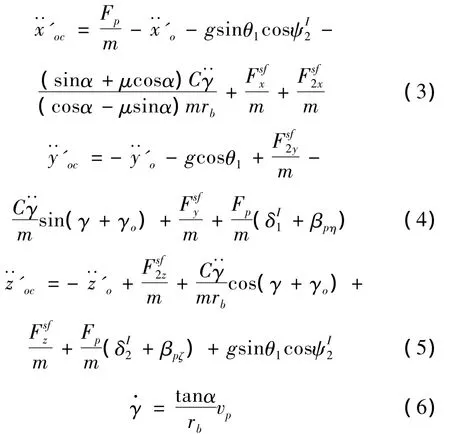
2.2 多管火箭仿真系统的模态试验验证
对多管火箭武器系统进行了振动模态试验,测试获得了多管火箭固有振动频率、振型、阻尼比等重要参数;同时利用建立的多管火箭发射动力学仿真系统对该多管火箭振动特性进行计算。表1列出了该多管火箭在40管满载情况下的仿真得到的前14阶固有频率与模态试验测试得到的前14阶固有频率,以及它们的相对误差。对比表明,两者吻合很好,模态试验验证了该多管火箭仿真系统的正确性。
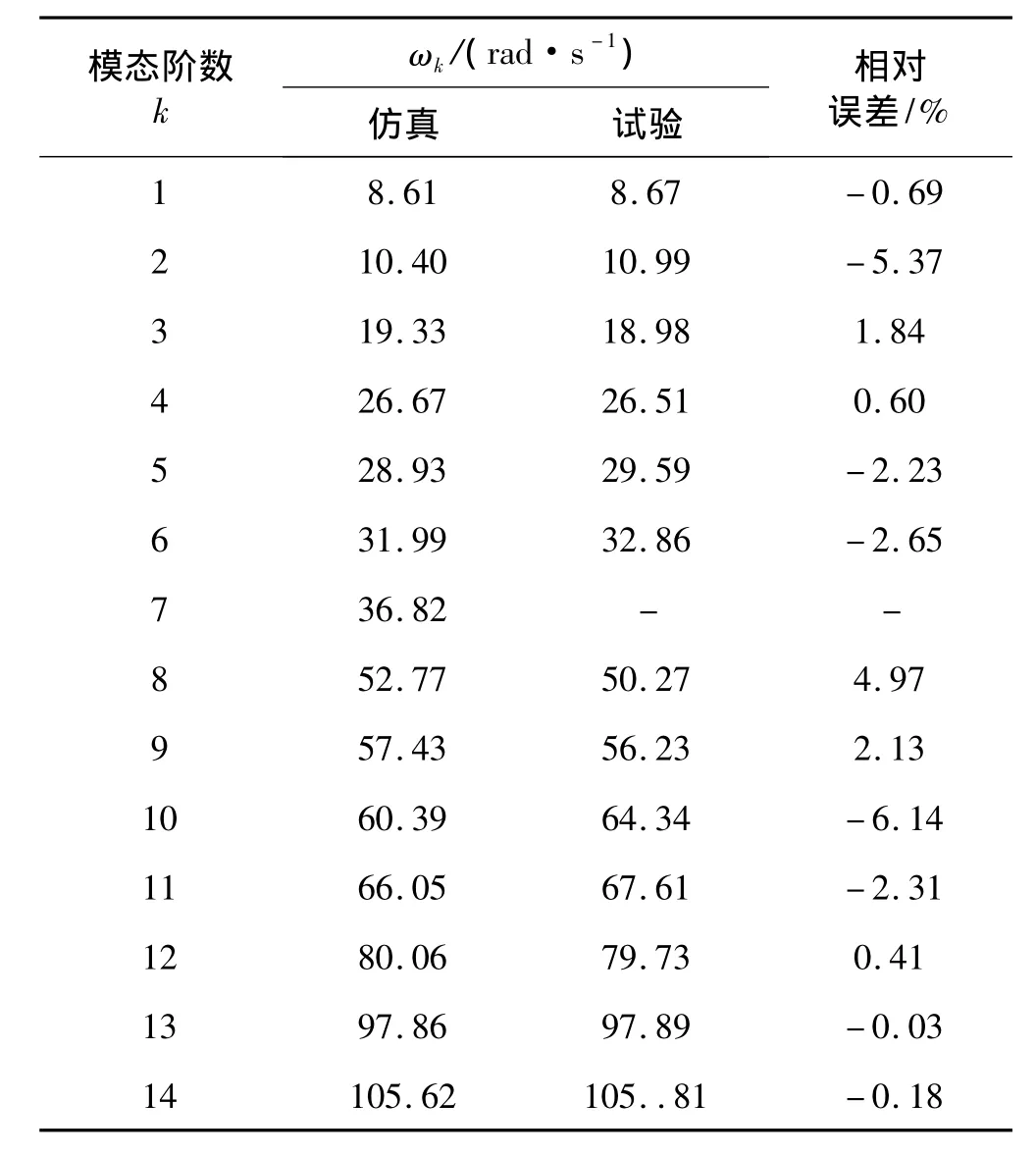
表1 满载情况下固有频率仿真与试验结果Tab.1 Comparison of simulation and modal test result of frequency in the circs of full-load
3 发射过程中多管火箭定向器振动特性的时频分析
3.1 发射过程中多管火箭定向器位移、加速度时域仿真研究
利用建立多管火箭发射动力学仿真系统,对某多管火箭在单发射击过程中的动力响应进行仿真,得到多管火箭定向器前箍处(管口处)的垂向和侧向的位移、速度、加速度等振动信号的过程曲线,其中垂向和侧向的位移、加速度仿真结果如图2、图3所示,仿真计算步长为 0.000 5 s。
3.2 发射过程中多管火箭定向器位移、加速度信号的频域分析
一般离散序列x(n)的离散时间傅里叶变换DTFT[10]为:
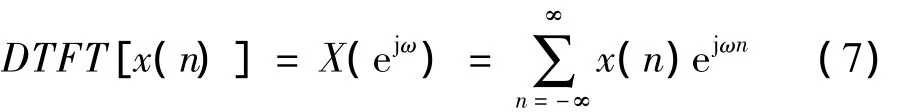
而序列x(n)不仅可以进行DTFT,也可以进行离散傅里叶变换(DFT),序列的DFT正是利用计算机实现进行序列频谱分析的前提。一个离散周期序列x(n)(任意有限长序列都看做是周期序列的主值序列)的DFT为:
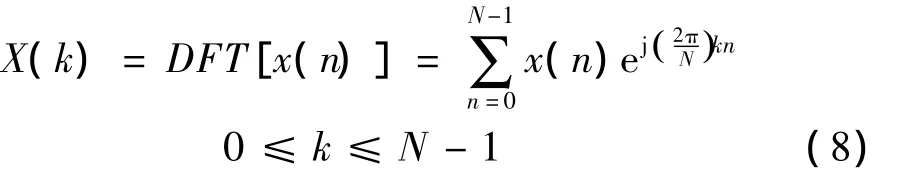
根据离散信号的DFT变换理论,利用MATLAB编程工具,对得到的位移、加速度等离散时间信号进行DFT变换,获得了多管火箭单发射击的过程中,定向器前箍处垂向和侧向位移、速度、加速度等信号的频域特性,其中垂向和侧向位移、加速度信号的频域特性如图4、图5所示。由频谱特性可知,定向器前箍处垂向的信号的频带明显比侧向要宽,而且垂向和侧向位移信号的频带较低,一般在100 Hz以内,而速度的频带范围相对较宽,一般在250 Hz左右,加速度的频率组成最丰富,频带较宽,高频信号对它影响很大,在滤波器设计和处理时要综合考虑,根据不同的采集任务,设计不同滤波器带宽对采集任务的顺利完成至关重要。
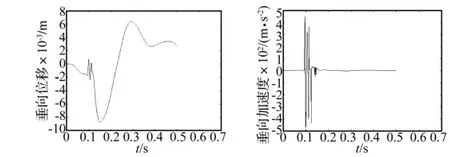
图2 发射过程中定向器前箍处的垂向的位移、加速度时间历程Fig.2 Time history of displacement and acceleration in vertical direction at launch guider muzzle
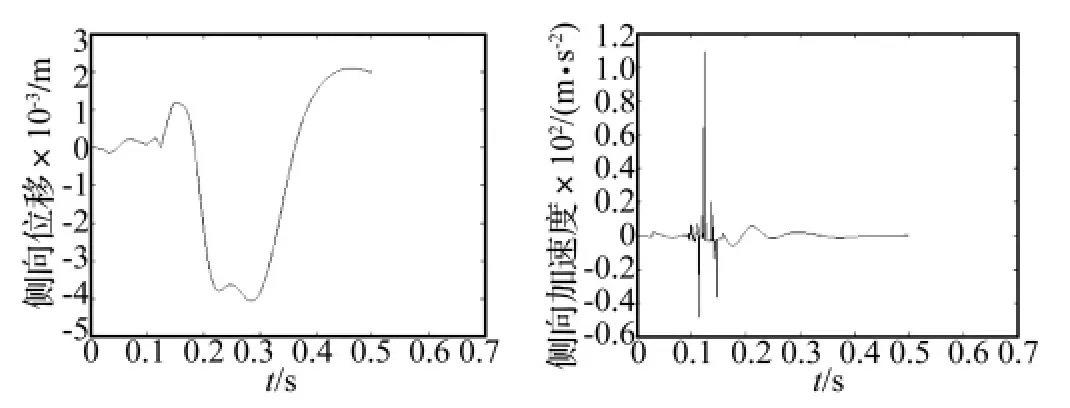
图3 发射过程中定向器前箍处的侧向的位移、加速度时间历程Fig.3 Time history of displacement and acceleration in horizontal direction at launch guider muzzle
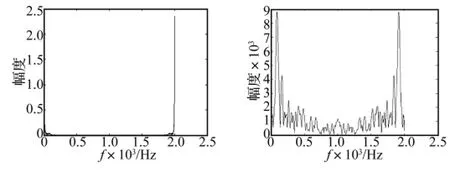
图4 发射过程中定向器前箍处的垂向的位移、加速度频谱特性Fig.4 The frequency characteristic of displacement and acceleration in vertical direction at launch guider muzzle
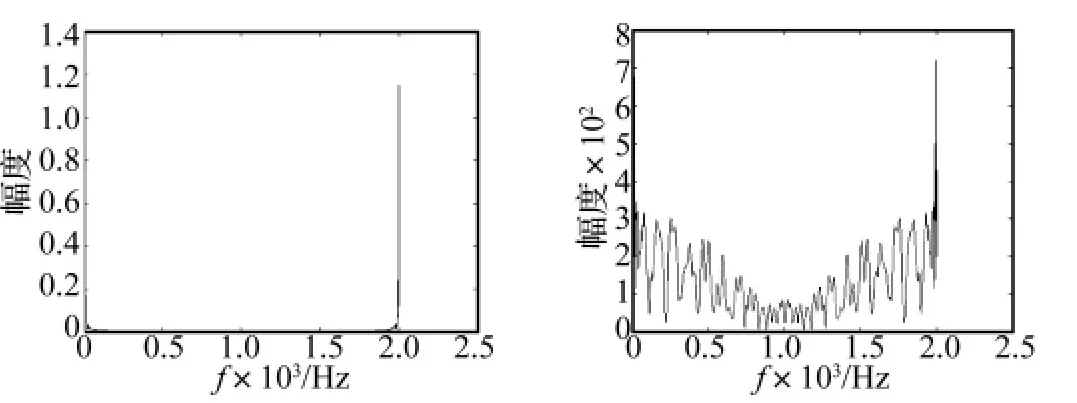
图5 发射过程中定向器前箍处的侧向的位移、加速度频谱特性Fig.5 The frequency characteristic of displacement and acceleration in horizontal direction at launch guider muzzle
4 定向器时频特性在数字滤波中的应用研究
4.1 Elliptic型数字滤波器特点和设计指标
数字滤波器通过对抽样数据或采集数据进行数学运算来达到频域滤波的目的,经典滤波器分为无限冲激响应(IIR)和有限冲激响应(FIR)滤波器[10],IIR滤波器主要是借助较成熟的模拟滤波器技术来实现,且滤波器阶数相对FIR滤波器较低,本文根据定向器的加速度信号频谱分析,利用Elliptic型的特点设计了IIR滤波器,并对试验中的定向器振动信号进行滤波采集。Elliptic型滤波器最大特点是将指标的精度均匀地分布在通带和阻带内,对于给定的结束和给定的波纹要求,除椭圆滤波器外,其他滤波器均不能获得较窄的过渡带宽。它的幅度特性是由雅克比椭圆函数决定的。幅度平方函数为:
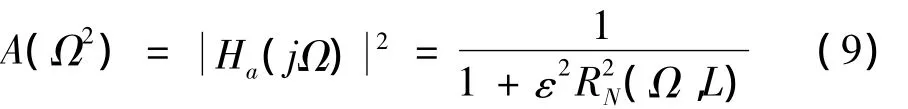
根据第3节的研究方法和内容可得到不同发射过程中定向器运动加速度信号的频谱范围,对定向器前箍处加速度信号滤波器提出设计要求为:采样频率为fs=2 kHz,通带边界频率fc=450 Hz,阻带边界频率fr=550 Hz,对应的数字角频率为ωc=2πfc/fs=1.413 7,ωr=2πfr/fs=1.727 9,通带波动Rp=1 dB,阻带衰减Rs=60 dB。根据以上设计要求,程序实现采用MATLAB编写,设计好的Elliptic滤波器的幅频特性如图6所示。
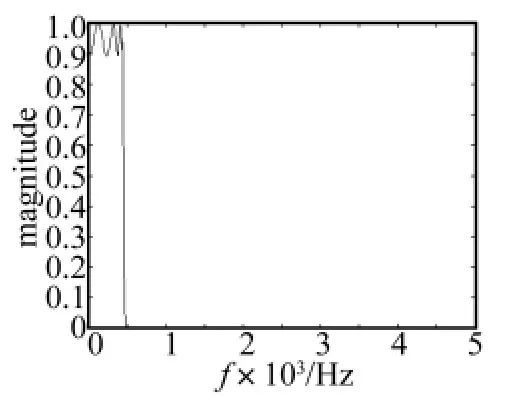
图6 Elliptic滤波器幅频特性Fig.6 The characteristic of the elliptic filter
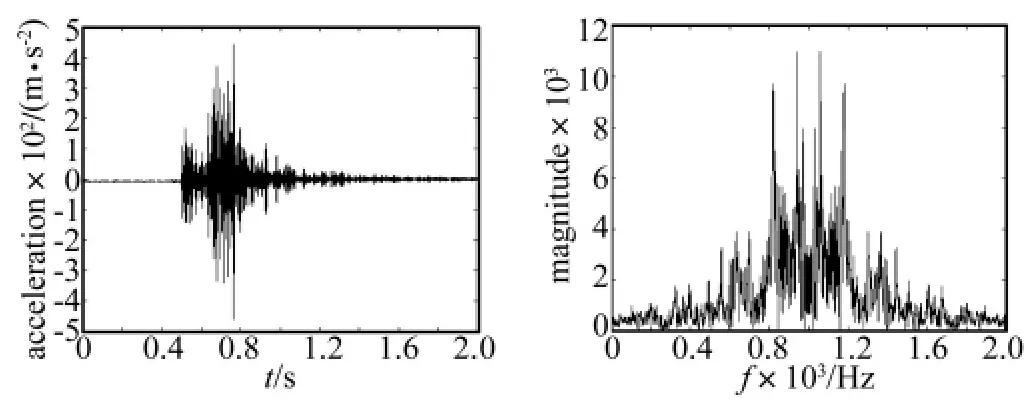
图7 试验中定向器前箍处的垂向的加速度时域历程和频域特性Fig.7 Time history of acceleration in vertical direction and frequency characteristic at launch guider muzzle in the test
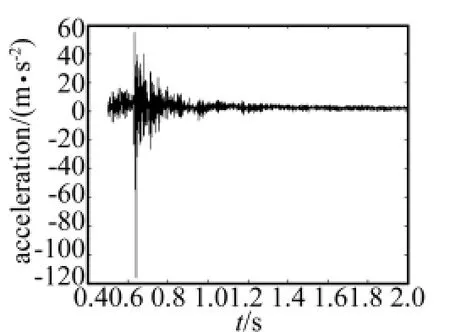
图8 垂向的加速度滤波结果Fig.8 The result of acceleration disposed in vertical direction
4.2 发射过程中多管火箭定向器加速度信号采集结果对比分析
在某次多管火箭泥土地发射试验中,把加速度计安装在定向器前箍处,对该点的垂向和侧向的加速度信号同时采集,图7是没有采用任何滤波时得到的多管火箭定向器前箍处在单发射击试验时获得的加速度信号的时域和频域曲线,其前0.5 s的时间为触发时间,图8是利用所设计的滤波器进行滤波采集的信号时间历程。从信号的幅度和振动收敛趋势的对比可见,经所设计的Elliptic滤波器处理的信号,大量高频噪声得到了有效的抑制,信号的幅值和振动衰减更趋于实际,达到了一定的滤波目的,但由于发射环境的复杂性,混频噪声的干扰依然比较明显,在发射过程中,如何更加准确地获取定向器振动信号是研究的另一个重要课题。
5 结论
本文基于实际工程需要为研究背景,利用多体系统传递矩阵法建立刚弹耦合的多管火箭发射动力学模型和仿真系统,通过多管火箭模态试验验证了系统的正确性;仿真得到发射过程中定向器束前箍处垂向和侧向的位移、速度和加速度等信号变化信息,利用信号离散傅里叶变换技术对信号进行频谱分析,获得了定向器发射过程中的定向器束前箍处垂向和侧向的位移、速度和加速度等信号的频谱特性;最后在研究基础上设计Elliptic滤波器,对定向器前箍处侧向和垂向加速度信号进行试验信号采集和滤波对比分析,验证了本文研究成果的正确性和重要性。发射过程中多管火箭定向器振动信号的时域和频域特性研究,为多管火箭发射过程中定向器振动信号的准确获取和振动的有效控制提供了重要的参考价值。
[1]Jitp raphai T,Burchett B,Costello M.A comparison of different guidance schemes for a direct fire rocket with a pulse jet control mechanism[R].AD20020513068,2002 -04.
[2] Cochran J E.Launcher/rocket system dynamics and passive control[C]. AlAA Atmospheric Flight Mechanics Conference.Albuquerque,New Mexico,USA:A IAA,1981:1-12.
[3]Hansen C H.Investigation of passive control devices for potential application to a launch vehicle structure to reduce the interior noise levels during launch[R].AOARD -99 -10,Australia,2000-11-04.
[4]潘宏侠.赵 剡.陈国光,等.振动对火箭炮密集度影响研究[J].兵工学报,2005(10):17-22.
[5]骆连珍,曹 勇.发射装置振动对火箭弹初始扰动的影响[J].弹箭与制导学报 X,1998(3):27-30.
[6]潘 硕.发射装置发射扰动测量与分析[D].南京:南京理工大学,2007:50-55.
[7]杨富峰,芮筱亭,展志焕,多管火箭起始扰动控制研究[J].南京理工大学学报,2010,34(1):63 -66.
[8]芮筱亭,贠来峰,陆毓琪,等.多体系统传递矩阵法及其应用[M].北京:科学出版社,2008:458-465.
[9]芮筱亭,陆毓琪,王国平,等.多管火箭发射动力学仿真与试验测试方法[M].北京:国防工业出版社,2003:106-198.
[10]吴镇扬.数字信号处理[M].北京:高等教育出版社,2004:55-69.

