半主动干摩擦阻尼器在隔振系统中的抗冲击优化设计研究
唐斯密,朱石坚,楼京俊
(海军工程大学 船舶与动力学院,武汉 430033)
在新形势下舰艇生命力已成为舰艇的重要指标,而舰艇抗冲击性能是舰艇生命力的重要组成部分,提高舰艇的抗冲击能力具有重要意义[1-2]。
传统的设计方法总是先进行隔振设计,然后进行抗冲击校核。通常隔振器刚度较小而具有较好的冲击隔离率,但是会产生较大的相对位移,工程上通常使用限位器来限制其相对位移,由于刚度突变,该措施又会恶化冲击隔离率[3]。所以,简单的依靠隔振器和限位器组成的抗冲系统并不具备优秀的抗冲性能,对隔振系统进行抗冲击优化设计具有重要的意义。
Sevin和Pilkey[4]针对冲击隔离的特点,提出了抗冲器在冲击隔离过程中的最优控制力,其模型以及变量的时间历程如图1所示:
设被隔离设备的质量为m,其最大加速度由控制力u(x)决定,如果抗冲器产生一个恒定的控制力u(如图1(b)所示),被隔离物体的绝对加速度将保持为a=u/m,如果被隔离物体可以承受的最大加速度为A,当a=A+ε(ε<0,且是一个极小值),就可以在保障设备安全的前提下,最大限度的降低相对位移。

图1 最优抗冲系统以及变量时间历程Fig.1 The optimal shock isolation model and varibles
虽然该理论已提出了多年,但是显然无法利用被动抗冲装置达到最优抗冲的目的。而主动装置则需要能输出大位移和大功率的小体积作动器,目前的工程上广泛应用的电磁式和超磁滞伸缩作动器均不具备这些条件,所以主动最优抗冲设计也仅为理论可行。随着抗冲击的发展和研究深入,越来越多的人认识到阻尼抗冲击的重要性,如果能对阻尼力进行合理的调节,就有可能在冲击响应的过程中,将阻尼力和弹性力的合力控制为近似恒定值,成为最优抗冲系统。
已有多名学者对半主动控制的磁流变阻尼器的隔振抗冲击系统进行了研究,如地震防护[5-7]、飞机起落架抗冲[8]、汽车悬架和座椅缓冲[9-11]的设计,这些设计通常针对持续时间较长的冲击或主要限制相对位移幅值,而对于舰船设备这类遭受持续时间很短的冲击设计研究较少。哈尔滨工程大学的姚熊亮、田振东等人利用磁流变阻尼器对舰船设备进行了抗冲设计[12-13],取得了较好的抗冲击效果,但是并没有从最优抗冲力这一设计着手,而是在整个冲击响应的过程中都保持着磁流变的恒定阻尼力,阻尼器与钢丝绳隔振器产生的合力显然不是最优抗冲力,该系统还有待进一步提高改进。海军工程大学的单树军等人[14]用磁流变阻尼器成功的实现了加速度峰值的削平,但是在实验中也发现了磁流变出力对电流的饱和作用,这在一定程度上限制了磁流变阻尼器在大冲击载荷下的抗冲性能。所以设计能产生大阻尼力的阻尼器也是成功实现最优抗冲设计的关键。
本文基于电磁和摩擦理论,设计了一个半主动式的干摩擦阻尼器,利用电流控制电磁力,该电磁力施加在摩擦面上,通过控制电流调节摩擦力的大小。所设计的电磁式干摩擦阻尼器和隔振器相并联,在没有冲击作用时,输入电流为零,不影响隔振性能。当系统遭受冲击作用时,以产生最优抗冲力为目标对摩擦力进行控制,以保证良好的抗冲击性能。本文在隔振设计的基础上,进行了抗冲击优化设计研究。
1 电磁铁建模
图2 为电磁铁原理图[15-16],假定磁铁之间的气隙为δ,两个线圈的两端间距为X,当X≫δ时,漏磁较小,可以认为气隙间的磁场分布均匀,大小为H0,磁阻为 μ0,设铁芯横截面积为A,线圈缠绕部分长为D,通过上下铁芯的磁场强度为H1和H2,磁阻为μ1,每个铁芯上有N匝线圈,上下磁铁在电压V的作用下,通过电流为I。
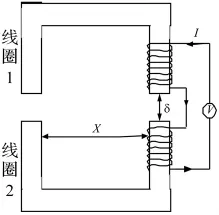
图2 电磁铁原理图Fig.2 The sketch of electromagnet
对图2做磁路分析:
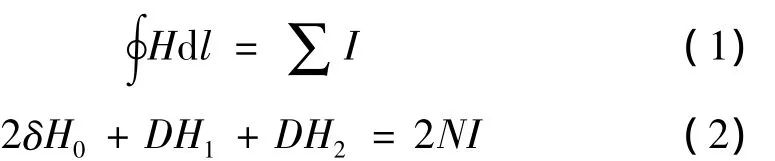
由H1=H2=B/μ1,H0=B/μ0,得到磁场强度B和铁芯中的磁通φ1、φ2:

其中φ1为穿过线圈1的磁通,由两部分组成:φ11和φ21,分别为线圈1自己产生的和线圈2在线圈1中产生的磁通。同理:φ2=φ22+φ12。
两个磁铁的自、互感系数与磁通、电流有如下关系:

由于1、2是相同线圈,有M=Mij,L=Lij。自感、互感之和为:
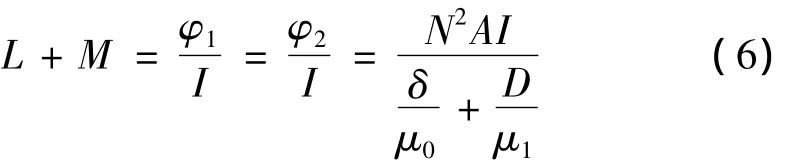
由此可以得到磁铁之间的总能量:

利用虚功原理,求得电磁力为:
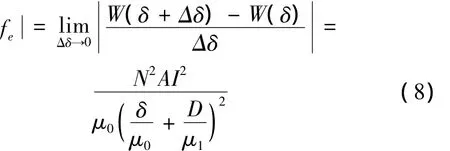
可以计算线圈1中的反电动势:

且e1=e2,可以推算出线圈1电压和电流以及反电动势的关系:

2 干摩擦阻尼器及抗冲击模型
2.1 干摩擦阻尼器模型
电磁式干摩擦阻尼器简图如图3所示,其主要组成部分为:1、导杆;2、摩擦片;3、电磁铁;4、套筒。

图3 电磁式干摩擦阻尼器简图Fig.3 The sketch of electromagnectic dry friction damper
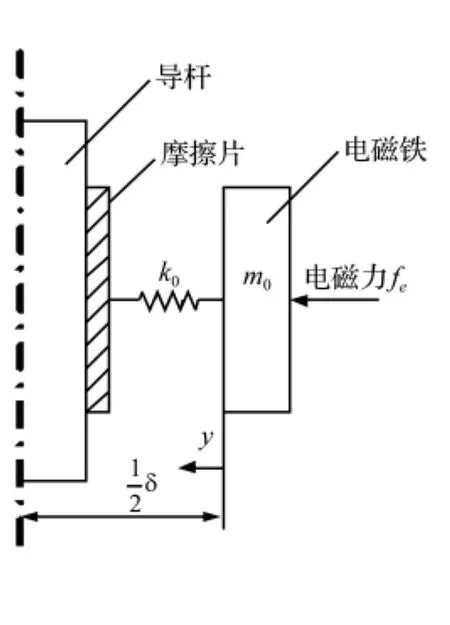
图4 干摩擦阻尼器动力学模型Fig.4 The dynamics model of dry friction damper
1的上端固定在被隔离设备的底部,随被隔离设备一起运动。2的内侧贴在1的外侧上,由1与2的相对运动产生摩擦力,其大小由3的电磁力决定。4的底部与基础相连接,2、3和4轴向保持固定,随基础一同运动。
导杆、摩擦片及电磁铁的动力学模型如图4所示,由于对称结构,以其中一侧进行分析:
设每块铁芯及缠绕线圈的质量和为m0,摩擦片为非刚性材料,其弹性系数为k0,电磁力fe作用在铁芯上,铁芯位移以y表示,导杆与摩擦片接触面上的力为f=k0y。电磁铁无电流通过时,电磁铁的初始间隙为δ0,当电磁铁作动时,该系统的动力学方程为:


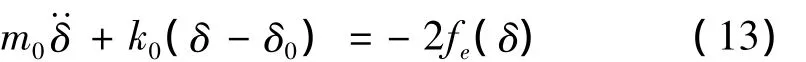
其中 δ∈(0,δ0]。
2.2 干摩擦力与抗冲击模型
摩擦力F与相对运动有关,当基础与被隔离设备有相对运动时,摩擦力的大小由电磁力和摩擦表面的情况决定,其方向总是与相对运动反向。当相对运动静止时,隔振器中的阻尼力为零,摩擦力与隔振器的弹性力方向相反。设最大静摩擦力为F0,摩擦力的表达式可以写为:
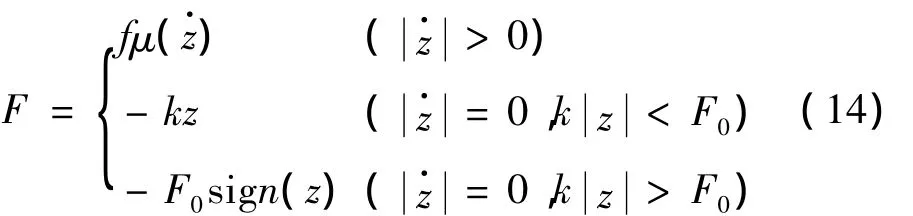
其中z和分别为被隔离设备与基础的相对位移和相对速度,f为施加在摩擦面上的力,μ()为导杆与摩擦片的摩擦系数,其大小与有关:在低速运动时,滑动摩擦系数随速度的增加而缓慢减小;但当速度增大到一定程度,由于摩擦表面发生粘着作用,产生的热量来不及散发,温度升高,导致摩擦系数急剧增加。其表达式可以写成[17]:

建立如图5所示的半主动干摩擦阻尼隔振抗冲击模型,被隔离设备和基础的位移分别用x和u表示。被隔离设备的质量为m,隔振器的线性刚度为k,阻尼为c。其中k和c为隔振器参数,假定在该参数下系统具有良好的隔振效果,对该系统进行抗冲击优化设计:附加一可控的干摩擦阻尼器,在隔振状态时,电磁铁无电流通过,摩擦力为零,不影响隔振性能。在基础有冲击输入时,调节控制电压,摩擦力大小为F。
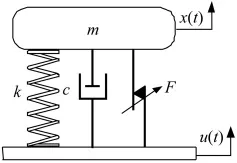
图5 半主动干摩擦冲击隔离模型Fig.5 Semi-active shock isolation model
建立冲击隔离的微分方程见式(16):

以相对位移z=x-u为广义坐标,基础的半正弦加速度(t)为冲击输入,冲击隔离方程为式(17):
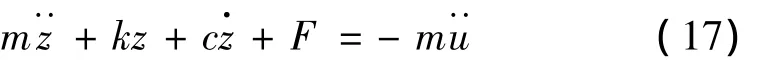
其中冲击输入:

U为基础加速度幅值,tm为冲击持续时间。
3 控制系统设计
如果能有效的控制摩擦力,使得其与隔振器的抗力之和为一个近似的恒定力,就可以大大的提高系统的抗冲击性能。目前控制方法已有很多,本文采用的是基于用传感器实时检测系统输出信号,经PID控制器对此信号进行动态调节,然后输出指令控制电压,继而改变摩擦力。半主动冲击隔离系统原理如图6所示。
虽然控制目标为作用力,考虑到力与加速度的关系,以及加速度传感器在工程上普遍使用,分别在基础和设备上各布置一个加速度传感器,系统作动的具体步骤如下:

图6 半主动冲击隔离系统原理图Fig.6 The sketch of semi-active shock isolation
(1)首先在目标信号中设定一个加速度值,该值略低于被隔离设备的最大可承受加速度。
(2)在基础与被隔离设备上各有一个加速度传感器,在没有受到冲击时,为保证隔振效果,电压源断开,干摩擦力为零。
(3)上下层传感器之差的积分为相对速度,当其超过某一阈值,认为此时冲击开始,控制器开始工作,调节电压输出,继而控制干摩擦力。
(4)上层加速度传感器将设备的实际加速度与目标信号相比较后,传递给控制器调整电压,使得设备的加速度保持在设定值附近。
(5)当相对速度小于某个阈值时,关闭控制器,在整个冲击响应阶段,由于阻尼作用,相对位移快速衰减。
(6)振幅衰减完成后,恢复隔振状态,等待下一次冲击开始。
4 数值模拟
假设被隔离设备的质量为m=100 kg,其可承受的最大加速度为25 g,系统允许的最大相对位移为20 mm,分别对该系统进行传统的抗冲击设计和半主动控制的优化抗冲设计,并加以比较:
(1)用隔振器抗冲击
选择隔振器的刚度为k=4×105N/m,其固有频率为10 Hz,阻尼系数为0.05,隔振器参数符合大多机电设备的隔振设计。
(2)用隔振器和限位器的组合抗冲击
选择限位器的刚度为2.4×106N/m,工作间隙为5 mm,对称安装在被隔离设备的上、下方。
(3)采用半主动干摩擦阻尼器抗冲击。
每个电磁铁质量m0=1 kg,线圈数为N=600匝,工作面积为A=10 cm2,初始间隙为δ0=2 mm,摩擦片的弹性系数k0=5×107N/m,与导杆的摩擦系数μ=2,非线性系数k1= -0.1 s/m,k2=0.005 s3/m3。PID 控制器的三个参数分别为:kp=5,ki=0和kd=0,相对速度超过0.5 m/s时即实施控制,目标是将设备的冲击响应加速度限制为23 g。
4.1 冲击响应比较
冲击载荷为基础的半正弦加速度冲击,冲击峰值为200 g,冲击持续时间为2 ms。使用数值方法计算系统的冲击响应。数值模拟的结果见图7。
在设定的冲击载荷下,隔振器虽然具有较高的冲击隔离率,加速度峰值仅为15 g,但是相对位移却达到了38 mm,远远超过了系统承受的极限,会对隔振器本身以及设备的连接管线造成破坏。隔振器和限位器的组合虽然将相对位移限制在了18.5 mm(极限值20 mm以下),但是设备的加速度峰值达到了41 g,远超设备可承受的极限,会对设备本身造成严重的破坏,此时隔振器或是隔振器和限位器的组合均不能满足抗冲击要求。使用干摩擦阻尼器的抗冲系统,加速度和相对位移分别为23 g和17.5 mm,均在允许的范围内。
4.2 极限性能比较
由于冲击时间通常很短,所以在抗冲设计时也通常用冲击速度V0作为冲击输入。设备冲击响应过程中,最大加速度J1与最大相对位移J2的乘积与冲击速度的平方之比,称为极限性能,三个变量之间具有如下关系:

式(19)称为极限性能公式,其值不可能小于0.5,值越接近0.5,表示抗冲击性能越好。
当冲击速度从2 m/s~3.5 m/s进行冲击时,分别对4.1节中的三个抗冲系统进行极限性能数值计算,结果如图8所示。
由极限性能的数值计算结果可以看出,有限位器的抗冲系统极限性能最差,虽然限位器能较好的限制相对位移,但代价是加倍放大被隔离设备的加速度。半主动抗冲器具有较好的极限性能,相对于隔振器和附加限位器的抗冲系统,能更好的调节加速度与相对位移的矛盾。
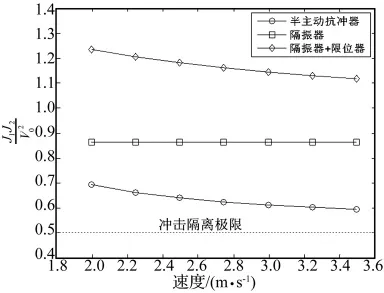
图8 极限性能比较Fig.8 Comparison of limiting performance analysis
通过4.1节~4.2节的算例可以看出,无论是冲击响应还是极限性能分析,隔振器虽然有良好的冲击隔离率,却无法限制相对位移。限位器由于存在刚度突变,往往造成加速度的放大,极限性能比隔振器更差。而通过最优抗冲设计,可以在限制加速度的同时,很大程度的降低相对位移。在传统抗冲设计严重失效的情况下,本文设计的半主动抗冲系统显示了良好的抗冲击性能。
5 结论
在舰艇生命力指标中,隔振和抗冲击都是其重要组成部分,但是传统的设计总是在隔振设计之后,作抗冲击校核或是简单的抗冲设计,如何在隔振设计的基础上,对其进行最优抗冲设计具有重要意义。本文基于最优抗冲力理论,设计了隔振器和半主动控制干摩擦阻尼器的隔振抗冲击系统。通过数值模拟可以看出,隔振器虽然具有较好的冲击隔离率,却往往伴随着较大的相对位移,隔振系统增加了限位器之后,虽然有效地限制了相对位移,却恶化了冲击隔离率,而半主动最优抗冲设计可以在保证设备安全的前提下,很大程度的降低系统的相对位移。该方法对于舰船隔振系统的抗冲击设计具有较好的指导意义。
[1]汪 玉,华宏星.舰船现代冲击理论及应用[M].北京:科学出版社,2005:1 -68.
[2] Rudolph J S,Henry C P.Naval shock analysis and design[M].The shock and vibration information analysis center booz,Allen and Hamilton,inc.USA,2000.
[3]赵应龙,何 琳,黄映云,等.限位器对隔振系统抗冲击性能的影响[J].振动与冲击,2005,24(2):71-76.
[4]Sevin E,Pilkey W D.Optimum shock and vibration isolation[M].Shock and Vibration Information Analysis Center,Washington,D.C.1971.
[5]Mcmanus S J,Clair K A S T.Evaluation of vibration and shock attenuation performance of a suspension seat with a semi-active maghetorheological fluid damper[J].Journal of Sound and Vibration,2002,253(1):313-327.
[6]徐龙河,周 云,李献忠.半主动磁流变阻尼控制方法的比较与分析[J].世界地震工程,2000,16(3):95-100.
[7] Laura M J,Shirley J D.Semiactive control strategies for MR Dampers:comparative study[J].Journal of Engineering Mechanics.2000,8:795-803.
[8] Mikulowski G,Holnicki-Szulc J.Adaptive aircraft shock absorbers[C],AMAS Workshop Materticals and Structures.2003,(3):63 -72.
[9]Jason E L,Glen A D,Wereley N M.Design of a magnetorheological automotive shock absorber [J].Proceedings of SPIE.2000,3985:424-437.
[10] Sapinski B,Rosol M.Real-time controllers for MR seat damper[J].Smart Materials and Structures.2003,3:181 -194.
[11]Mehdi A,James A N.Rheological controllability of doubleended MR dampers subjuected to impact loading[J].Smart Structures and Materials,2004,5386:185 -194.
[12]田正东,姚熊亮,沈志华,等.基于MR的船用减振抗冲隔离器力学特性研究[J].哈尔滨工程大学学报,2008,29(8):784-789.
[13]姚熊亮,邓忠超,张 明.船用智能抗冲击隔离器动力学数值试验分析[J].哈尔滨工程大学学报,2007,28(2):128-132.
[14]单树军,何 琳.可控阻尼半主动冲击隔离技术研究[J].振动与冲击,2006,25(5):144 -147.
[15]冯慈璋,马西奎.工程电磁场导论[M].北京:高等教育出版社,2000.
[16]白志红,周玉虎.电磁铁的动态特性的仿真与分析[J].电力学报,2004,19(3):200 -204.
[17] Thamsen JJ, Fidlin A. Analyticalapproximationsfor stickslip vibration amplitudes[J].Intenational Journal of Non-Linear Mechanics,2003,38:389 -403.

