基于COMSOL的声表面波器件仿真*

阮 鹏,陈智军,2,付大丰,张亦居,王萌阳

(1.南京航空航天大学自动化学院,江苏南京 210016; 2.南京大学近代声学教育部重点实验室,江苏南京 210093)

声表面波(Surface Acoustic Wave,SAW)是一种沿固体表面传播的弹性波,能量集中在固体表面1～ 2个波长的范围内[1],可利用沉积在压电基片表面的叉指换能器(Inter-digital Transducer,IDT)来有效激发[2].SAW器件在通信、传感、射频识别等领域都有着极为广泛的应用,最常见的结构为“半无限压电基片-叉指换能器”形式[3-4].随着研究的不断深入,出现了各种改进的SAW器件结构,譬如在叉指换能器表面溅射一层薄膜的乐甫波(Love Wave)器件[5].由于适合液体检测,乐甫波器件成为声表面波器件的研究热点[6-7].

在对声表面波器件的研究过程中,器件仿真工作是器件设计和制作的基础,通过仿真可以提高设计效率、减少制造过程中的材料浪费等.声表面波器件的仿真可基于脉冲响应模型、等效电路模型、耦合模型等方法,通过编写代码进行数值分析[8].随着ANSYS、ANSOFT、COMSOL等大型有限元分析软件的出现,可利用上述软件对SAW器件进行仿真分析,从而省去人工编写代码的繁琐流程[9].

与ANSYS、ANSOFT等有限元仿真软件相比,COMSOL具有以下显著特点:①完全开放的架构,用户可以自由定义所需专业的偏微分方程;②专业的计算模型库,内置各种常用的物理模型,用户可以选择参考并进行必要的修改;③丰富的后处理功能,可根据用户需要进行各种数据、曲线、图片及动画的输出与分析[10].

本文基于COMSOL建立了SAW器件的有限元分析模型,得到了直观的SAW传播形式;仿真分析了SAW器件的频率特性,探讨了IDT在不同敷金比、高度比时的SAW器件频率变化.在此基础上,研究了在IDT表面溅射一层薄膜时的乐甫波器件频率特性;当薄膜上负载液体时,通过器件频率对液体密度的灵敏程度来对薄膜厚度进行了优化.其研究结果可以为声表面波器件的精确设计提供仿真依据.

1 模型的建立

声表面波器件是一种典型的谐振式器件,特征频率是器件的主要参数[11-12].当声表面波器件用做传感器时,主要通过特征频率随待测量的变化来实现检测功能.在有限元分析中,模态是机械结构的固有振动特性,每一个模态具有特定的特征频率和模态振型.因此,通过有限元软件COMSOL的模态分析模块可仿真研究声表面波器件的频率特性.

图1 声表面波器件结构Fig.1 The structure of surface acoustic w ave device

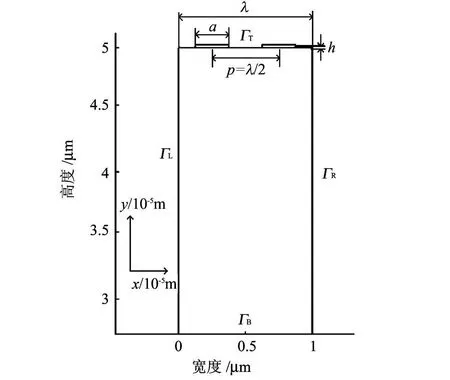
图2 模态分析二维模型Fig.2 2D model of analysis

声表面波器件的结构如图1所示.IDT沉积在压电基片表面,由周期性排列并与汇流条交替连接的多对电极构成.利用周期性边界条件,可把IDT简化为由一对电极组成的周期结构,从而建立简化的二维模型以减小计算量.声表面波器件的模态分析二维模型如图2所示.横、纵坐标的单位:μm,基片宽度与声表面波波长 λ一致;由于声表面波的能量主要集中在基片表面1～2个波长深度内,随着基片深度的增加其振幅呈指数衰减,因此基片高度可简化为2～5倍波长;电极中心间距p=λ/2.

模型边界条件的设定如下:

1)上表面边界条件 ΓT为自由边界条件;

2)下表面边界条件 ΓB为固定边界条件;

3)左右边界条件 ΓT、ΓR为一对周期性边界条件,即左右边界上对应节点的3个自由度(x方向位移u,y方向位移v,电势 Φ)相等.

二维模型各参数如表1所示.

表1 模态分析二维模型参数Tab.1 Param eter of 2D analysismodel

基片材料为压电陶瓷PZT-5H,其密度ρ为7 500 kg/m3,压电、弹性、介电常数分别为

IDT采用金属铝电极,其密度 ρIDT=2 700,kg/m3,杨氏模量E=70e9, Pa,泊松比v=0.33.

建立完备的几何模型还需要进行网格划分.网格划分越密,计算结果越精确,但是计算量会大大增加,因此合适的网格划分是求解的关键.COMSOL软件的网格划分可以分为初始化网格、细化网格和自由网格三种方法.初始化网格由软件根据几何模型粗略进行自动网格划分,根据模型各处结构的复杂程度决定网格尺寸;细化网格在初始化网格的基础上由软件进行更密集的划分;自由网格对用户开放,用户可以设定最大单元尺寸、单元增长率等参数,并可以决定局部细化的区域.

网格划分后的二维模型如图 3所示.首先对整体模型结构进行初始化网格,但由于声表面波集中在基片表面1～2个波长内传播,因此再对基片表面进行局部细化.

图3 模型的网格划分Fig.3 Meshing of model

2 无电极压电基片结构

在实际应用中,通常通过IDT来有效激发出声表面波.如果不考虑声表面波激发原理,仅考虑其传播时需要满足的边界条件,同样可以通过COMSOL的模态分析模块来研究无电极压电基片结构的声表面波特征频率,此时只需在上述模型中去掉叉指电极即可.

在模型建立完成后,选择特征频率处理器,确定求解范围来进行声表面波特征频率的分析.利用声表面波能量集中在基片表面1～2个波长深度内的特点,可以把声表面波振型从很多各不相同的波动振型中提取出来,得到特征频率.

声波振型如图4所示,图中右边的颜色刻度表示振动位移大小,颜色从上到下表示振动位移减弱.根据振动位移随基片深度的变化趋势,图4(a)为体波振型,图4(b)为声表面波振型,其对应的声表面波特征频率f为189.78MH z.通过多次仿真表明,每一个无电极压电基片模型对应唯一的声表面波振型.

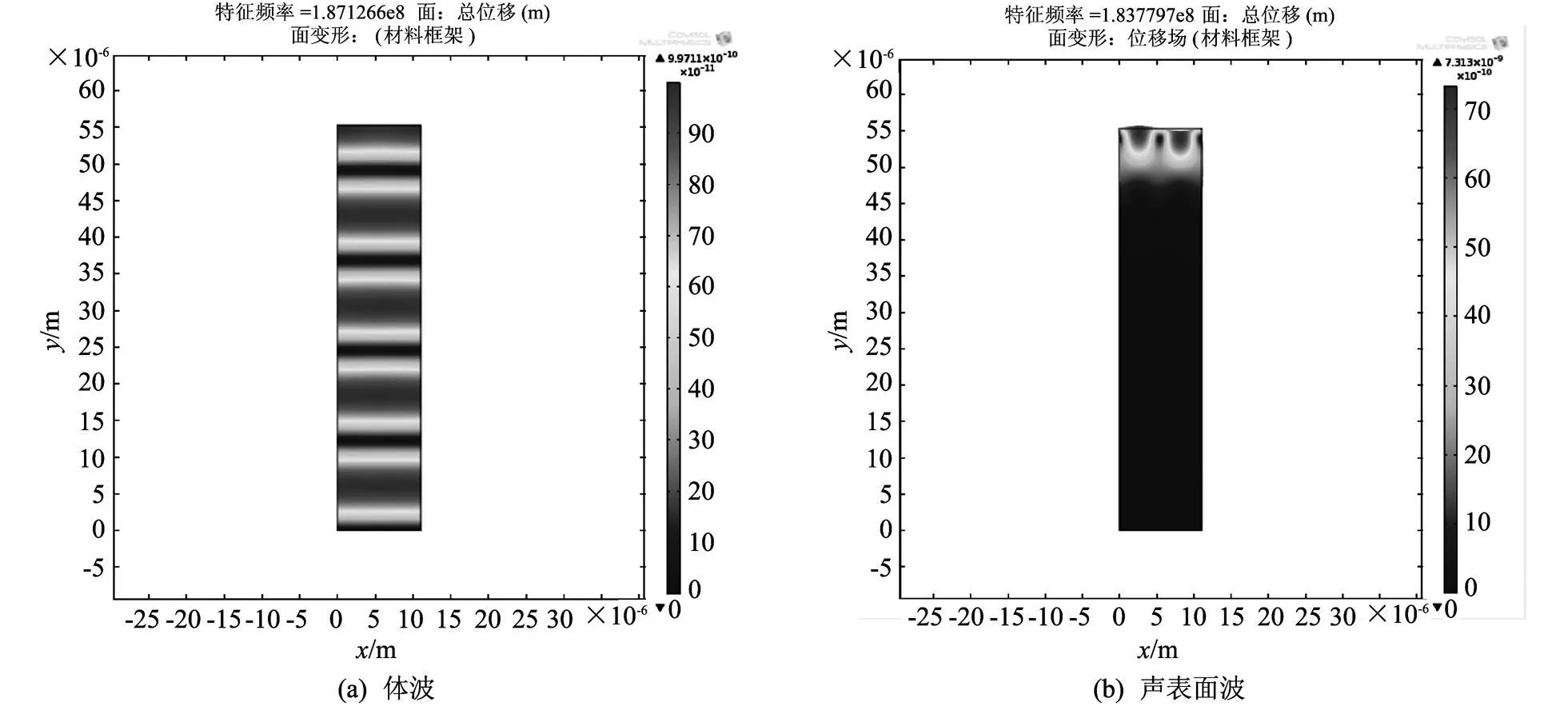
图4 声波振型Fig.4 Acoustic w ave vibration model

3 压电基片-叉指换能器结构

3.1 叉指电极敷金比分析

当压电基片上沉积叉指电极时,以表 1所述的模型参数进行仿真.与无电极压电基片结构不同的是,通过模态分析模块可以提取到两个符合声表面波振型的特征频率,定义为正特征频率fsc+和反特征频率fsc-分别如图5(a)、(b)所示.

表2 声表面波特征频率随MR的变化Tab.2 Resonant frequencies of Surface acoustic w ave's change with MR

正特征频率和反特征频率的出现是由于 IDT的电极效应引起[13].定义叉指电极敷金比MR=a/P,当=0时,可以等效为基片上表面无电极情况,为自由化边界条件,此时表面电荷密度 σ =0;当MR=1时,可以等效为基片上表面覆盖一层金属薄膜,为金属化边界条件,此时表面电势Φ=0.通过仿真分析,得到正、反特征频率随的变化如表2所示.

当0＜MR＜1,随着MR的增大,正、反特征频率逐渐减小.当MR=0与MR=1时,基片上表面分别处于自由化边界条件和金属化边界条件,不存在IDT的电极效应,正特征频率和反特征频率退化为一个特征频率.

3.2 叉指电极高度分析

在敷金比分析的基础上,取=0.5时进行IDT高度的分析,即在IDT宽度不变的前提下,研究IDT电极高度对拓征频率的影响.定义叉指电极高度比

特征频率随叉指电极高度比Q的变化如表3所示.

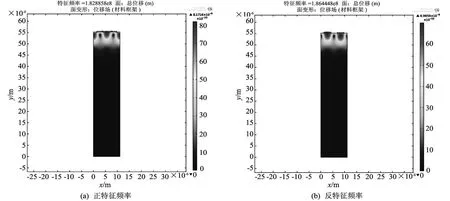
图5 正、反特征频率振型Fig.5 The vibration m odel of resonan t and an ti-resonan t frequency

表3 特征频率随叉指电极高度比 Q的变化Tab.3 Resonant frequen cies'change w ith the heigh t of IDT

由上述分析可知,Q=0时,正、反特征频率相等,其原因在于Q=0与=0等效,相当于无电极压电基片结构.其它情况下叉指电极均激发出正、反特征频率,并且当Q值增大时,正、返特征频率会向低频偏移.

4 压电基片-叉指换能器-薄膜结构

在“压电基片-IDT”结构的基础上,在IDT表面溅射一层薄膜时,该结构称为乐甫波器件.乐甫波器件是一种新型的声表面波器件,因适于液体检测而成为研究热点.

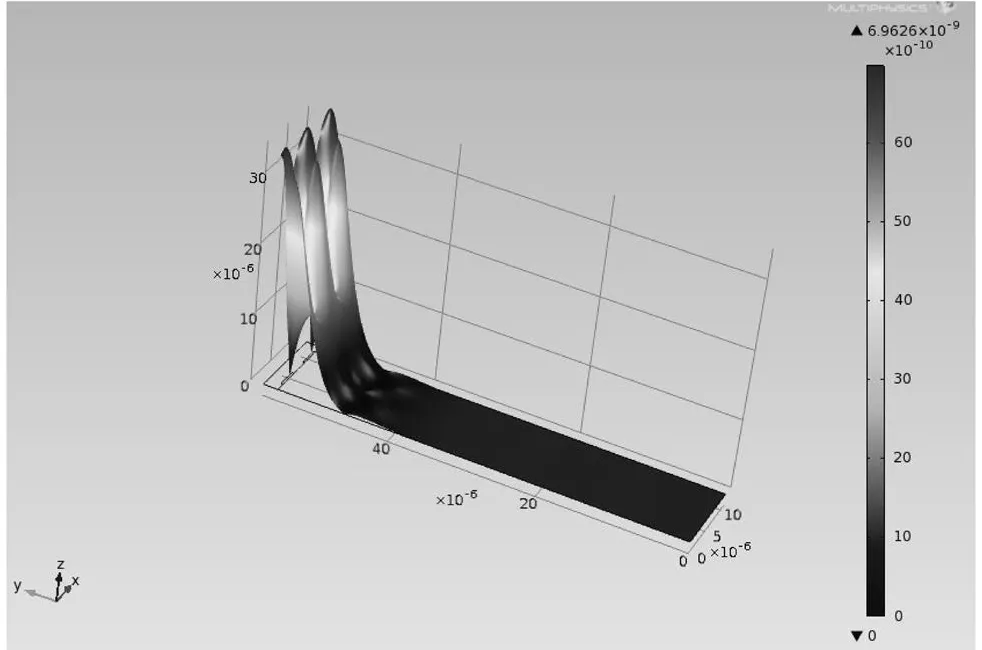
图6 乐甫波三维振型Fig.6 3D vibration m odel of love w ave

图7 乐甫波特征频率 f随薄膜厚度d的变化Fig.7 Resonant frequencies of love w ave's change w ith the thickness of th in film

器件模型在图2的基础上增加一层薄膜,薄膜材料选择二氧化钛(TiO2),薄膜上表面为自由边界条件,左右边界条件为一对周期性边界条件.乐甫波三维振型如图6所示.从图6可以看出,振动能量主要还是集中在压电基片表面一个波长深度左右,并且薄膜上的振动也很明显,这可以为液体的检测提供很好的保证.

乐甫波特征频率随薄膜厚度的变化,如图7所示.从图7可知,与IDT高度的影响相似,由于薄膜的质量加载效应,特征频率同样随薄膜厚度的增大有向低频偏移的趋势.

5 压电基片-叉指换能器-薄膜-液体结构

基于“压电基片-IDT-薄膜”结构,在薄膜上负载液体时,乐甫波三维振型如图8所示.由图8可知,振动位移不会产生压缩波进入液体,从而不会向液体介质辐射能量,因此乐甫波在传播过程中不会产生太大衰减,表明了乐甫波用于液体检测的优势.

当乐甫波器件用于液体密度检测时,定义灵敏度

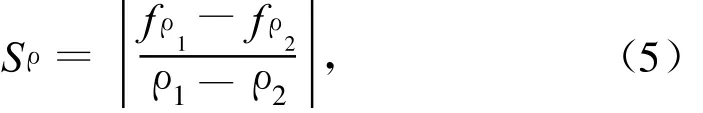
图8 负载液体的乐甫波三维振型Fig.8 Love wave 3D vibration m odel of load ing liquid

式中:ρ1和 ρ2为液体的密度;fρ1和fρ2分别为负载上述密度液体时对应的乐甫波特征频率.

灵敏度Sρ随薄膜厚度的变化,如图9所示.从图9可知,灵敏度Sρ首先随薄膜厚度d的增大而增大;当d=5μm,即d/λ≈0.45时,灵敏度Sρ达到最大;之后随d的增大而减小,并最终趋于稳定.

选择薄膜d最优厚度为5μm时,乐甫波特征频率f随液体密度的变化,如图10所示.从图10可知,乐甫波器件用于液体密度检测时具有较好的线性度.

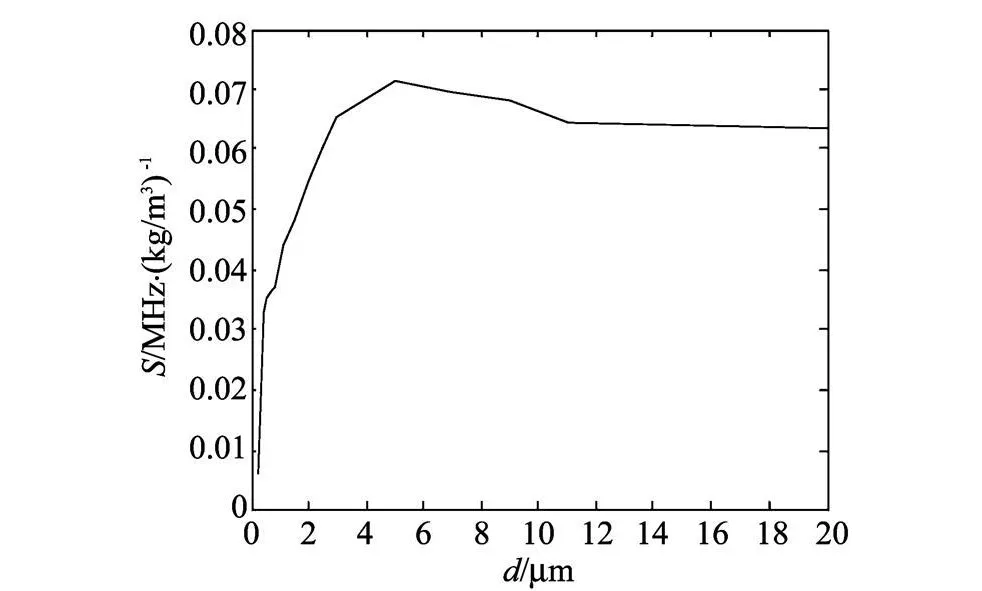
图9 灵敏度Sρ随薄膜厚度d的变化Fig.9 Sensitivities'change w ith the thickness of thin film

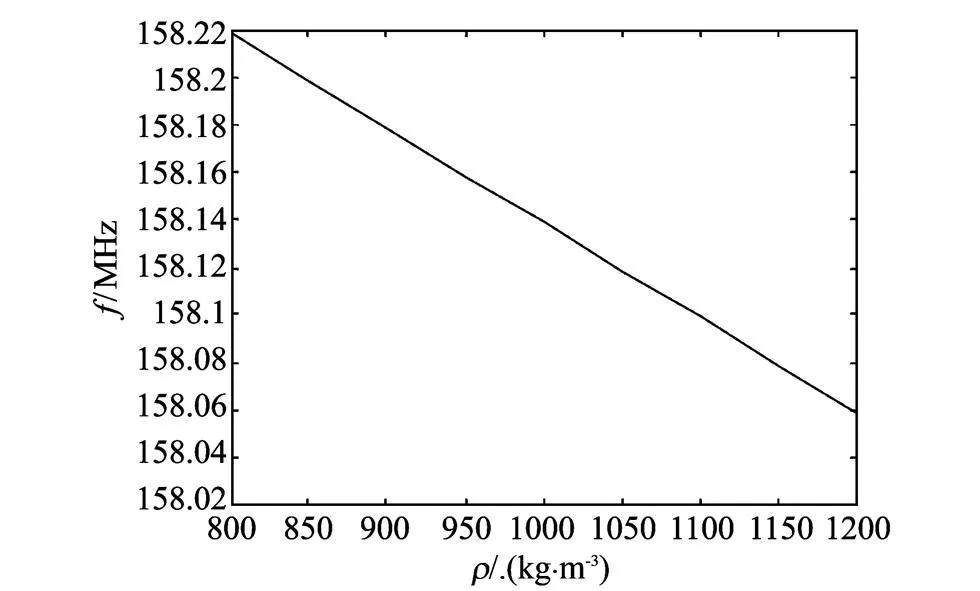
图10 乐甫波特征频率 f随液体密度的变化Fig.10 Resonant frequencies of love w ave's change w ith the density of liquid

6 结 论

利用有限元软件COMSOL,按由浅入深的顺序对无电极压电基片、压电基片表面沉积叉指换能器、叉指换能器表面溅射薄膜、薄膜上负载液体的4种声表面波器件结构进行了仿真分析,可得出以下结论:

1)通过有限元软件COMSOL的模态分析模块,利用声表面波能量集中在基片表面1～2个波长深度内的特点,可以把声表面波振型从很多各不相同的波动振型中提取出来,并得到特征频率.

2)对于无电极压电基片结构,每一个模型对应唯一的声表面波振型.

3)叉指换能器的电极效应会产生正、反特征频率,而且正、反特征频率随着叉指换能器敷金比与高度比的增加而向低频偏移.

4)对于“压电基片-叉指换能器-薄膜”结构,乐甫波振动能量主要还是集中在压电基片表面大约一个波长深度,并且薄膜上的振动也很明显.与此同时,由于薄膜的质量加载效应,特征频率随薄膜厚度的增大有向低频偏移的趋势.

5)在薄膜上负载液体时,振动位移不会产生压缩波进入液体,从而不会向液体介质辐射能量,因此乐甫波在传播过程中不会产生太大衰减,表明了乐甫波用于液体检测的优势.

6)当乐甫波器件用于液体密度检测时,可通过器件特征频率对液体密度的灵敏程度对薄膜厚度进行优化.仿真结果表明,乐甫波器件用于液体密度检测时具有较好的线性度.

[1] Morgan D P.History of SAWdevices[C].In Proceedings of IEEE International frequency control symposium,Piscataw ay, NJ,USA,1998:439-460.

[2] 水永安.声表面波与声表面波器件讲义[R].南京:南京大学电子科学与技术系,1998.

[3] Hashimoto K Y.Surface AcousticWave Devicesin Telecommunications:Modeling and Simulation[M].Berlin,Heidelberg: Springer-Verlag,2000.

[4] 陈明,范东远,李岁劳.声表面波传感器[M].西安:西北工业大学出版社,1997.

[5] Tamarin O.Study of acoustic Love wave devices for real timebacteriophage detection[J].Sensors and Actuators,2003,B (91):275-284.

[6] 胡友旺,史建亮,贾宏光,等.Love波传感器及其质量灵敏度测试[J].传感技术学报,2006,19(5):2126-2129.

Hu Youwang,Shi Jianliang,Jia Hongguang,etal.Lovew ave sensor and themeasurementofmass sensitivity[J].Chinese Journal o f Sensors and A ctuators,2006,19(5):2126-2129.(in Chinese)

[7] 江城,倪世宏,李红浪,等.Love波飞机结冰传感器研究[J].航空学报,2009,30(5):906-911.

Jiang Cheng,NiShihong,LiHonglang,etal.Study of lovew aveaircraft ice sensor[J].Acta Aeronautica et Astronautica Sinica,2009,30(5):906-911.(in Chinese)

[8] 吴佚卓.高频无线无源声表面波传感器的仿真与测试研究[D].天津:天津理工大学,2006.

[9] Peng Dasong,Yu Fengqi.A novelFEA simu lationmodel for RFIDSAWtag[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2009,56(8):1753-1760.

[10] K rishnan R N,Nemade H B,Paily R.Simulation ofOne-PortSAWResonator using COMSOLMultiphysics[C].Boston, Proceedings of the COMSOL Users Conference,2006.

[11] 戴恩光,冯冠平.对SAW谐振器气体传感器的表面质量负载与传感器性能之间关系的研究[J].测试技术学报, 1996,10(4):349-353.

Dai Enguang,Feng Guanping.The research in the relationships betw een the loading effects and the performance of sensor based upon SAWresonator[J].Journalof Test and Measurement Technology,1996,10(4):349-353.(in Chinese)

[12] Drafts B.A coustic wave technology sensors[J].IEEE Transactions on Microwave Theory and Techniques,2001,49(4): 795-802.

[13] 卢旭.基于COMSOL的声表面波标签仿真[D].南京:南京航空航天大学,2011.