乐甫波器件的幅频特性研究*

陈 涛,陈智军,2,阮 鹏,王萌阳,黄 鑫

(1.南京航空航天大学自动化学院,江苏南京 210016;2.南京大学近代声学教育部重点实验室,江苏南京 210093)

乐甫波是一种界面波,是在由半无限压电基片和各向同性非压电薄膜构成的层状结构中传播的声波,非压电薄膜作为波导层沉积或溅射在压电基片表面.乐甫波的质点振动沿水平剪切方向,不存在基片法线方向的振动.因此,乐甫波器件与液体接触时能量损失小,能够用于液体传感.乐甫波器件是一种新型声波器件,由于具有灵敏度高、响应速度快、体积小、适于液相检测等优点,从而成为当前声波传感领域的研究热点[1-2].声波器件用于传感时,主要通过声波谐振频率和幅度衰减随被测对象的变化来实现检测功能[3].无论采用相位差测量方法、振荡电路测量方法或是扫频测量方法,其本质都是基于乐甫波器件的幅频特性来搭建测试系统.因此,对乐甫波器件的幅频特性仿真有助于器件的设计、制作及测试系统搭建.与此同时,薄膜厚度是乐甫波器件的重要参数[4],需要重点研究薄膜厚度对器件幅频特性的影响以指导乐甫波器件的设计.

本文基于部分波理论和表面有效介电常数方法来计算乐甫波传播速度、谐振频率和机电耦合系数,在梅森等效电路中加入波导元件得到乐甫波器件的等效电路模型.使用Matlab对其数学模型进行了幅频特性分析,其仿真曲线与实际器件测试结果基本一致,并在此基础上研究了薄膜厚度变化对乐甫波器件幅频特性的影响,其研究结论可以为乐甫波器件的设计提供理论指导和仿真依据.

1 谐振频率模型

乐甫波器件如图1所示,用于激发乐甫波的叉指换能器(Inter-digital transducer,IDT)沉积在压电基片和薄膜之间,乐甫波只在水平剪切方向x2存在质点振动.乐甫波器件坐标系可简化为如图2所示的二维坐标系.+x1为声波传播方向,+x3为基片表面法线方向,薄膜的厚度为d.谐振频率的建模包括压电基片上的声场分量建立、薄膜上的声场分量建立、边界条件求解三个部分.

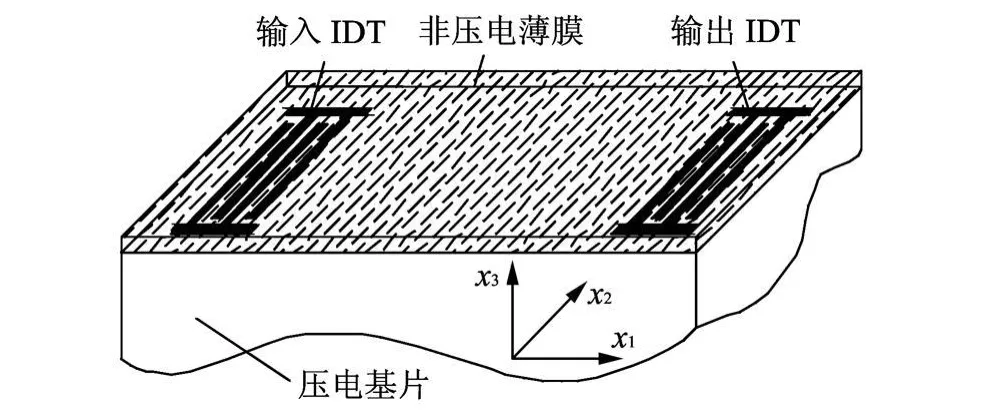
图1 乐甫波器件结构图Fig.1 Chart about Love w ave device

图2 乐甫波器件坐标系Fig.2 Coordinate system about Love wave device

在准静态近似下,采用Einstein求和约定的耦合波方程为[5]

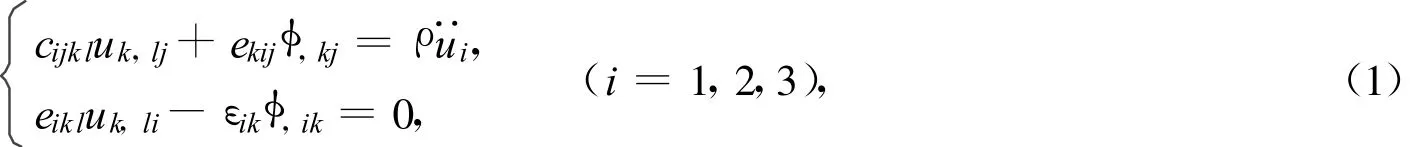
式中:cijkl,ekij,εik分别为压电介质的弹性常数、压电常数和介电常数;ρ为压电材料的密度;u,φ描述声振动的场量为机械位移和电势.

压电基片上IDT激发出的声波属于平面波,声场分量的表达式具有式(2)形式

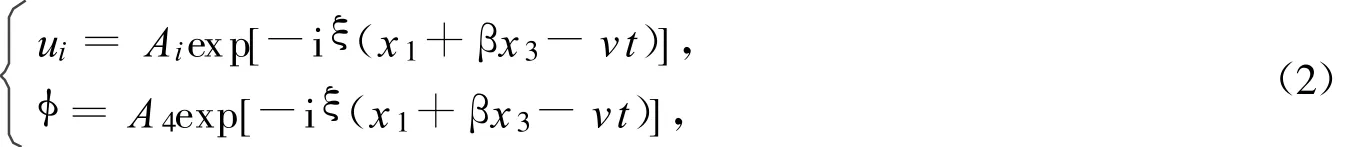
式中:Ai,A4分别为各位移分量和电势的振幅;v为乐甫波的传播速度;ξ为乐甫波沿传播方向的波矢; β表征声场沿x3方向的变化因子.

将式(2)代入式(1),得到Christoffel方程组.乐甫波由于只在水平剪切方向上存在振动,(u2,φ)与(u1,u3)解耦,Christoffel方程组会退化为两个独立的子方程组[6].其压电介质中的Christoffel方程组可写成矩阵形式

式中:A为矢量[];Г为与压电基片材料特性和β有关的一个2×2系数矩阵.

对传播速度v假定一个值,令式(3)中的系数行列式为零,可求得β的4个根.为保证乐甫波在半无限压电基片的界面上传播,选取为正的两个根 β(α)(α=1,2).将β(α)代入式(3),得到两个根各自对应的位移振幅和电势振幅.根据部分波理论[7],IDT激发出的乐甫波在压电基片上即为两个部分波的线性叠加

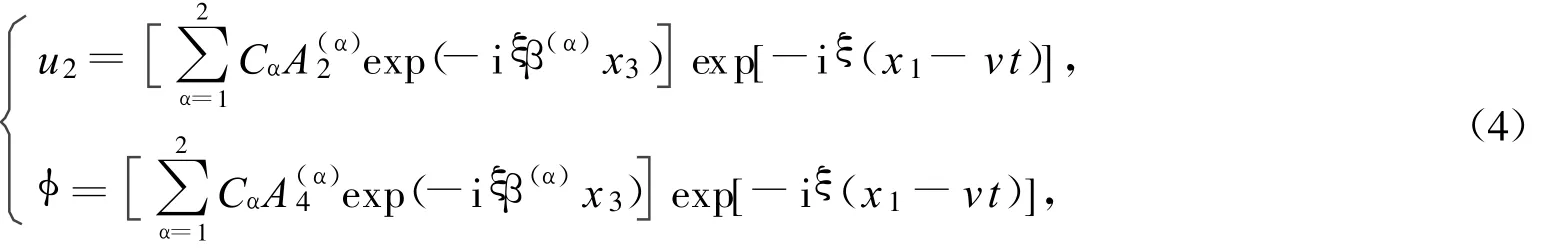
式中:Cα为压电基片中部分波的加权系数.

薄膜上声场分量的建立过程与压电基片类似,其不同之处在于薄膜属于各向同性非压电介质,(u1,u3)、u2与 φ分别解耦,其部分波理论需要分别应用于薄膜的位移(u1,u3)、u2和电势 φ.除此之外,与半无限压电基片相比,薄膜的厚度有限,因此,在根据薄膜的Christoffel方程组系数行列式为零来求得相应 β的过程中,不存在选取正根的环节[8].

除x3=0处的电学边界条件之外,乐甫波传播的边界条件可写成矩阵形式

式中:C为由压电基片及薄膜中的部分波加权系数构成的向量组;N为一个6×7矩阵.

式(5)实际上是一个包括6个方程的方程组,6个方程分别表征的意义如下:=0上的法向应力连续性条件,x3=0上的位移连续性条件,x3=0上的电势连续性条件,x3=d上的法向应力T32=0,x3=d上的电势连续性条件,=d上的电学边界条件.

界面x3=0处的电学边界条件有两种情况:当该界面为自由化时,界面自由电荷密度 σ为0;当该界面为金属化时,界面的电势 φ为0.为方便仿真,引入表面有效介电常数

图3 乐甫波的表面有效介电常数曲线Fig.3 The surface effective perm ittivity curve about Love wave

对于每一个假定的传播速度v,由式(5)可求得各部分波的加权系数之比,将其代入式(6)即可计算出 εeff.当x3=0界面为自由化时,εeff=0;当x3=0界面为金属化时,εeff=∞.因此,εeff的一组零极值对应着乐甫波实际的传播速度vf(自由化界面)和vm(金属化界面).以压电基片材料为36°YX钽酸锂,非压电薄膜材料为SU-8光刻胶为例,当薄膜厚度d与声波波长λ之比d/λ=0.025时,乐甫波的表面有效介电常数曲线如图3所示,根据该曲线可计算出vf和vm.

当叉指周期P与声波波长λ一致时,乐甫波器件处于谐振状态.乐甫波谐振频率为

机电耦合系数反映了压电基片的机械能和电能之间通过压电效应相互耦合的强弱,表征了声波的激发效率,其定义为

2 等效电路模型

声表面波器件的核心是IDT.根据交叉场理论,声表面波器件一个周期段的IDT可采用梅森(Mason)等效电路模型来等效[9].乐甫波器件一个周期段的IDT等效电路如图4所示.该电路在梅森等效电路的基础上加入了波导元件[10],同样具有两个声学端和一个电学端.图中,θ=2π(f/f0),为电极一个周期段的渡越角;R0为IDT的特性阻抗;Cs表示单对指电极的电容.

对于具有N个周期段的输入IDT,将其每个周期段等效电路模型的声端串联、电端并联,可得到整个输入IDT的等效电路模型,如图5所示.其等效电路同样为三端口网络,各端口之间的电流电压关系采用导纳矩阵 Y表征[11].

在谐振频率附近,导纳矩阵 Y为

图4 乐甫波器件一个周期段的IDT等效电路模型F ig.4 One period IDT's equivalent circuit model about Love w ave device

式中:G0=1/R0=/2,为特性导纳;δ =2π(f-f0)/f0,表示偏移谐振频率的量;CT=NCs,为IDT的总电容.

可进一步简化IDT的电端输入导纳为

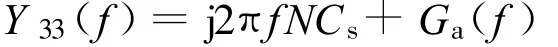
式中:Ga(f)是辐射导纳,x=Nπ(f-f0)/f0.

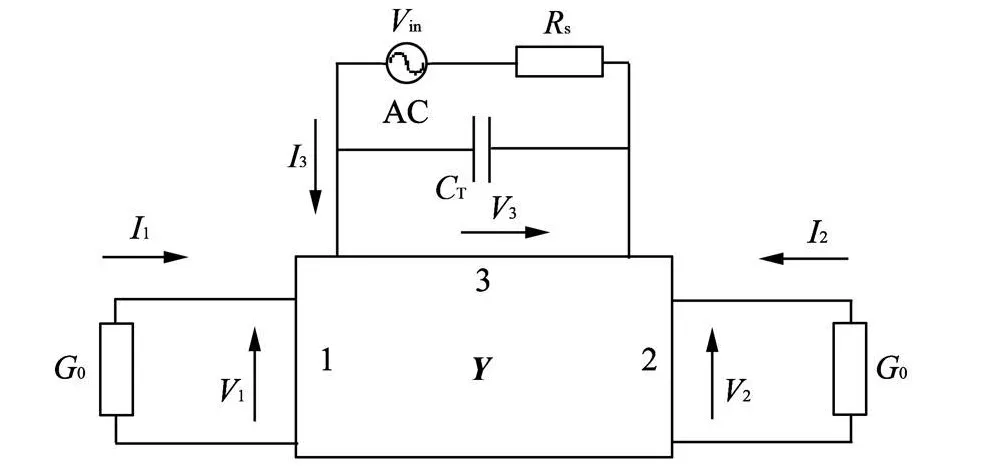
图5 乐甫波器件的输入IDT等效电路模型Fig.5 Input IDT's equivalen t circuit model about Love wave device

图6 输入-输出IDT的双端口等效电路模型Fig.6 Duam-por t equivalen t circuitm odel abou t input-output ID T

对于乐甫波器件,单对指电极的电容为[12]

式中:w为IDT孔径;a为叉指宽度;l为相邻叉指中心之间的距离

式中:ε1为薄膜介电常数;ε2为基片介电常数;d为薄膜厚度.

以上分析均将IDT视为三端口网络.在测量乐甫波器件时,只关心输入、输出IDT在电学端口3的电压比值,因此将总的输入-输出IDT网络视为双端口等效电路模型,如图6所示.在得到单个IDT的y参数后,可求出输入-输出IDT的总网络方程.

根据电路理论,由图6可得到输入-输出IDT的电流-电压关系

式中:L是输入-输出IDT的中心距.

输入信号电压Vin=Va+IaRs,其中Rs为信号源内阻;负载RL上的电压为VL=Vb.因此可求得输入-输出IDT的电压传输函数为

当信号源内阻Rs和负载电阻RL不相等时,插入损耗(Insertion Loss)定义为

将式(15)代入(16),可得

插入损耗IL是频率f的函数,由此可仿真出乐甫波的幅频特性曲线.根据上述乐甫波的等效电路模型推导过程可知,当薄膜厚度变化时,仿真得到的幅频特性曲线也会随之变化.

3 器件测试与数值仿真

通过网络分析仪测得A、B两组乐甫波器件的幅频特性曲线如图8所示;采用与表1相同的参数,通过Matlab仿真得到的乐甫波器件幅频特性曲线,如图9所示;对于谐振频率及其相应的插入损耗,实际器件测试结果与数值仿真的对比如表2所示.

图7 乐甫波器件实物图Fig.7 Physical char t about Love wave device

表1 乐甫波器件的几何尺寸Tab.1 Geometric dimension about Lovewave device

表2 实际器件测试结果与数值仿真的对比Tab.2 Comparison of the device's test results and the numerical simulation

通过实际测试结果与数值仿真对比可以看出,仿真计算和实际器件的谐振频率相近,相应的插入损耗也相差不大,表明了本文理论模型的有效性.实验结果与数值仿真还存在着一定偏差,这可能源于器件的装配应力以及测试时的实际温度与理论建模采用的温度(20℃)不一致等原因,需要在今后的研究中加以解决.

薄膜厚度是乐甫波器件的重要参数.当薄膜厚度变化时,器件的幅频特性曲线也会变化,其谐振频率、机电耦合系数和插入损耗都会随之变化,因此在器件设计时需要重点考虑薄膜厚度.数值仿真得出的幅频特性曲线随薄膜厚度的变化如图10所示,谐振频率随薄膜厚度的变化如图11所示,插入损耗和机电耦合系数随薄膜厚度的变化如图12所示.

从图10可以看出,声波器件未加非压电薄膜时,通带纹波的干扰较大.通带纹波指幅频曲线在通频带宽内因为振荡而引起的抖动,通常由器件的三次渡越效应产生.加了非压电薄膜之后,虽然中心频率有所偏移,插入损耗有所增加,但通带纹波的减小非常明显,表明非压电薄膜能够有效地抑制通带纹波,从而在一定程度上改善器件性能.

图8 实际测试的乐甫波幅频特性曲线Fig.8 Actual test's am plitude-frequen cy curve about Love w ave

图9 数值仿真的乐甫波幅频特性曲线Fig.9 Numerical simulation's amplitude-frequency curve about Love w ave

图10 幅频特性曲线随薄膜厚度的变化Fig.10 Amp litude-frequency characteristic curve's change w ith film thickness

由图11可知,谐振频率随薄膜厚度的增加而减小.谐振频率初始时变化不大,在d＞0.63μm之后随薄膜厚度的增加而急剧减小.其原因在于乐甫波的传播速度介于压电基片的表面波速度vs和薄膜介质的体切变波速度vb之间,且随着薄膜厚度的增大由vs趋近于vb.产生乐甫波的条件之一便是,而对于本例中36°YX钽酸锂的压电基片和SU-8光刻胶的薄膜材料而言,vb更是远小于vs.因此,与传播速度的变化一致,乐甫波谐振频率随薄膜厚度的增加而减小.

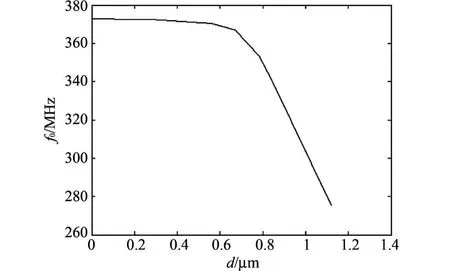
图11 谐振频率随薄膜厚度的变化Fig.11 Resonant frequency's change w ith film th ickness

图12 插入损耗和机电耦合系数随薄膜厚度的变化Fig.12 Inser tion loss and electrom echanical coupling coefficien t's change w ith film thickness

由图12可知,机电耦合系数首先随薄膜厚度的增大而增大,当d=0.63μm左右时达到最大值,之后随薄膜厚度的增大而减小.插入损耗IL随薄膜厚度的增大而增加,其原因在于声场分量随薄膜厚度的增大而远离界面x3=0,声波能量将更多地集中在波导层中,从而降低了声场的压电耦合.当薄膜厚度介于0.4～0.8μm之间时,IL增加的趋势减缓,这是由于该范围内较大,从而在一定程度上补偿了薄膜厚度增大而导致的声场压电耦合降低.

4 结 论

乐甫波是当前声波传感领域的研究热点,对乐甫波器件的幅频特性研究有助于器件的设计、制作及测试系统搭建.本文基于部分波理论和表面有效介电常数方法建立了乐甫波谐振频率的理论分析模型,可以计算出乐甫波的传播速度、谐振频率及机电耦合系数.通过在梅森等效电路中加入波导元件得到了乐甫波器件的等效电路模型,可以仿真出器件的幅频特性曲线.选用 36°YX钽酸锂作为压电基片材料, SU-8光刻胶作为非压电薄膜材料,实际制作了乐甫波器件.通过Matlab仿真得出的幅频特性曲线与器件实际测试结果基本一致,表明了本文理论模型的有效性.本文还仿真了谐振频率、插入损耗和机电耦合系数随薄膜厚度的变化情况,并总结分析了引起上述变化的相应原因,其结论可以为乐甫波器件的设计提供理论指导和仿真依据.

[1] 程利娜,刘明华,李红浪,等.低损耗乐甫波传感器的实验研究[J].仪表技术与传感器,2009(1):122-124.

Cheng Lina,Liu Minghua,LiHonglang,et al.Experimental research of low-loss lovew ave sensors[J].Instrument Technique and Sensor,2009(1):122-124.(in Chinese)

[2] FelicidadeMoreira,Mohamed El Hakiki,Frederic Sarry,etal.Numerical development of ZnO/quartz love w ave structure for gas contam ination detection[J].IEEESensors Journal,2007,7(3):336-341.

[3] Drafts B.A coustic wave technology sensors[J].IEEE Transations on Microwave Theory and Techniques,2001,49(4): 795-802.

[4] Lin Fanchi,MoschettiMorgan P,Ritzw oller MichaelH.Surfacew ave tomography of the western united states from ambient seism ic noise:rayleigh and love w ave phase velocitymaps[J].Geophysical Journal International,2008,173(1):281-298.

[5] Tiersten H F.Linear Piezoelectric Plate Vibration[M].New York:Plenum Press,1969.

[6] 陈智军.声板波激发特性与液体传感研究[D].上海:上海交通大学,2007.

[7] Nay feh A H.Wave Propagation in Layered Anisotropic Media[M].Amsterdam:North-Holland,1995.

[8] 张小宁,陈智军,宣建青,等.乐甫波传播特性研究[J].压电与声光,2011,33(2):174-177.

Zhang Xiaoning,Chen Zhijun,Xuan Jianqing,et al.Research on propagation characteristics of Love wave[J].Piezoelectrics&A coustooptics,2011,33(2):174-177.(in Chinese)

[9] Smith WR,Gerard H M,Collins JH,etal.Analysis of interdigital surfacew ave transducers by useof an equivalent circuit model[J].IEEE.Trans.on Microwave Theo.and Tech.,1969,17(11):856-864.

[10] Kalantar-zadeh K,WlodarskiW,Galatsis K.An Equivalent Circuit for Simulating Love Mode A coustic Wave Transducers:Comparison of Simulation and Experimental Results[C].Australia,Melbourne,2000:371-374.

[11] 毛伟.声表面波传感器及其接口设计的研究[D].杭州:浙江大学,2006.

[12] Kalantar-zadeh K,WlodarskiW,Galatsis K.Simulation of a LoveMode Surface Acoustic Wave Transducer[C].Proceedings of IEEE Ultrasonics Symposium,Lake Tahoe,USA,October 1999,Symposium Proceedings,1999:161-164.