《数根丛草》注记

李兆华

(天津师范大学数学科学学院，天津300387)

素数，早期译为数根。数根一词始见于《数理精蕴》(1723)下编卷38。李善兰(1811～1882)、伟烈亚力(A.Wylie，1818～1887)译《几何原本》后九卷(1857)沿用数根一词，见该书卷7。中国传统数学没有给出素数的概念。晚清的数学家比较关注素数的研究并给出若干有意义的结果。其中，李善兰《考数根法》(1872)与方士①方士，字梅荪，湖北天门人，生卒年代不详。《数根丛草》卷首校算人名有门人周国柱等。李迪《中国算学书目汇编》载，“《南郡书院算学课艺》，(清)方梅荪阅定，周国柱编次”，光绪二十六年刊本，未见传本。南郡谓施南府，治今湖北恩施县。王同愈(1856～1941)《栩缘日记》卷2光绪二十六年九月十六日记，“施南府县来电云:方山长士，有品无行，即复电。”王氏时任湖北学政。见顾廷龙编《王同愈集》，上海古籍出版社，1998年。《数根丛草》(1897)是晚清讨论素数判别法的两部主要著作。《考数根法》［1］是国人论述素数最早的工作。光绪二十二年(1896)夏，因门人请教《考数根法》，方士遂有《数根丛草》［2］之作。余经华为之补草。

《考数根法》的主要结论可表述如下。设N，a是正整数，(N，a)=1。求得最小正整数d②《考数根法》共给出十八个例题，所得d不都是最小的。例如“准根分级法”第四例，N=14209，a=2，求得d=6720。第五例，N=16637，a=2，求得d=8190。两例中的d均非最小。参见下文。使得

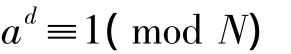
d称为“定次”。N为素数的充分与必要条件是，d整除N-1，且kp+1不整除N。其中，k，p是正整数，p整除d。［3］显然，该法的关键是求得d。《考数根法》给出四种求d的方法，即“屡乘求一法”、“天元求一法”、“小数回环法”及“准根分级法”。［4］①严敦杰“中算家的素数论”一文所引“准根分级法”术文有误。应据《中西闻见录》第4号原文改正。设(N，a)=1，N是素数，则aN-1≡1(modN)。此即费尔马小定理(1640)。李善兰上述结论的实质是，将费尔马小定理中的必要条件加强，使成为充分与必要条件。这一结论说明李善兰对费尔马小定理的深刻认识。至于求d四法，前二法较后二法为上。“小数回环法”，用的纯循环小数的循环节长度d判别N是否素数，只是举例说明并未阐述理由。“准根分级法”，用“超乘补乘”求d，当不能求得d时又借助“天元求一法”另行计算，尚非完整的方法。《考数根法》具有重要价值，亦有不足之处。

《数根丛草》共给出20术，每术之后均有例题。术文与例题结合，说明判别N是否素数的方法。在这20术中，第6术、第10术与第11术的理论有误;第12术与13术实用价值不大;②第12术可表述为，设N＞1是正整数，N为素数的充分与必要条件是(N-1)!≡-1(mod N)。第13术据此用对数计算。计算量非常大。设N是一个3位数，则(N-1)!+1超过100位数。见李文林主编《王元论哥德巴赫猜想》，山东教育出版社，1999年，第108页。第1术、第4术与第5术用最小素因数试除法，理由比较明显，③若N＞1是合数，则N的最小素因数列出这些素因数逐一试除N。当N很大时，满足条件的素因数约为个。等等。除此之外，《数根丛草》比较重要的术文包括:第2术，第7至第9术，第14术，第17至第20术。此9术中，第14术与第19术，第18术分别是李善兰“小数回环法”与“准根分级法”的完善，其他6术是因数分解判别素数法的运用。《数根丛草》的内容选择与文字表述不如《考数根法》精审，而初等数论的知识与方法超出《考数根法》者亦复不少。

关于《数根丛草》的讨论并不多见，目前主要有“《数根丛草》研究”［5］一文。该文最早指出，第12术是威尔逊(J.Wilson，1741～1793)定理，④威尔逊定理:若p是素数，则(p-1)!≡-1(mod p)。方氏第12术是一个充分与必要条件。在初等数论中，这是两个定理。M.克莱因《古今数学思想》称后者为威尔逊定理。见该书第2册第367～368页，上海科学技术出版社，1979年。“《数根丛草》研究”一文的称谓同该书。本文沿用这一称谓。并认为方氏独立得到这一定理;并且指出，第10术、第11术误以为费尔马小定理的逆命题为真，重复了华蘅芳(1833～1902)的错误;同时就第6术等若干术文给出解释。这一工作使得《数根丛草》的内容引起关注。就术文的解释而言，该文尚有错误和遗漏。本文基于《数根丛草》与《考数根法》的联系，重点考察《数根丛草》第2术等9术的内容，就其中因数分解判别素数法的运用、“小数回环法”与“准根分级法”的完善等两项工作的数学意义予以分析，补正以往解释的某些错漏，从而说明晚清数学家认识与运用素数判别法的水准。为叙述的方便，术文的顺序作了调整，原有序号一并标出。文中的例题除一例之外均选自《考数根法》与《数根丛草》。

1 因数分解判别素数法之运用

第7术:

先取略大于本数之一个平方积，与本数相减，为余实。乃以所取之平方根倍之加一，以加余实，视其能否成方积。不成，又加倍平方根加三。不成，又加倍平方根加五。于是屡加，至适成一个正方积而止。乃以所成之方根为半较，加本数开平方之根为半和，以和较相加减，即得大小乘数。如所加之数已近本数折半自乘之数，则不必求乘数，即知本数是数根。

记本数为N，取x使x2＞N，x2-N为余实。依次计算

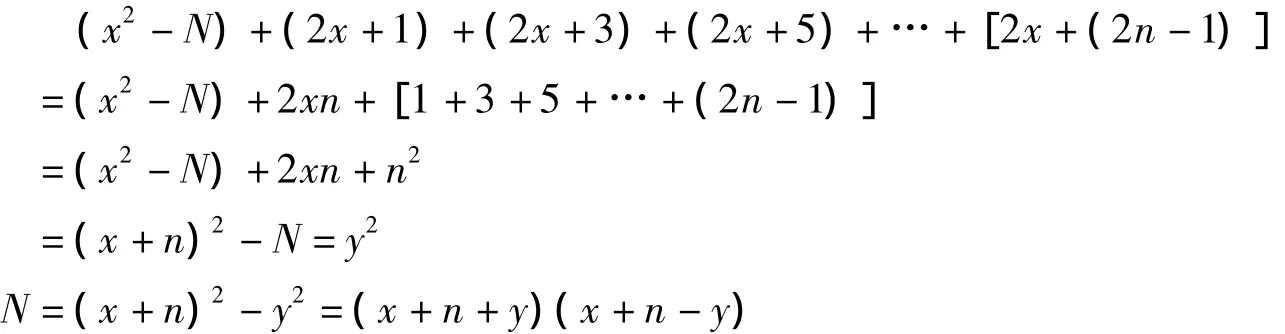
由初等数论知，设N是奇数，a＞b，若

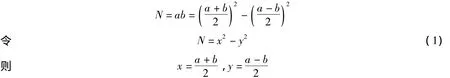
由式(1)求得x，y，即可求得因数a，b:

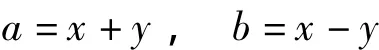
其中，x，y一奇一偶。若N是奇素数，则N能且仅能表为

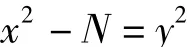
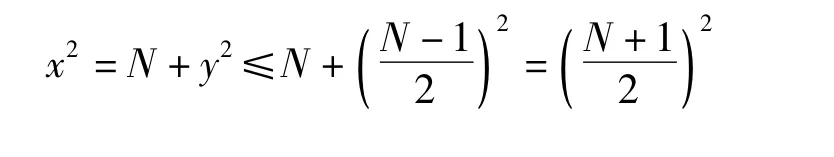
故式(1)中x的取值范围是

在第7术中，因每步增加的值分别为2x+1，2(x+1)+1，2(x+2)+1，…，2(x+n-1)+1，故其演算采用以下两例的格式较为简便。

判别N=1891是否素数。

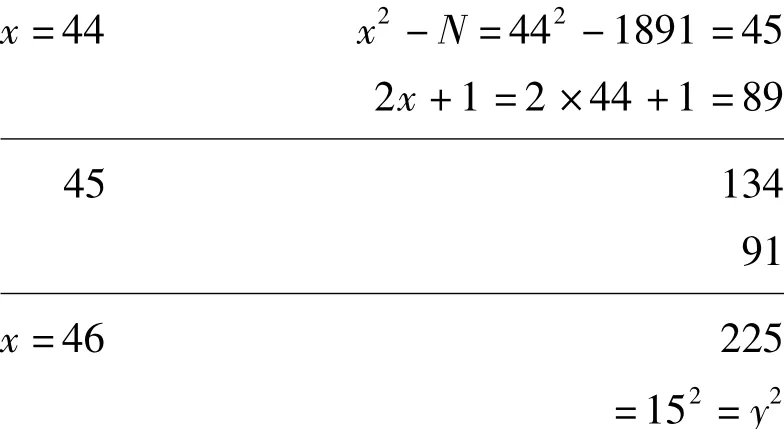
由x2-N=y2，即

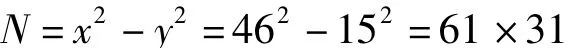
可知，N=1891不是素数。

判别N=31是否素数。

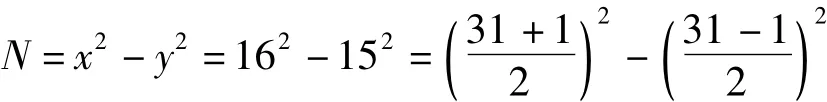
由x2-N=y2，即由式(2)，可知，N=31是素数。

第7术与费尔马因数分解判别素数法(Fermat's factorization method)相同。［6］

第8术、第9术与第7术同义。第8术用

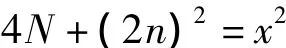
术文“如所加之平方根已大于本数，则知本数是数根。”所加之平方根即(2n)。由式(3)，准确的表述当为“如所加之平方根已等于本数减一，则本数是数根。”第9术用

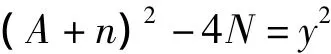
第6术:

置本数加一开平方。不尽，又加一个八开之。不尽，又加二个八开之。不尽，又加三个八开之。于是屡加，至开方适尽而止。乃以开得之数为半和，所加之平方根为半较，和较相加减，即得大小两乘数，则知本数必非数根。如果所加之平方根已与本数折半之数相近，而仍不能开平方，或开方之数等于本数加一折半之数，则知本数是数根。

本术有误。记本数为N。若N不是素数，依术当有

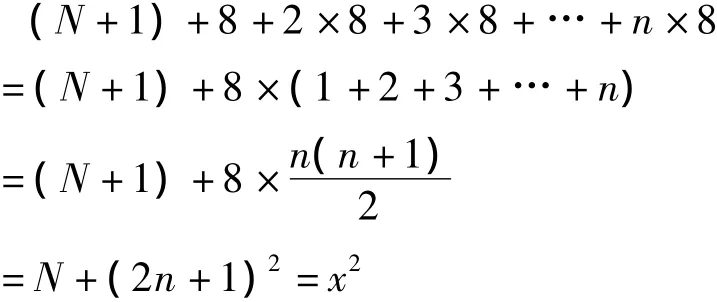
事实上，这个等式不一定成立。由式(1)可知，x，y一奇一偶，即y可奇可偶。若规定y=2n+1，则N+(2n+1)2不一定是完全平方数。例如，N=221=17×13。若

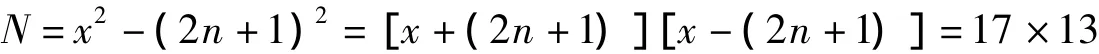
则

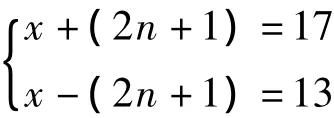
解得x=15，(2n+1)=2。但(2n+1)是奇数。矛盾。因而，第6术是错误术文。

［5］没有指出这一错误，反将第6术列为“独创的素数判别法”予以解释和肯定。

第20术:

置本数开平方，不尽，余负实。以开得之数为大方根。又以负实开方为小方根，余正实。倍大方根加一，以减正实，余负实。倍小方根，除之为第一数，加于倍小方根内，以乘第一数，与负实相加，余正实。倍大方根加三减之，余负实。倍小方根内加倍第一数，除之为第二数，相加，以第二数乘之，与负实相加，余正实。又倍大方根加五减之，余负实。如是屡减屡加，至余实恰尽而止。如大方根已至本数六［二］①原文六分之一，误。以第6术、第7术例此，当作二分之一，盖二与六行书字形相近而误。分之一而仍不尽，则知本数是数根。如能恰尽，则以所加之大方根为半和，所加之小方根为半较，半和较相加减，即得大小乘数，则知本数非数根。合问。

记本数为N，x为大方根，-ri为余负实，y为小方根，+si为余正实，i=0，1，2，…，n。依次计算

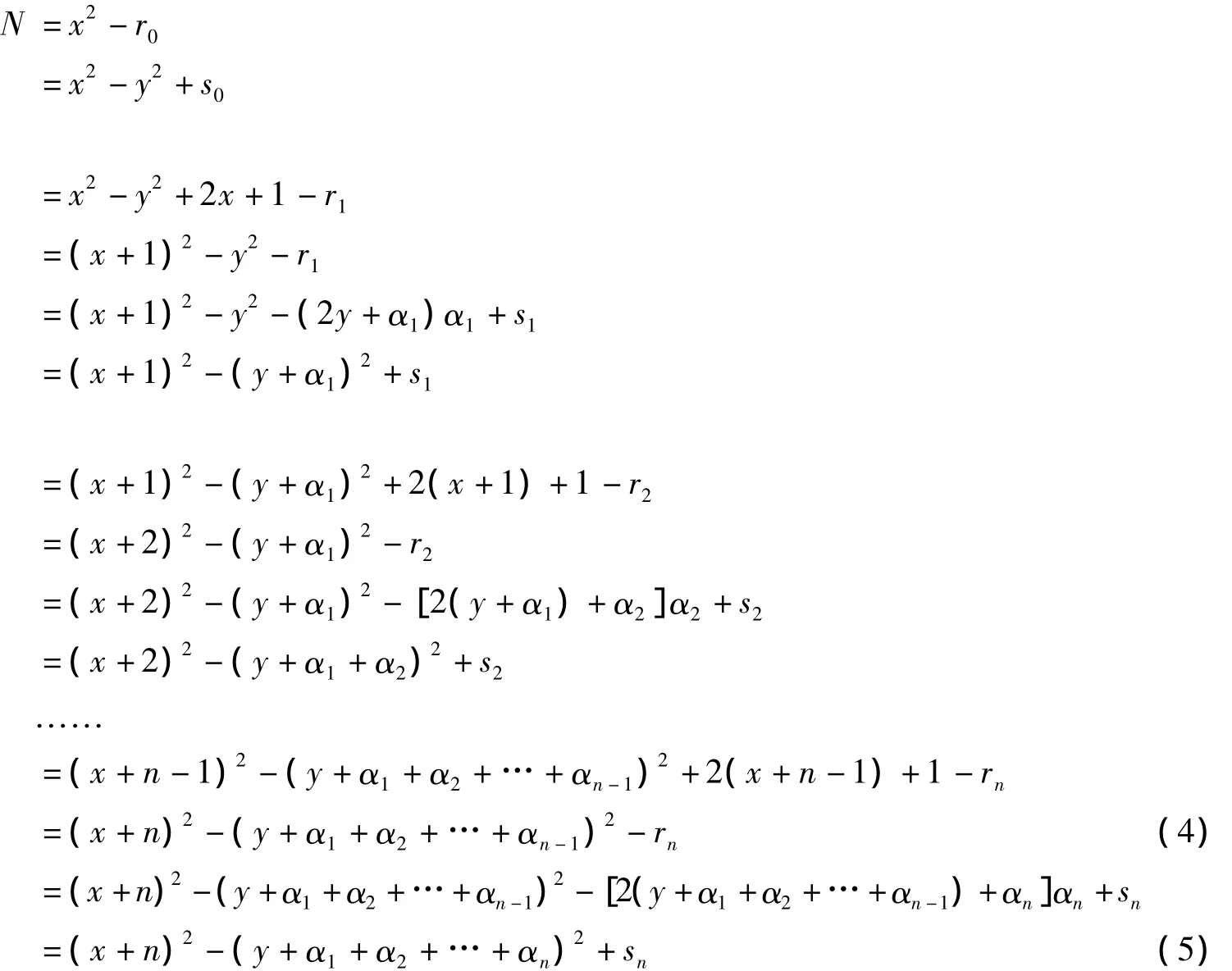
其中，

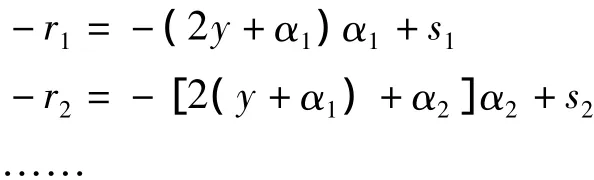
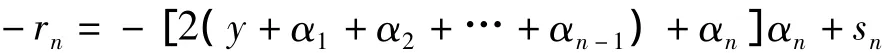
由此可得

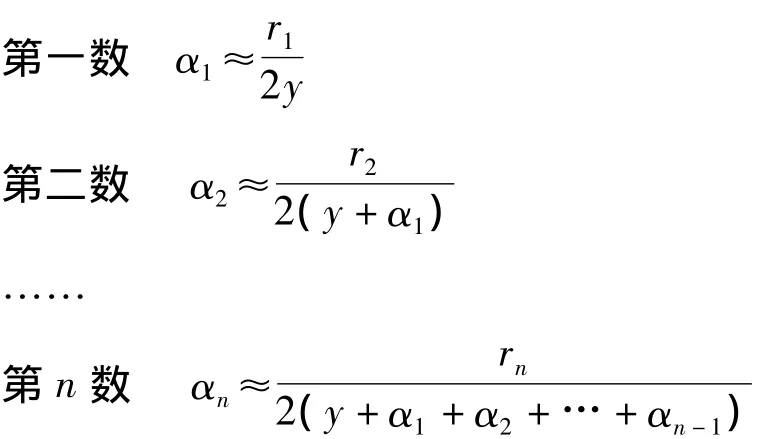
在式(4)中，若rn=0，则

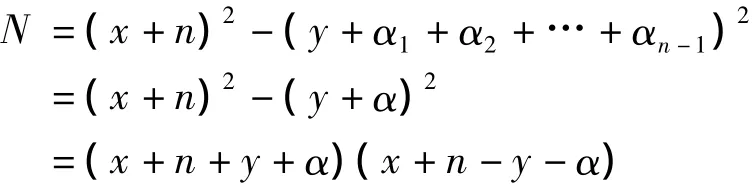
在式(5)中，若sn=0，则

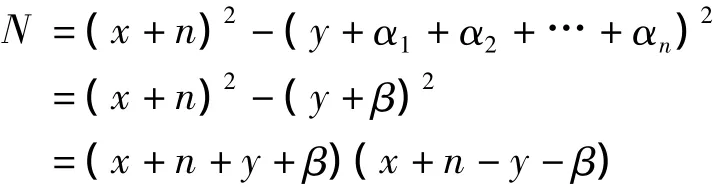
可知，N不是素数。

若rn≠0，当时，由式(4)必有

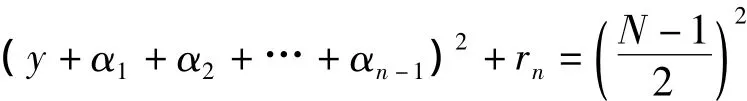
若sn≠0，当时，由式(5)必有

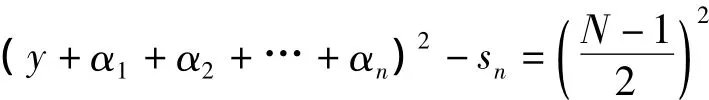
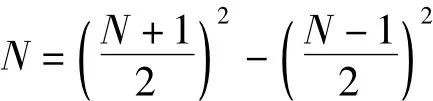
由式(2)，可知，N是素数。

第20术与第7术同义，唯第7术的变元是x，而第20术则为x，y。术文“如大方根已至本数六［二］分之一而仍不能尽，则知本数是数根”，乃约略之言。大方根即(x+n)。由式(3)，准确的表述当为“如大方根已至本数加一折半自乘，减本数开方适尽，则知本数是数根”。

参考文献［5］遗漏rn=0的情况。原文“已至本数六分之一”，于理不通，当校而未校，结论“若……已近而sk+1≠0，……知N为数根(素数)”随之而误。

第17术:

先取略近本数之一个方根。以除本数，得数与方根相减为根较。余负实若干置于下。任取一个奇数以加根较，①“根较”原文误作“方较”。上文作“根较”，据改。仍与奇数相乘，得数以减负实，视其恰尽否。不尽，又以奇数减方根为法，除本数，如前求之，至屡求恰尽而止。即以其法为小乘数。如法已为三，而仍不能尽，则知本数是数根。

本条术文稍嫌简略，须结合例题方可了解术意。记本数为N，取x1为偶数以x1除N求得正整数称为根较，ri称为余实，i=1，2，3，…，n+1。余实可正可负，术文以余负实为例。依次计算

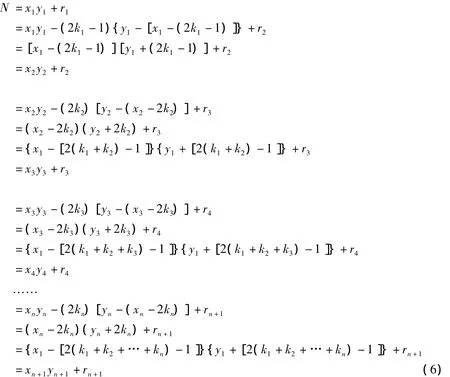
判别N=7081是否素数。

原草如下。取x1=84，得y1=85，r1=-59。依次计算

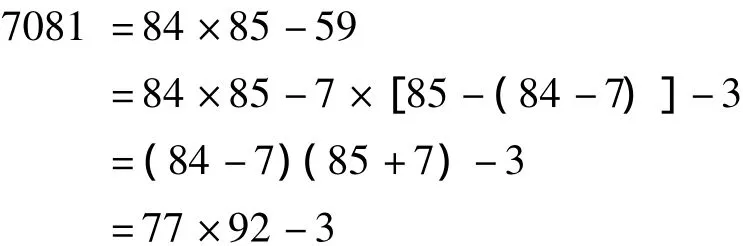
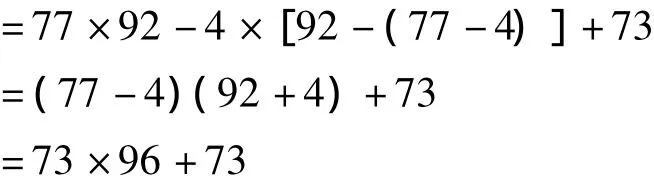
而

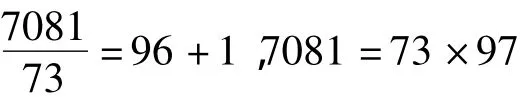
可知，N=7081不是素数。

依术文所说，“任取一个奇数以加根较，仍与奇数相乘”，即上式7×［85-(84-7)］之中的奇数7为“任取”。例题演草所说，“任于七十七之内减一偶数四”，即上式4×［92-(77-4)］之中的偶数4为“任减”。奇数7与偶数4分别对应上述k1=4，k2=2。这种“任取”具有偶然性。例如，将奇数7代之以9，偶数4不变，即k1=5，k2=2，则不能得到分解7081=73×97。为了避免“任取”，可令k1=k2=k3=…=kn=1。虽计算次数增加，但不致出现遗漏。仍用上例，逐步计算，所得结果相同，具体演算从略。

事实上，令k1+k2+k3+…+kn=k，式(6)变为

或即

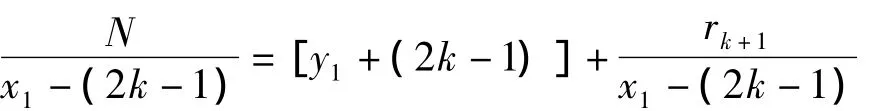
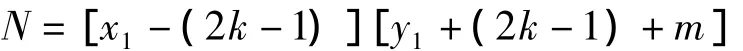
可知，N不是素数。若对任一k，［x1-(2k-1)］不整除rk+1，则N是素数。

在上例中，x1=84，y1=85，取k=6，得7081=73 ×97。

第2术:

记本数为N，①原文“巳”字对应英文字母p。此处记作N以求上下文符号一致。以为平方之限，依次求得余数即

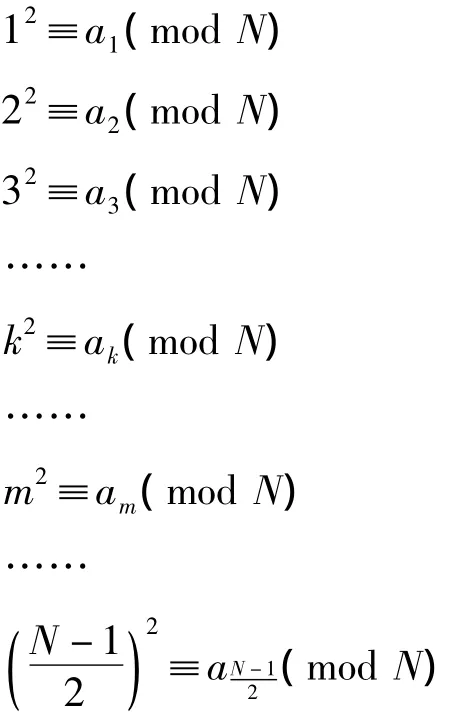
若am=ak，则自am+1起不再计算。此时，

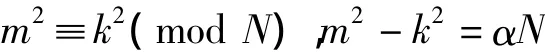
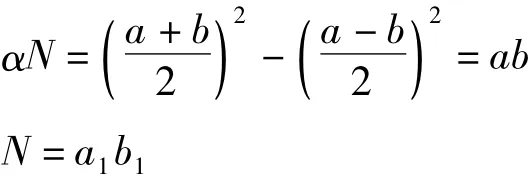
可知，N不是素数。

判别N=51是否素数。

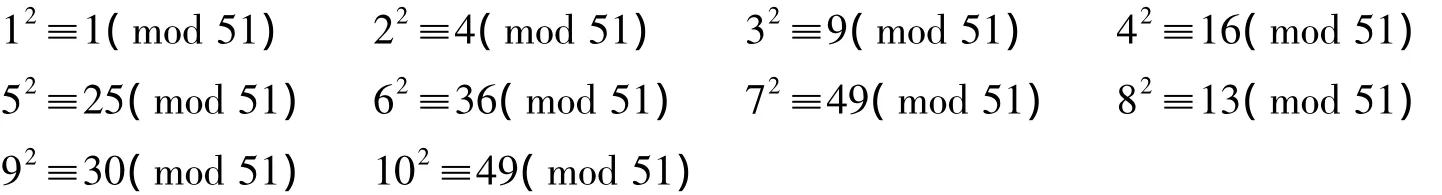
余数49重复出现。此时

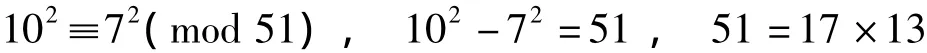
可知，51不是素数。

由初等数论知，设(N，a)=1，二次同余式

有解或无解。若式(8)有解，则a称为模N的平方剩余。若式(8)无解，则a称为模N的平方非剩余。当N是奇素数时，模N的简化剩余系中，平方剩余与平方非剩余的个数各为个。且个平方剩余分别与之中一数且仅与一数同余。［7］据此，将依次代入式(8)，求得余数此时，，且

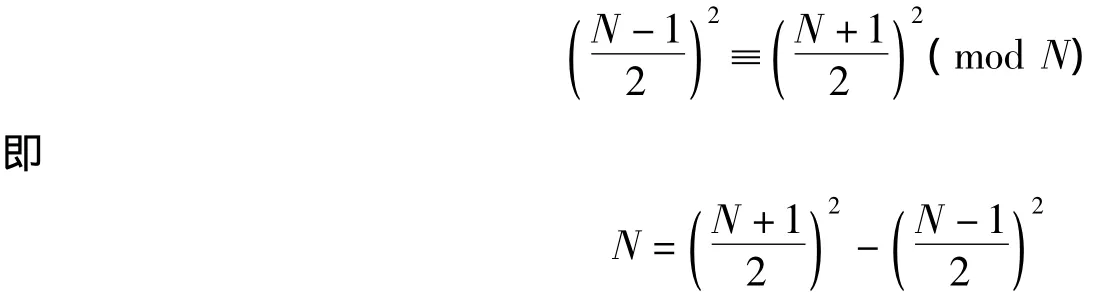
当N不是素数时，设N=N1N2，N1，N2＞1 是奇素数。将x=1，2，3，…，(N-1)依次代入式(8)，求得余数a1，a2，a3，…，aN-1，删去(N，ai)≠1 的各数，满足式(8)条件的余数共有

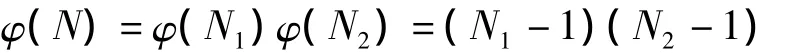
个。φ(N)是欧拉函数，表示模N简化剩余系中正整数的个数。由二次同余式解的定理知，此时式(8)有4个解。故式(8)的平方剩余只有

)个。又因

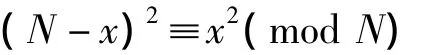
当N=N1N2N3…Nk时，Ni＞1是奇素数，有类似的结论。

数N的平方剩余不会重复出现，反之亦然。故当平方剩余重复出现时，即可判定N不是素数。

若am=ak，则由

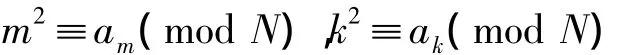
将N分解为乘积形式。

用上述结论检验原例N=51的分解过程如下。

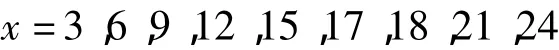
等9个数时，a的值分别是

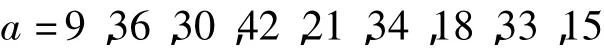
此时，(51，a)≠1，删去之，还有如下16 式

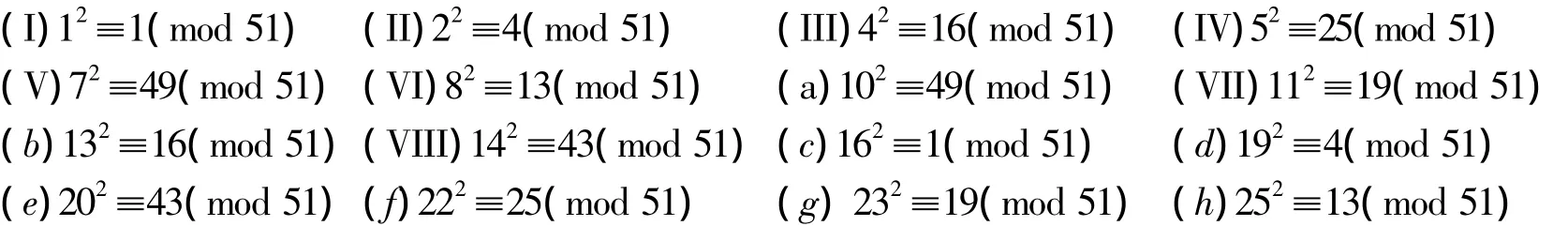
在以上16式中，余数a均满足条件(51，a)=1，余数的个数为

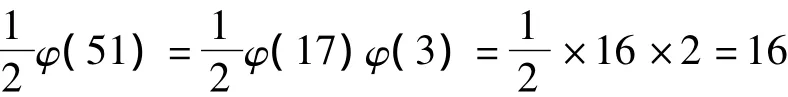
其中，平方剩余的个数为

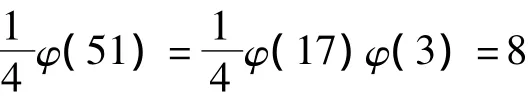
每个平方剩余重复出现2次。分解N=51的方式共8种，分别是

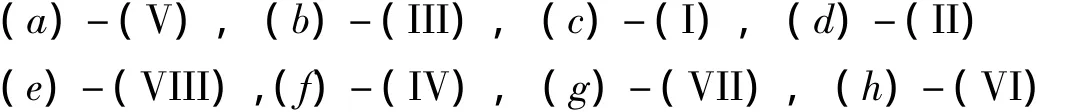
由其中任一方式均可将N分解。例如，由(b)-(III)有

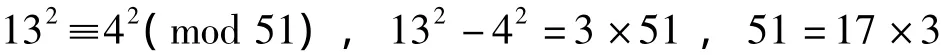
因而，只要平方剩余重复出现，即可据以分解N。以上例而言，只需式(a)出现即可，式(VII)以下无需计算。

该术运用平方剩余概念作因数分解以判别N是否素数，然而术文殊欠完整。“无相同之余数”的情形，该术未予说明。此外，计算亦欠严谨。原例所给10个余数中，余数9，36，30当删而未删。

参考文献［5］称该术“利用了这样的事实:模p的简化剩余系中，平方剩余与非平方剩余的个数各为由以上所述可见，该术只论N不是素数的情形，并未利用所指的事实。引文亦须说明，模p为奇素数。否则，命题不真。此外，参考文献［5］取x0“使其是相同数之剩余数，这样就必有t2=x0，…”，似有误文。

2 “小数回环法”与“准根分级法”之完善

第19术:

将本数之各倍一一列于右，另以一与本数之各倍两两相加，视其得若干次复变为一。乃以其次数约本数，是否余一。否，则本数非数根。是，则即以其奇数倍之为递加数，加一，除本数。不尽，又加一个递加数，除之。如是屡加至得数小于法，仍不尽，则知本数是数根。

记本数为N，依次计算

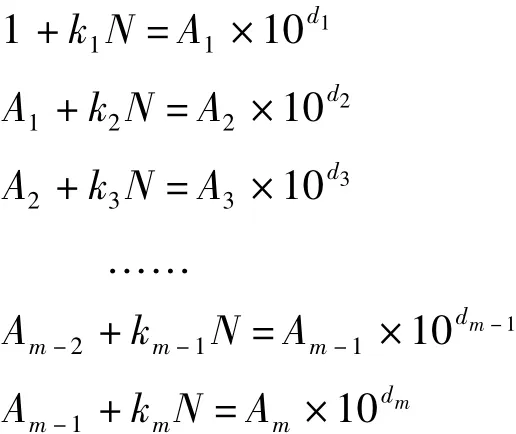
其中，ki N是本数的各倍数，1≤ki≤9是正整数，Ai=ai1ai2ai3…aij是个位数aij≠0的正整数，i，j=1，2，3，…。当Am=1 时，计算过程结束。此时，d=d1+d2+d3+ … +dm为所求的次数即定次。据此，用李善兰的结论判别N是否素数。

事实上，由上列各式可得，

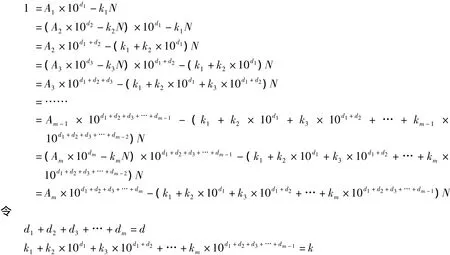
又Am=1，故

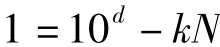
即

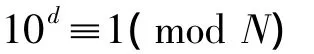
因而，d=d1+d2+d3+…+dm为所求的定次。

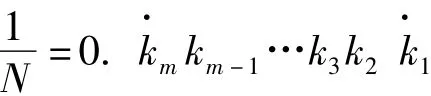
求其第一个循环节的除法计算过程。例如，

由此除法算式逆推可得

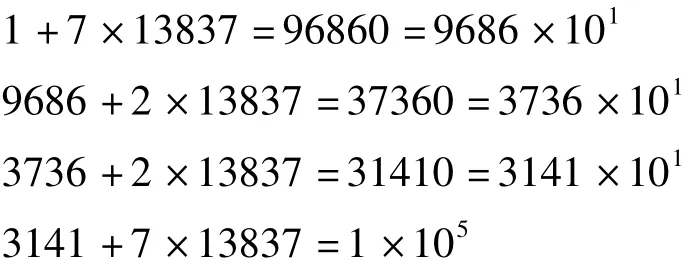
故d=1+1+1+5=8。第19术即这一计算过程的一般表述。化为纯循环小数的充分与必要条件是(N，10)=1。只有N满足这一条件必能化为纯循环小数，从而得d。当N是奇素数时的循环节长度等于N-1，或m，且m整除N-1。因而，可以借助循环节长度以判别N是否素数。

第14术:

置本数减一，以十约之。不尽，加若干个本数约之为第一数，又将第一数以十约之。不尽，内加若干本数约之为第二数，如是屡约，至第几数始为一，或等于本数减一。乃计所约若干次。如末数为一，则将次数倍之为方指数。如末数为本数减一，即以次数为方指数。于是，以方指数为递加数，加一除本数。不尽，又加一个方指数除之。依此屡加除之，视其能尽者，则本数非数根。不尽者，本数是数根。记本数为N，(N，10)=1。①术文未明确这一条件。例题满足之。依次计算

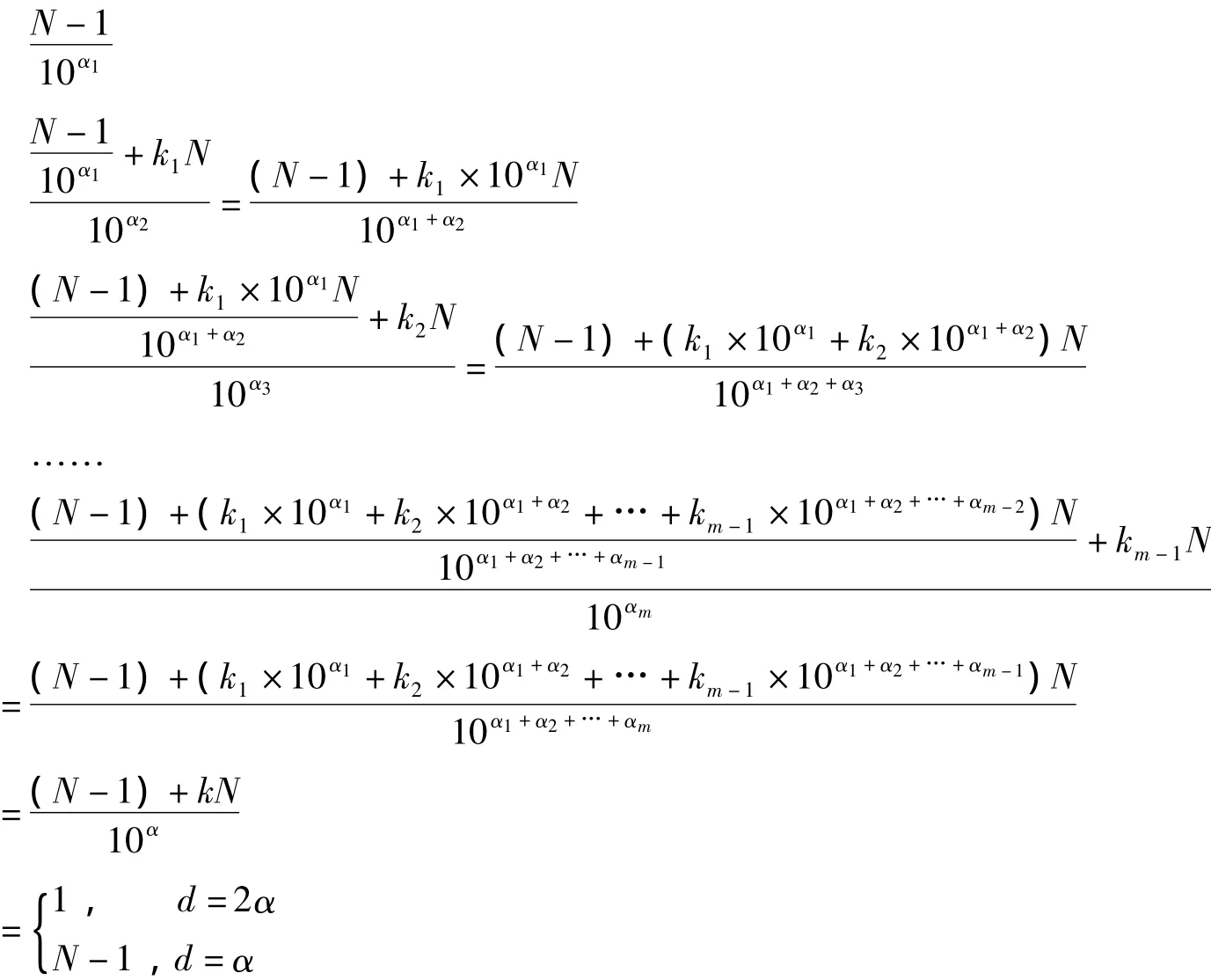
据此，用李善兰的结论判别N是否素数。①当d=2α时，只用即可判别N是否素数。参见原书例题其中，

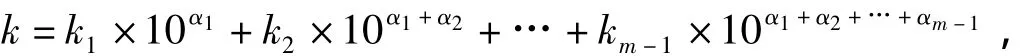
α =α1+α2+… +αm，1≤ki≤9 是正整数，αi=0，1，2，…，i=1，2，3，…，m。事实上，若

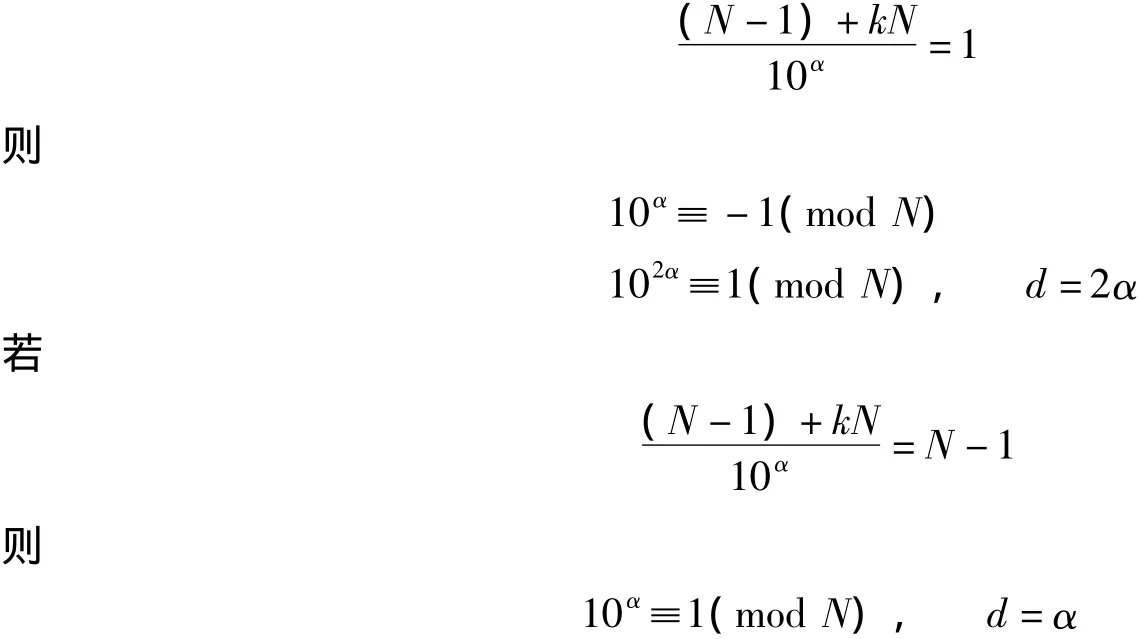
由此可知，该术给出满足条件

的d的一种算法。其中表为纯循环小数的充分与必要条件的另一表述是，其循环节长度d满足式(9)。

以上两术是李善兰“小数回环法”的进一步完善。李氏以具体的例题说明循环节长度d可用除法求得。而后，以d判别N是否素数。其术缺少一般性的表述及必要的理由。②李氏原术谓“其回环数有正负相间者，有有正无负者”，意义不明。华蘅芳《算草丛存》之七“循环小数考”称“惟言回环数有正负相间者尚未考得。”兹仍存疑。比较之下，《数根丛草》第19术与第14术方法更为完整。

第18术:

置本数减一折半为方准。视其内有若干乘数，先取最大之一个乘数为约法之次数。乃置本数加一，以二约之，得数，又以二约之。不受约，又加一个本数约之。如是屡约，至适满所定之次数而止。查其余数是否为一。是，则即以其次数为递加数，以除本数。不尽者，是数根。否，则再以次大数减一，乘最大数为约法之次数。如前法约之。至所约之次数已满方准，仍不余一，则知其数非数根。若未满次数以前能得余数为一，则其数亦非数根。

记本数为N，

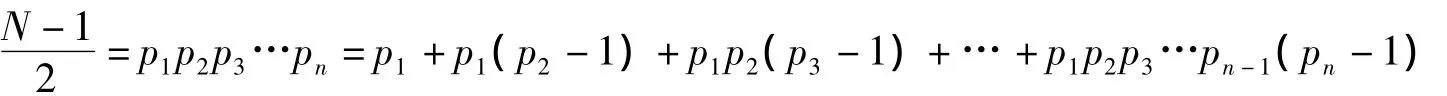
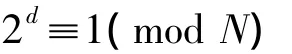
中的d。若等于d，即d整除方准，此时称d“适满所定(约法)之次数，余数为一”。由此可知，N可能是素数，因d整除N-1。若“所约之次数已满方准，仍不余一”，即的任一个素因数或其相乘积均不等于d，依术可得除的素因数或其相乘积之外的满足上述条件的d，即d不整除方准，此时称d“未满(所定约法之)次数，余数为一”。由此可知，N不是素数，因d不整除N-1。

为求得满足条件的d且使的素因数或其相乘积不致遗漏，计算以约法之次数为序分段进行，直至约得结果等于1或N-1为止，①术文“查其余数是否为一”包括等于1或N-1两种情形。参见该书第3术及其例题。即得所求的d。

据此，用李善兰的结论判别N是否素数。②当时 d=2α，只用即可判别N是否素数。参见后例其中，

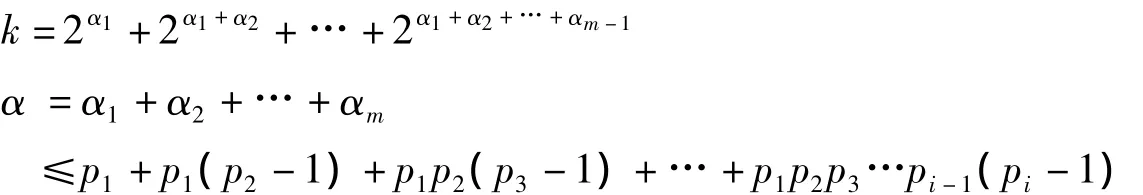
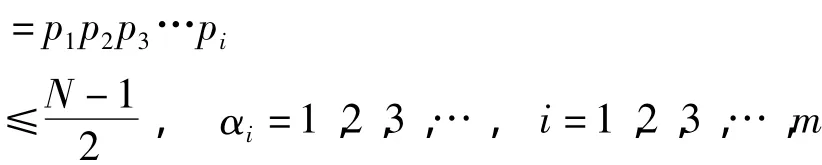
该术求d的方法与第14术相同。以下举例说明其应用。

判别N=37是否素数。①本例不在《考数根法》与《数根丛草》之中。

第1段，以p1=3为约法之次数，依次计算

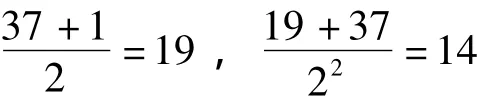
1+2=3=p1，余数不得 1。

第2段，以p1(p2-1)=6为约法之次数，依次计算

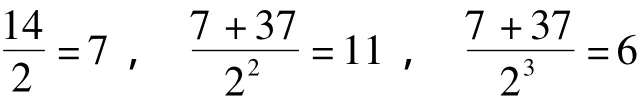
1+2+3=6=p1(p2-1)，余数不得1。

第3段，以p1p2(p3-1)=9为约法之次数，依次计算

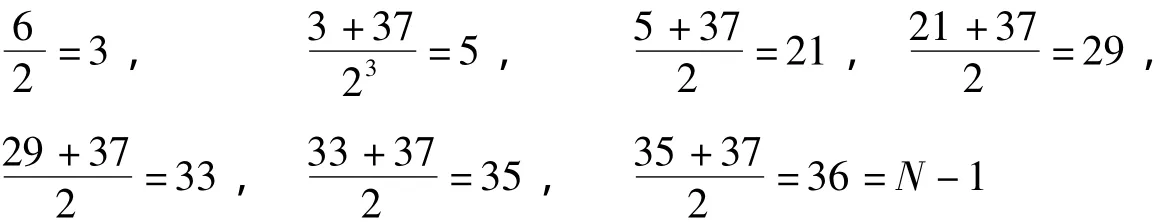
1+3+5×1=9=p1p2(p3-1)，余数得N-1。

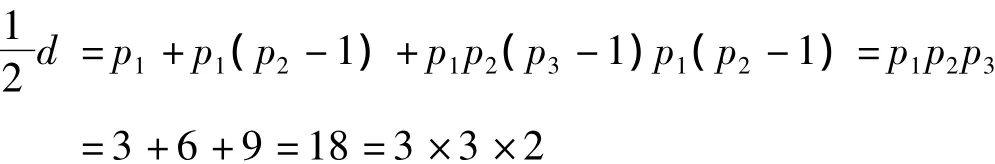
整除方准，N=37可能是素数。且，得数5已小于除数7。N=37是素数。

判别N=341是否素数。

第1段，以p1=17为约法之次数，依次计算

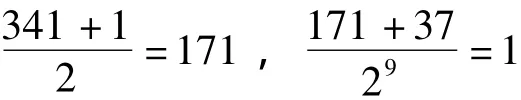
1+9=10=5 ×2=p2p3，余数得1。

d=p2p3=5×2，整除方准，N=341可能是素数。但不是素数。

判别N=91是否素数。

第1段，以p1=5为约法之次数，依次计算

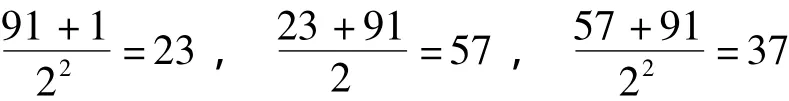
2+1+2=5=p1，余数不得 1。

第2段，以p1(p2-1)=10为约法之次数，依次计算

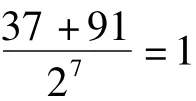
7不满约法之次数p1(p2-1)=10，余数得1。

d=p1+7=5+7=12=3×2×2，不整除方准，N=91不是素数。

该术是李善兰“准根分级法”的进一步完善。李善兰用“超乘补乘”求d，此处改用“累加累除”求d。当N是多位数时，用超乘补乘虽较简便，但下列两点亦属明显的不足。其一，求得

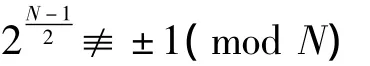
时，虽可判别N不是素数，但因未能求得d而无法给出N的因数分解。为了分解N，李善兰借助“天元求一法”另行求d。其二，虽可避免遗漏整除方准的d，但可能遗漏不整除方准的d。因而“准根分级法”不是一个完整的方法。李善兰就其法给出五5个例题。第5例是判别N=16637是否素数。李氏给出

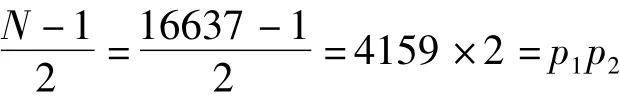
用超乘补乘求得

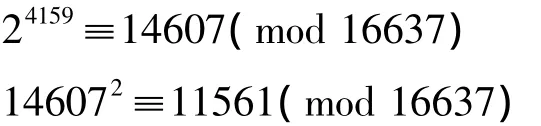
从而

显然，4159×2=p1p2，已满所定之次数，而余数不得1。据此，仅能判别N=16637不是素数，而不能给出N的因数分解。“欲知本数之根，当以大衍术入之。”李氏另用天元求一法解

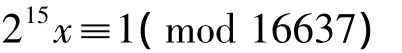
得x=4636，即

再以4636为乘法，求得

由式(11)得

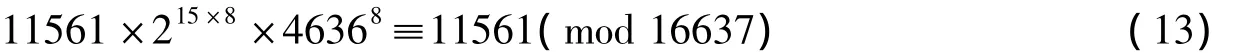
由式(12)得

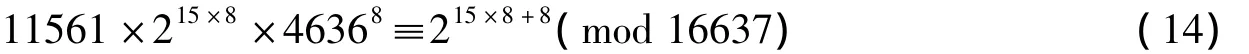
由式(13)、(14)得

由式(10)、(15)得

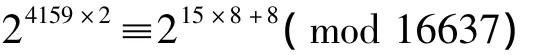
即

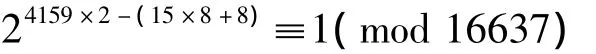
由此可得

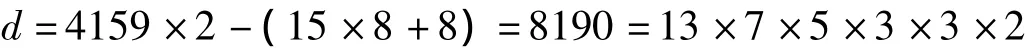
最后，取d分解

方氏第18术的关键是以“累加累除”求得d。方准之设以及分段计算只为避免遗漏整除方准的d。不设方准亦不用分段，连续运用“累加累除”即可求得d。仍以N=16637为例:①本题共迭代455次，计算由研究生刘轶明完成。

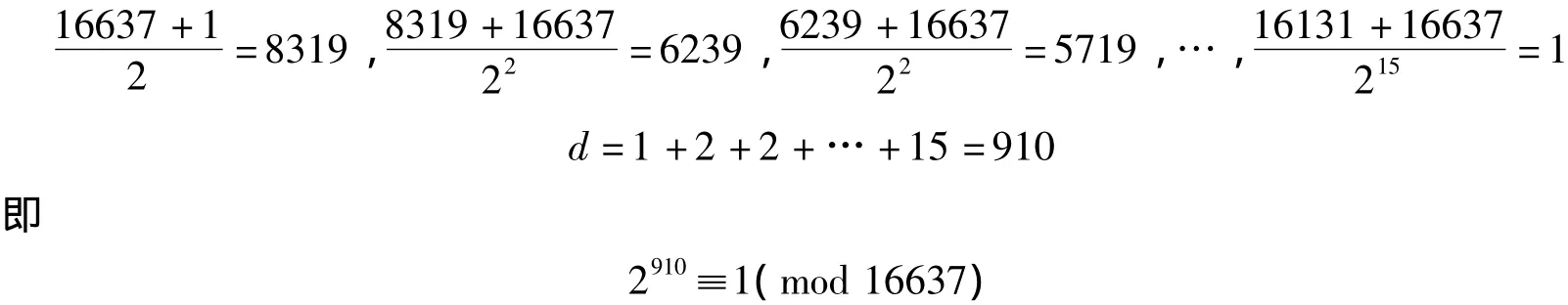
取d=910=13×7×5×2，分解N的结果同前。李善兰用“超乘补乘”计算，因而遗漏了不整除方准的d=910。其所得d=8190=910×9，显非最小。比较之下，方氏第十八术虽计算次数较多，但确是一个完整的方法。参考文献［5］遗漏了约得结果等于N-1的情形。若遗漏这种情形，则需要继续“累加累除”方可求得1，从而使得计算次数成倍的增加。参见上述N=37的情形。

3 《数根丛草》两项工作的简短分析

如前所述，《数根丛草》的内容选择与文字表达均存在不足。然而，在因数分解判别素数法的应用、李善兰“小数回环法”与“准根分级法”的完善等两方面给出较为深刻的工作。其中可以第7术、第17术、第19术及第18术为代表。

因数分解判别素数法是一种常用的方法。设N=ab，a＞b。当a-b较小时，用第7术较为简便。当a-b较大时，用第17术较为简便。兹以第7术为例说明之。

李善兰“准根分级法”第4例N=13447，给出

取d=6720=168×40，判别知N=13447=119×113，不是素数。由方氏第18术可得

取d=168，判别结果同前。“累加累除”所得d值为“超乘补乘”所得d值的，而计算次数则为74次。若改用方氏第7术则极为简单。

判别N=13447是否素数。

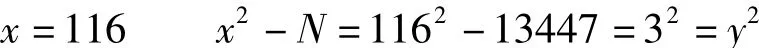
由x2-N=y2，即

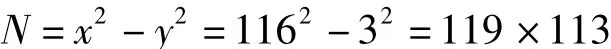
可知，N=13447不是素数。

又如，上述李善兰“准根分级法”第5例N=16637，给出

取d=8190=910×9，判别知N=16637=131×127，不是素数。由方氏第18术可得

取d=910，判别结果同前。“累加累除”所得d值为“超乘补乘”所得d值的，而计算次

数则为455次。若改用方氏第7术则极为简单。

判别N=16637是否素数。

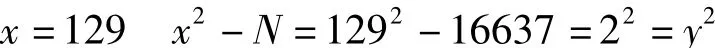
由x2-N=y2，即

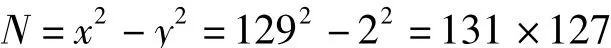
可知，N=16637不是素数。

以上两例均为两个因数之差a-b较小的情形。若N的两个因数差较大，或N为素数，则因数分解法的计算次数随之增加。

以李善兰的结论判别N是否素数，须先求得d。求d的方法不同，所得d值大小亦即计算次数可能有明显的差别。

例如，李善兰“屡乘求一法”第1例N=31，给出

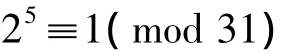
取d=5，判别知N=31是素数。若改用“小数回环法”可得

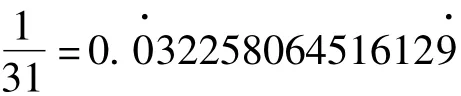
或即

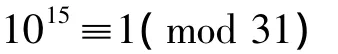
取d=15=5×3，判别结果同前。计算次数相差明显。

再如，李善兰“小数回环法”第1例N=271，给出

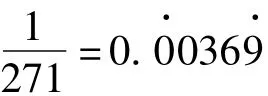
或即

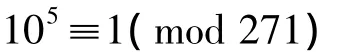
取d=5，判别知N=271是素数。若改用“天元求一法”可得

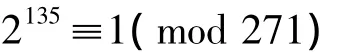
取d=135=5×27，判别结果同前。计算次数相差明显。

又如，李善兰“天元求一法”第2例N=63973，给出

取d=18，判别知N=63973=9139×7，不是素数。若改用方氏第18术可得

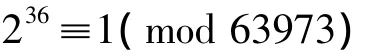
取d=36=18×2，判别结果同前。计算次数相差明显。

此外，上述李善兰“准根分级法”第5例N=16637，用“累加累除”与“超乘补乘”分别求得

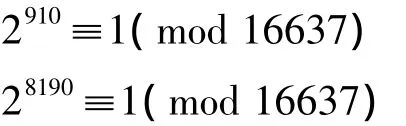
亦属此类情形。

以上4例可以说明，不同的求d方法各有所用，不可偏废。然而，对于给定的N，选择何种方法求得d，事先难以预知。试算是不可缺少的工作。《考数根法》求d四法之下所设各例当是试算之后的安排。因而，以李善兰的结论判别N是否素数，建立完整、简便的求d方法至为关键。“小数回环法”与“准根分级法”的完善，其意义即在于此。

《考数根法》与《数根丛草》涉及的初等数论早期内容主要有下列各点:费尔马小定理，费尔马小定理的逆命题，纯循环小数的循环节长度与素数的关系，费尔马因数分解法，合数的最小素因子，威尔逊定理，平方剩余的概念等。以上内容在中国传统数学中并无研究基础。费尔马小定理的逆命题曾被认为成立。1819年，萨吕斯(F.Sarrus)举出反例，即2340≡1(mod 341)，但341=31×11，341不是素数。李善兰亦曾认为费尔马小定理的逆命题成立。［8］《考数根法》改正了这一错误，反例341亦出现在其中。华蘅芳、方士亦以该逆命题为真。此一现象中外颇为相似。《数根丛草》自序称，

该书光绪二十三年余经华序称，“去冬石印其《合数术》于沪”。以是知方士著有《合数术》一书。①华蘅芳、傅兰雅译《合数术》11卷(1887)，未刊，今传稿本，是书有林绍清节本《合数述》二卷，光绪十四年序刊，其内容源于Oliver Byrne，Dual Arithmetic:A New Art，London，1863。其内容与初等数论无关。对于探讨《考数根法》与《数根丛草》内容与方法之来源，是书当有重要意义。无奈迄今未见传本，不得其详。这一问题的研究有待新的史料发现。

参考文献

1 李善兰.考数根法［J］.中西闻见录.第2～4号，1872.

3 钱宝琮.中国数学史［M］.北京:科学出版社，1981.328～329.

4 严敦杰.中算家的素数论［J］.数学通报，1954(4):6～10;1954(5):12～15.

5 张祖贵.《数根丛草》研究［J］.自然科学史研究，1992，11(2).

6 Ore O.Number Theory and Its History［M］.New York:Dover Pub.Inc，1976.57 ～58.

7 闵嗣鹤，严士健.初等数论［M］.北京:高等教育出版社，1957.78.

8 韩琦.李善兰“中国定理”之由来及其反响［J］.自然科学史研究，1999，18(1).