解读崔锡鼎《九数略》中的九阶方阵

李国伟

(中研院数学研究所)

1 崔锡鼎与《九数略》

崔锡鼎(1645～1715)是活跃于朝鲜王朝肃宗时期(1674～1720)的文臣，根据《李朝实录》中肃宗四十一年(1715)记载:

癸卯，判中枢事崔锡鼎卒。锡鼎字汝和，号明谷，文忠公鸣吉之孙。清明恺悌，敏悟绝人。幼从南九万、朴世采学，刃解氷释，十二已通《易》，手画为图，世称神童。九经、百家，靡不通涉，如诵己言，既贵且老，犹诵读不辍，经术、文章、言论、风猷，为一代名流之宗。以至算数、字学，隐曲微密，皆不劳而得妙解，颇以经纶自期。十登台司，以破党论，收人才为心，以修明《大典》为事。辛巳三箚，受疾于己言人所难拔，赵泰采于枚卜，有大臣风。自在小官，上眷殊异，晩而不衰，党人甚忌之，始以毁经侮圣，诬之，终以侍疾不谨，构之，不得一日安于朝廷，处之晏如，终无几微见于色，人服其雅度。晩益栖屑，卒于荒野，识者恨之。然文胜且率尔，不能切深，论治似要而实泛，不若南九万之笃实精确焉。谥文贞，配享太庙庭。［1］

崔锡鼎的《九数略》［2］成书于肃宗十四年(1688)至肃宗二十一年(1695)之间，全书分4篇:

甲篇内容包括:数原、数名、数位、数象、数器、数法;

乙篇内容包括:统论四象、四象正数八法、四象变数八法;

丙篇内容包括:四象变数四法、九章名义、九章分配四象、四象分配九章、古今算学;

丁篇为附录，内容包括:文算、珠算、筹算、河洛变数。

对于《九数略》的总体评价，可用郭世荣的话作为代表:

总之，《九数略》是一本具有鲜明思想特点的数学著作，书中内容反映出作者崔锡鼎所掌握的数学知识相当丰富，对数学认识水平相当高，可以不夸张地说，和同时代的中国数学家水平不相上下，若是在中国，他也无疑是一位重要数学家。”［3］

本文关注的对象是《九数略》的附录“河洛变数”。在这篇附录里除河图与洛书两图之外，依照顺序还收集了四四图(及阴图)、五五图(及阴图)、六六图(及阴图)、衍数图(及阴图)、易数图(及阴图)、九数图(及阴图)、百子图、百子子数阴图、百子母数阴图、百子生成纯数图、百子生成交数图、百子阴阳子母错综图、天数用五图(即河图五五图)、地数用六图(即河图六五图)、河图四五图、河图七五图、河图八五图、河图九五图、洛书四九图、洛书五九图、洛书六九图、洛书七九图、洛书八九图(即五八井田图)、洛书九九图、范数用五图、重仪用六图、章策用七图、气策用八图、重象用九图、重卦用八图、候策用九图、九九母数变宫阳图、九九母数变宫阴图、九九子数变宫阳图、九九子数变宫阴图、天数用五图、洛书六觚图。

与宋朝杨辉《缉古摘奇算法》“纵横图”一章比较，除了聚六图外，崔锡鼎引录了所有其他各图。其中河图、洛书、四四图、五五图、六六图、衍数图、易数图、九数图、百子图名称均保留，并增补了杨辉未列的九九图阴图。此外，首幅天数五五图(即河图五五图)与杨辉的聚五图相同，第二幅天数五五图则是崔锡鼎自创。气策用八图即杨辉的聚八图、重象用九图即杨辉的攅九图、重卦用八图即杨辉的八阵图、候策用九图即杨辉的连环图。

以杨辉“纵横图”的内容来看，所谓纵横图的概念应该意指在规则的图形上标以连续正整数，使得在特定的区块里，标号的总和都是一个定数。西方所谓的幻方(或称魔方阵，magic square)便是一类特殊的纵横图。将自然数1，2，3，．．．，n2放入长宽均有n个格子的方阵里，使得每行、每列的和均为某一定数［不难算出此定数为n(n2+1)/2］，称为半幻方;如果两条主对角线的和也是同一定数，则称为幻方。虽然先前研究《九数略》的人，已注意到崔锡鼎自创的一些图形，例如孙成功说:“其中若干需要很高的构造技巧，具有组合学意义。”［4］但是整体上，似乎没有意识到他有超越杨辉纵横图的数学成果。孙成功的结论是:

《九数略》就数学内容来说，除了其构造的几个魔方阵之外，并没有超越作者所处的时代。《九数略》的典型意义在于它代表了“儒家明算者”对数学的认识和理解。例如崔氏的魔方阵研究跟中国、日本的游戏性研究不同，他研究河洛变数的目的主要在于借数的神秘性得到宇宙调和的法则，体现了象数神秘主义思想，这在某种程度上被认为阻碍了数学的发展。(［4］，28页)

其实“河洛变数”里的九阶方阵(方阵的阶数就是它的行数，也就是列数)暗藏了有趣的组合数学性质，这正是本文所准备剖析的焦点。在《九数略》甲篇的第六章“数法”，讲述了用筹算作加、减、乘、除的四法，从而绘出九九母数名图、九九母数象图(图1)、九九子数名图、九九子数象图(图2)。“河洛变数”里的九阶方阵都是从这些图变化而得。九九母数名图每一个小方格里，放了一个汉字的二位数。上面的位置(也就是十位数)称为纲数，可以看成表示方阵的列数。下面的位置(也就是个位数)称为目数，可以看成表示方阵的行数。①本文中“行”是指横行，“列”是指直列。为符合古汉文的排列习惯，从上向下计数方阵的行数，从右向左计数方阵的列数。请注意，现代矩阵符号使用法是从左向右计算列数。九九母数象图更可以理解为每个位置里放了左右两个数，左数为纲数，右数为目数，而不是每个位置放了一个二位数。这种理解九九母数图的观点，比较方便后面的一些有关方阵的结构分析。至于九九子数名图其实就是一张九九表，它的第m行与第n列的交叉方格里放的就是乘积mn。该图下方崔锡鼎的说明文字，已经明确地叙述了这些性质。

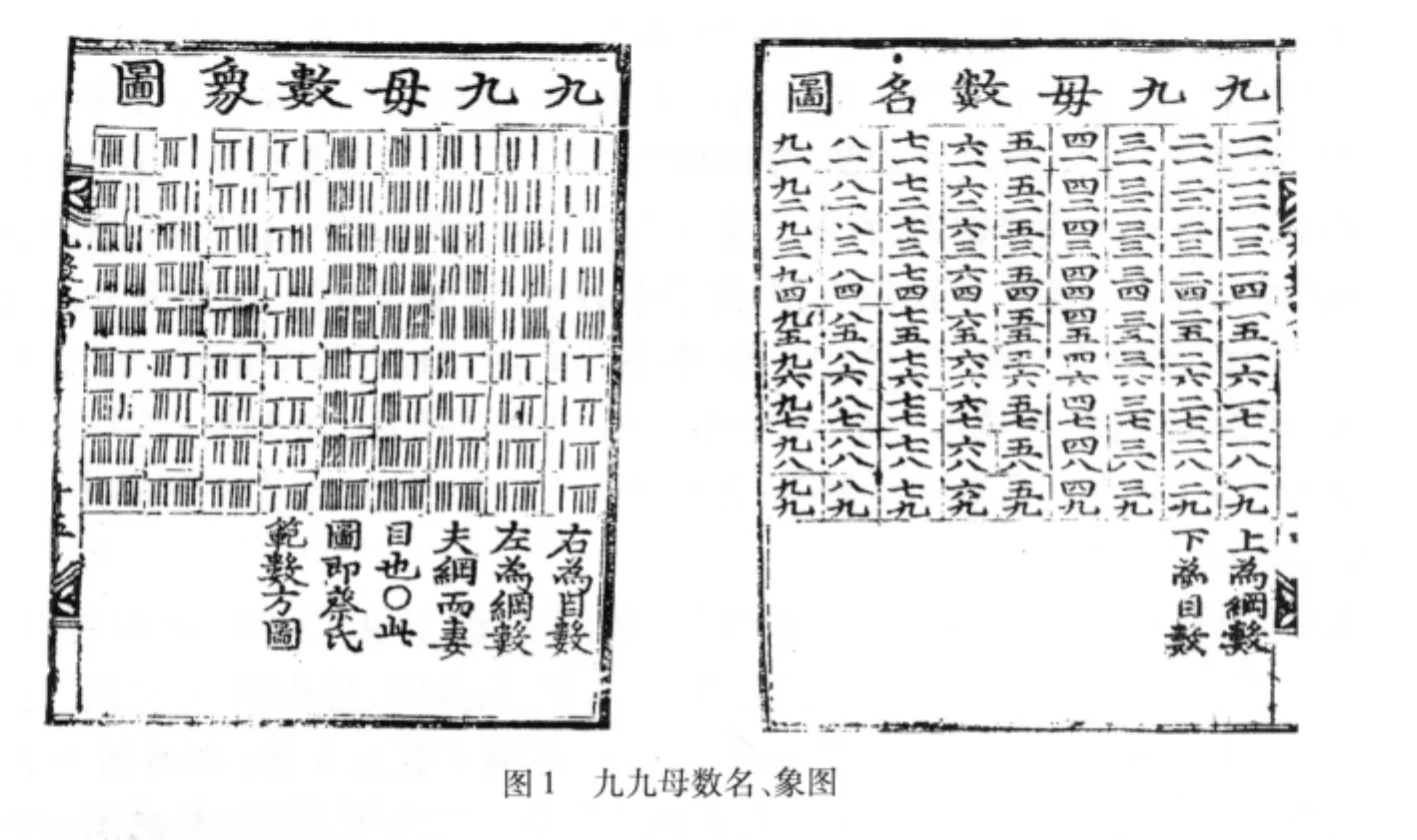
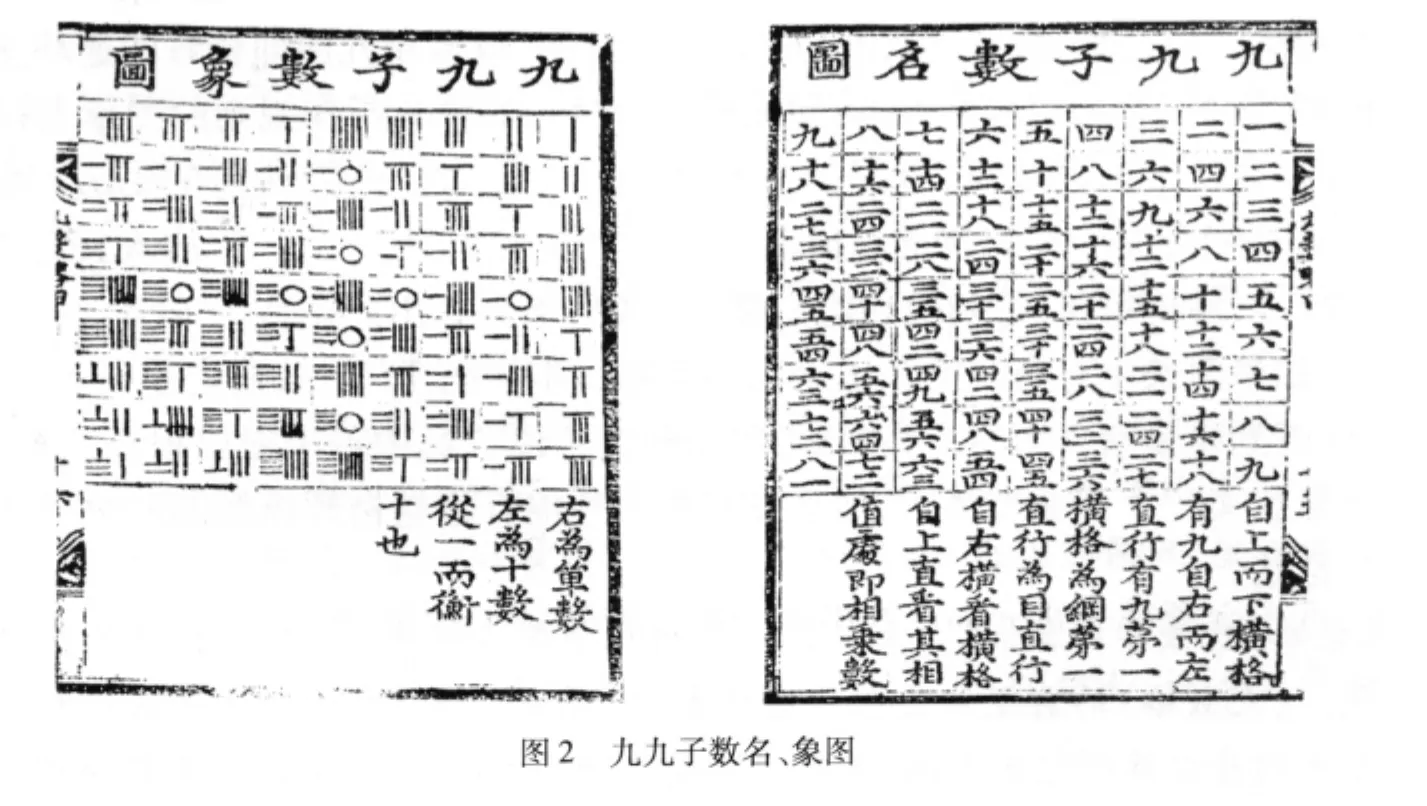
2 九九母数变宫阳图

“河洛变数”里的九阶方阵共有6种:九数图、九数阴图、九九母数变宫阳图、九九母数变宫阴图、九九子数变宫阳图、九九子数变宫阴图。其中以九九母数变宫阳图的数学内涵最为丰富，图3的左边是崔锡鼎的原图(最后一列跨页出现)，而右边是用现代数码表示出来的方阵，下文里称此方阵为M，而放在第i行第j列的元素记做mi，j。

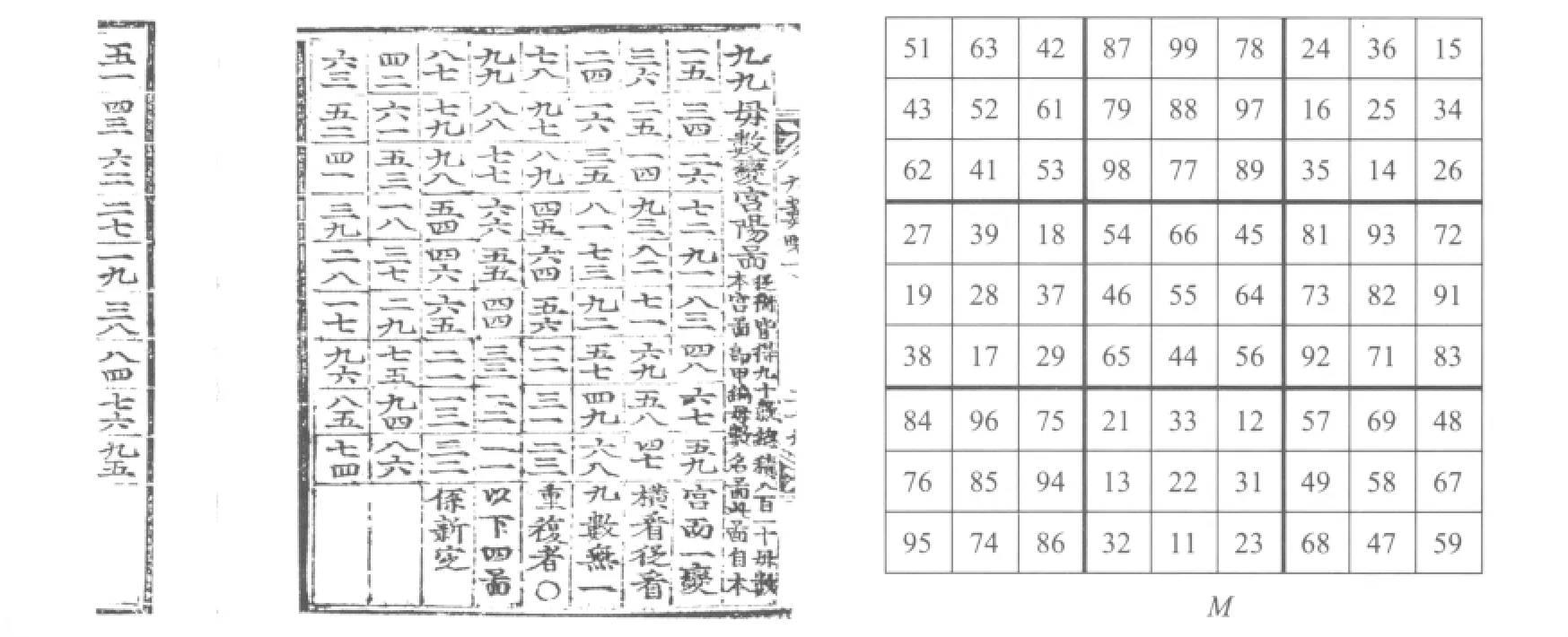
图3 九九母数变宫阳图与方阵M

崔锡鼎针对此图写的说明如下:

从衡皆得九十数，总积八百一十母数。本宫图即甲编母数名图，此图自本宫图而一变，横看从看九数无一重复者。

如果每个方格里的数字当作一个二位数来看，那么每一横行数字的总和并不是90。而且原来九九母数名图里就没有重复出现的数字，此处应不值得特别指出“横看从看九数无一重复者”。但是如果把每个二位数看成左右两个数码，那么每一横行(或每一直列)左边十位数的数码是从1到9，右边的个位数码也是从1到9，恰好“横看从看九数无一重复者”。1到9的总和是45，所以每行(或每列)18个数码总和恰为90，于是九行(或九列)中所有数码的总和就刚好是810。崔锡鼎观察到的“横看从看九数无一重复者”的性质，是一项中国古代纵横图制作中，未曾被人注意到的规律。这项规律符合西方数学所谓“拉丁方阵”(latin square)的特性。

拉丁方阵是一种特殊的n阶方阵，它的n2个位置恰由n种不同元素所占据，并且每种元素在每一行或每一列里都恰好出现一次。通常我们用数字1，2，3，…，n表示那n种不同的元素。西方最早有系统研究拉丁方阵的数学家是欧拉(Leonhard Euler，1707～1783)，他在1776发表了第一篇讨论拉丁方阵的短文De quadratismagicis(英译本On magic squares．http://arxiv．org/abs/math/0408230)，又在1782发表了篇幅甚长的Recherches sur une nouvelle espèce de quarrésmagiques(英译本 Investigations on a new type of magic square．http://eulerarchive．maa．org/docs/translations/E530．pdf)。欧拉引进并深入研究拉丁方阵的目的，在于利用拉丁方阵制造幻方。为了达成这项目地，他另外引入了“希腊拉丁方阵”(graeco-latin square)。一个n阶希腊拉丁方阵的每个位置上都放了一对元素，它们可区分为左元素与右元素。所有左元素构成的n阶方阵是一个拉丁方阵，所有右元素构成的n阶方阵也是一个拉丁方阵。最重要的条件是n2个位置里出现的元素对，没有两组是完全相同的［注意(a，b)与(b，a)是相异的元素对］。一般而言，任何两个拉丁方阵如果满足这个条件，就称它们是彼此正交的(orthogonal)。所以一个希腊拉丁方阵恰好可看成是两个正交拉丁方阵所迭合而成。为了纪念欧拉的重大贡献，希腊拉丁方阵也称为“欧拉方阵”。欧拉从一个n阶以数字构成的希腊拉丁方阵导出幻方的方法如下:首先把每一个数对(a，b)对应到正整数(a－1)n+b，这个对应在本文中称为“标准映射”。经过标准映射得到的方阵一定是半幻方，但并不必然产生幻方。如果原来的希腊拉丁方阵制作得够巧妙，使得两条主对角线经过标准映射后也达到定和，那才能造出幻方。

崔锡鼎的方阵M其实可以看成是一个欧拉方阵，它是由左数码构成的方阵L与右数码构成的方阵R迭合而成。图4绘出L与R，图5绘出标准映射把M对应到的幻方。

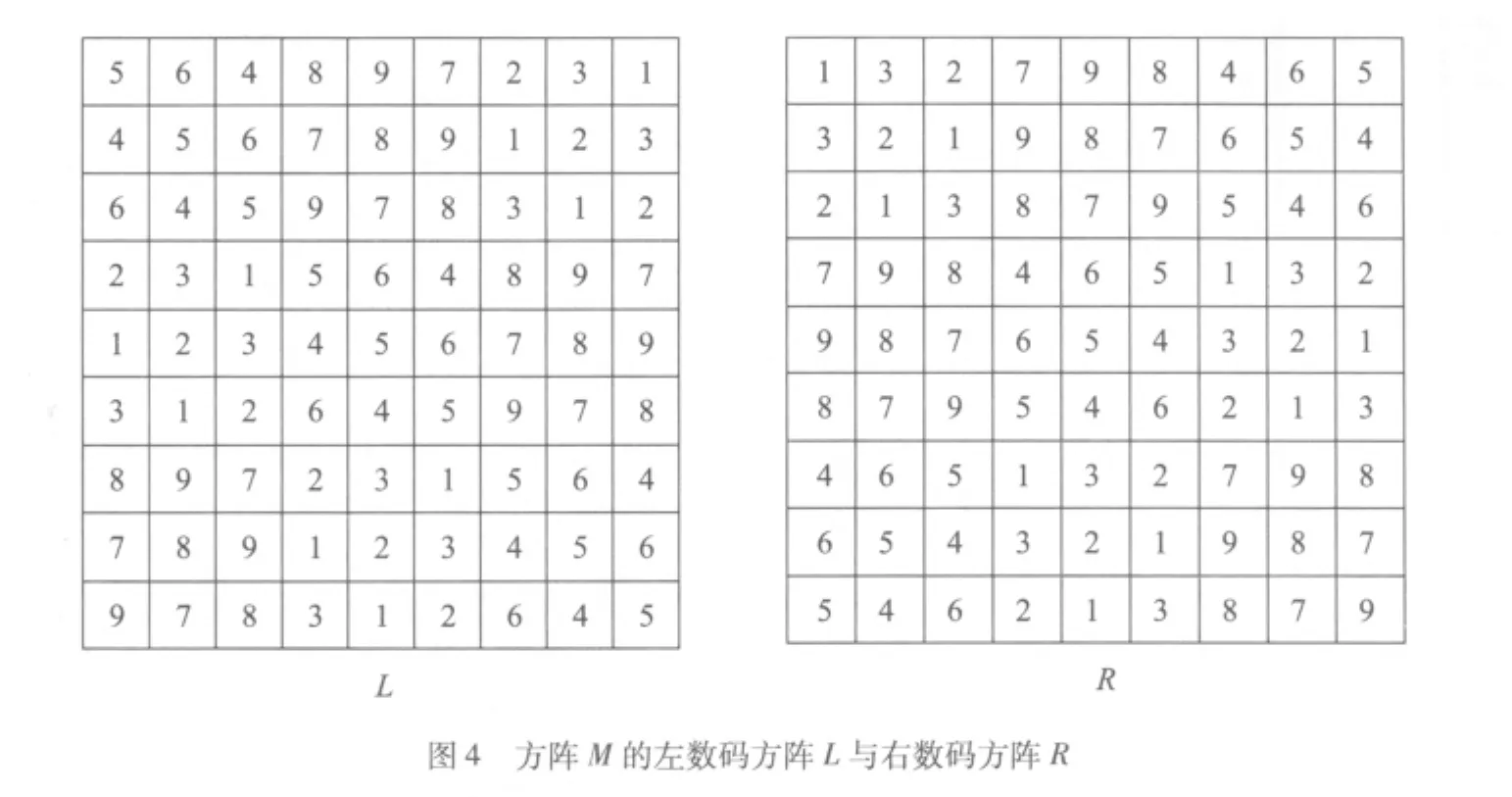
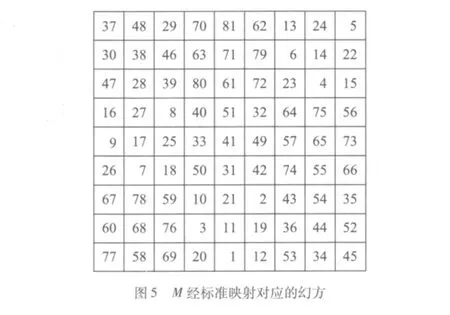
崔锡鼎在录用杨辉的纵横图时，当然理解幻方的规律，然而“河洛变数”通篇未明示可由九九母数变宫阳图，经过一定的程序得到幻方。韩国学者早在1993年便认为崔锡鼎通过正交拉丁方阵制作了九阶的幻方［5］，也注意到方阵M里每一横行的数字从左念到右跟从右念到左完全相同，也就是说每行都是回文(palindrome)，所以图4中L与R为对称的镜像［6］。其实比较平实的看法是这些都算是崔锡鼎方阵的现代解读。崔锡鼎也许未曾意识到自己创作的深层数学内涵，但是在韩国学者的解读之外，崔锡鼎的方阵还可挖掘出更多有趣的性质。

首先观察L与R的中心数字都是5，而且以中心点对称的两个位置上的数字总和均为10。所以回到M里，以中心点对称的两个位置上的数字总和均为110，包括中心数字55的两倍也是110。

其次，对于任何i(1 ≤i≤4)，假如同时把{mi，i，m10－i，10－i}，{mi，5，m10－i，5}，{m5，i，m5，10－i}，{mi，10－i，m10－i，i}这四组内的一对元素对调位置，就可得一个新的欧拉方阵(称之为Mi)，而且每个Mi可经由标准映射对应到一个幻方。图6以M1与M2为例，显示对角对边交换后的结果。

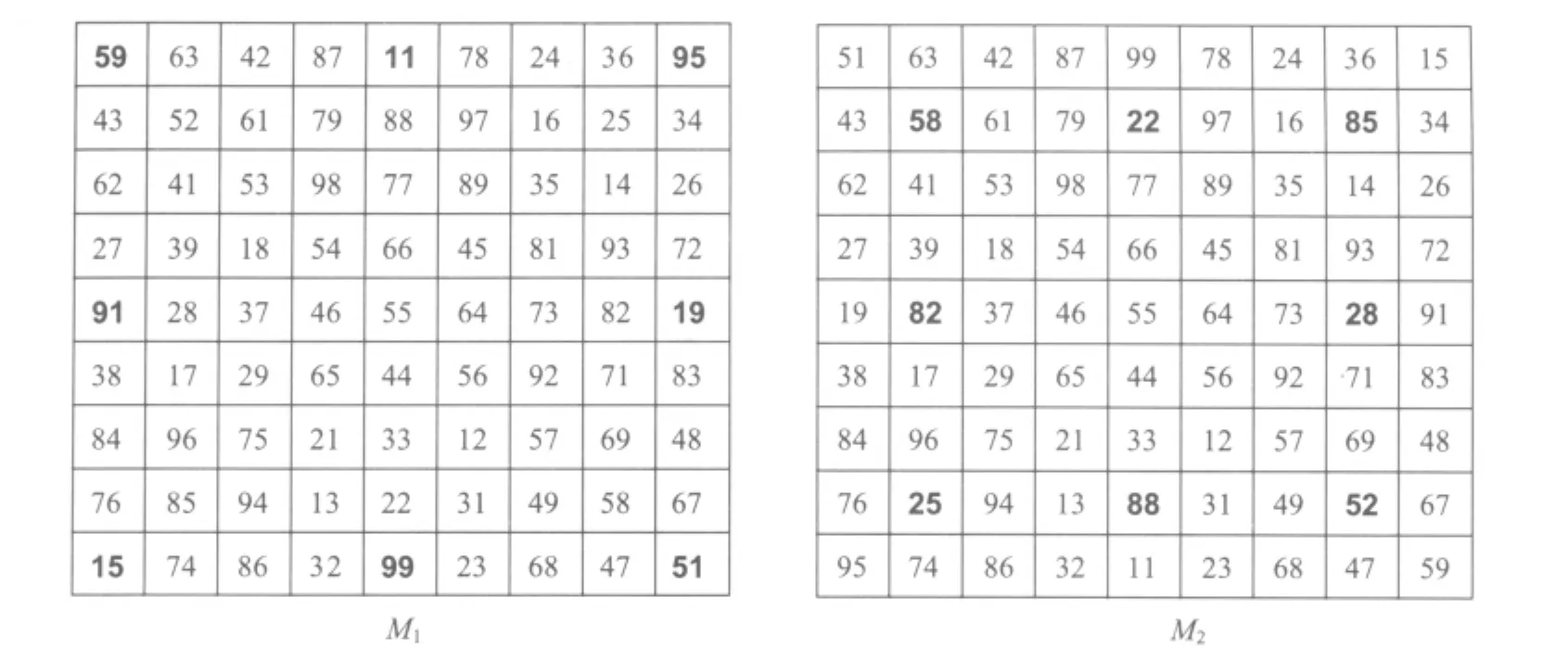
图6 M经对角对边交换后的M1与M2

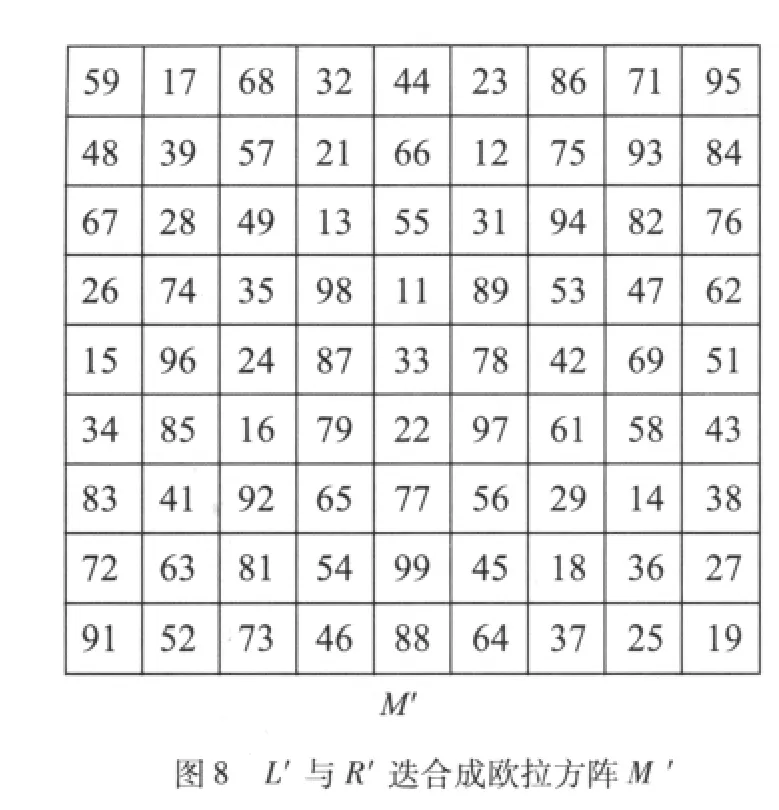
九九母数变宫阳图最出人意表的性质如下:把方阵M由上而下从正中剖开为左右两个方阵，也就是把第五列的各个元素的十位数归入左边方阵，而个位数归入右边方阵。左右方阵分别称为L'与R'(图7)，把它们迭合到一起，居然成为图8里的欧拉方阵M'，也就是说L'与R'是相互正交的拉丁方阵。M'没有M那么完美之处，是在标准映射之后，它并不能得到幻方。这种从正中剖开为左右两个正交拉丁方阵的性质，也适用于前一段所引进的方阵Mi(1≤i≤4)，它们同样不能在标准映射下得到幻方。

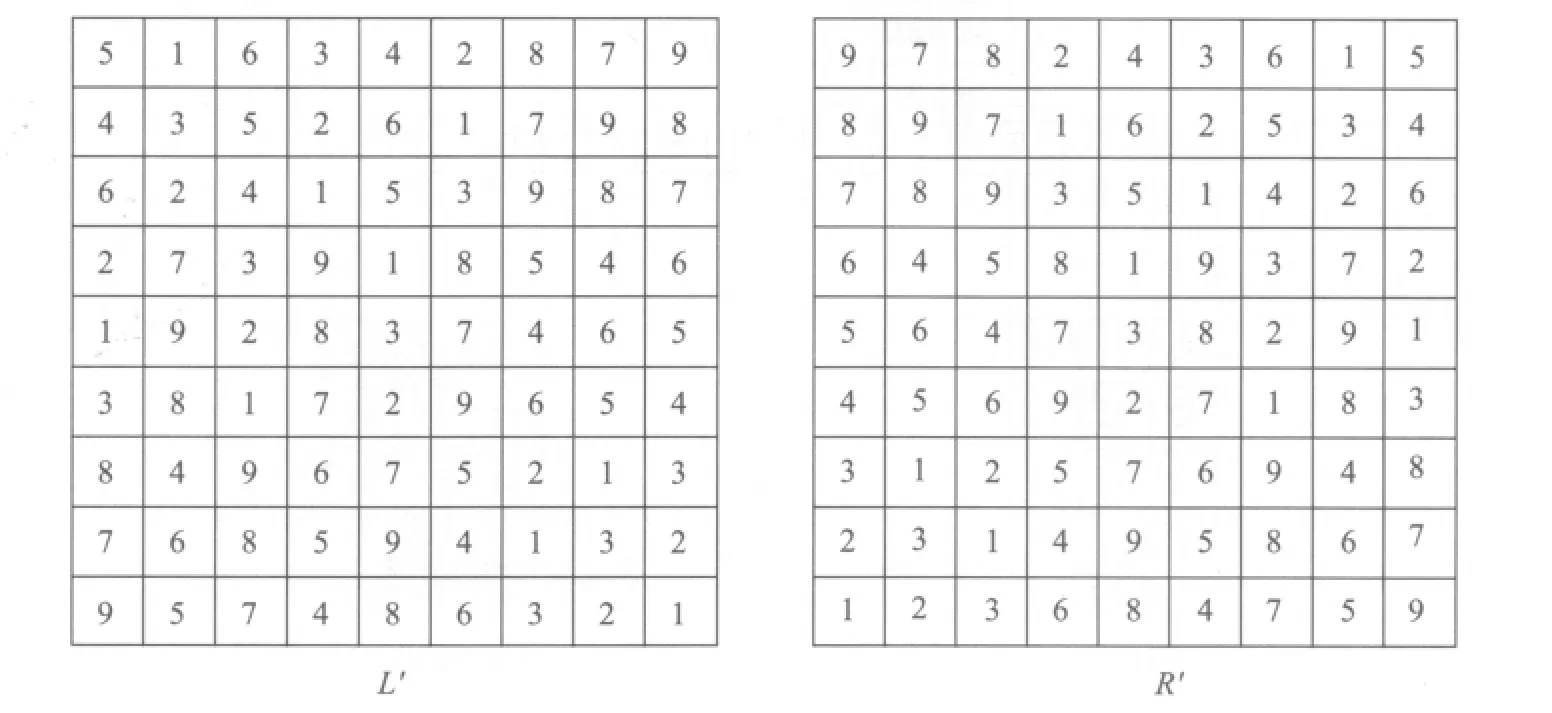
图7 把方阵M从正中剖开为左右两个方阵L'与R'

崔锡鼎在“河洛变数”里并没有说明如何造出九九母数变宫阳图。使用现代矩阵论的符号与观念，我们曾经提出一种以洛书为基础的构造法［7］。现在我们可以用更为符合洛书精神的方式来解释M的构造法。图9左边是1到9按照从上到下由右至左的排列，右边的洛书可看成是左边按照数字的大小依箭头顺序排出。这个顺序在道士步罡踏斗时称为“禹步”［8］，在纵横图的研究上有称之为“洛书范型”［9］，本文中就称之为“洛书顺序”。

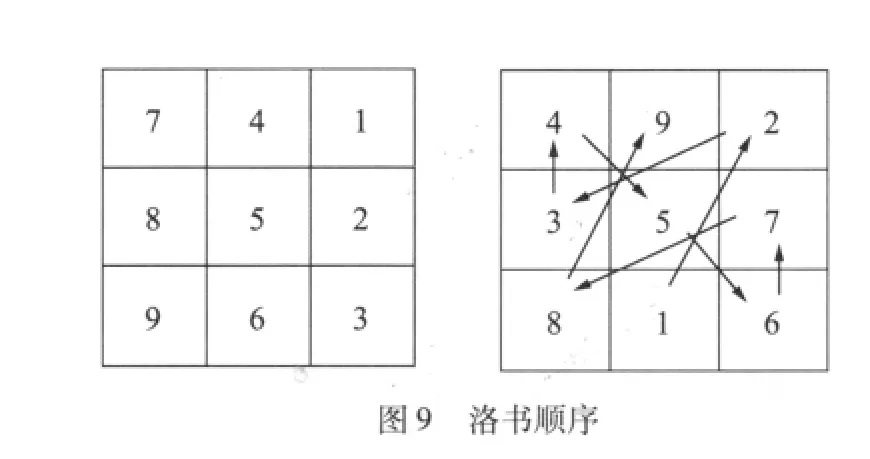
图1右边的九九母数方阵可以划分成九宫，使得每宫里是一个九阶小方阵。然后把这些小方阵按照洛书顺序排列，图10左边只显示出头三个小九阶方阵在洛书顺序下所占的位置。之后，把每个九阶小方阵再按洛书顺序排列它的九个元素，就会得到方阵M，图10右边也只显示左边三个小方阵的排列结果。我们称这种构造的方法为“整块双重洛书顺序移动法”，简称“块洛书法”。利用块洛书法虽然很快造出九九母数变宫阳图，但是用矩阵方法却顺便可证明新观察出来方阵M所满足的一些特性。①Swetz在(［10］，图7．25)中使用“块洛书法”造出本文图5的幻方，不过Swetz对于崔锡鼎的工作并无所悉。

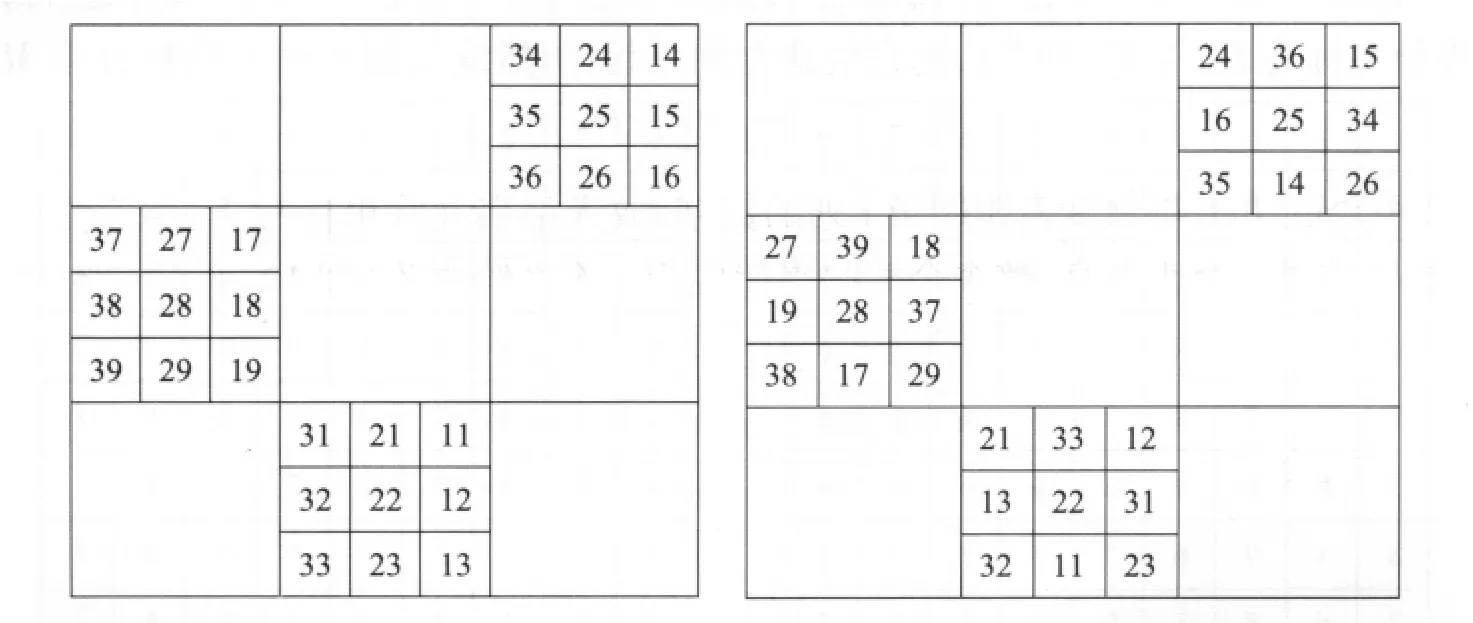
图10 部分显示整块双重洛书顺序移动法的两个步骤

3 九九母数变宫阴图

在九九母数变宫阳图之后，崔锡鼎紧接着给出九九母图变宫阴图(图11左图)。他的说明是:

共积上同。从衡及九宫皆得九十数。九宫之内，每行三子皆得三十数。阳图则九宫数多少不齐，此图视阳图尤妙，允符洛书之数。

我们首先注意到，如果把九九母数变宫阴图的十位数与个位数分别放入九阶方阵，两个方阵都没有满足拉丁方阵的要求。而且此图经过标准映射后，并不会得到幻方。九九母数变宫阴图可以画为九宫，每宫内每行六个数码和是30。九九母数变宫阳图第i行的数字，都出现在图11右图所示九宫的标号i位置。图11右图其实是在洛书里，以中心对称的各对数字交换所得。除了第3、7、9宫外，其他各宫依数字大小走出的顺序，若不是洛书顺序，就是洛书顺序左右交换后的顺序。上述总和30之数，恰为洛书每行总和15的倍数，崔锡鼎也许因而认为“此图视阳图尤妙，允符洛书之数。”崔锡鼎在建造这个九阶方阵时，没有严谨地遵守洛书顺序，也许因此他错失了原本可以更好的构造。

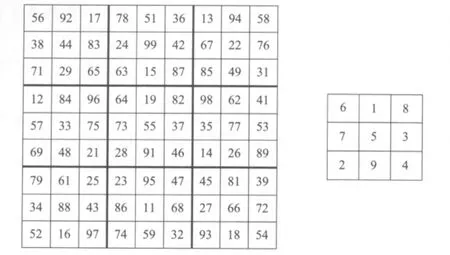
图11 九九母图变宫阴图

假如我们把九九母数变宫阳图第i列的数字，放入洛书九宫里标号i的位置，并且再按洛书顺序排成一个小九宫，整个合并起来就成为一个九阶方阵(图12)。我们称这种构造的方法为“整列双重洛书顺序移动法”，简称“列洛书法”。每个小九宫里的三阶方阵，它的每行、每列、两主对角在线的数码和都是30。我们造的这个改良的九九母数变宫阴图，经过标准映射之后会得到幻方。崔锡鼎没有作出这个性质更好的方阵，一个可能是他并没有系统地应用双重洛书顺序法，另一个可能是他并没有从九九母数变宫阳图体会出所对应的幻方，所以他在作阴图时也就没有计较所得的方阵能否变换成幻方了。

假如我们拿九九母数变宫阳图的各行仿照上法去作，也会得到一个九阶方阵。我们称这种构造的方法为“整行双重洛书顺序移动法”，简称“行洛书法”。构造出的九宫中，各小方阵的诸行诸列数码和也是30，但是对角在线的数码和不尽然是30。这个九阶方阵在标准映射下仍然会得到幻方。

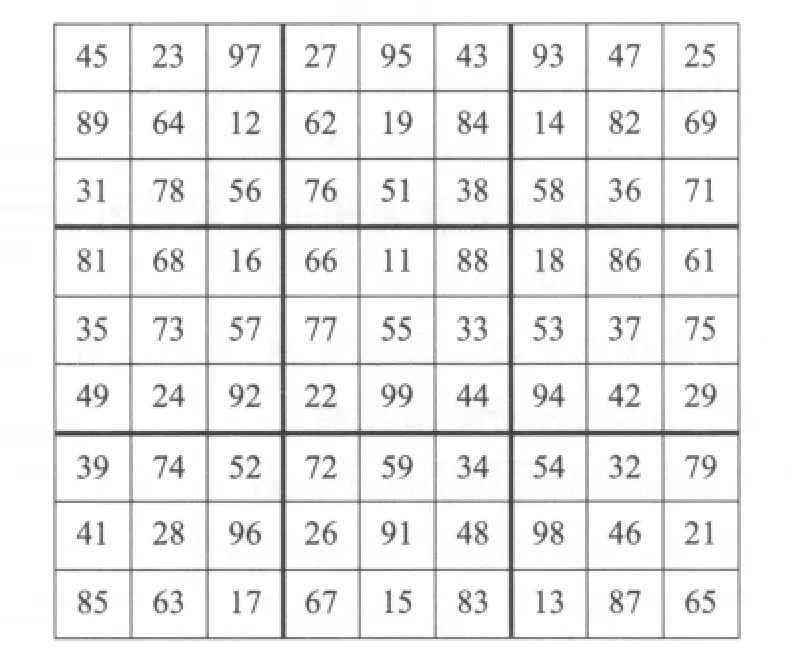
图12 改良的九九母数变宫阴图

4 九九子数变宫阳图与阴图

在九九母数变宫阴图之后，就是九九子数变宫阳图(图13)。此图是从九九子数图(图2)按照行(或列)洛书法得来，因此划分为九宫之后，每个小宫都是洛书的倍数。依崔锡鼎的话来说:

从衡二百二十五。共积二千二十五，经纬错综之妙不可其述。此图分为九宫，即是洛

书之数。

从这样的造法可推论出九九子数变宫阳图是一个广义幻方，也就是它的每行、每列、两主对角在线数字的和都相等。本来九九子数图是一个乘法表，经过这种变换后，成为一个满足加法上定和性质的广义幻方，像这种连结乘法性质与加法性质的构型，在古代数学里十分罕见，因而也特别有趣。

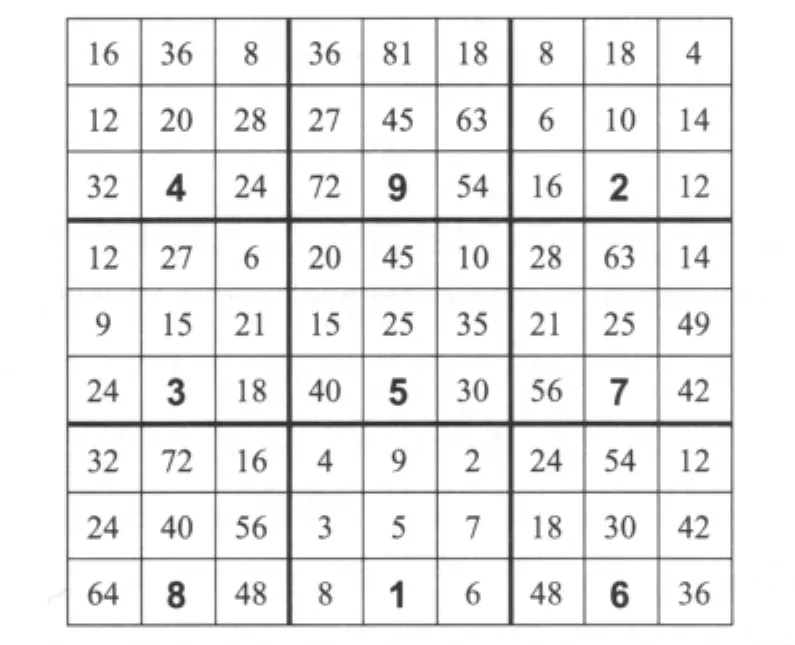
图13 九九子数变宫阳图

紧接着九九子数变宫阳图是九九子数变宫阴图(图14)。此图如果以右上到左下的对角线作为轴线，则方阵的上左半与下右半是对称的。此图也是一个半幻方，每行每列的数字和都是225。崔锡鼎对此图说明如下:共积上同。从衡皆得二百二十五数。右四图九九变数以上即倍加通乘之数。此图即自本宫而一变者，自一至八十一为脊，左右分排，井井不紊。

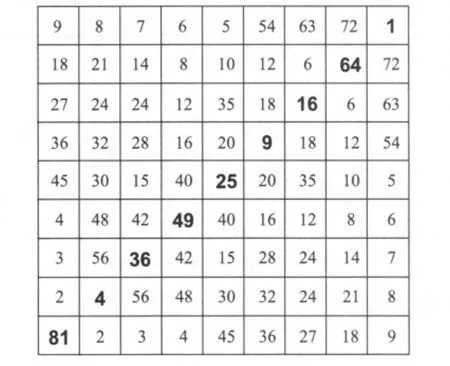
图14 九九子数变宫阴图

因为在九九子数图中，如果i≠j，则ij与ji各出现一次，所以在满足对称的要求下，只有完全平方数会出现在右上到左下的对角在线。1到81共有九个完全平方数，不过它们并没有按顺序由小排到大。其实九九子数变宫阴图的行与列加以重排，可以得到图15里更加整齐的形式，使得所有完全平方数都依顺序出现在对角在线。崔锡鼎是依照什么样的法则构造出九九子数变宫阴图，仍有待研究。

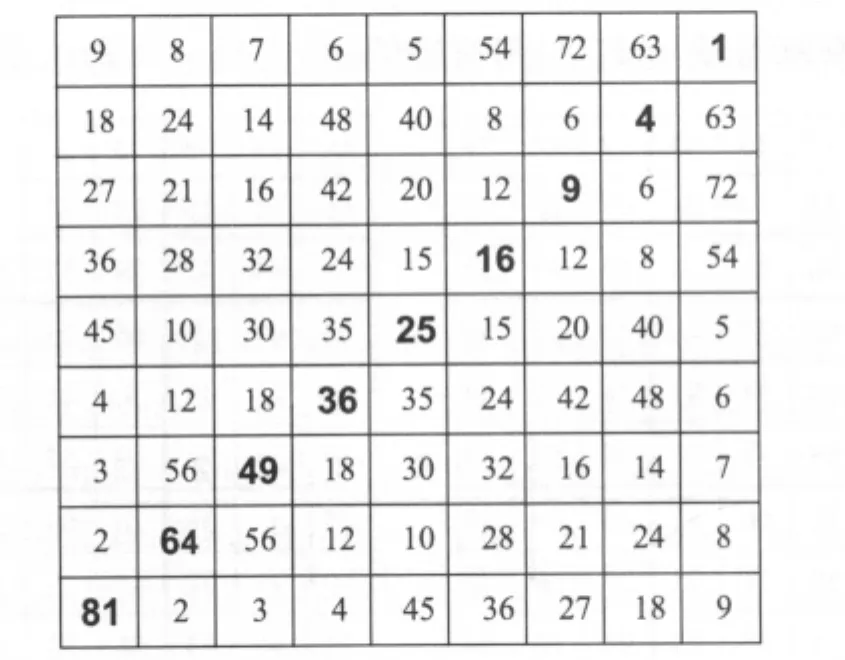
图15 重排的九九子数变宫阴图

5 九数图及其阴图

崔锡鼎在“河洛变数”里的九数图(图16右图)，就是杨辉《缉古摘奇算法》“纵横图”里的九数图。它不仅本身是一个幻方，它的九宫也都是广义幻方。九数图的作法可由图16左图出发，然后用行洛书法就能完成。我们也可以从图1的九九母数图出发，用行洛书法得出一个方阵，然后施以标准映射，结果同样是九数图。

图16 用行洛书法可将左图转换为右方九数图

崔锡鼎的九数阴图(图17右图，崔锡鼎原图中5与37应对调)是另外一个幻方，他说:

从衡三百六十九数。分为九宫，每宫亦得右数。每宫一行三子各得一百二十三，从衡皆然，此非九九合数，乃一至八十一数。杨辉有阳图而无阴图，故新定，此图条理齐整，视辉尤妙。

不仅每行每列与两条主对角在线数字和为369，每小宫均为半幻方，而每小宫里九个数字和也刚好是369，因此崔锡鼎自认此图的巧妙更胜过杨辉的九数图。崔锡鼎并没有讲他如何得到这个更高明的图，但是如果我们把此图当作是某个方阵经过标准映射得来，也就是把标准映射的逆映射作用在此图上，便可得到图17左图。此图与九九母数变宫阴图相当类似，它的每个小宫都可从图11左图对应的小宫，经过对称或旋转得到。

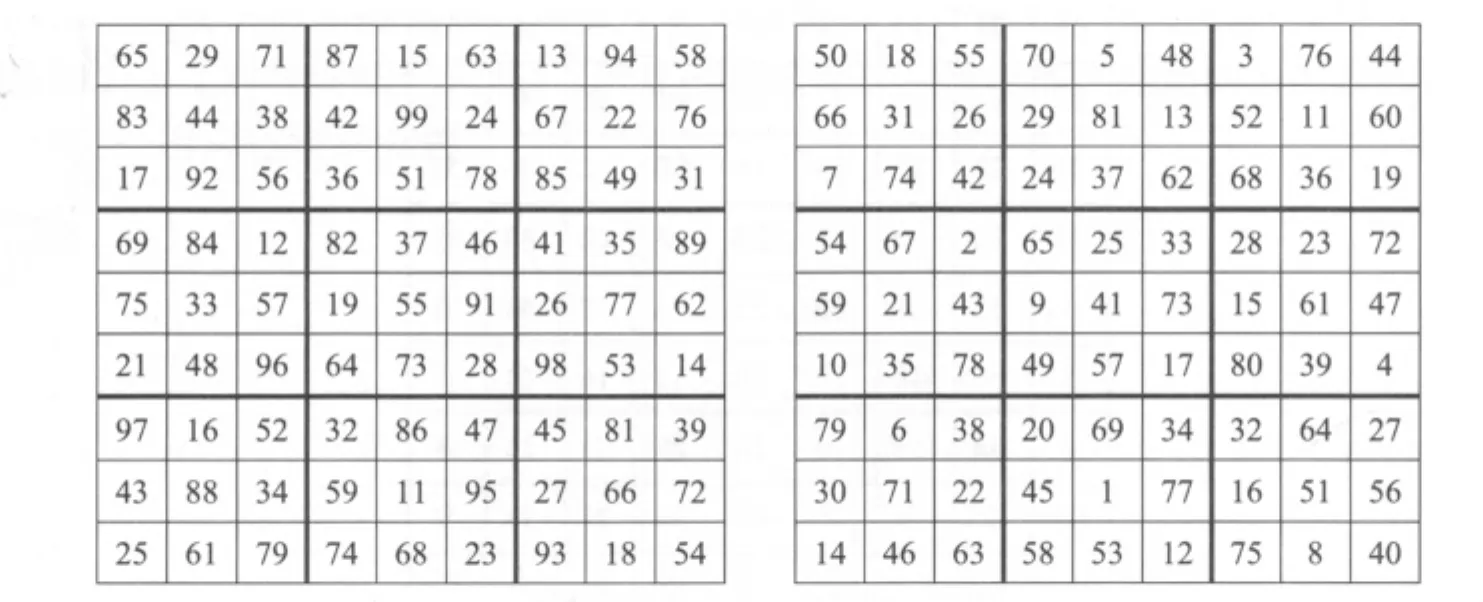
图17 左图经标准映射得右方九数阴图

6 结语

从以上的解读里，我们可以看出崔锡鼎“河洛变数”里的各种方阵，以九阶中除九数图之外的各图最有原创性，也蕴藏了最丰富的数学内涵。也许崔锡鼎本人并未理解到这些较深刻的意义，但是在我们适当的解读后，甚至可以促进发展新的问题与新的研究。例如:(1)除了九九变宫阳图外，一般而言有哪些奇数阶欧拉方阵可以从正中剖开，分成左右两个相互正交的拉丁方阵?(2)尝试把九九子数阴图推广到一般的n阶乘法表，也就是说给定一个n阶方阵，它的第一行与第一列依序放入1，2，…，n，而方阵的(i，j)位置放入乘积ij，这样一个n阶乘法表可否加以重新排列，使得排列后以主对角线对称，并且每行每列数字的和都是定数?这是一个很有意思的“古为今用”的组合数学问题，之前似乎未见有人提出。①当n=4k+2的形式时，这种方阵是不存在的。当n是4的整倍数时，李渭天证明这种方阵肯定存在。并且在不要求以主对角线为对称的情形下，甚至可造出广义幻方。当n=5，7，8时，李国伟、李渭天、刘德芬都构造出这种方阵，而且主对角在线的数字是依序排列。至于在最一般的情形下，此问题尚未完全解决。

1 肃宗实录补阙正误．41年(1715年)11月11日．卷56［DB/OL］．［2011-10-23］．http://sillok．history．go．kr/inspection/inspection．jsp?mTree=0＆id=ksb．

2 崔锡鼎．九数略［M］//金容云．韩国科学技术史资料大系．第1册．汉城:骊江出版社，1985．

3 郭世荣．中国数学典籍在朝鲜半岛的流传与影响［M］．济南:山东教育出版社，2009．35．

4 孙成功．朝鲜数学的儒学化倾向——《九数略》研究［D］．天津:天津师范大学，2003．23．

5 Hahn SG，Oh Y Y．Choi Seok-Jeong and hismagic squares［J］．Journal of KSESM，1993，(32):205～219．

6 Song H Y．Choi'sorthogonal latin squares isat least67yearsearlier than Euler's［OL］．［2009-2-6］．http://coding．yonsei．ac．kr．

7 Lih KW．A remarkable Euler square before Euler［J］．Mathematics Magazine，2010，(83):163 ～167．

8 Anderson P．The practice of Bugang［J］．Cahiers d'Extrême-Asie，1989，(5):15 ～53．

9 侯刚，刘钝．宋代的洛书纵横图［R］//前现代与非西方科学技术之视觉表现国际学术研讨会(2009年12月13日)．新竹:台湾清华大学，2009．

10 Swetz F J．Legacy of the Luoshu:The4，000yearssearch for themeaning of themagic squareof order three［M］．Wellesley:A．K．Peters．2008．