拉丁方秘密共享方案

李 国，殷俊锋，李 静

(中国民航大学 计算机科学与技术学院，天津 300300)

0 引 言

“秘密共享”[1,2]描述了将秘密信息S进行分割，分割后的部分信息称为一个共享“share”。将share分发给具有保密权限的人员(称为“参与者”)，每个参与者持有其中的一个share分片，即秘密信息的一部分。部分参与者将持有的share分片结合起来，就能恢复秘密信息S。

拉丁方的数学结构[3]也被用来探究建立秘密共享方案的模型，构建了基于拉丁方特性的秘密共享方案[4-6]。基于拉丁方“临界集”[7]的秘密共享方案通过分发“临界集”来实现秘密共享，但找到一个阶数n较大的拉丁方临界集是非常困难的，这使得基于拉丁方临界集的秘密共享方案初始化和重构难以实现。此外用于秘密共享的拉丁方临界集直接暴露也使得该类型的秘密共享方案存在缺陷。

针对早前一系列拉丁方秘密共享方案存在的问题，本文提出了一种拉丁方秘密共享方案。该方案利用拉丁方“轮廓与合适的自合痕”可唯一恢复该拉丁方的特性，将随机生成的部分拉丁方与特殊自合痕构造的拉丁方经过合痕转换后作为“秘密”，从该秘密拉丁方中随机选择“轮廓”，经过合痕转换后构造门限方案进行秘密共享。对于秘密的重构则需收集一定数量的share分片来进行秘密拉丁方的恢复。本方案初始化阶段简单易操作，在秘密拉丁方的重构阶段也简化了不必要的步骤，同时引入了秘密分片的保护措施，提高了秘密共享的安全性。此外还在秘密共享方案的容错性和秘密共享的多级方案等方面有所提高。

1 相关知识

1.1 拉丁方

(1)由正整数和0组成的n行n列的方阵，在这个方阵里，恰有n种不同的元素，每一种不同的元素在同一行或同一列里只出现一次。用i,j∈{0,1,2,…,n-1}且n>1分别表示元素k在第i行，第j列的索引。则方阵中任意一个元素k可以用三元组(i,j∶k)来表示。

如图1所示，左侧拉丁阵第2行第1列的元素2可以表示为(2,1∶2)。当i,j∈{1,2,…,n}且n>2时，右侧拉丁阵第2行第2列的元素3可以使用(2,2∶3)来表示。

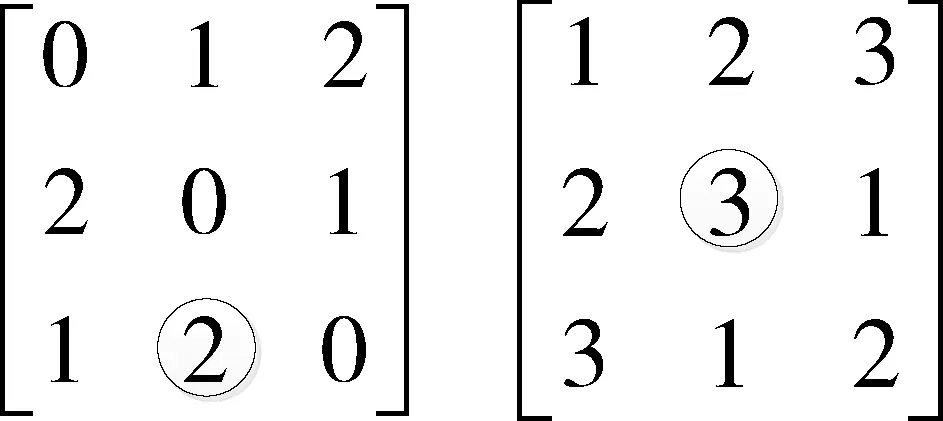
图1 3阶拉丁方

(2)部分拉丁方：设N是n个不同元素的集合，P是一个n阶方阵，若N中的每一个元素在P中只出现一次，则称P是定义在N上的一个部分n阶拉丁方，P中有些位置可以为“空”[8]。图2是在不同位置元素为空的部分3阶拉丁方。

图2 部分3阶拉丁方

1.2 合痕与自合痕

含有n个元素的有限群A的全体置换做成的群，叫作n次对称群，通常记为Sn。令In=Sn×Sn×Sn，其中Sn是作用于[n]的n次对称群[9]。对于每一个映射θ=(α,β,γ)∈In。令三元组(i，j∶k)表示拉丁方L中i行，j列的元素k。当三元组通过α交换行的索引，β交换列的索引，γ交换元素符号后得到一个新的拉丁方θ(L)，即：θ(L)=θ((i’,j’∶k’))=(α(i),β(j)∶γ(k))，i，j∈Zn。

则这种映射θ被称为合痕，经过合痕转换后的拉丁方θ(L)与拉丁方L是合痕的。而拉丁方L经过映射θ转换后得到的所有同阶拉丁方称为L的合痕类[10]。

如果θ=(α,β,γ)∈In满足θ(L)=L，即拉丁方L经过合痕转换得到该拉丁方L本身，则这种特殊的合痕θ是拉丁方L的一个自合痕，即：L(i，j∶k)=θ(L)=θ((i’，j’∶k’))=(α(i),β(j)∶γ(k))，i，j∈Zn。

1.3 轮 廓

在拉丁方L中挑选部分三元组集合构成一个部分拉丁方P，在一个合适的自合痕θ作用下经过循环置换可以重构拉丁方L，则称这个部分拉丁方P为“轮廓”，使用“C”来表示[11]。

算法1： 轮廓C与合适的自合痕θ生成拉丁方L。

输入： 轮廓C， 自合痕θ

输出： 拉丁方L

(1)L ← n×n arrays

(2) for i← 0 to n-1

(3) for j← 0 to n-1

(4) if(C[i][j]≠null)

(5) for k∈{0,1,…,n-1}

(6) L[i][j]←θk(C[i][j])

(7) endfor

(8) endif

(9) endfor

(10) endfor

(11) return L

例如：当自合痕θ=((012),(012),(012))的时候，使用算法1从轮廓C经过循环置换可以得到拉丁方阵L。图3是(C,θ)生成拉丁方L的具体过程[12]。

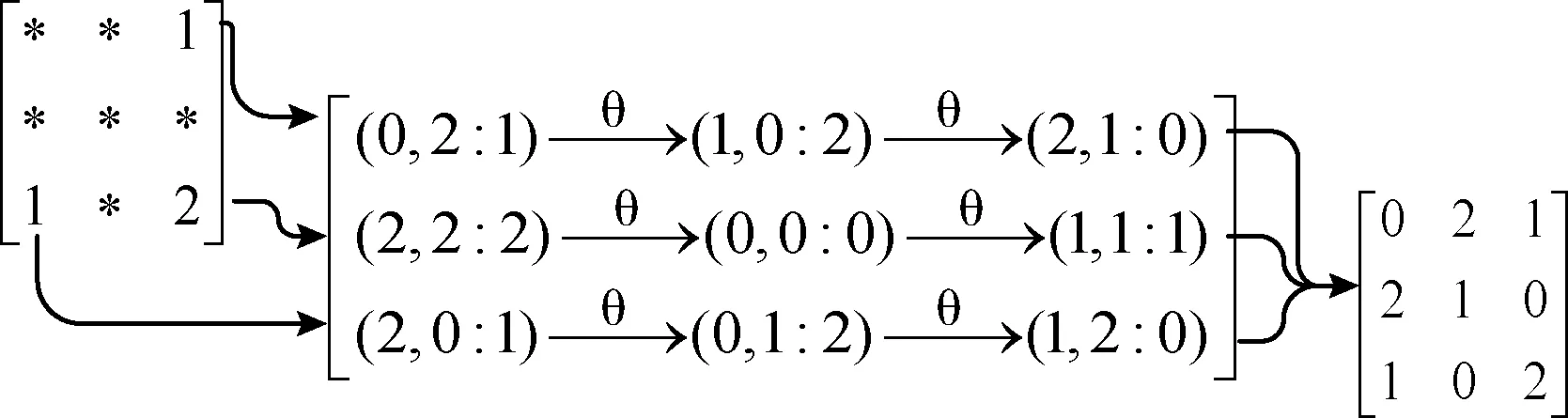
图3 轮廓C与合适的自合痕θ生成拉丁方L

2 拉丁方秘密共享方案

2.1 方案初始化步骤

利用拉丁方“轮廓与合适的自合痕”可唯一恢复该拉丁方的特性，将随机生成的部分拉丁方P与特殊自合痕ξ构造的先导拉丁方Lpre经过合痕转换后生成的拉丁方L作为“秘密S”，从该秘密拉丁方L中选择部分三元组得到轮廓C与合适的自合痕θ，随后将经过合痕转换后的C’中的三元组集合进行随机分割，得到的碎片称为“share”。由唯一具有分发授权的参与者将share分片随机分发给其它N个参与者δ1,δ2,…,δN。 δ持有的部分信息作为秘密拉丁方的共享“share”。该拉丁方秘密共享方案主要有以下4步：

步骤1 在特殊自合痕ξ下生成先导拉丁方Lpre。随机构造一个n阶部分拉丁方P。令i∈{0，1，…，n/2-1}，随机选择ki∈{0，n/2}。得到P的三元组集合A[12]，即：A={(n/2-1-i,i∶ki)，(n-1-i，n/2+i∶ki)，(n-1-i,i∶n/2-ki)，(n/2-1-i，n/2+i∶n/2-ki).}以n=6为例，从三元组集合A中得到部分拉丁方P

令特殊自合痕ξ=(τ,τ,τ)，τ=(0,1,…,n/2-1)(n/2,n/2+1,…,n-1)。定理1和算法1保证了(P,ξ)生成拉丁方Lpre。当n=6时，ξ=((012)(345),(012)(345),(012)(345))，部分拉丁方P与特殊自合痕ξ可以得到秘密拉丁方L的先导拉丁方Lpre

定理1 令D=(di,j)是一个部分n阶拉丁方阵，其中包含2n个已经定义的元素，每个元素都属于{0，n/2}。当且仅当：

(1)每个块M11、M12、M21和M22都精确地包含n/2个元素；

(2)如果(i,j,di,j)和(i’,j’,d’i,j)是一个块中的两个不同的项，那么j-j’≡i-i’(mod n/2)

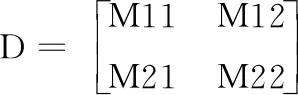
然后，(D,ξ)生成一个拉丁方。(特别注意的是定理1必须保证在n≡2(mod4)情况下成立。)

证明：这是一个定理的特殊情况[13]。

步骤2 随机生成秘密拉丁方L与自合痕θ；

随机生成一个合痕Φ，令L=Φ(Lpre)，将拉丁方L作为秘密S。根据引理1可知：由Lpre的特殊自合痕ξ=(τ,τ,τ)与合痕Φ进行运算，可以得到L=Φ(Lpre)的自合痕θ=ΦξΦ-1。例如：随机生成Φ=((15234),(134),(1243))，则秘密拉丁方L

由引理1可知，Lpre的特殊自合痕ξ与合痕Φ和Φ-1经过循环置换得到L=Φ(Lpre)的自合痕θ=ΦξΦ-1=((053)(124),(032)(154),(024)(135))。

引理1令λ∈S3。令θ、Φ∈In，并且L是一个n阶拉丁方。然后：

(1)当且仅当ΦξΦ-1∈Atp(Φ(L))时，θ∈Atp(L)；

(2)当且仅当θλ∈Atp(Lλ)时，θ∈Atp(L)。

引理1的证明在文献[14]。

步骤3 利用秘密拉丁方L的轮廓C得到C’；

在拉丁方L中选择m∈(n2/3≤m≤n2/2且N取整数)个三元组得到轮廓C，再随机生成合痕Φ’，令C’=Φ’(C)。利用C’包含的三元组构造(K，N)门限秘密共享方案。

例如在L中挑选15个三元组组成轮廓C，随机生成合痕Φ’=((145),(14352),(1423))

将轮廓C包含的三元组在合痕Φ’下进行合痕转换得到C’

由于轮廓C是秘密拉丁方L的一部分，将C直接分发给参与者后每个参与者就得到了秘密拉丁方L的一部分信息，相当于直接暴露了秘密S的一部分，一个不怀好意的攻击者极有可能利用这些裸露的share分片进行攻击从而得到整个秘密拉丁方L。为了避免这一情况的发生，进行上述操作，经过合痕转换后的C’不包含秘密拉丁方L的任何信息，避免了在之前的拉丁方秘密共享方案中share分片等重要信息的直接暴露，增加了秘密拉丁方L的安全性，防止部分秘密分片的泄露危害整个秘密的安全，进而保证了秘密S的足够安全。

步骤4 将C’进行随机分发；

根据(K,N)门限秘密共享方案[15]的要求由具有安全权限的分发者将C’随机分发给N个参与者(K值可以根据实际情况的要求进行随机选择)，得到δ1-δN的三元组集合，每个参与者得到的share分片所包含的信息量是相同的。

例如在K=4，N=5时构造(4，5)门限秘密共享方案，将C’分为5份：δ1-δ5，每个δ中包含了3个三元组集合，每一份的详细构造如下

δ1=((0，0∶5)，(3，0∶0)，(4，2∶2)), δ2=((1，0∶3)，(3，3∶4)，(2，5∶5)), δ3=((1，3∶1)，(4，5∶0)，(2，4∶2)), δ4=((1，4∶0)，(4，1∶5)，(2，2∶1)), δ5=((5，4∶3)，(0，3∶2)，(5，1∶4)).

在早期的拉丁方秘密共享方案中，含有秘密的share分片不能丢失，不能损毁，缺少任何一个share分片就不能进行秘密的恢复。基于此，本文中在秘密分发过程中利用门限秘密共享方案增加了早前拉丁方秘密共享方案所没有的“容错性”，K个或者多于K个share分片结合在一起就能够恢复秘密拉丁方L。因此本方案可以容忍一定数量的share分片丢失或损毁，剩余的share分片同样能够恢复秘密拉丁方L。

对于前文构造的(4，5)门限秘密共享方案来说：任意得到δ1-δ5中的4个share分片，就可以利用本文中的拉丁方秘密共享方案的恢复过程解得秘密拉丁方L，进而得到秘密S。该拉丁方秘密共享方案的“容错性”极大减少了秘密丢失的风险，有力提高了秘密保护的安全性。

经过拉丁方秘密共享方案的初始化步骤后，每个参与者可以得到C’的一部分信息share分片，自合痕θ与合痕Φ’是公开的。但这种公开是有条件的，为了秘密的足够安全，不会把θ与Φ’公开给所有人，只会将它们公开给具有权限的参与者。换句话说，本方案选择将θ、Φ’与C’一起分发给参与者。图4描述了该拉丁方秘密共享方案的初始化流程。(PRNG是伪随机数发生器)。

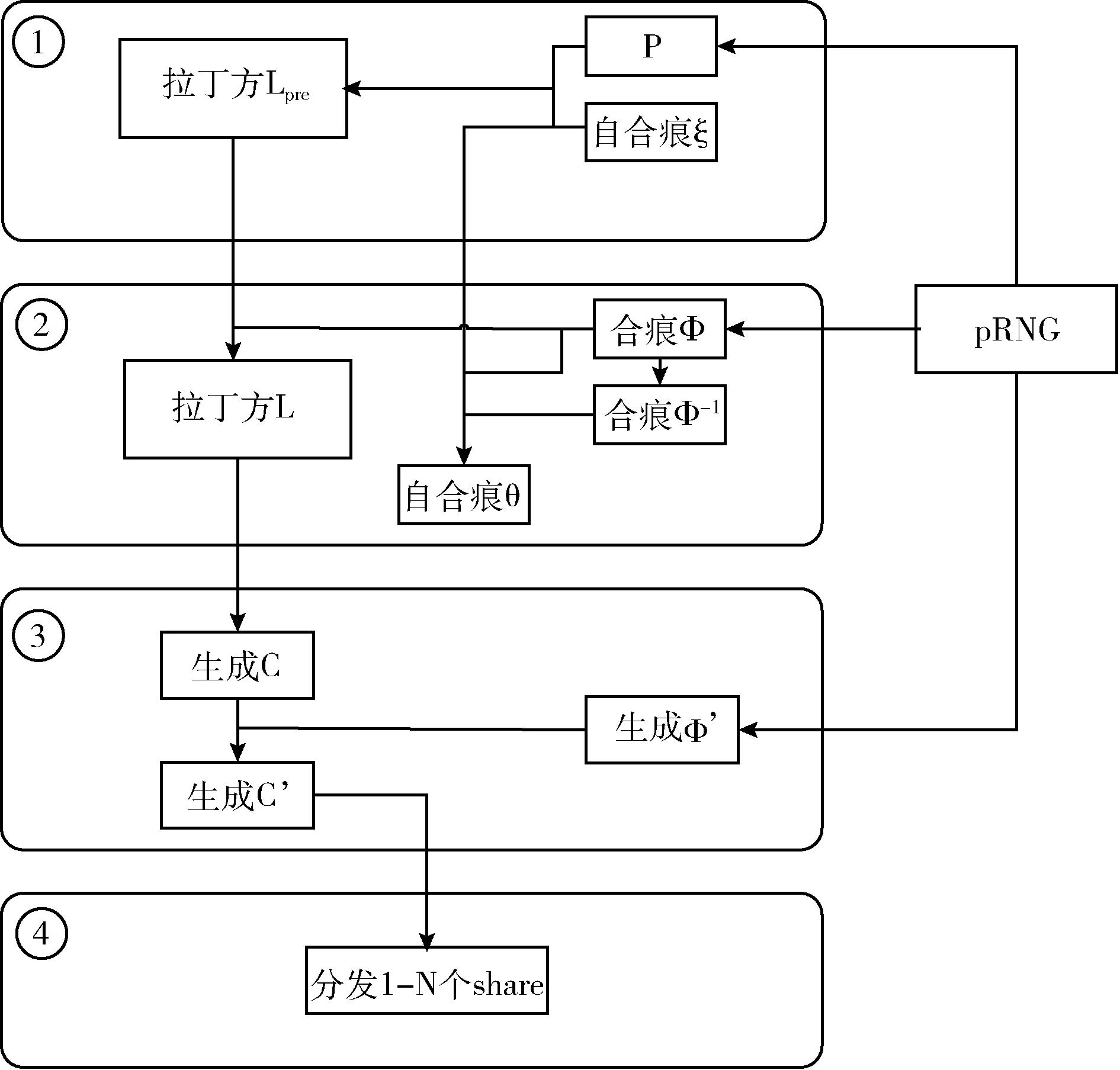
图4 方案初始化流程

2.2 秘密拉丁方L的重构

秘密拉丁方L的重构是初始化的逆过程，首先收集部分参与者持有的“share”分片结合组成C’，由随机合痕Φ’经过运算得到Φ’-1。C’与Φ’-1经过循环置换的逆过程得到轮廓C，C与自合痕θ利用算法1恢复秘密拉丁方L，进而得到秘密S。方案的主要过程有以下两步：

步骤1 根据(K,N)门限秘密共享方案的要求，任意收集K到N个参与者持有的share分片组合起来得到C’，同时得到自合痕θ与合痕Φ’，将合痕Φ’求逆得到Φ’-1

θ=((053)(124),(032)(154),(024)(135))， Φ’-1=((541),(25341),(3241))；

C’与Φ’-1经过循环置换的逆过程得到轮廓C

步骤2 将轮廓C中的元素使用三元组表示，与自合痕θ结合，使用算法1根据拉丁方的定义经过循环置换后就能够重构秘密拉丁方L，得到秘密S。以下是轮廓C中的三元组集合通过自合痕θ进行循环置换的详细步骤

通过上述的运算可以得到秘密拉丁方L各个位置元素的三元组集合，因此就能重构秘密拉丁方L，得到秘密S

在之前的秘密共享方案中，一个很重要的问题就是无法保证收集share分片的正确性，由此恢复的秘密正确性受到质疑。在本文秘密拉丁方的重构过程中，如果得到的轮廓C与自合痕θ不能重构拉丁方L，证明收集的share分片出现了错误，需要重新收集正确的share分片。换句话说，拉丁方L具有“自检测性”。这个特性避免了使用错误的share分片去重构拉丁方L，并且对于恢复秘密的正确性也有足够的保证。图5描述了秘密拉丁方L重构S的流程。

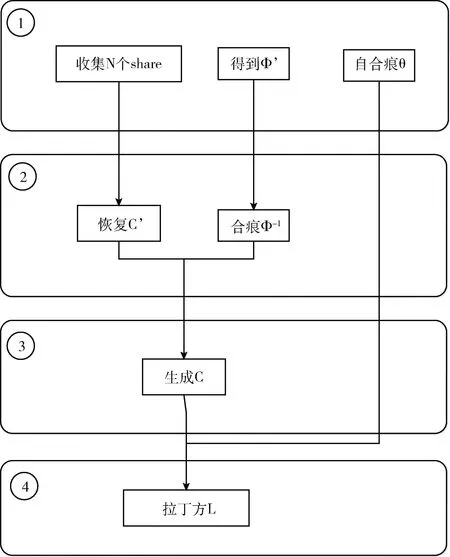
图5 方案重构流程

2.3 分片泄露后的秘密保护措施

以往的拉丁方秘密共享方案中没有考虑秘密分片泄露后如何进行秘密的恢复保护。例如一个参与者不小心把自己持有的share分片泄露出去，某些不怀好意的攻击者极有可能利用这些泄露的share分片进行攻击从而得到需要保护的秘密。为了秘密的安全，需要将这些有可能泄露的秘密进行替代或者使用新的方法再次进行加密，这个过程是非常耗费时间以及其它资源的。能否在share分片泄露后丢弃这些具有潜在泄密风险的share分片，同时进行share分片的更新，使用新的share分片来进行秘密共享，在不更换秘密的情况下尽最大可能进行秘密的保护是值得考虑的。

本文的拉丁方秘密共享方案可以有效解决这一问题，假如部分share分片由于某些未知原因丢失或者泄露，为了保护秘密的安全，可以实行以下“分片泄露后的秘密保护措施”，对本方案进行如下的改进：

(1)即对于泄露的分片，同样将它们收集起来，运行秘密拉丁方L重构过程的第一步：利用门限秘密共享方案将δ1-δN收集起来组成C’，运行恢复过程C=Φ’-1(C’)得到轮廓C，将失去作用的C’和Φ’丢弃。

(2)重新生成一个随机合痕Φ’，重复初始化过程的第3、4步，再将轮廓C使用Φ’进行合痕转换生成新的C’，对C’构造门限秘密共享方案进行重新分发。

例如：假若由于某些原因载有秘密信息的share分片泄露，先采取措施(1)，通过拉丁方重构过程中的第一步得到轮廓C

再采取措施(2)，重新生成一个新的合痕Φ’=((2543),(13245),(254)，得到新的C’

得到C’后通过初始化阶段的步骤4进行秘密分片的重新分发。对于秘密拉丁方L的恢复则通过拉丁方的重构过程。使用分片泄露后的秘密保护措施，无需修改轮廓C，也不用更新秘密拉丁方L就能得到新的share分片，避免了秘密分片泄露带来的安全隐患。如果分片没有泄露，也可以进行分片的定期更新，处于动态变化中的share分片有力提高了秘密共享方案的安全性。

本文中拉丁方秘密共享方案的一个潜在的重要应用是将秘密拉丁方L作为加密密钥，share分片的更新措施可以用于加密密钥的保护。通过该拉丁方秘密共享方案将密钥分片进行分发，若部分密钥分片泄露或者丢失，可以将泄露的密钥分片进行丢弃、更新操作。通过该方案，可以在不改变加密密钥的情况下进行密钥分片的更新，避免了密钥更新带来的重新解码加密数据、生成新的加密密钥、再进行重新加密的巨大工作量，有力保护了密钥与加密数据的安全，节约了大量的时间资源。

3 方案分析

3.1 安全性分析

(1)暴力攻击

攻击者可能会使用大量的计算资源通过系统的组合秘密的所有可能性，直到得到秘密。对于拉丁方秘密共享方案来说，为得到秘密拉丁方L，攻击者会使用暴力攻击手段对一个n阶拉丁方的所有可能排列进行一一遍历，直到得到所需要的秘密拉丁方L。尽管在理论上存在这种可能性，但是在实际情况下一个n阶拉丁方的合痕类数量是非常巨大的。例如一个n阶拉丁方阵，第1行有n!种填充方式，对于第2行第1列，有n-1个数字可以填充，第2行第2个数字有n-2种填充方式，以此类推：拉丁阵第2行一共有(n-1)!种填充方式。第3行有(n-2)!种,…,第n行有2!种。因此对于一个n阶拉丁方阵，符合要求的拉丁方阵数量是：n!(n-1)!(n-2)!…2!。以下是阶数n在8到12的拉丁方及其合痕类的数量

n=8:数量：108,776,032,459,082,956,800； n=9:数量：9!×8!×7!×6!×5!×4!×3!×2!； n=10:数量：10!×9!×8!×7!×6!×5!×…×2!；

n=11:数量：11!×10!×9!×8!×7!×6!×5!×…×2!；

n=12:数量：12!×11!×10!×9!×8!× 7!×6!×5!×…×2!；

根据现有的知识，得到阶数n较大的拉丁方的全部可能排列是非常困难的，因此在数量如此巨大的拉丁方中通过使用暴力攻击的方式对n阶拉丁方的全部可能排列进行一一遍历，进而来找到秘密拉丁方是几乎“不可能”的。因此可以认为该拉丁方秘密共享方案是足够安全的，可以有效抵御攻击者的暴力破解攻击。

(2)部分参与者的背叛

对于(K,N)门限秘密共享方案来说由K个或多于K个参与者所持有的share分片上的信息可以重构秘密S，而少于K个参与者持有的share分片就无法得到秘密S。

本文中的拉丁方秘密共享方案中使用了门限秘密共享方案进行share分片的分发，因此如果其中一部分参与者共同发生背叛行为，将自身持有的share分片结合起来，对秘密拉丁方L进行恢复，这在理论上是可行的，但必须要求有K个或者K个以上的参与者共同背叛才能达到这种效果，少于K个参与者持有的share分片上的信息无法进行秘密拉丁方L的重构，即不可能得到秘密拉丁方L。例如拉丁方秘密共享方案中在share分片分发阶段构造的(4,5)门限方案中，只有4个及4个以上的参与者共同背叛，它们持有的share集合所包含的信息才能够得到轮廓C，而少于4个的share组合并不能得到秘密拉丁方L。因此在拉丁方秘密共享方案中部分share分片信息的泄露不会影响秘密拉丁方L的安全，但为了避免这种潜在的风险，要求在选择参与者的时候应尽量避免这种大规模参与者背叛情况的发生，从而保证秘密的绝对安全。

(3)C’丢失

在循环结构(n/2)(n/2)下，n次对成群Sn中的可能的置换数量是“n!(2!(n/2)2)=2(n-1)!/n”。因此，n阶拉丁方L的合痕类数量可以表示为“(2(n-1)!/n)3”。n阶拉丁方L的自合痕θ的集合用“Atp(L)”表示，通过“轨道-稳定集”定理，n阶拉丁方L的合痕类数量也可以表示为“is(L)=n!3/Atp(L)”[16]。

在已知n的情况下，表1给出了n阶拉丁方中合适的合痕、自合痕等数据。

表1 n阶拉丁方合痕、自合痕的数量

假设在某种情况下，共享的share全部丢失，被不法的攻击者获得，攻击者利用这些share分片得到了C’。为获得秘密拉丁方L，攻击者必须还要得到合痕Φ’与自合痕θ，从合痕类中猜测Φ’的正确则的概率是1/is(L)，由表1可知：即使是在n=10的情况下这种可能性也是非常小的。这样就很难从C’中得到正确的轮廓C，因此通过暴力攻击手段得到轮廓C是不可能的。即使在某种可能性很小的情况下攻击者得到了Φ’，进而得到了轮廓C，但是没有自合痕θ的参与恢复拉丁方L同样是不可能的，这样的秘密保护机制被称为“双重防护”。此外，还可以对自合痕θ和合痕Φ’进行切割后随机的分发给参与者，没有二者的参与同样不能恢复秘密，进一步提升安全性。

3.2 秘密共享方案的多级方案

在信息系统中很多有重要价值的信息往往需要进行加密来保护信息的安全，信息的使用者需要在密钥的配合下对密文进行解密操作才能获得想要的信息。对于加密后的重要数据，不怀好意的攻击者需要使用一切手段获得加密密钥，一旦密钥丢失，密文就会有极大的概率丢失，因此对于加密密钥的保护是信息系统的重中之重。为了保证密钥的绝对安全，需要将密钥分发给具有不同权限级别的参与者。只有不同权限级别的参与者共同分享自己持有的子密钥时才能得到原始密钥，换句话说，任何一个参与者仅仅通过自身持有的子密钥并不能得到唯一的密钥，因此秘密共享方案在密钥保护方面也有潜在的应用。

使用本文中的拉丁方秘密共享方案，可以构造安全性更高的秘密保护的多级方案。如图6所示，秘密拉丁方L作为一个密钥K，恢复L需要3部分数据的协助，包括“C’，θ和Φ’”。拉丁方秘密共享方案将C’进行分发，对于θ，Φ’来说，是公开的(但这种公开是有条件的，仅仅向获得权限的参与者公开，无权限人员并不能得到该数据)。在秘密共享的多级方案中，放弃这种公开，并且规定了两种级别的权限：高级权限P1与普通权限P2。P1所持有的share分片重要性高于P2。随后将自合痕θ与Φ’分发给P1级的参与者，C’分发给P2级别的参与者。只有P2级的参与者结合生成的C’与P1级的参与者持有的自合痕θ与Φ’相结合，才能恢复秘密拉丁方L，进而得到密钥K。3个条件缺少其中的任何一个，均不能得到密钥K，这极大提高了密钥K的安全性，同时为拉丁方在秘密共享的多级方案应用提供了可能。

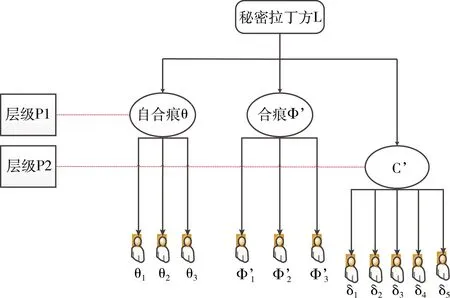
图6 秘密共享的多级方案

4 结束语

本文提出了一种拉丁方秘密共享方案，利用拉丁方的轮廓与合适自合痕可唯一恢复该拉丁方的特性，将具有自合痕转换性质的拉丁方作为“秘密”，将合痕转换后的轮廓进行秘密共享。本方案使得拉丁方秘密共享方案的初始化和秘密重构简单易行，同时减少了秘密共享过程中数据的规模，避免了秘密分片的直接暴露，增加了秘密的安全性。随机选择轮廓中三元组的数量构造(k,N)门限秘密共享方案，为秘密提供了足够的冗余来提高方案的容错性，解决了早前拉丁方秘密共享方案任何一个秘密分片丢失后秘密就会完全丢失的问题。同时该方案还在秘密共享的多级方案、秘密分片泄露保护等方面进行了推广。

本文的拉丁方秘密共享方案仅仅考虑了在n=2(mod 4)的情况下，未来的一个研究方向是将n进一步推广到任意的正整数值。另外秘密共享方案共同的不足在于返回过程中识别哪些share是不正确的，在该方案中，错误的share组成的轮廓在恢复阶段是不能得到唯一拉丁方的，但这个验证发生在了恢复的最后阶段，能否在share收集阶段验证其正确性也是值得思考的。