基于聚类的代理模型构建策略

陈 彧，杨媛媛

(武汉理工大学 理学院，湖北 武汉 430070)

0 引 言

代理模型辅助的进化算法(surrogate-assisted evolutionary algorithm，SAEA)在昂贵单目标和多目标优化问题中得到了广泛的应用[1,2]，代理模型的选择、构建和管理是SAEA的设计和应用中的关键技术问题[3]。为克服单一代理模型的缺陷和不足，Sun等[4]采用多代理模型提高代理模型的评价精度。为减少多代理模型导致的计算量的增加，Shu等[5]采用多精度模型来实现迭代过程的探索和开发需求，Yu等[6]则通过动态模型选择策略构建低复杂度的面向搜索需求的代理模型。在训练数据集的扩展方法方面，Tian等[7]采用多目标加点准则进行训练数据选择，可以在互相矛盾的需求中取得较好的折衷。Wang等[8]根据进化算法的全局探索和局部开发需求分别构建代理模型，但未对训练数据进行筛选，从而导致了模型训练过程时间复杂度的无限增长。

针对SAEA研究中的技术难题，本文提出了一种基于聚类的代理模型构建策略(clustering-based construction strategy of surrogate models，CCS-SM)。该策略采用了多代理集成模型的动态选择技术，利用聚类方法选择多精度模型的训练数据，并设计了面向搜索需求的加点准则。数值实验结果表明，基于CCS-SM策略的代理模型辅助粒子群优化算法(particle swarm optimization assisted by surrogates based on clustering，PSO-ASC)时间复杂度低，收敛速度快；另外，以基于CCS-SM的粒子群优化(particle swarm optimization，PSO)搜索作为一种加速策略，可以大大提高混合变量多目标进化算法(mixed-variable multiobjective evolutionary algorithm，MV-MOEA)的收敛性能。

1 基于聚类的代理模型构建策略(CCS-SM)

为实现基于代理模型的全局搜索和局部开发，需要构建全局代理模型和局部代理模型。本文提出了一种基于聚类的代理模型构建策略(CCS-SM)。

首先，通过聚类算法实现对搜索空间的自适应划分。本文采用K-means聚类算法来将已经得到的所有数据点分为N个数据类C1,C2,…,CN。

其次，基于聚类结果来构建全局代理模型。考虑到数据集中数据点的分布存在不确定性且代理模型本身存在近似误差，为得到能够刻画优化问题全局走势的全局代理模型，分别从C1,C2,…,CN中随机选择一个数据点来构成训练全局模型的训练数据集，试图通过数据点位置的随机性来削弱代理模型近似误差对全局搜索的不利影响。

同时，基于聚类结果构建局部代理模型。考虑到全局最优解以较大的概率存在于当前所搜索到的数据点中适应值较好的数据类附近，以Ci(i=1,…,N)中各数据点的最佳适应值作为类Ci的适应值，通过轮盘赌方式选择Ci0类数据所在的区域作为局部搜索区域。若Ci0类中的数据点个数M大于等于N，则选择适应值最好的N个数据点训练代理模型；否则，再从其它N-1个类中选择适应值最好的N-M个点，并在此基础上构建局部代理模型。

CCS-SM策略基于已有数据的聚类结果来构建全局和局部代理模型，对构建模型的数据集合规模进行了控制，降低了代理模型的训练和评价过程的时间复杂度；通过采样不同类的数据来构建的全局模型可以较好刻画待优化问题的全局适应值地形，而基于同一类的数据来构建的局部代理模型则具有较好的局部近似精度，能够实现低复杂度的高精度局部开发。因此，CCS-SM在对时间复杂度进行精确控制的前提下提高了全局代理模型和局部代理模型的构建效率，有望大大提高SAEA的收敛效率。

2 基于聚类的代理模型辅助粒子群优化算法(PSO-ASC)

基于CCS-SM策略的代理模型构建和管理模式，本文提出了一种基于聚类的代理模型辅助粒子群优化算法(PSO-ASC)。

2.1 PSO-ASC的集成代理模型

由于每一种代理模型具有各自的优缺点，PSO-ASC中采用3个典型的异构模型进行集成[8]：

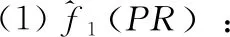
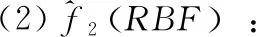
2.2 PSO-ASC的搜索策略

对于最小化问题minf(x)，PSO-ASC通过在3种不同的搜索模式之间进行切换来实现基于代理模型的启发式搜索。

2.2.1 搜索模式一

(1)

作为最大化的目标函数，利用PSO寻找集成代理模型评价的不确定性较大的点。对PSO搜索得到的最优结果进行精确评价，并将其加入数据集中。

2.2.2 搜索模式二

利用代理模型加速收敛，构建能够较好刻画优化函数的全局适应值地形的全局代理模型。通过CCS-SM的全局策略选择构建全局代理模型的N个数据点，并从3个代理模型中随机选择一种作为全局代理模型

(2)

式中：j为1-3的随机整数。基于所建立的全局代理模型(2)，利用PSO寻找全局代理模型评价目标函数值较小的点。对PSO算法得到的结果进行精确评价，将其加入数据集中。

2.2.3 搜索模式三

利用局部代理模型进行局部开发，建立尽可能精确的局部代理模型。通过CCS-SM策略的局部策略选择构建局部代理模型的N个数据点，以模型(2)作为最小化的目标函数，利用PSO进行基于代理模型的局部搜索。对PSO搜索到的最终结果进行精确评价，并将其加入数据集中。

2.3 PSO-ASC算法的迭代过程

基于上述3种搜索模式，本文提出了一种基于聚类的代理模型辅助粒子群优化算法(PSO-ASC)。基于图1所示的算法框架，PSO-ASC的具体迭代过程如下：

图1 PSO-ASC算法框架

(1)采用拉丁超立方抽样(Latin hypercube sampling，LHS)生成种群规模P=P0的初始种群，并对其进行精确评价；将其加入档案数据集Dt，其中P表示数据集的规模。

(2)根据模式一从Dt中选择N个数据点训练全局代理模型；采用LHS重新产生N个数据点生成初始种群，以式(1)的函数最大化作为优化目标，采用PSO算法进行迭代优化；对PSO优化的结果进行精确的个体评价，并将其加入Dt中，得到新的数据集Dt+1；

(3)根据模式二的策略从Dt+1中选择N个数据点训练全局代理模型；采用LHS重新产生N个数据点生成初始种群，以式(2)中的函数最小化作为优化目标，采用PSO算法进行迭代优化；对PSO搜索得到的结果进行精确的个体评价，并将其加入Dt+1，得到新的数据集Dt+2；

(4)令t=t+2；如果t≥tmax，算法结束；否则，如果Dt中的最佳适应值得到改进，则转到(2)；如果Dt中的最佳适应值未得到改进，则转到(5)；

(5)根据模式三的策略从Dt中选择N个数据点训练全局代理模型。采用LHS重新产生N个数据点作为初始种群，以式(2)中的函数最小化作为优化目标，采用PSO算法进行迭代优化；对PSO搜索得到的结果进行精确的个体评价，并将其加入Dt中得到新的数据集Dt+1；

(6)令t=t+1；如果t≥tmax，算法结束；如果Dt的种群适应值得到改进，则转到(5)，否则转到(2)。

2.4 数值实验

2.4.1 参数设置

为验证本文所提出的PSO-ASC算法的有效性，我们通过表1所示的5个标准测试函数将其与CAL-SAPSO的实验结果进行了比较。两个算法都采用了同样的参数设置：对于问题规模为d的测试问题，初始数据集规模设为N=5d，个体精确评价次数上限为11d；在基于代理模型的PSO搜索中，种群规模为50，迭代次数为100。为了对比两个算法在不同规模的测试问题的求解效率，对于每个测试问题都对比了d=10，20，30这3种情况。

表1 测试问题

2.4.2 结果分析

为验证算法PSO-ASC的有效性，本文通过数值实验将其与4种有代表性的经典SAEAs进行了比较。其中，GPEME[9]和MAES-ExI[10]均以Kriging模型作为代理模型，分别采用置信下界(lower confidence bound，LCB)和期望改进量(expected improvement，ExI)作为精确评价及加点准则；WTA1[11]和GS-SOMA[12]均采用了多项式回归(polynomial regression，PR)、径向基函数(radial basis function，RBF)网络和Kriging模型构成的集成模型，而GS-SOMA还额外采用了一个PR模型来对数据进行光滑处理。对每一个测试问题独立运行PSO-ASC 20次，5种算法所得到的目标函数平均值与标准差见表2，其中黑体表示所有算法比较的最佳结果。除了Rosenbrock函数外，PSO-ASC的平均结果大多优于其它算法，但运行结果的标准差却往往略差，特别是对于Rosenbrock函数的优化结果平均值与标准差均高于GS-SOMA。考虑到Rosenbrock函数的适应值地形具有狭长的平缓波谷，对优化算法的种群多样性的要求更高，而GS-SOMA能够更好的在收敛过程中保持种群多样性，故在Rosenbrock函数的优化问题上表现更好。

表2 PSO-ASC与GPEME、MAES-ExI、WTA1和GS-SOMA的运行结果(平均值±标准差)比较

需要注意的是，由于PSO-ASC的设计初衷是对精确评价尤其困难的数据驱动优化问题进行高效优化，故采用了与以上算法不同的基于代理模型评价结果的连续多次迭代模式。为了更进一步发掘PSO-ASC中的CCS-SM策略的优势和不足，我们将其与CAL-SAPSO算法[8]进行了比较。CAL-SAPSO采用了与PSO-ASC类似的迭代模式，但其采用集成模型对个体进行近似评价，且将所有已有的数据点作为训练数据来构建代理模型。

对每个测试问题独立运行20次，分别计算20次迭代过程中每一代的目标函数平均值，可以得到算法的收敛曲线。将PSO-ASC和CALS-SAPSO分别求解d=10，20，30的5种测试问题，可以得到图2所示的Ackley函数的收敛曲线、图3所示的Ellipsoid函数收敛曲线、图4所示的Griewank函数收敛曲线、图5所示的Rastrigin函数收敛曲线及图6所示的Rosenbrock函数收敛曲线。由于两种算法采用了相同的初始化模式，在1～5d次个体评价的收敛曲线大致相同。从第5d+1次精确评价开始，CAL-SAPSO算法的收敛曲线瞬间发生了大幅下降，在迭代中期的快速收敛以后，迭代后期迭代曲线趋于平稳，收敛过程出现停滞；相对而言，PSO-ASC算法的下降过程则是连续的，在迭代中期下降速度比CAL-SAPSO算法慢，但却能够在迭代后期保持适应值的持续下降，最终得到比CAL-SAPSO算法更好的收敛结果。由于CAL-SAPSO算法采用所有的数据点来构建代理模型，可以在迭代中期引导算法的快速收敛；然而，倘若迭代前期所得到的数据点的分布具有局限性，则可能导致CAL-SAPSO在中期所得到的数据点大多集中于某个区域附近。到了迭代后期，处于这个区域的数据点规模较大时，在代理模型的构建过程中就会处于主导地位，导致迭代后期算法一直在这一区域进行搜索。倘若这一区域是局部最优解的吸引区域，则会出现图3和图4中所示的停滞现象。而PSO-ASC算法在迭代搜索过程中总是根据聚类结果来选择数据构建代理模型，在迭代中期聚类结果随着迭代过程的推进变化较大，因此基于代理模型的搜索过程主要关注于全局探索，最佳适应值的变化速度较慢；因此，PSO-ASC算法得到的数据集具有更好的多样性，在迭代后期则能更好的克服局部最优解的吸引，最终得到更加精确的近似最优解。

图2 CAL-SAPSO、PSO-ASC优化d=10,20,30的Ackley函数的收敛曲线

图3 CAL-SAPSO、PSO-ASC优化d=10,20,30的Ellipsoid函数的收敛曲线

图4 CAL-SAPSO、PSO-ASC优化d=10,20,30的Griewank函数的收敛曲线

图5 CAL-SAPSO、PSO-ASC优化d=10,20,30的Rastrigin函数的收敛曲线

图6 CAL-SAPSO、PSO-ASC优化d=10,20,30的Rosenbrock函数的收敛曲线

考虑两种算法独立运行20次所得到的最终状态，其运行结果平均值、中位数、标准差，以及两种算法的平均运行时间见表3。表3中的对比结果表明，PSO-ASC算法求解测试问题的最终结果的平均值和中位数均优于CAL-SAPSO算法。由于PSO-ASC在迭代中期的全局搜索过程得到了分布更好的数据点集，算法能更好地克服全局最优解的吸引，从而可以得到更精确的全局最优解。因此，PSO-ASC算法需要更多的迭代预算来实现种群的收敛，在迭代次数还不能达到其种群收敛要求的情况下，PSO-ASC算法求解结果的标准差会略高于CAL-SAPSO。然而PSO-ASC算法对代理模型的构建数据集规模进行了控制，在搜索模式二和模式三中均随机采用集成模型中的一种模型进行评价，与CAL-SAPSO算法相比虽然所构建的代理模型精度略微下降，但基于代理模型的搜索过程的时间复杂度却大大降低。因此，PSO-ASC最终结果以标准差略大的代价，获得了更低的时间复杂度，其整体性能优于CAL-SAPSO。

表3 PSO-ASC与CAL-SAPSO对测试问题的运行结果比较

3 代理模型辅助的混合变量进化算法(SaMV-MOEA)及其在S-系统推断中的应用

3.1 非线性S-系统及其双目标优化模型

非线性S-系统是一种能够较好地刻画生化反应的非线性动力学性质的微分方程模型。有N种物质参与反应的生化网络S-系统如下

式中：Xi为第i中反应物的浓度，αi,βi,gij,hij为模型参数。然而，S-系统中的模型参数较多，变量Xi对模型参数的适应度地形非常复杂，而在最优参数值附近反应物Xi的浓度对参数又极不敏感，因此对稀疏S-系统的推断非常困难。文献[13]采用二进制变量刻画生化网络的网络连接关系，构建了推断S-系统的N个方程进行逐个推断的双目标优化模型

minF(θi)=(err(θi),L0(θi))

(3)

式中：θi=(αi,βi,gi1,…,giN,hi1,…,hiN)为第i个方程的参数向量，err(θi)为根据参数向量θi所计算出的数据拟合误差，L0(θi)为参数向量θi的L0范数。为了更加容易得到稀疏的网络连接，采用二进制向量表示网络连接，实数变量表示具体的参数值，并设计了混合变量的多目标进化算法(mixed-variable multiobjective evolutionary algorithm，MV-MOEA)对S-系统来进行求解。在对表4中的S-系统的每个微分方程进行逐个推断的数值实验中，MV-MOEA在2000次个体评价以后得到了更精确的推断结果[13]。

表4 5维S-系统的模型参数

3.2 代理模型辅助的混合变量进化算法(SaMV-MOEA)

由于MV-MOEA在迭代过程中生成了大量的候选解并对其进行了精确评价，充分利用已搜索到的历史结果来构建代理模型，可以提高MV-MOEA的全局收敛速度和局部开发能力。为此，本文将CCS-SM策略引入MV-MOEA，得到一种代理模型辅助的混合变量多目标进化算法(SaMV-MOEA)。

由于MV-MOEA采用了不同的方式来生成候选解中的二进制串和实数向量，在通过变异生成二进制串以后，可以采用代理模型来提高实数向量的生成效率。首先，在MV-MOEA中增加档案集A，保存所搜索到的所有候选解。对于档案集A中的任意一个解x=(bx,rx)，bx为N维二进制串，rx为N+2维实数向量。令

θ=(rx(1∶2),bx),bx⊗rx(3∶N+2)

(4)

式中：bx⊗rx(3∶N+2)表示bx与rx(3∶N+2)逐个分量相乘。于是可以得到由参数向量θ构成的代理模型训练数据集Dt。

在SaMV-MOEA的新个体生成策略中，根据CCS-SM策略构建全局或局部代理模型，并基于此代理模型进行小种群规模，低迭代次数的PSO搜索。最后，将PSO得到的实数解向量与MV-MOEA中的变异策略生成的实数解向量分别通过式(4)和MV-MOEA的二进制变量生成策略得到的二进制串进行结合，从而得到优化模型(3)中的参数向量θ。通过err(θi)对两个实数向量串进行比较，将对应的适应值较好的实数向量作为新个体的实数向量，从而提高实数解向量的生成效率。

考虑到基于代理模型的迭代搜索过程也具有一定的时间复杂度，我们将代理模型辅助的迭代搜索的种群规模设为20，迭代次数设为50。另外，为进行公平的比较，SaMV-MOEA和MV-MOEA的种群均设为100。对于表4中S-系统进行数值实验，SaMV-MOEA经过1000次迭代和MV-MOEA经过2000次迭代的数值结果见表5。

表5 SaMV-MOEA与MV-MOEA对S-系统的推断结果比较

数值实验结果表明，通过引入代理模型能够提高实数向量的生成效率，虽然SaMV-MOEA的迭代次数只有MV-MOEA的一半，但却得到了与其相似的推断结果。需要特别说明的是，对于第3个方程，SaMV-MOEA得到了比MV-MOEA更接近真实模型参数的推断结果。这说明在代理模型的辅助下，SaMV-MOEA对于具有平坦的适应值地形的优化模型具有更强的全局搜索能力，能够更快地收敛到全局最优解附近。

4 结束语

目前，对SAEA的研究工作主要集中于如何降低昂贵优化问题的精确评价次数，却较少关注如何利用低复杂度的代理模型来提高进化算法的收敛效率。本文提出了一种基于聚类的代理模型构建策略CCS-SM，并由此提出了CCS-SM策略的PSO-ASC和通过CCS-SM策略来加速收敛的SaMV-MOEA。数值实验结果表明，基于CCS-SM策略进行迭代搜索的PSO-ASC和将其作为加速策略的SaMV-MOEA的优化性能均优于已有的算法，表明该策略是一种高效的代理模型构建和管理策略，可以在各类代理模型辅助的进化算法中进行推广应用。