《算术之钥》与中算若干问题的比较研究

郭园园

(上海交通大学人文学院科学史与科学哲学系，上海 200240)

从花拉子米(al-Khwārizmi，约780 ～ 约 850)到阿尔·卡西(al-Kāshi，约 1380 ～1429)600余年的时间里，中世纪的阿拉伯数学家们取得了辉煌的成果。阿尔·卡西是阿拉伯数学史晚期最著名的数学家之一，《算术之钥》为其代表作，其内容包括算术、代数和几何，几乎涵盖了当时所有的数学分支，堪称一本初等数学大全，除了满足一般学生的需求外，对于从事实际工作的读者，如天文学家、测量员、建筑师、商人等也有帮助。该书分5卷，分别为:第1卷、整数的算术;第2卷、分数的算术;第3卷、天文学家的计算法(六十进制数码的算术);第4卷、图形的度量;第5卷、用还原与对消及双假设法等方法求解未知数。一方面由于阿拉伯世界地处中西交汇之处，包括《算术之钥》在内的众多阿拉伯数学经典中都包含了明显的东西方古老文明的痕迹;另一方面由于在中世纪阿拉伯帝国晚期，蒙古帝国的迅速崛起客观上提供了中国与阿拉伯地区间进一步交流的可能性，这些都有可能带来中阿数学知识的交流与传播，所以《算术之钥》与中算相似问题的比较研究一直是研究的热点问题。但是由于语言和史料的原因，国内学者长期依赖于国外二手文献;而国外的阿拉伯数学史工作者又缺乏对中算相对全面系统的了解，因此以往就此问题的研究往往只是就几个“散点”进行分析，还有很大的研究空间。本文作者从解读《算术之钥》的阿拉伯文本献入手，在前人的研究基础上对其与中算相似的高次开方等问题进行了进一步的探讨。

1 阿尔·卡西生平及《算术之钥》概况

阿尔·卡西(全名 Ghiyāth al-Dīn Jamshīd Mas'ūd al-Kāshī，或 al-Kāshānī)，生于卡尚(Kāshān，位于今伊朗)，1429年6月22日卒于撒马尔罕(Samarkand，位于今乌兹别克斯坦)，天文学家、数学家。卡西出生时正逢帖木儿(Timur，1336～1405)帝国迅速崛起阶段，由于连年的征战和帖木儿生前所推行铁血的军事政策导致帝国内的经济严重衰退，因此卡西从小便生活于贫困之中。与其他的中世纪科学家类似，卡西也是将其科学著作献给君主或权贵以获得经济上的资助。尽管卡西另有一份医生的职业，但是他仍将大部分的时间和精力用于数学与天文学的研究上。

撒马尔罕是中亚的一座古城，它后来成为帖木儿帝国的首都，沙鲁克(Shāh Rukh，帖木儿之子)及其子乌鲁伯格(Ulugh Beg，1394～1449)成为该城的统治者。乌鲁伯格本身就是一位伟大的科学家，精通天文，而且是科学、艺术的倡导者与保护人，并且试图将撒马尔罕建设成为一个巨大的文化中心。事实上，直至1449年乌鲁伯格被暗杀，在四分之一个世纪的时间里它成为东方最重要的科学中心。经过一段时间徘徊之后，卡西最终在撒马尔罕找到了自己的归宿，并成为乌鲁伯格最亲密的合作伙伴和顾问。尽管卡西在来到撒马尔罕之前就已经完成了一些较好的著作，但是他最优秀的作品还是在撒马尔罕完成的。1424年7月，他完成了《论圆周》(Risāla al-mu.hit.iyya，“The Treatise on the Circumference”)，书中体现了卡西非凡的运算能力，他将2π的值精确地推算到小数点后十六位;1427 年3 月2 日，他完成了《算术之钥》(Miftāh al-hisāb，“The key of Arithmetic”);他的第三本著作《论弦与正弦》(Risāla al-water wa'l-jaib，“The Treatise on the Chord and Sine”)完成的确切时间未知，在此书中卡西将sin1°的值推算到与其计算π相同的精度。

由于《算术之钥》是中世纪晚期质量很高的一本数学著作，因此在数百年的时间里它被反复传抄。《算术之钥》的阿拉伯文手稿现分别保存于圣彼得堡、柏林、巴黎、莱顿、伦敦、伊斯坦布尔、德黑兰、麦什德(伊朗)、巴特那(印度)、兰布尔(印度)、白沙瓦(巴基斯坦)，其中最重要的手稿分别位于圣彼得堡(Publ.Bibl.131)、莱顿(Univ.185)、柏林(Preuss.Bibl.5992 和 2992a，及 Inst.Gesch.Med.Natur.I.2)、巴黎 (BN.5020)、伦敦(BM.419)和印度(Office 756)［1］。

1888年，伊朗学者将卡西的著作搜集整理成书(Majmū)并于次年出版，其中包括《算术之钥》。据编辑者指出其使用了相关的五个手稿，但是主要依据莱顿手稿;1954年苏联学者将此版本译为俄文并出版①Al-Kashi，Mathematicheskie traktaty.B A Rosenfeld(trans).Rosenfeld and A PYouschkevitch(eds).Moscow∶Istorikomatematicheskie issledovaniya，Volumu VII，1954.其中《算术之钥》俄文译文位于13～326页.;1956年苏联学者又将其中的《算术之钥》及《论圆周》两本书编订成合集出版②Al-Kashi，Klyuch Arifemetiki;Traktat ob Okruzhnosti(The Key to Arithmetic;The Treatise on the Circumference).B A Rosenfeld(trans).Rosenfeldand.A P Youschkevitch(eds).Moscow∶Gosudarstvennoe Izdatel'stvo Tekhniko-teoreticheskoi Literatury，1956.其中《算术之钥》俄文译文位于7～262页，《论圆周》的俄文译文位于263～319页，随后是评注，最后位于428-568页附有《算术之钥》莱顿手稿的照片。拉希德认为这不是一个权威版本(［3］，201页)。;1968年，埃及学者以莱顿手稿为基础出版了一个阿拉伯文版本并附有阿文评注［2］，这也是本篇论文所使用的《算术之钥》研究底本;1977年叙利亚学者也出版了一个阿拉伯文版本①Jamshid al-Kashi，Miftah al-Hisab(Key to Arithmetic).al-Nabulsi(eds).Damascus:Ministry of High Education，1977.。

对于《算术之钥》的研究专著很少。德国数学史家勒基(P.Luckey，1884～1949)曾对其部分内容进行了翻译和研究，并留有一本德文专著②P.Luckey，Die Rechenkunst bei Gamsid b.Masud al-Kasi［M］.Wiesbaden:F.Steiner，1951.。法国数学史家拉希德(R.Rashed)结合七八十年代以来最新的阿拉伯数学史研究成果于1984年出版了一本法文版的关于阿拉伯算术和代数的专著③R.Rashed，Entre arithmetique atalgebra:recherchésur I'histoire desmathematiquesarabes.Paris:les Belles letters，1984.，其中对卡西的工作及其地位给出了新的评价，1994年此书被译为英文出版［3］。此外对于《算术之钥》的研究性论文也不多，下文在相关内容中会具体介绍。

2 高次开方题

高次开方问题在中算中起源于《九章算术·少广章》开方术，经后世中算家逐渐发展，到宋代贾宪时已经发展成一系列的成熟算法，这些内容主要包括:增乘开方法、立成释锁开方法、无理根的近似算法、“开方作法本源”图，以上内容在《算术之钥》中均有相似的内容。下面按照《算术之钥》中开方问题的行文顺序首先就增乘开方算法进行比较。

2.1 增乘开方法

据钱宝琮考证，中算增乘开方法最早见于宋代贾宪所著《黄帝九章算法细草》，并著文［4］就贾宪增乘开立方法进行详细分析，此处不再展开。1948年，勒基首次提出《算术之钥》中建立了开高次方的一般方法，与鲁菲尼-霍纳算法一致，由于卡西在书中并没有讲述此方法的来源，故认为他的思想可能源于中国宋代贾宪的增乘开方法［5］。勒基的观点曾长期占据主导地位，《算术之钥》1956年俄文译本的序言、1967年阿文版本的序言以及德克赫勒(A.K.Dakhel)的论文［6］中都重复了勒基的工作及结论(［3］，143页)。但是随着对12世纪阿拉伯数学家萨马瓦尔(al-Samaw'al，约1130～约1180)的研究④目前萨马瓦尔的主要相关著作有两本:一本是《代术珍宝》，1972年由S.Ahmd和R.Rashed共同校订出版，其为阿拉伯文版并附有法文简介，即参考文献［11］;另外一本是名为al-Qiwami fi al-Hisab al-Hindi(1172～1173)的有关印度算术的著作，此书全文已经遗失，但是其第3卷的手稿得以保存，见(［3］，143页)。，《算术之钥》中的高次开方、无理根的近似逼近以及算术三角形都可以在其中找到相同的内容，有些内容甚至可以直接追溯到10世纪阿拉伯数学家凯拉吉(al-Karaji，953～约1029)。

国内的研究，1966年，杜石然先生在俄文译本的基础上比较了两种算法，并指出:“……把阿尔·卡西的开方法与宋元时期的增乘开方法相比较，便可以很明显地看出期间的每一步骤完全相同……，我们认为，这种算法很可能是受到了中国宋元数学的直接影响”［7］。文中仅就《算术之钥》第1卷第5章中所载的开方法与宋元增乘开方法做了比较，但是译文不全，且在《算术之钥》第2卷、第3卷中对开方问题还有大量详细的术文，所以就此尚需进一步的研究。1984年，杜石然先生在另一篇文章中简要重复了以往的观点，并没有给出新的论证:“对al-Kashi《算术之钥》的研究可以证实书中的算法与贾宪所用的增乘开方法几乎完全相同，……看来似乎可以肯定，在al-Kashi的著作中确实存在着中国数学的影响”［8］。

《算术之钥》中的开方问题位于第1卷第5章(整数的开方)、第2卷第10章(分数的开方)和第3卷第5章(六十进制数码的开方)，前三卷占到全书篇幅的三分之一，相当于基础的算术知识。可以看出开方运算在当时仅是作为数学基础知识，算不上是较难的内容。在第1卷第5章中，卡西先后给出了“乘方”与“方根”的定义、乘方的名称及乘方次数与名称之间的互化关系。这里需要注意一点，当时的阿拉伯数学家对于较高次幂的乘方名称是通过“平方”与“立方”的累加来实现的，例如:今天的“四次方”在当时记为“平方平方”、“五次方”记为“平方立方”、“六次方”记为“立方立方”等。随后卡西指出如果某乘方能够得出某开方幂指数下准确的方根，则此乘方为有理数;反之为无理数。接下来为了便于表述运算过程，文中给出了有理数位和无理数位的概念，例如现要求Z+)，则从a的个位起，其第(nk+1)(K∈N)数位称为其有理数位，剩余的数位全部为其无理数位。随后便是开平方与开高次方的具体方法并分别给出一道例题加以说明。与中算不同的是，卡西并没有将开立方单独列出，这主要是由于开平方与开高次方均是由增乘开方法统一起来，对此卡西在高次开方的一般方法后指出:

上面的方法(开高次方方法)同样适用于求平方根，但是在本章的前面将其单独列出有助于初学者理解。(［2］，67页)

下面是卡西对于开高次方一般方法的叙述:

开高次方的情况:

首先写出被开方的数字，同开平方方法一样画出表格。如前所述，从个位数字开始将被开方数分节，其中每一节数字的个数等于所要求开方次数。在每两节之间用双纵线分隔开。其中每一节的第一个数位为被开方数的有理数位，剩余的数位称为其无理数位。随后在竖直方向分层，其层数等于开方次数，在每两层之间作出水平分割线。每一层宽度应该由实际计算的需要决定。上面一行称为“数行”，最下面一行称之为“根行”，(根行)上方是“平方行”，再上方是“立方行”，这样继续下去一直到“数行”，“数行”之上也就是表格最上方是“结果行”。另外也可以将数行下面的一行称为“第二行”，同理下面称为“第三行”，这样直至“根行”。

首先从最后一节开始，试求出最大的个位数字，可将其减去此数的乘方，即此个位数字开方次数的乘方。我们已经将(九个)个位数字分别从其平方到平方平方立方立方(十次方)的一系列乘方列在了另一个表格中，这样便于求出上述数字。

如果找到了这个数，则将其写在结果行中最后一个有理数位上，另外还需写在根行与其对应的位置，随后用上面的数字乘以下面的数字，将结果即此数的平方写在平方行，其个位数字与根行中的个位数字对齐，(这几个数字的个位均)位于最后一个有理数位所在列上，如果(刚才的乘积)有十位，则写在(左侧)另外一列上。

随后用上面的数字乘以平方行中的数字，将所得的结果即(结果行中数字的)立方写在立方行中，剩余的过程如上，这样一直计算到第二数行，此时得到的各行中的结果实际上就是此数的一系列连续不同次数的乘方。

用上面的数字乘以第二数行中的数字，得到的结果是此数开方次数的乘方，随后用数行中对应的数字将其减去;接下来为了得到第二数行中的结果，用上面的数字再次加到根行中的数字上;随后用上面的数字乘以此时根行中的和，将结果加到上方的平方行中;随后同样用上方的数字乘以平方行中的和，将结果加到立方行①原阿拉伯语莱顿手稿中为平方行，应改为立方行，参考文献［2］已将其改正。，这样直至加到第二数行。此时为了得到第三数行中的结果，再次用上面的数加到根行中的数字上;随后用上面的数字乘以根行中的结果，将其加到上面一行，这样一直到第三数行结束。

为了得到第四数行中的结果，第三次用上面的数加到根行中的数上。重复这样的过程，直至进行到根行，即用上面的数字加上最后根行中的数字。随后将第二数行中的数字向右移动一位，将第三数行中的数字(向右)移动两位，下一行移动三位，依此下去直至根行结束，即根行在数行下几层，就应向右移动几位，最后根行中个位数字应与数行中最后一个有理数位前面一个有理数位的前面一位数字对齐(即第二节中的十位)。

这种方法就是将上面的数字分别乘以每一行中的数字，把结果加到上面一行，最后再用数行中的数将此结果减去。对于每一行的乘法运算与其中一个乘数是个位数字的乘法运算相同。随后将结果加到上一行中的数字上，使其个位与上面的乘数对齐，即位于上方此节的第一列中，在此之前要在二者之间作出分割线用以表示线下方的数字将被擦去;但是在数行中不是如此，在数行中将乘积写在(被开方)数之下，然后将它从其中减去，在下方写上二者的差，在此之前要在二者之间做一条分割线用以表示在线以上的部分将被擦去。

此时对于数行中分割线以下剩余数字的处理方式同前，在数行中的运算方向应该是由上至下，而剩余的行中的运算方向则是由下至上。随后由数字一开始再次寻找最大的个位数字(即次商)，将其写在结果行最后一个有理数位的前面一个有理数位上(即第二节的个位数字)，同时写在下面根行中分隔线上方已有数字的右边一位上。用它乘以根行中数字，将结果加到平方行中，随后用上面的数字同样乘以平方行中的和，将结果加到立方行中。

这样一直下去直至第二数行，接下来用上面的数字(即次商)乘以此行中的数字和，并按照前面所述的方法用数行中对应的数字将结果减去。减法运算之后，将上面的数字加到根行中分割线之上的数字，随后按照前面的方法逐行运算，并将各行中的数字进行移动。如果没有这样的数字(即次商)，则在表格上方前面提到的数位上写零，并将所有行中的数字再次进行移动。然后按照上面的方法继续运算，直至(计算到被开方数的)第一位。随后按照前面的方法将结果从数行中减去，如果在数行中分割线下方没有剩余数字，则此要求的(被开方)数为有理数，结果行中的数字即为其方根。(［2］，66～67页)

对此书中给出了一道求例题，即求44，240，899，506，197的平方立方根(即五次方根)，书中的演算过程如下②此数表见参考文献［2］，69页;笔者仅将其中的阿拉伯文及东阿拉伯数码进行翻译，表格的排列顺序未作修改。:

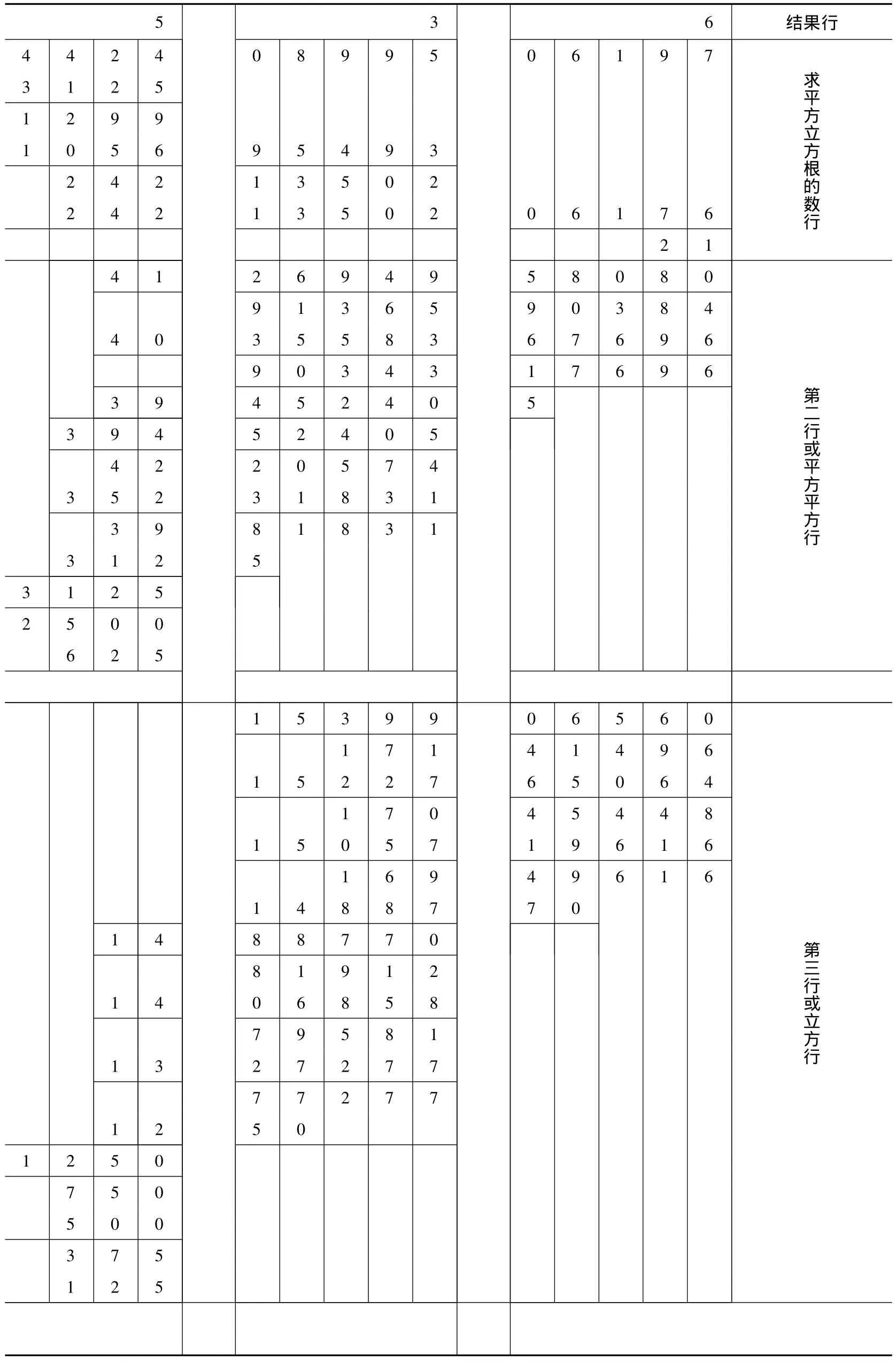
?536结果行442408995061973125求平1299方105695493立方24213502根的2421350206176数行214126949580809136590384403558367696903431769639452405第二39452405行4220574或平35231831方平3981831方行31253125250062515399065601714149615227650641704544815057196161694961614887701488770第81912三1406858行或79581立方1327277行7727712501250750500375125

续表

在《算术之钥》第3卷第5章中对于六十进制数码的开方问题给出了类似的详尽算法并附有一道开平方、一道开立方和一道开立方立方(即六次方)问题，下面以开立方问题为例进行说明，现要求:18，52;59，43，51，25①卡西在《算术之钥》中为了表述六十进制数码或是十进制小数，通常数字后加上一个单位名称用以表示最后一位数字的单位。例如此处卡西在数字25之后加上单位名称“，即表示25 的单位为“60－4”，其前面的数字单位依次类推。的立方根，演算数表如下②见参考文献［2］，119页.笔者仅对数表中的阿拉伯文进行翻译，并未改变数表的排列顺序。:

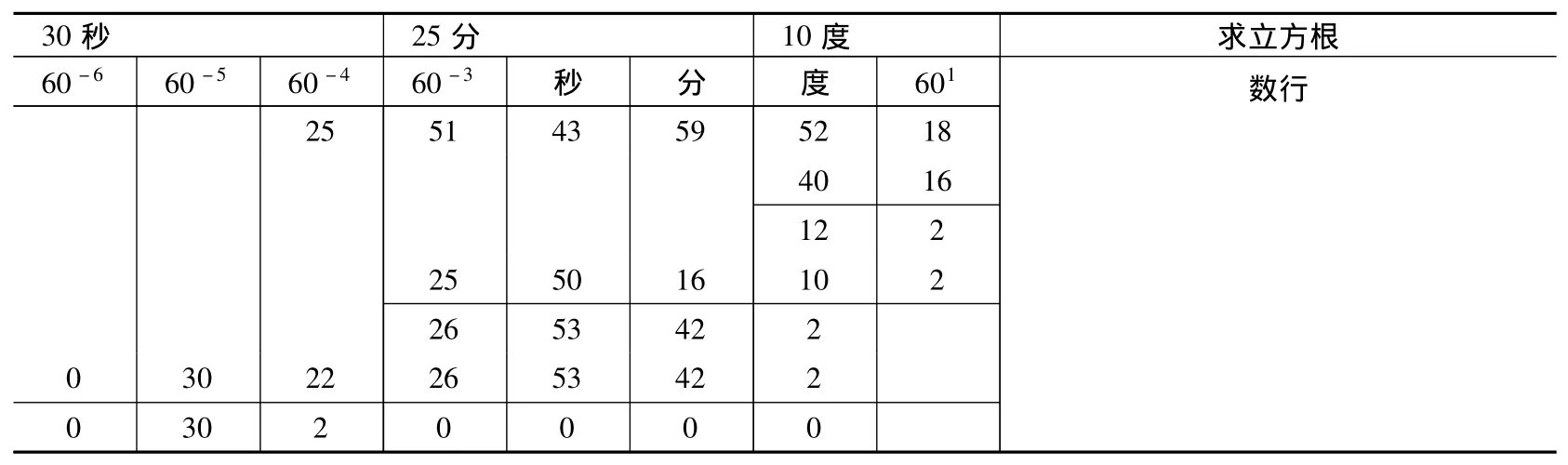
?30秒 25分 10度 求立方根60－6 60－5 60－4 60－3 秒 分 度 601数行2551435952184016122255016102265342203022265342203020000

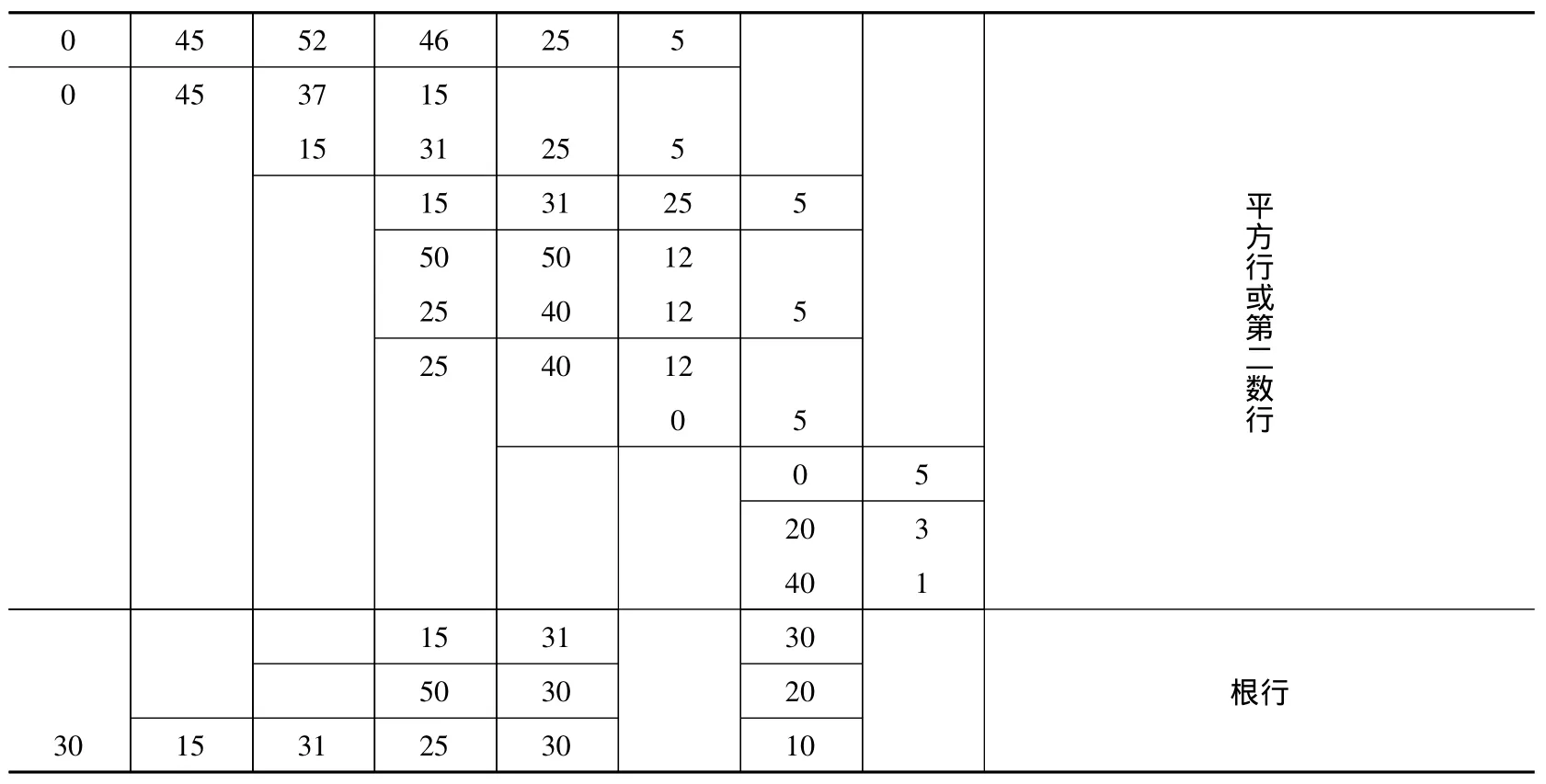
续表

通过观察不难发现对于第1卷整数中的开方问题和第3卷六十进制数码的开方问题在具体演算过程中有三点不同:

(1)对于整数的开方问题利用的是印度数码①卡西所使用的印度数码我们习惯上称之为东阿拉伯数码，其对应的1～9九个数字的书写分别为:，今天的东阿拉伯数码中的零用点来表示，卡西当时用空心小圆圈来表示数字零。东阿拉伯数码为当今阿拉伯世界的通用数码。进行书写，其书写顺序与今天国际通用的阿拉伯数码书写顺序相同，因此开方顺序也是从左至右进行;而六十进制数码则是利用按照闪语字母表顺序排列的阿拉伯语字母表示②闪语，是古代美索不达米亚语言的一个支系，当时，说这种语言的有好几个民族，阿拉伯人、以色列人和埃塞俄比亚人，现代阿拉伯语由闪语演化而来。1～9九个数码分别对应于字母;10～60整十的6个数码分别对应于字母，剩余的数码为这些字母的组合。，书写及运算方向与前者恰好相反;

(2)六十进制数码开方过程中的被开方数及结果行中方根的每一数位上的数码均需加上单位名称加以区分。卡西在算法术文中指出，方根中“度”数位必须与被开方数中“度”数位对齐，其余数位上的单位则要按照连续上升或者下降的单位名称进行书写。而对于十进制整数数码的开方过程则没有任何单位名称，由此可知一方面对于十进制数码开方运算过程中每一位上的单位很容易确定，故没有必要将其写出;另一方面被开方数中的个位数字必须与方根中的个位数字对齐，且结果行中数字尽管相离较远，但是其单位名称是连续变化的，如上面开五次方的例题中，结果行中数字5位于百位，3位于十位，6位于个位;

(3)无论是哪一种开方运算，本质上是一种“增乘”的过程，对于印度数码的乘法运算可以进行心算，而六十进制数码的乘法运算需要借助于六十进制数码乘法表。尽管有这几点不同，但是本质上第1卷与第3卷中的两种算法是一致的。

下面我们来比较《算术之钥》与宋代贾宪增乘开方算法的异同:

两者的相同点都是在开方过程中采用随乘随加的机械化算法来构造减根方程，其算法核心是相同的。不同之处在于形式，主要有三点:

(1)与《算术之钥》相比，贾宪在算法的表述上过于“简略”，不过这也是中算传统中“寓理于算”的体现;卡西的表述十分详尽，对于从来没有接触过“增乘”开方的初学者很容易理解和掌握;同时为了便于表述，作者还引入了大量的术语，此部分内容置于书中开头的基础知识部分，更说明这种算法在当时早已有之，应当具有一定的流传广度;

(2)卡西将所有的开方过程体现在一张数表之上，在这点上不仅与中算不同，甚至与其早期的阿拉伯数学传统均不同，这在下文中还会继续讨论。正如卡西在述文中所说的那样，不同行中水平分割线表示其上方或下方的数字将要保留或是将要擦去，把所有的过程体现在一张数表上是便于初学者理解掌握和重现计算过程有利于检验运算的正确性，当然这是在纸张的普遍应用之后才可能实现的;

(3)最重要的一点，在中算“增乘”过程中算式排列的最下面一行是借算行，且每次求得的方根写在与被开方数数位相同的位置上;而卡西在算式排列的最下面一行为一次项行，即中算中的倒数第二行，没有借算行，且每次求得方根置于每一节的有理数位上，这些有理数位恰好是中算中“借算”所处的位置，即二者确定数位的作用是相同的。且在实际运算过程中卡西的数码排列方法反而会节省一行的空间。

事实上，12世纪的阿拉伯数学家萨马瓦尔就已经给出了与卡西相同的开高次方方法。萨马瓦尔在其印度算术书al-Qiwāmī中同样将按照闪语字母表顺序排列的阿拉伯字母表示数字进行高次开方，其书中的例题为:

求数字 0;0，0，2，33，43，3，43，36，48，8，16，52，30(30 的单位为 60－13)的平方立方根，解题过程的术文及数表如下①由于是对六十进制数码开方，故笔者认为下列数表(参考文献［3］)的排列顺序与原手稿的排列顺序恰好相反。:

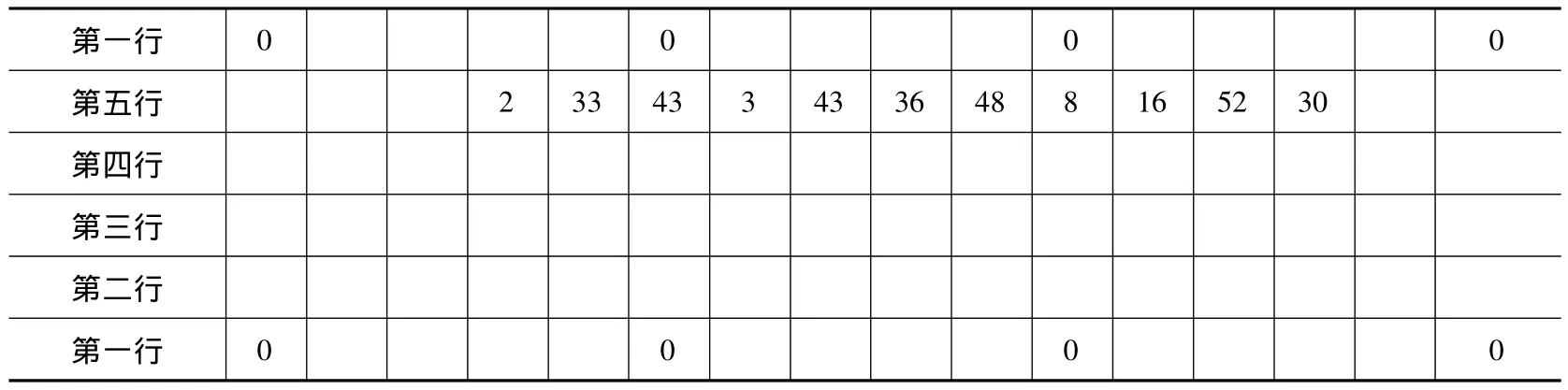
?第一行00023343343364881652300第五行第四行第三行第二行第一行0000

此时仔细观察最左侧有理数位上的数字，即度数位上的数字，其上为空位;随后移至下一位有理数位上的数字43，现找出一个最大数字，能将其平方立方从此位数字及其高位数字(共同构成的数字)中减去，得到6，将其写在最高和最低两行(的相应有理数位上);随后在六十进制数码乘法表中找出6(所对应的行)，用最高行数字乘以最低行数字，即6乘以6，将结果写在第二行;接下来将最高行数字(6)乘以第二行的结果，将结果加到第三行;随后将最高行数字(6)乘以第三行的结果，将结果加到第四行;最后将最高行数字与第四行数字的乘积从第五行(对应的数字)中减去，

得到下表:

?第一行0600第五行24734336488165230第四行2136第三行336第二行36第一行0600

一旦完成了十四步运算，并且把结果记录下来，那么这四行的运算便结束。(［3］，92～93页)

通过上面的叙述可以发现，这种算法应当是当时的数学家们频繁使用的，而不是萨马瓦尔的独创。幸运的是在手稿的前几页有一道关于求数字6五次幂的题目中萨马瓦尔详尽叙述了这“十四步”运算。在计算完数字6的连续次幂后，他给出了下面的术文及一张数表:

将右侧的数字6加到左侧，则左侧数字变为12;接下来将右侧的数字6乘以左侧的12，得到1，12，并将其加到第二行得到1，48;将右侧的数字6乘以第二行数字1，48，将结果加到第三行得到14，24;将右侧的数字6乘以第三行数字，并将结果加到第四行，得到1，48，0，此时最终得到第四行的数字。

将右侧数字6加到左侧得到18;将右侧数字6乘以左侧的18，得到1，48，随后加到第二行得到3，36;将右侧数字6乘以第二行数字3，36，将结果加到第三行，得到36，0，此时最终得到第三行数字。

将右侧数字6加到左侧数字18上，得到24;随后将右侧数字6乘以左侧数字24，并将结果加到第二行数字3，36上，得到6，0，此时最终得到第二行数字。

将右侧数字6加到左侧数字24上，最终得到30。(［3］，95页)

第一行 第二行 第三行 第四行 第五行 行①5thx1=6 x21=36 x31=3，36 x41=21，36 x51=2，9，3664th 2x1=123x21=1，484x31=14，245x41=1，48，03rd 3x1=186x21=3，3610x31=36，02nd 4x1=2410x21=6，01st 5x1=30

接下来，我们回到前面的开方过程，萨马瓦尔给出了如下数表(［3］，97页):

?第一行0600第五行24734336488165230第四行148第三行36第二行6第一行03000

随后萨马瓦尔指出通过移动四行中的数字得到新数表，如下所示(［3］，97页):

随后进行第二次估根，尽管相对于第一次估根要困难一些，但是萨马瓦尔没有进一步的评述，便得到数字12，并在同一页手稿中给出了下面两个数表(［3］，98～99页):

?第一行06120第五行11441394056165230第四行1552638294536第三行3713122848第二行66224第一行3012第一行06120第五行11441394056165230第四行23810448第三行39431648第二行62424第一行3100

不幸的是，手稿接下来的部分残缺了，通过前面的算法最终可以得到结果为:0;6，12，30。

从萨马瓦尔开方过程中算法原理、术语表述、数码排列的特点来看，卡西都很好地继承了早期阿拉伯数学家们的传统。主要的区别在于卡西将所有的开方过程整合到一张数表之中，萨马瓦尔给出了一系列分散的数表，这种算法显然适用于当时的土板算法;而从卡西的叙述来看，他恰好处于土板算法到纸张算法的过渡阶段。从现有史料来看，卡西《算术之钥》中关于开高次方的增乘算法更多的体现了早期的阿拉伯数学传统，并非受到中算直接的影响。接下来按照《算术之钥》的行文顺序讨论开方问题中无理根的近似算法。

2.2 高次开方中无理根的近似算法

在开方运算中并不是每一个被开方数都可以开尽。一般情况下，按照减根变换的方法求某整数的方根，运算至个位时如果在被开方数中有剩余数字，即此方根为不尽方根便产生了无理根的近似算法。中国早在《九章算术·少广章》开方术中就对此有论述，术文曰:

若开之不尽者，为不可开，当以面命之。

刘徽注文曰:

术或以借算加定法而命分者，虽粗相近，不可用也。凡开积为方，方之自乘当还复其积分，令不加借算而命分，则常微少;其加借算而命分，则又微多。其数不可得而定。故惟以面命之，为不失耳。［9］

在刘徽《详解九章算法》之后附录的《九章算法纂类》中关于贾宪开方术的术文中，均为“实除尽”的情形，对此没有说明。但是从宋元时期其他的相关著作来看，加“借算”这种传统始终存在，相当于若a=rn+t，则

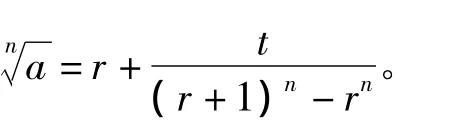
卡西在《算术之钥》第1卷第5章高次开方的一般方法之后给出了与中算类似的无理根近似算法:

如果有剩余数字，则此数为无理数，数行中的剩余数字为(方根中分数部分的)分子。而作为这个分数的传统近似分母应该是所得结果的开方次数的乘方与所得结果加一之和的开方次数的乘方之差。

随后按照上面的方法计算处理第一个有理数位上的数字(即将方根中的个位数字逐行增乘)，直至(将各行中的数字)移位(之前)，最后将数行之下各行中分隔线以上的数字之和再加一，此数恰为前面所要求的两个乘方之差，即传统分母。(［2］，67页)

卡西按照此方法处理上述五次开方问题的结果，他将最后各层中分隔线以上的数字重新列表，以及运算的分数结果如下所示①见参考文献［2］，71页。笔者仅将数表中的阿拉伯文及东阿拉伯数码进行翻译，数表的排列顺序未作修改。:

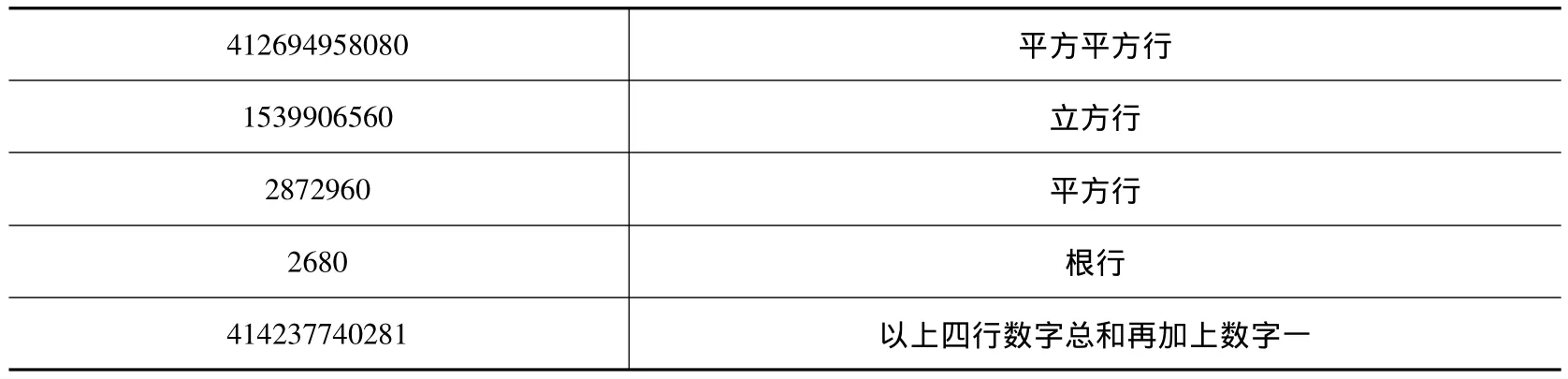
最后得到方根的结果，如下所示:

536

21

414237740281①卡西在《算术之钥》中表示分数时，如果有整数部分，则将其写在最上面一行，以下依次为分子和分母;整数为零时，有时被省略。则上述结果相当于:

显然卡西的这种不尽方根的近似算法与刘徽注中加“借算”的方法完全相同，只不过此时卡西已将其运用到任意高次幂。此外卡西明确指出这个分数的分母是“所得方根的开方次数的乘方与方根加一之和的同次数乘方之差”，这里面有三层含义:第一，卡西认为开分运算的本质就是求两个连续乘方的差;第二，上述的增乘算法恰好可以构造出这两个连续乘方之差;第三，这种近似算法的原理是进行线性插值。

我们注意卡西在术文中将加“借算”的分母称为“传统分母”，说明此法早已有之。R.Rashed指出，事实上这种不太精确的近似方法在凯拉吉和萨马瓦尔之前的阿拉伯数学家中使用较为普遍，他们仅将这种近似算法局限在求三次方根以内。例如乌格里迪西(al-Uqlidisi，约920～约980)就在其书中对于开平方运算给出过加“借算”的近似算法，即若:N=a2+r，则有:;阿尔·巴格达第(al-Baghdadi，约980～1037)将此近似算法应用于开立方运算，即若:N=a3+r，则有:［3］，109 ～110页)。

到了萨马瓦尔时，已将此算法应用于任意次幂的开方近似运算中。在萨马瓦尔的印度算术著作al-Qiwāmī中，紧接着“增乘”算法后面，对于无理根的近似算法，他指出:

要求某数的平方根、立方根或是任意次方根，当得到了方根的整数部分…如果此时(被开方数)有剩余…现要得到一个较为精确的方根，则需将剩余的数字作为分子，将此开方次数下的系数乘以所得方根整数的不同次数的乘方，最后将所得的数字之和加1，此即为近似方根分数部分中的分母。(［3］，134页)

所以这就可能是为什么其后的阿拉伯数学家，如纳西尔·丁·图西(Nasir al-Din al-Tusi，1201～1274)及卡西在其各自的书中均将此加“借算”的分母称为“传统分母10”。显然无论是中算家还是阿拉伯数学家都无法满足于这种精度的不尽方根，因此产生了更为精确的近似算法。刘徽在《九章算术注》中曰:

不以面命之，加定法如前，求其微数，微数无名者以为分子，其一退以十为母，其再退以百为母。退之弥下，其分弥细，则朱幂随有所弃之数，不足言之也。

此处的“微数”，按照郭书春先生的观点指的是细微的数，即按照上述的开方程序，求既定的名数以下的部分。实际上是以十进制分数逼近无理根。(［9］，138页)

在《算术之钥》中也有类似的表述，只不过卡西不像刘徽那样一口气全盘托出，而是在上述的近似算法之后指出:

还有一种求无理乘方比较精确方根的方法，我们将其安排在下一章，因为这涉及

到分数的相关知识。(［2］，73页)

卡西将第二种相对更为精确的方法安排在第2卷中的分数开方部分。下面来看两种文明对于处理分数开方问题的相关内容。

在中算里，这点同样可以追溯到《九章算术·少广章》，术文曰:

若实有分者，通分内子为定实，乃开之。讫，开其母，报除。若母不可开者，又以母乘定实，乃开之。讫，令如母而一。(［9］，133页)

贾宪立成释锁平方法曰:

积有分子者，以分母乘其全，入内子，又以分母再自乘之，开平方，求积，如分母自乘而一。(［7］，260页)

在《算术之钥》第2卷第10章分数开方部分中，卡西给出了如下四种类型(［2］，95～96页):

(1)对于分子分母都是有理数的分数开方问题，用分子的方根除以分母的方根;

(2)但如果二者均没有精确的方根，对于平方根，用分子乘以分母一次;求立方根，乘两次;求平方平方根，乘三次;求平方立方根，乘四次，以此类推。随后求出最后乘积的一个近似方根，并除以原来分数的分母，此即为所求;

(3)如果分数中带有整数，则可以按照前一卷中的算法，首先求出整数部分的方根大小，剩余的整数和分数一起作为传统分母的分子，随后如前化简;

(4)将整数部分化为分数中的分子，然后按照前面的方法取其方根。

卡西所给的分数开方方法本质上与中算中的方法相同，不过卡西已经将其推广到任意高次幂的情况且更加系统化。接下来卡西给出了另一种类似《九章算术》刘徽注中“微数”算法相同的表述:

我们知道将任意一个数乘以某数(开方次数)的乘方，随后取乘积的方根，再除以此数，则所得的结果比直接开方的结果更为精确，且所乘的乘方越大，结果越精确。因此对于任意的被开方数，在开平方时可以乘以100;在开立方时乘以1000;在开平方或者平方平方时均可以乘以10000……在数字的右边要额外加上一些数字0，如果是开平方则加上两个0;如果是开立方，则加上三个0;如果是开平方平方，则要加上四个0。其中开方的次数应当为被开方数右侧所增加0数目的约数，且增加数目越多，结果就越精确。随后将表格中加上0之后的数字开方，将所得的方根除以前面所乘乘方的方根，而在实际运算中仅需要将原来被开方数字上方结果行中的数字视为(结果中的)整数部分，随后用所增加0上面的结果乘以传统分母，再将此乘积加上被开方数中剩余的数字。将得到的结果写在前面整数的下方作为分子，在传统分母的右侧要加上数字0，其个数等于被开方数中增加0的上方结果行中所增加的数字位数，即乘方中由于0的增加所增加方根数的位数;或者按照若求平方根，则将增加0的个数取半;若求立方根，则取增加0的个数的三分之一;若求平方平方根，则取增加0的个数的四分之一，将其作为分母，最后如果分子分母中有公约数的话还要将其约去。(［2］，97页)

卡西给出的例题是求145的平方根:

例题:现要求145的平方根，同前面一样首先绘制表格，在结果行中得到数字十二，此时被开方数中剩余数字一，则其为无理数。

如果要求出更加精确的结果，则需要在数字的右边加上偶数个零，此处加上四个0，并且为它们额外画出四列，用另一种颜色加以区分，如下所示:

2 2461638440048①12041450000121

在被开方数上方的结果行中得到十二，将其作为结果中的整数部分;用数行中后来所增加数字0上方的数字，即4乘以传统分母，即2409得到9636;随后将其加上数行中剩余的数字，即384，得到10020，将其写在分子的位置;随后在传统分母的右侧

同样也可以将增加的数字0上方结果作为(最后方根的)分子部分，但是此时的分母为原来被开方数所乘乘方的方根，即在数字1的右侧增加几个0，其个数等于结

果行中位于被开方数中增加的0上方所增加的数位位数。但是这样得到的结果不如上面例题方法得到的结果精确。(［2］，98页)

上文主要内容恰好是中算里的“微数”算法，相当于，这种方法在阿拉伯被称为“零算法”。从9世纪开始，就有多位阿拉伯数学家开始使用这种方法来逼近无理平方根、立方根。例如与花拉子米同时代的Banu Musa(约805～873)就给的运算表达式;乌格里迪西在其952年的著作al-Fusul中利用此法进行开平方和开立方;巴格达第在其著作al-Takmila中利用此法进行开立方，直至萨马瓦尔才在其1172年的著作《印度算术》中将其扩展到开任意次幂，其方法与卡西相同(［10］，383页)。

综上所述，卡西对于不尽方根的近似算法保留了早期的阿拉伯数学传统，但此时已经更趋于系统化、理论化，且卡西在进行无理根近似运算时，为了得到更为精确的结果，是将“线性插值”与“微数”算法同时使用。

随后我们继续回到第一卷，卡西接着叙述道:

如果利用上述数字排列的方法计算更高(的精度)，尤其是在被开方数数位较多以及开方次数较大的情况下则比较困难。我们已经在其他文章中介绍过另外一种方法。(［2］，73 页)

虽然卡西此处并没有明确说明“其他文章”中的“另外一种算法”指的是什么，而且在《算术之钥》也没有给出其他的不尽方根近似算法，但是在《算术之钥》中的众多数表里的无理方根都达到了相当高的精度，对于这些笔者认为卡西指的可能是类似《论圆周》推算圆周率时使用的加速逼近算法，这点还有待于进一步的研究。但是上述近似算法作为数学知识的基础部分对于普通的学生已经足够了。

无论是贾宪还是卡西在开方问题中除了增乘开方法以外，还给出了立成释锁开方法及与其有密切关系的算术三角形，下面来分析二者的异同。出过形如

2.3 “立成释锁”开方法与算术三角形

贾宪给出增乘开方法后，接下来给出了“立成释锁”开平方法和“立成释锁”开立方法，钱宝琮先生认为:

立成释锁开方法…演算步骤大致和《九章算术·少广章》相同。“释锁”是宋元数学家开方或解数字方程的代用名词。唐代以后天文学家为预推各项天文数据立出来的表叫做“立成”。因此，贾宪的立成释锁法可以解释作:利用一种表格上的数字来解决一般的开方问题。这种数字表格很可能就是他提出的指数为正整数的二项式定理系数表——“开方作法本源”。开平方和开立方用着这个系数表的第三层和第四层。如果推广到求四次幂、五次幂或六次幂的根时，就要用到第五、第六或第七层了。(［4］，37～38页)

“开方作法本源”图，即算术三角形，首见于明《永乐大典》第16344卷第5页“杨辉详解开方作法本源，出《释锁算书》，贾宪用此术”。后来元代朱世杰《四元玉鉴》载有“古法七乘方图”，比前者多两层且加了斜线。明吴敬《九章比类》亦载有添加了斜线的五层图。明王文素将前人按照等腰三角形形状排列的系数三角形改为按照直角三角形排列，取名“开方本源图”，载于其《算学宝鉴》(1524)中。

在卡西的《算术之钥》中增乘开方法之后，同样也给出了立成开方法与算术三角形，术文如下:

另一种方法:

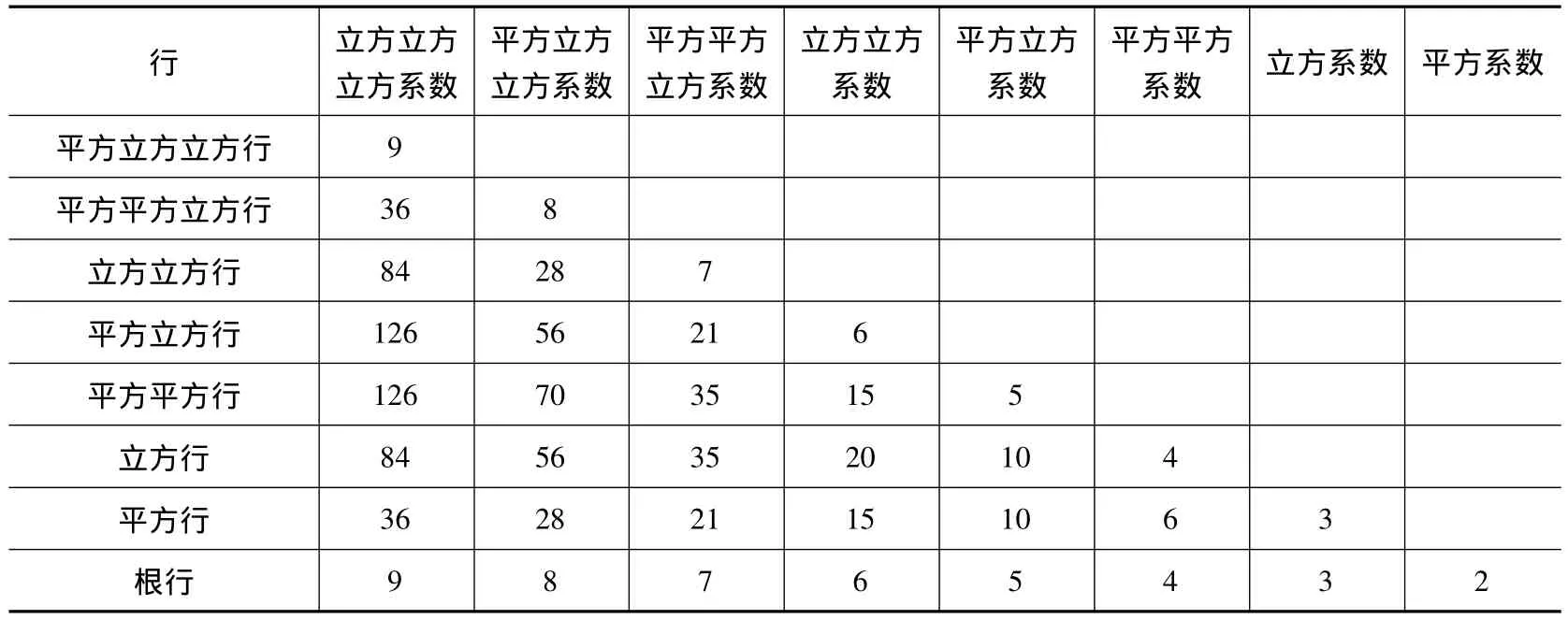
如果要求两个乘方之差，便需要知道在此开方次数下的各项系数。这些系数实际上就是当结果行中的数字为1时，按照前面的(增乘)算法在每次移项之前位于各行中的数字。

例如:现要求平方立方的各项系数，如前所述做出表格，在结果行中写出数字1，在根行中同样如此。按照上面的(增乘)算法，在移项之前得到根行的数字为5，平方行中为10，立方行中为10，平方平方行为5。

此时得到的四个数字便是平方立方的各项系数，其中每一个数字(对应的乘方)次数与其所在行名称相同。在求平方立方根过程中每次移项时所移动的数字实际上就是刚才得到的系数与结果行中的数字及其乘方的乘积。

?15411064311046332154321结果行平方平方行立方行平方行根行

例如用结果行中的数字乘以移位之前根行中的数字5，再用结果行中数字的平方乘以平方行中的数字10，用其立方乘以立方行中的数字10，用其平方平方乘以平方平方行中的数字5，随后将这些数字之和加1，即为结果行中数字的平方立方与其加1后所得和的平方立方之差。

通过计算得到平方的系数只有一个，即为2;立方的系数分别为3、3;对于此后次数每增加一次，其系数的个数就增加一个。其中系数两端的数字依次增加(1)。将某次数下任意相邻的两个系数相加，所得便是相邻下一个次数中中间一项的系数。(［2］，72～75页)

随后卡西给出了算术三角形①见参考文献［2］，74页.笔者仅对数表中的阿拉伯文及东阿拉伯数码进行翻译，并未改变数表的排列顺序。，并给出了利用算术三角形求两个连续乘方之差的一般方法，最后给出了两道例题，分别为:55－45、75－45，且附有演算数表。

以上便是《算术之钥》开方问题的全部内容。

杜石然先生曾指出:

除高次开方法外，阿尔·卡西《算术之钥》中还引入了一个二项式定理系数表。阿尔·卡西曾利用这一数表来计算相邻或者不相邻两自然数的同次幂之差，例如书中所举的例题:求55－45或75－45等等…值得注意的是卡西关于求出二项定理系数表中各数的方法，也和贾宪“求廉草”中所用的方法完全相同。(［7］，259页)

阅读原文便可以发现，上述认识有两处不妥:其一、卡西认为开方问题的本质就是求两个连续乘方之差，而利用算术三角形求两个连续乘方之差是一种开方方法，而不仅仅是计算“相邻或不相邻两自然数的同次幂之差”问题;其二、贾宪与卡西所给出的算术三角形在形式和构造上不同。在形式上前者比后者每一行多出了两端的数字1，其中一个恰好是中算中“立成释锁”开方法与“增乘开方法”在算筹布式中的“借算”;而卡西的算术三角形中没有两端的系数1，这恰好也与其没有“借算”行的特点相吻合。另外中算中的算术三角形起初采用等腰三角形的形式排列，这就需要将每行中的系数应用于每列中进行立成算法，虽然并不实用，但却体现了中算家追其一种形式上的统一性与完美性。与中算不同，卡西的算术三角形采用直角三角形的形状排列，且与其在开方过程中的数字排列顺序完全一致。最后卡西给出了两种构造算术三角形的方法，其中一种与贾宪“求廉草”法相同，另一种是利用各行系数间的关系，即来求得。从术文来看卡西对于算术三角形中各行数字间的关系已经很熟悉，可以判断算术三角形应早已有之，后面会继续讨论阿拉伯数学史中算术三角形的内容。尽管卡西给出的第二种开方方法与贾宪所述的立成释锁方法相同，且同样利用增乘开方法构造出了算术三角形，但仅凭这些就来推断二者之间的相互影响是不够的。

事实上萨马瓦尔在al－Qiwāmī中介绍完增乘开方法后，与《算术之钥》相同紧接着给出立成算法，其中详述了二、三、四、五次开方问题的立成算法，下面以求五次方根为例进行说明:

若求250的平方立方根(即五次方根)，得到3，剩余7，由于五次方的系数为5、10、10、5，将方根中的整数3乘以第一个系数;3的平方乘以第二个系数;3的立方乘以第三个系数;3的平方平方(即四次方)乘以第四个系数，将这几个乘积之和加上数字1，得到781，此即为(被开方数中)剩余数字的分母。最后得到3又781分之7。如此继续运算其余(更高)次幂的方根。(［3］，136页)

由卡西与萨马瓦尔对于立成开方法的描述可以看出，二者在方法、编写顺序，甚至是语言的细节上都有众多相似之处。究竟萨马瓦尔是否影响了卡西，还有待于进一步研究，但至少在立成方法上，卡西保持了十二世纪的阿拉伯数学传统。

另外与贾宪立成开平方法及开立方法相比，萨马瓦尔和卡西除了将其推广到任意高次幂这点不同以外，两种文明对于增乘与立成的关系认识也不同。“增乘”与“立成”两种算法名称源于中算，形成于由传统的开平方、开立方向高次开方机械化算法发展的过渡阶段。贾宪先给出立成释锁开方法，后给出增乘开方法，虽未给出二者的关系，但是很明显前者是在《九章算术》开方术基础上演化而来，属于算法的初级阶段;而“增乘”算法对于高次开方问题在利用算筹计算时体现了较强的机械性和可操作性，从认知的先后顺序来看，后者应该为前者发展的高级阶段。后增乘开方法经刘益、秦九韶、李冶、朱世杰等人的发展，在高次方程数值解领域取得了辉煌的成就。中国数学史界传统的观点认为到了明代，增乘开方法已经失传，在王文素的《算学宝鉴》中的高次开方问题全部采用的是立成释锁开方法，且运算方法已经由珠算取代了筹算。笔者认为可能增乘开方法并未消失，只不过由于珠算的迅速发展，使得高次开方问题可以全部统一为立成释锁开方法。由于中算史料相对的零散性以及两种算法各自的优缺点，或许在不同的发展阶段中算家对其关系的认识不同，这点有待于进一步的研究。而萨马瓦尔和卡西却先给出增乘算法，随后给出立成算法，虽然将二者称为两种方法，但是并没有割断二者之间本质的联系。且从书中例题可以看出对于被开方数相对于开方次数不大的情况下采用一次立成算法即可开方结束，体现了阿拉伯数学家运算灵活不拘于形式的特点。此外，通过立成算法，可以将增乘算法与算术三角形之间建立联系，同时算术三角形揭示出增乘算法的构造原理并将三者有机的统一起来。下面来讨论一下有关算术三角形的问题。

事实上在萨马瓦尔的著作［11］中就有关于算术三角形的论述，这是至今所知在阿拉伯数学史中最早的关于算术三角形的记载，而萨马瓦尔又是在转述10世纪阿拉伯数学家凯拉吉的成果。萨马瓦尔在书中是在利用不完全数学归纳法推算公式的 过程中得出算术三角形，随后根据推导过程构造算术三角形并阐述了其构造过程，相当于，算术三角形数表如下所示(［11］，111 页):

?立方立方立方 立方 立方 立方 立方 立方立方 立方 立方1111111111112111098765432665545362821151063122016512084563520104149533021012670351551792462252126562161924462210842871792330120368149516545912205510166111121平方立方平方平方立方立方平方立方平方平方立方立方平方立方平方平方立方 平方 物111

卡西给出的算术三角形同上面的数表相比，缺少两侧的系数“1”，但这恰好满足其“增乘”开方没有“借算”行的特点。除此之外，卡西继承了上述数表的直角三角形排列、表头名称、系数构造原理等多个特点。从现有史料来看中算家和阿拉伯数学家几乎在同时认识到了算术三角形，但是认识的途径、目的和意义均是不同的。

3 “盈不足”术与“契丹”算法

“盈不足”术是中国古代的一种比较古老的著名算法，早在《九章算术·盈不足》中就有记载。杜石然先生曾指出:从公元10世纪开始，阿拉伯数学家就开始用“hisab al-khataayn”这一名称来表示盈不足术，直至《算术之钥》的第5卷第2章中仍然以此作为标题。此外杜石然先生也倾向于钱宝琮先生的观点，即:al-khataayn是由“契丹”一词的音译转化而成(［7］，248～251页)。

在《算术之钥》第5卷中卡西将还原与对消、al-khataayn算法和分析综合法作为解决代数方程的三种常用方法。因为这种算法在阿拉伯早已有之，所以很难从《算术之钥》的内容上确定其早期的是否受到中算的影响。笔者此处仅就al-khataayn的阿拉伯语进行语义上的分析。

《算术之钥》第5卷的标题为

译为:通过还原与对消及双假设等方法来求解未知数;

4 结论

综上所述，就《算术之钥》与中算相似问题，尤其是高次开方问题所涉及的一系列相关算法内容来看，二者在论述、方法等方面都有显著的不同;且纵观阿拉伯数学史，对于这些不同点，卡西都保留着10至12世纪的阿拉伯数学传统，可以判断《算术之钥》中的这些问题并没有像传统观点所认为的那样受到中国宋元数学的直接影响，不过这恰好体现了早期文明中数学发展多元化的特点。至于中阿间的数学交流，还有待于更多史料的解读和研究。

笔者在本文的书写过程中发现以下几个问题值得认真思考并可以成为后续的研究方向:

1.阿拉伯原始文献中数学语言的来源、演化及其准确的翻译方式;

2.阿拉伯数学史中十进制数码与六十进制数码间的算术运算关系;

3.卡西对于无理方根的所有逼近算法及其来源与演化;

4.通过卡西《算术之钥》中第5卷代数学部分与萨马瓦尔《代数珍宝》之间的比较研究来进一步剖析12至15世纪阿拉伯数学史晚期代数学的发展概况。

此外笔者认为在现阶段，由于史料研究的不足，对于早期跨文明数学史的比较研究，一些启发性研究工作的价值要大于某些结论;尤其是在对待“起源”、“谁影响了谁”这类问题时，应当慎重对待。鉴于笔者水平有限，文中的错误和不妥之处还请专家读者批评指正。

1 B A Rosenfeld.A P Youschkevitch.Biography in Dictionary of Scientific Biography［M］.New York:Charles Scribner's Sons，1970～1990.255～262.

2 Jamshīd al-Kāshī.Miftāh al-Hisāb(Key to Arithmetic)［M］.A S al-Demerdash.M H al-Cheikh(eds).Cairo:Dār alkātib al-‘arabī，1967.

3 Rashed R.The Development of Arabic Mathematics:Between Arithmetic and Algebra［M］.A FW Armstrong(trans).Norwell:Kluwer Academic Publishers，1994.

4 钱宝琮.增乘开方法的历史发展［A］//钱宝琮.宋元数学史论文集［C］.北京:科学出版社，1966.36～44.

5 Luckey P.Die Ausziehung desn-ten Wurzel und der binomische Lehrsatz in der islamischen Mathemarik［M］.Springer:Math Annalen 120，1948.217 ～274.

6 Dakhel A K.The Extraction of the n-th root in the sexagesimal notation，a study of chapter5，treatise IIIof by Jamshīd Ghiyāth al-Dīn al-Kāshīwith translation and commentatry［D］.WasfīA Hijab.E SKemmedy(eds).Beirut:American University，1960.

7 杜石然.试论宋元时期中国和伊斯兰国家间的数学交流［M］//钱宝琮.宋元数学史论文集.北京:科学出版社，1966.258.

8 杜石然.再论中国与阿拉伯国家间的数学交流［J］.自然科学史研究，1984，3(4):294～303.

9 郭书春.九章算术译注［M］.上海:上海古籍出版社，2007.133.

10 Rashed R.Combinatorial analysis，numerical analysis，Diophantine analysis and number theory［M］//R Rashed:Encyclopedia of the History of Arabic Science.New York:Routledge，1996.383.

11 Al-Samaw'al.al-Bahir en algebra［M］.SAhmd.R Rashed(eds).Damascus∶Imp.De I'Universite de Damas，1972.