基于LMD和Lempel-Ziv指标的滚动轴承故障损伤程度研究

张 超，陈建军

(1.内蒙古科技大学 信息工程学院，包头 014010;2.西安电子科技大学 机电工程学院，西安 710071)

基于LMD和Lempel-Ziv指标的滚动轴承故障损伤程度研究

张 超1，2，陈建军2

(1.内蒙古科技大学 信息工程学院，包头 014010;2.西安电子科技大学 机电工程学院，西安 710071)

针对不同转速下，不同损伤程度的滚动轴承内、外圈故障，提出一种基于局域均值分解(Local Mean Decomposition，LMD)和Lempel－Ziv指标的滚动轴承损伤程度识别方法。LMD方法是一种新的自适应时频分析方法，将轴承振动信号分解为若干个瞬时频率有物理意义的乘积函数(Production Function，PF)，再结合峭度条件找出蕴含故障信息的最优PF分量，计算其PF函数和包络的Lempel－Ziv的归一化值，再加权求和得到最终的Lempel－Ziv综合指标，表征了不同故障的损伤程度。同时还研究了在不同转速下的内、外圈故障轴承的Lempel－Ziv指标的分布规律，使结论更具有普遍性。经实验结果验证，此方法能有效地应用于滚动轴承的故障程度的诊断。

局域均值分解;Lempel－Ziv指标;损伤程度;乘积函数;故障诊断

轴承是各种旋转机械中应用最广泛的一种通用机械部件，机械设备运行时，磨损、疲劳、腐蚀、过载等原因都可能造成轴承的局部损伤。一个微小的故障，可能会影响到整个系统运行的稳定性和安全性，甚至造成灾难性后果，因此对轴承的状态检测和故障诊断具有重要的现实意义。

传统的故障诊断方法是通过对故障振动信号进行时域和频域分析，进行轴承工作状态的辨识［1－3］。然而，由于负载、摩擦、间隙和刚度等非线性因素对振动信号的不同影响，仅在时域和频域对齿轮、轴承工作状态进行精确诊断是比较困难的［4］。如何从非平稳的振动信号中提取出故障特征信息是故障诊断的关键［5］。文献［6］提出了基于EMD和Lempel－Ziv指标的滚动轴承损伤程度识别研究，它提出一种归一化的Lempel－Ziv复杂度指标用于滚动轴承状态恶化的评估，讨论了故障大小与信号非线性之间的关系。但是没有讨论不同转速情况下该方法的有效性。

Smith［7］提出一种新的自适应时频分析方法－局域均值分解方法(Local Mean Decomposition，LMD)，并将这种方法应用于脑电图的信号处理。LMD方法将一个复杂的多分量信号分解为若干个瞬时频率有物理意义的乘积函数，其中每一个PF分量由一个包络信号和一个纯调频信号相乘得到。

本文针对不同转速下，不同损伤程度的滚动轴承内、外圈故障，提出一种基于LMD和 Lempel－Ziv指标的滚动轴承损伤程度识别方法。首先，将轴承振动信号应用LMD分解为若干个瞬时频率有物理意义的乘积函数，再结合峭度条件找出蕴含故障信息的最优PF分量，计算此PF函数和其包络的Lempel－Ziv的归一化值，再加权求和得到最终的Lempel－Ziv综合指标，进而表征了不同故障的损伤程度。同时还研究了在不同转速下的内、外圈故障轴承的Lempel－Ziv指标的分布规律，使结论更具有普遍性。经实验结果验证，此方法能有效地应用于滚动轴承的故障程度的诊断。

1 局域均值分解

1.1 LMD算法

LMD方法本质上是从原始信号中分离出纯调频信号和包络信号，将纯调频信号和包络信号相乘便可以得到一个瞬时频率具有物理意义的PF分量，循环处理至所有的PF分量分离出来，便可以得到原始信号的时频分布。对于任意信号x(t)，其分解过程［7－8］如下。

(1)确定原始信号x(t)所有的局部极值点ni，计算相邻两个极值点ni和ni+1的平均值mi，即：

将所有相邻两个极值点的平均值mi用折线连接，然后采用滑动平均方法进行平滑处理，得到局部均值函数m11(t)。

(2)采用局部极值点ni计算包络估计值αi：

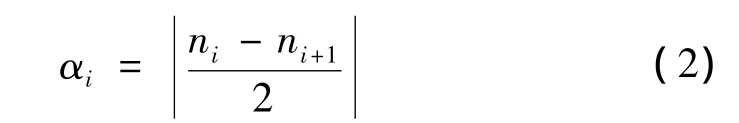
同样，将所有相邻两个包络估计值αi用折线连接，然后采用滑动平均方法进行平滑处理，得到包络估计函数α11(t)。

(3)将局部均值函数m11(t)从原始信号x(t)中分离出来，得到：

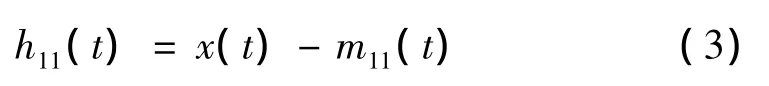
(4)用 h11(t)除以包络估计函数 α11(t)以对h11(t)进行解调，得到：

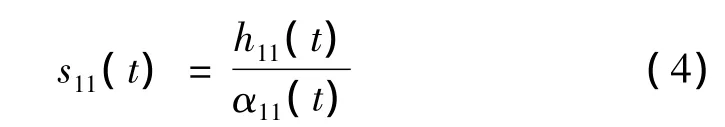
理想地，s11(t)是一个纯调频信号，即它的包络估计函数α12(t)满足α12(t)=1。如果s11(t)不满足该条件，则将s11(t)作为原始数据重复以上迭代过程，到得到一个纯调频信号s1n(t)，即s1n(t)满足－1≤s1n(t)≤1，它的包络估计函数 α1(n+1)(t)满足 α1(n+1)(t)=1。因此，有：

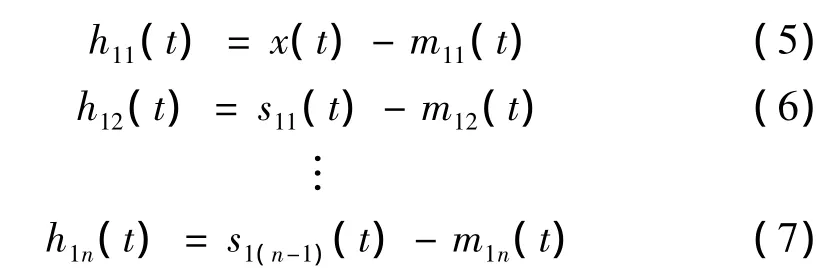
在实际应用中，可以设定一个变动量Δ，当满足时1－Δ≤α1n(t)≤1+Δ时，迭代终止。

(5)把迭代过程中产生的所有包络估计函数相乘便可以得到包络信号(瞬时幅值函数)：

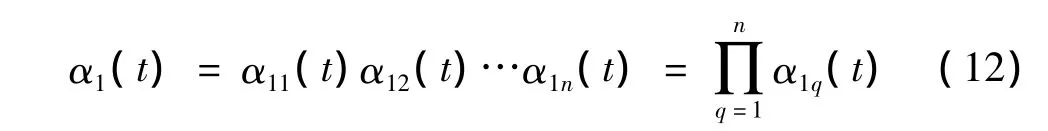
(6)将包络信号α1(t)和纯调频信号s1n(t)相乘便可以得到原始信号的第1个PF分量：

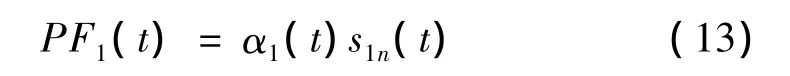
它包含了原始信号中最高的频率成分，是一个单分量的调幅－调频信号，其瞬时幅值就是包络信号α1(t)，其瞬时频率f1(t)则可由纯调频信号s1n(t)求出，即：

(7)将第1个PF分量PF1从原始信号x(t)中分离出来，得到一个新的信号u1(t)，将u1(t)作为原始数据重复以上步骤，循环k次，直到uk(t)为一个单调函数为止。

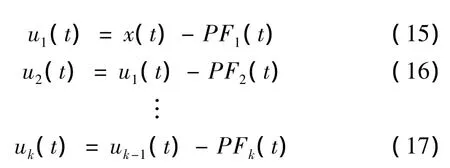
至此，将原始信号x(t)分解为k个PF分量和一个单调函数uk(t)之和，即：

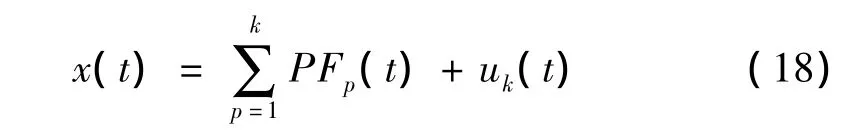
将所有PF分量的瞬时幅值和瞬时频率组合便可以得到原始信号x(t)完整的时频分布。

1.2 信号仿真

下面以一个具体的例子来说明LMD分析方法和过程，仿真信号为：

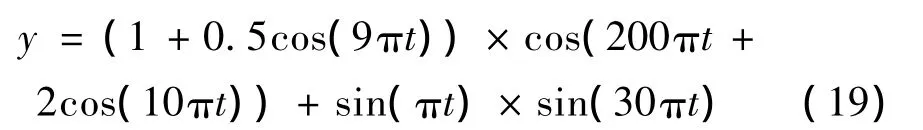
图1为LMD分解结果，原始信号被分解成2个PF和一个残余分量R，最先分解得到的PF1频率最高，PF1至PF2频率逐渐降低，残余项的幅值比较小，对后续分析的影响很小。

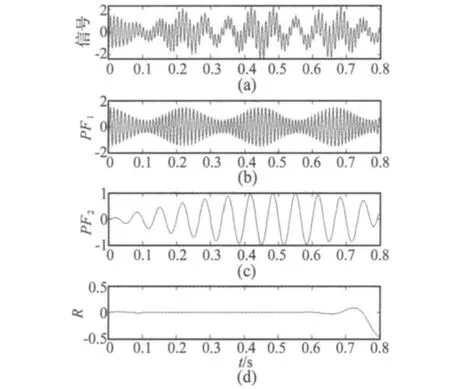
图1 仿真信号LMD分解结果Fig.1 LMD decomposition results of simulation signal

2 峭度指标和Lempel-Ziv复杂度

2.1 峭度指标

峭度(Kurtosis)K是反映振动信号分布特性的数值统计量，是归一化的4阶中心矩［9］：

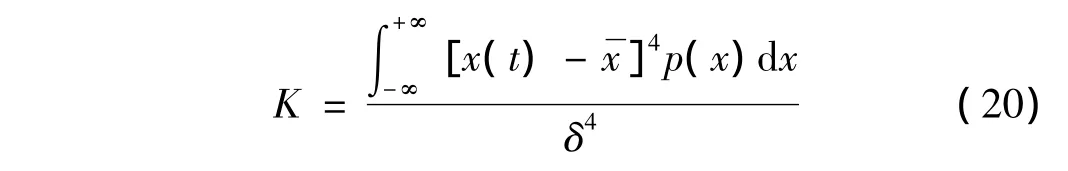
对于一组给定的离散振动信号数据，其峭度系数K为：

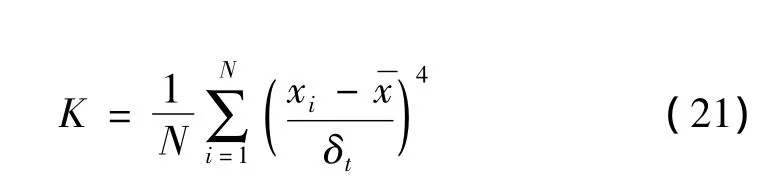
式中：xi为信号值;为信号均值;N为采样长度;δi为标准差。

峭度是表示轴承工作表面出现疲劳故障时，每转一周，工作面缺陷处产生的冲击脉冲，故障越大，冲击响应幅值越大，故障现象越明显。峭度是无量纲参数，由于它与轴承转速、尺寸、载荷等无关，对冲击信号特别敏感，特别适用于表面损伤类故障、尤其是早期故障的诊断。在轴承无故障运转时，由于各种不确定因素的影响，振动信号的幅值分布接近正态分布，峭度值K≈3;随着故障的出现和发展，振动信号中大幅值的概率密度增加，信号幅值的分布偏离正态分布，正态曲线出现偏斜或分散，峭度值也随之增大。峭度指标的绝对值越大，说明轴承越偏离其正常状态，故障越严重，如当其值K＞8时，则很可能出现了较大的故障。故可以将峭度指标的大小作为选取PF分量的依据，找到最优分析对象。分别求取LMD分解所得的PF分量的峭度指标，选取峭度最大的PF分量作为研究对象，求其Lempel－Ziv 复杂度。

2.2 Lempel－Ziv 复杂度

Lempel－Ziv指标［10］是衡量有限时间序列复杂度的有力工具。Lempel和Ziv介绍了一种简单的计算方法，采用有限序列两个基本过程：复制和插入。考察序列 SN={s1，s2，…，sN}，则 SN的 Lempel－Ziv 值可按CN(r)(r≤N)，通过 N 次循环计算，步骤如下［6］：

(1)初始：Sv，0={}，Q0={}，CN(0)=0，r=0，令 Qr={Qr－1Sr}，由于 Qr不属于 Sv，r－1，则：CN(r)=CN(r－1)+1，Qr={}，r=r+1;

(2)令 Qr={Qr－1Sr}，判断 Qr是否属于 Sv，r－1={Sv，r－2Sr－1}，若是，则：CN(r)=CN(r－ 1)，r=r+1，重复步骤(2);

(3)若否，则：CN(r)=CN(r－1)+1，Qr={}，r=r+1，重复步骤(2)。

即序列SN的Lempel－Ziv值为5。

其中，样本复杂度与样本大小有关，即CN(N)的值受SN长度N影响明显。为了得到一个相对独立的指标，Lempel和Ziv进一步提出了如下的归一化公式［10］：

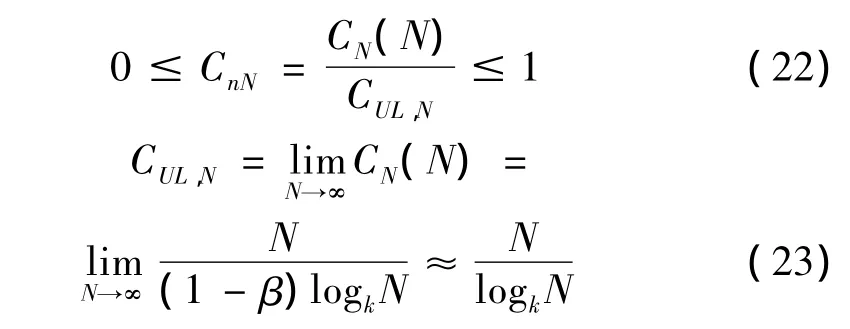
则，通过以上两个公式可以定义Lempel－Ziv的归一化公式为：

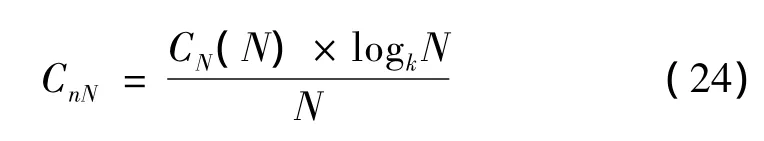
其中：k为SN中元素的个数(对于二进制序列SN，k=2)。当N值足够大时，式(22)成立。文献［11］给出了N的经验取值N≥3 600。称CnN为Lempel－Ziv归一化指标。

3 基于LMD和Lempel-Ziv指标的故障诊断步骤

基于LMD和Lempel－Ziv指标的轴承故障诊断步骤如图2所示。

使用LMD算法对原始轴承振动信号进行分解得到瞬时频率具有物理意义的PF分量;然后利用峭度(式(21))求取各个PF分量的峭度值，从中找出峭度值最大的PF分量，即最优的PF分量，它蕴含最准确的故障信息且信噪比最高;对PF分量和包络进行二值化处理。

二值化［12］的一般方法是先求出该段时间序列的平均值，再以该均值为界。把所有小于或等于该均值的幅值都置为0，而把所有大于该均值的幅值都置为1，从而把待处理的PF分量转化为以0和1两个字母构成的0、1序列。从原理上讲，数据经二值化处理后，信息有所丢失。新得到的二值化0、1序列主要反映了原信号以均值为中心的交变特性。细节上的变化情况在新序列中得不到反映。但若忽略信号的细节部分而从总体上考察信号的交变特性，也能在一定程度上衡量信号的复杂程度。经过实验数据验证，二值化处理后所计算的复杂度在许多场合能一定程度地反映原信号的复杂程度。对大量的试验数据分别进行二值化、四值化和八值化处理，计算其复杂度，发现三者的总体变化趋势基本一样。经过二值化处理后的信号与原始信号相对比，信号的频谱和信号所携带的能量会略有改变，但是Lempel－Ziv复杂度算法中的二值化方法只是在对复杂信号做复杂度测试前进行的粗粒化处理中的一种手段。实验结果表明，可以只关心原始信号以均值为中心的交变特性，就能够计算出Lempel－Ziv归一化值，从而能准确判断出机械部件的损伤程度。因此，经过二值化处理后信号其他方面的变化就不做考虑了。

分别计算PF分量及其包络的Lempel－Ziv归一化值CnNH和CnNL，其中，CnNH和CnNL分别代表高频载波与低频调制波对复杂度的主要影响，再综合得到最终指标 CnNF，称之为 Lempel－Ziv综合指标：CnNF=wh×CnNH+wl×CnNL(25)式中：wh为高频载波的权值系数，wl为低频调制波的权值系数。文献［6］指出，由于内、外圈故障信号组成成分的差异，权值系数wh和wl的经验取值也有所区别。对于内圈损伤wh=1/3，wl=2/3;对于外圈损伤wh=1/2，wl=1/2。最后，可以根据 Lempel－Ziv 综合指标判断轴承振动信号的损伤程度。

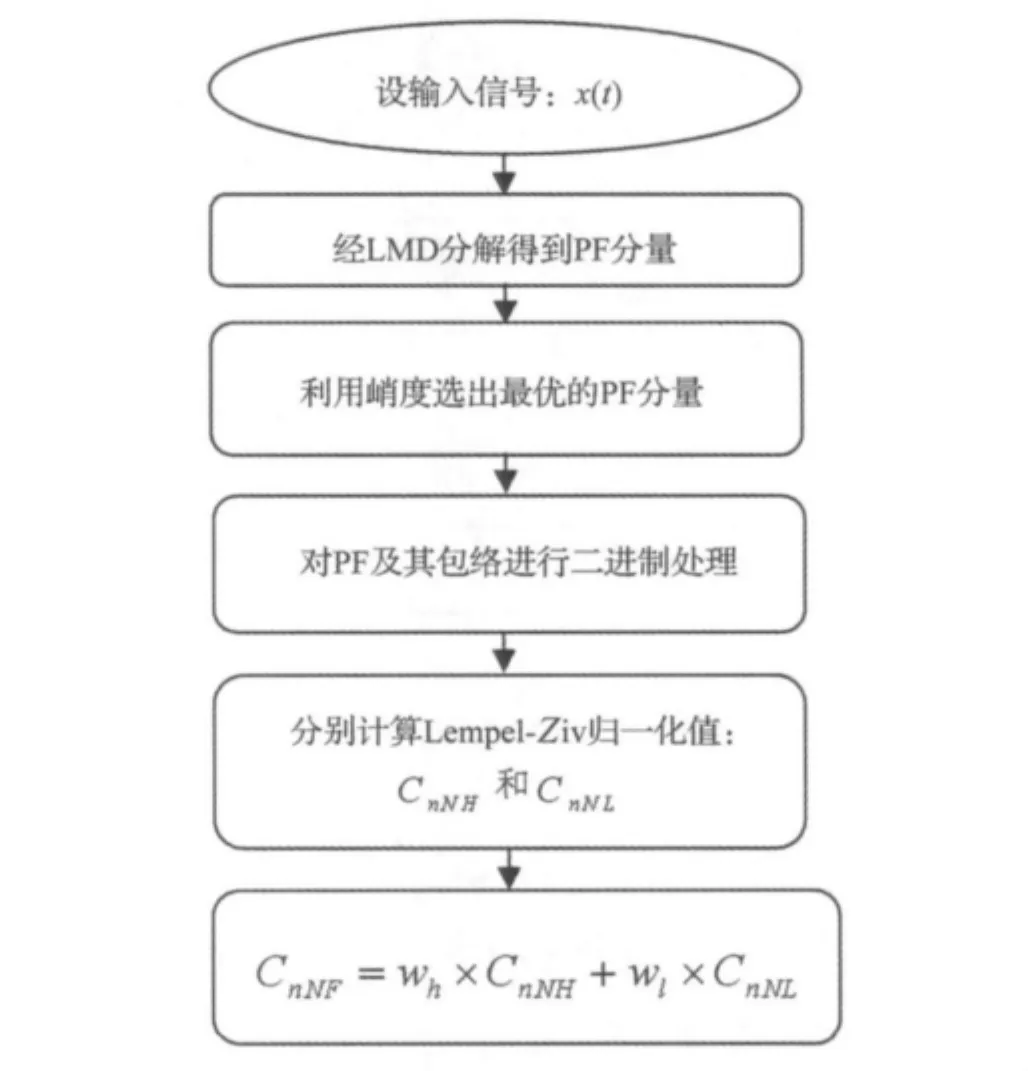
图2 基于LMD和Lempel－Ziv指标的故障诊断步骤图Fig.2 Steps figure of the fault diagnosis based on LMD and Lempel－Ziv index

4 故障诊断实例

实验中轴承型号为308，查机械手册可知：滚动体个数n=8;滚动体直径d=14.288 mm;滚动体节径D=65 mm;接触角α=0。实验数据通过加速度传感器采集，参数为：采样频率20 kHz，采样点数为16 384，滤波频率为10 kHz。分别在转速为500 r/min、800 r/min和1 200 r/min情况下，提取10组信号来进行故障类型的实验，步骤如下：

(1)首先，取相同条件下的实际信号各10个(同一转速)其中包括：正常轴承数据10个、内圈故障轴承数据10个以及外圈故障轴承数据10个。对各个信号进行LMD分解。由于篇幅有限，仅展示一个500r/min内圈损伤的LMD分解得到的PF分量结果，如图3所示。

(2)再次，在每个信号的LMD分解结果中取前8个分量求取Lempel－Ziv指标值。在不同转速下的结果如表1所示(由于篇幅所限表中每种状态只罗列了两个信号的结果)。

由表1可看出，经过LMD分解后求取的各个PF分量的Lempel－Ziv指标值，在不同转速下具有相同的规律性。不管在哪种转速下，外圈故障轴承数据的第一个IMF分量Lempel－Ziv的指标值最大，其次是正常轴承数据的第一个IMF分量Lempel－Ziv的指标值，内圈故障轴承数据的第一个IMF分量的Lempel－Ziv指标值最小。

不经过LMD分解直接求取在800 r/min转速下轴承内外圈损伤振动信号的Lempel－Ziv指标值如表2所示。

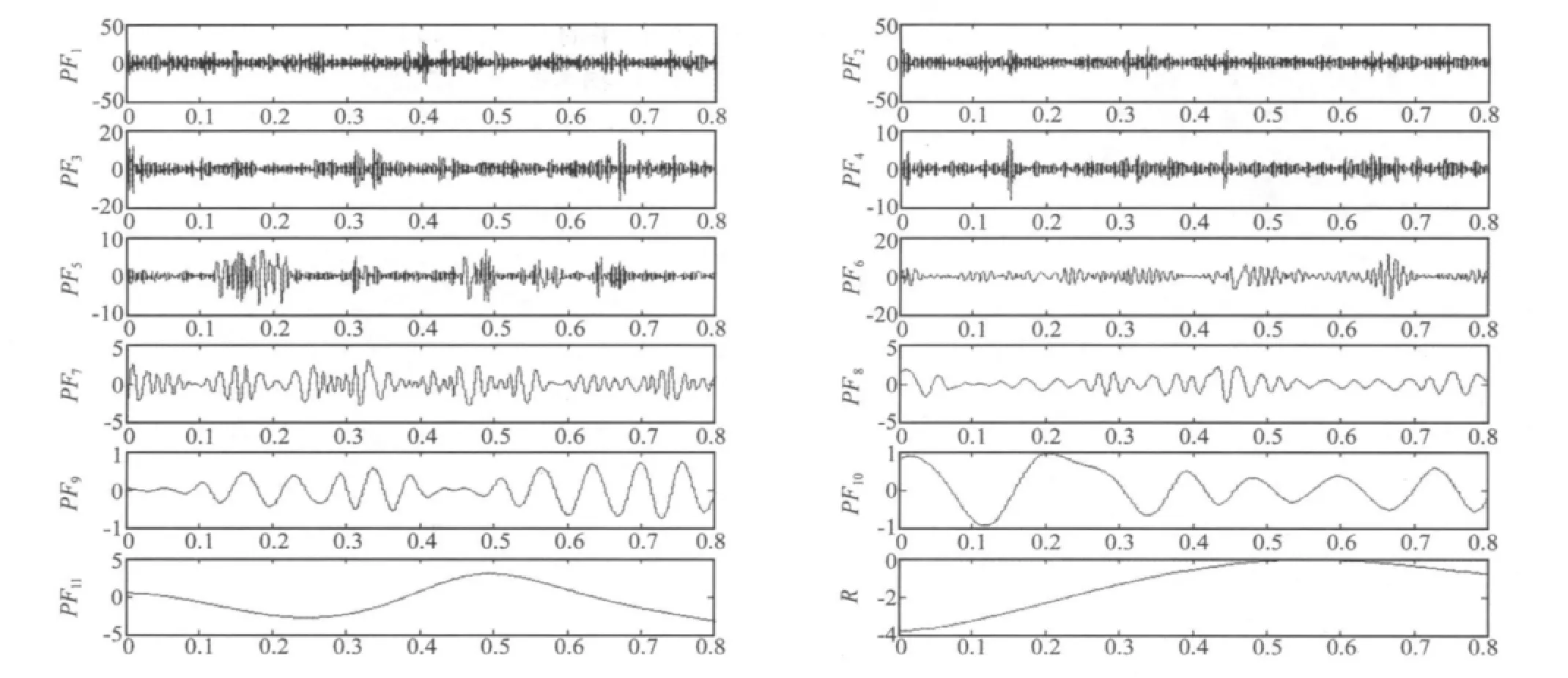
图3 内圈损伤轴承振动信号LMD分解的结果Fig.3 LMD decomposition results of bearing vibration signal with outer race defect

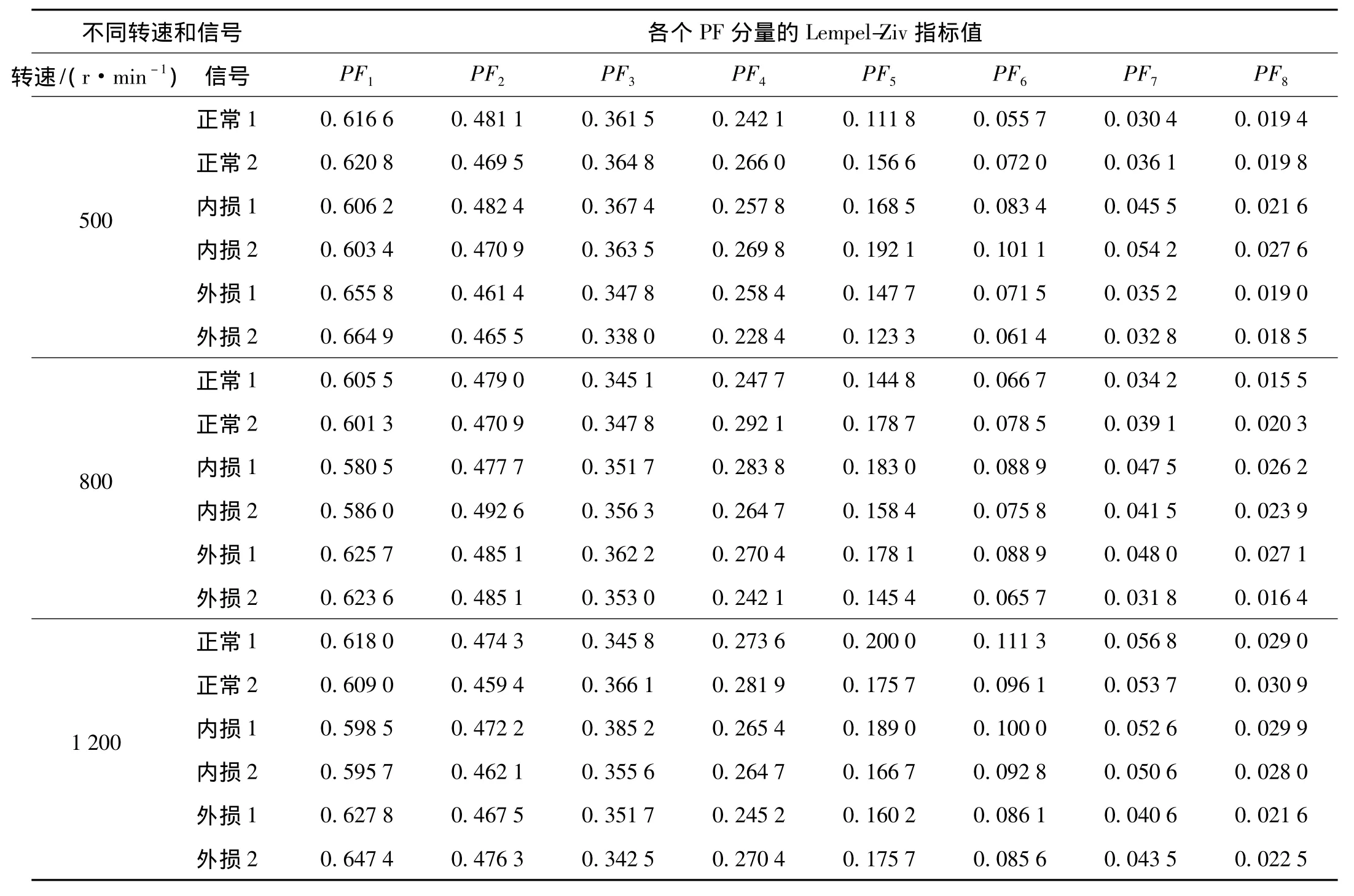
表1 不同转速下轴承振动信号的Lempel-Ziv指标值Tab.1 Lempel-Ziv index of different speed vibration bearing signals

表2中的Lempel－Ziv指标值无规律可言，通过对比表1和表2的结果，可得结论，通过LMD分解求取各个PF分量的Lempel－Ziv指标值可以根据第一个PF分量的Lempel－Ziv指标值判断轴承故障类型。

(3)利用峭度值找到最优PF分量，并求取其综合Lempel－Ziv指标值。由图3中各个PF分量的幅值大小可见IMF1～IMF6幅值都较大，是信号的主要成分，分别计算其峭度值：IMF1的峭度k1=4.276 4，IMF2的峭度k2=4.474 8，IMF3的峭度k3=7.433 2，IMF4的峭度k4=12.231 5，IMF5的峭度 k5=14.503 6，IMF6的峭度k6=5.897 4，因此IMF5为最优信号分量。对IMF5求均值，所有幅值小于等于均值的时刻用0代替，否则用1代替，得到一个二进制序列，按第2.2节中的算法求得CNH=330，再得到归一化的 Lempel－Ziv指标：CnNH=0.168 5;对IMF5求包络，同样二进制化，求得CNL=126，CnNL=0.053 7。根据式(25)可得 Lempel－Ziv 综合指标CnNF=0.091 9。

(4)判断故障损伤程度。表3为不同程度的内圈损伤轴承信号Lempel－Ziv综合指标值对比，可见随着损伤面积的扩大，Lempel－Ziv指标值递减。

外圈故障情况计算方法与内圈相似，只要将权值系数换一下再求取综合指标即可。表4为不同故障程度的外圈损伤轴承Lempel－Ziv综合指标值对比，Lempel－Ziv指标值随故障恶化而递增。在不同转速下进行了验证，得到了与上相同的结论。

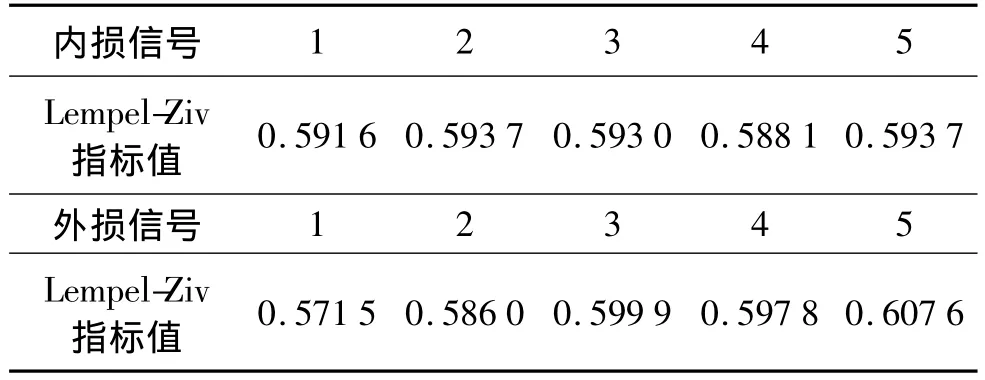
表2 800 r/min转速下轴承振动信号的Lempel-Ziv指标值Tab.2 Lempel-Ziv index of 800 r/min speed vibration bearing signals

表3 内圈损伤轴承Lempel-Ziv指标比较Tab.3 Lempel-Ziv index of 500 r/min speed vibration bearing signals with inner race defect

表4 外圈损伤轴承Lempel-Ziv指标比较Tab.4 Lempel-Ziv index of 500r/min speed vibration bearing signals with outer race defect

5 结论

本文针对不同转速下，不同损伤程度的滚动轴承内、外圈故障，提出一种基于局域均值分解LMD和Lempel－Ziv指标的滚动轴承损伤程度识别方法。通过对实验结果的分析，可得如下结论：

(1)轴承原始振动信号经过LMD分解后，在求其Lempel－Ziv指标，可以通过此指标综合值来判断故障类型。

(2)可以结合峭度条件找出蕴含故障信息的最优PF分量，计算此PF函数和其包络的Lempel－Ziv的归一化值，再加权求和得到最终的Lempel－Ziv综合指标，此指标值可表征不同故障的损伤程度。

(3)内圈损伤轴承信号Lempel－Ziv综合指标值随着损伤面积的扩大指标值递减;外圈损伤轴承Lempel－Ziv综合指标值随故障恶化而递增。

［1］毕 果，陈 进，李富才，等.谱相关密度分析在轴承点蚀故障诊断中的研究［J］.振动工程学报，2006，19(3)：388－393.

［2］段晨东，何正嘉.一种基于提升小波的故障特征提取方法及其应用［J］.振动与冲击，2007，26(2)：10－13.

［3］康海英，祁彦洁，王 虹，等.利用倒阶次谱和经验模态分解的轴承故障诊断［J］.振动、测试与诊断，2009，29(1)：275－277.

［4］ Li C J，Wu S M.On－line detection of localized defects in bearings by pattern recognition analysis［J］.ASME Journal of Engineering for Industries，1989，111：331－336.

［5］Peng Z，Chu F，He Y.Vibration signal analysis and feature extraction based on re－assigned wavelet scalogram ［J］.Journal of Sound and Vibration，2002，253(5)：1087－1100.

［6］窦东阳，赵英凯.基于EMD和Lempel－Ziv指标的滚动轴承损伤程度识别研究［J］.振动与冲击，2010，29(3)：5－8.

［7］Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2(5)：443－454.

［8］程军圣，杨 宇，于德介.局部均值分解方法及其在齿轮故障诊断中的应用［J］，振动工程学报，2009，22(1)：76－84.

［9］ Lei Y G，He Z J，Zi Y Y，et al.A new approach to intelligent fault diagnosis of rotating machinery［J］.Expert Systems with Applications，2008，35(4)：1593－1600.

［10］ Lempel A，Ziv J.On the comp lexity of finite sequences［J］.IEEE Transactions on Information Theory，1976，22(1)：75－81.

［11］Hoonbin H，Liang M.Fault severity assessment for rolling element bearingsusing the Lempel－Ziv complexity and continuous wavelet transform ［J］.Journal of Sound and Vibration，2009，320：452 －468.

Fault severity assessment for rolling element bearings based on LMD and Lempel-Ziv index

ZHANG Chao1，2，CHEN Jian－jun2
(1.School of Information Engineering University of Science and Technology of the Inner Mongol，Baotou 014010，China;2.School of Electronic－Mechanical Engineering Xidian University，Xi'an 710071，China)

For different rotation speeds and different inner or outer race defects severity，a fault severity assessment scheme based on local mean decomposition(LMD)and Lempel－Ziv index was put forward.In LMD method the bearing vibration signal was decomposed into several product functions(PF)with instantaneous frequency having definite physical meaning.The optimal PF component can be found according to kurtosis conditions.On the basis of the best PF，the normalized Lempel－Ziv values for the PF envelope were calculated.Then the values multiplied by given weights were summed up to form a final measure named the integrated Lempel－Ziv index.Different intervals of the index value correspond to different fault severity.At the same time，for making conclusions more universal，the bearing fault Lempel－Ziv index distribution rule of the inner and outer defects at different rotating speed was studied.The experiment results show that the algorithm can be effectively applied in rolling bearing fault diagnosis.

local mean decomposition;Lempel－Ziv index;defect severity;product function;fault diagnosis

TG17

A

内蒙古自治区高等学校科学研究项目(NJZY11148)资助

2011－07－07 修改稿收到日期：2011－09－05

张 超 男，博士，讲师，1978年生

陈建军 男，教授，博士生导师，1951年生