非线性热对流斑图实验
周路群,冉书能,贾春燕
(北京大学 物理学院,北京100871)
1 引 言
以普里高津为代表的布鲁塞尔学派的学者们从近平衡态热力学规律到远离平衡态的热力学系统研究的过程中经历过不小的挫折,然而他们最终提出的耗散结构理论为物理非线性科学带来了几十年的繁荣发展,成为现代物理前沿研究中的一支奇葩.更为引人注目的是耗散结构理论体系中的诸多重要概念现如今已广泛地深入到大众生活中,这是因为耗散结构理论不仅能解释许多物理、化学、生物等自然科学问题,近年来还被引入哲学、社会学、经济学等诸多领域,使之成为当代少数几个能横跨自然与人文社会科学的重要科学理论之一.普里高津于1977年因此获得了诺贝尔化学奖[1].
早在1900年贝纳德就观察到由于对流现象流体形成的花样(斑图),后来瑞利对该系统做了理论分析,故该系统被称为瑞利-贝纳德热对流系统.物理学家们对该系统又做了更为详尽的研究,以平衡态、近平衡态系统到远离平衡态的开放系统这些基本概念为出发点,讨论不稳定性、涨落的作用,提出了从无序到有序的临界转变过程,也即耗散结构(斑图)的发生发展演化过程.这个系统直到现在也仍然吸引科学家们的关注[2].
笔者基于对斑图动力学的研究,参考了文献[3]中的做法,搭建了一套用阴影法观察非线性瑞利-贝纳德热对流斑图发生发展的演化过程的教学装置,并于2010年秋季学期正式纳入到近代物理实验课程的教学体系当中.此装置的引入旨在让高年级本科生通过对经典系统的实验观察体会和理解耗散结构理论,以及相关的基本概念,诸如平衡态、近平衡态、远离平衡态的非线性系统,以及不稳定性、涨落、从无序到有序的转变等.在教学实验中,采用了阴影法[4]对实验现象即斑图进行可视化,并用CCD进行采集和传输数据至计算机进行保存,以便后续分析.因此,该教学实验不仅综合了力学(流体力学)、热学、电学、光学等诸多物理基础领域内的基本知识,而且也使用了现代化的图像采集和计算机技术,综合性很强.
2 实验装置
图1是非线性对流斑图实验装置示意图,研究的对象是由去离子水组成的1层薄对流水层,对流水层的上方是降温水层,2个水层的接触面是蓝宝石片,在透明介质中它具有相对较高的热导率,为46 W/(m·K).降温水层其他部分是有机玻璃,选用透明介质是为了观察对流水层内的斑图,降温水层通过泵将水泵入制冷机,然后流过蓝宝石片带走热量,从而尽可能稳定对流水层的上表面温度.蓝宝石片一侧放置了Pt100,用于测量对流水层的上表面温度,由温控仪A显示温度.热对流水层的下表面是纯紫铜盘的镀金平面,紫铜下面放置硅胶加热片,通电后对紫铜进行加热,紫铜的镀金平面作为反射镜.紫铜具有高的热传导率[为387 W/(m·K)],加热后可保证镀金平面的温度均匀性.下表面温度的测量是用另一个置于紫铜盘和硅胶加热片之间的Pt100,由温控仪B显示温度.热对流水层的上下2个表面温度差的控制和改变是利用通过硅胶加热片的电流来决定的.固定电流,加热片放热的功率一定,在从下而上的热传递过程中整个系统逐渐达到稳定的温度分布,最终在热对流水层的上下2个表面形成稳定的温度差.改变电流,加热片放热功率改变,通过热传递的暂态过程最终形成的稳定的温度差也就会不同.即电流大小的改变决定了对流水层上下2个表面温度差的改变,从而改变对流水层内部的流动状态.

图1 非线性对流斑图实验装置示意图
利用阴影法来观察对流水层内的流动结构即斑图.用激光器做光源,经扩束镜扩束,再经凸透镜形成直径为8 cm的准平行光光束,半反半透镜将准平行光投射到降温水层和对流水层,经铜盘镀金表面反射后经对流水层和降温水层出射,出射光的光强分布反映了对流水层的密度分布,降温水层内只要保持水流速度恒定,为层流状态,对平行光光强分布影响不大.如果热对流水层内不出现流动,平行光光强分布在出射后仍为均匀分布,如果对流水层内出现流动后,其密度各处呈不均匀分布,导致光在各处的折射率不同,因此光通过内有流动的对流水层,平行光光强分布不再均匀,而是依赖于对流水层的折射率亦是密度分布了,此即阴影法.接收屏可接收出射后的光,用CCD拍摄图像并存入电脑.
3 实验过程观察及理论分析
以2012年春季学期中1组学生的实验为例,来说明实验的过程和相应的现象.表1列出了放置好2 mm厚对流水层时所选择的参量即电流的大小变化和相应的上下2个表面的温度及温度差,制冷机温度设定为22℃,室温为28℃.

表1 2 mm厚对流水层条件下选定的参量
由表1可知,随着电流的增加,对流水层的上下2个表面的温度也会相应地增加,只是下表面温度增长比上表面温度增长要多,从而使得对流水层的上下2个表面处在不同温度差条件下.图2给出3个典型的稳定温度差情况下CCD所拍摄的图像,可以清楚地显示对流斑图从无到有的产生过程.

图2 不同温度差条件下CCD拍摄的图像
下面将简单介绍对流斑图产生的相关理论分析[5-6].图3即为本实验的对流系统剖面示意图.上下两边界为水平,温度分别维持为Tu和Tu+ΔT(ΔT>0).
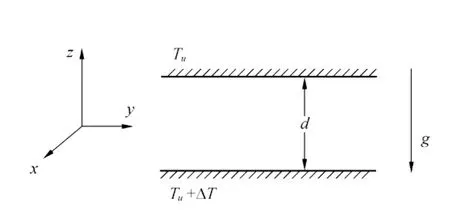
图3 上下温度不同的两无限大平板间的热对流系统剖面示意图
此热对流系统满足鲍兴尼斯克(Boussinesq)条件,相应的热对流基本方程组为:

其中第一个方程由流体力学中纳维-斯托克斯(Navier-Stokes)方程导出,g 是重力加速度,α 是流体热膨胀系数,¯ρ是流体的平均密度.γ=γ′/¯ρ为流体的黏度,这4个物理量加上第3个方程中的热导率κ=κ′/(¯ρcp)为常量.第2个方程为流体连续性方程,第3个方程由热传导方程导出.这个方程组可变物理量为V是流体内速度场,p是压强,T是温度场.由这个方程组可知,加热作用κ▽2T产生了流体中温度变化场T,通过浮力gαT^z可产生和影响对流运动V,而流动后又可通过传输热量V·▽T改变原先的温度分布.结合边界条件,
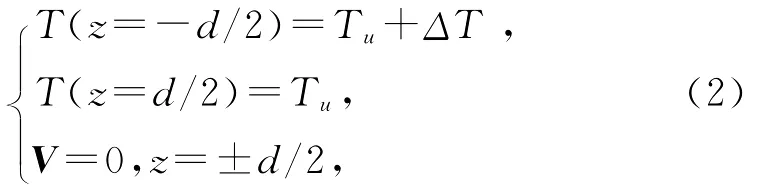
方程组有定常解

而且p0(z)和T0(z)满足:
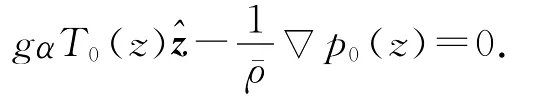
对此定态解我们需要了解其稳定性情况,常用的办法就是线性稳定性分析,即通过对定态解加微扰,讨论微扰的线性发展.假设存在微扰T=T0(z)+θ,p=p0(z)+p′,V=u,代入方程组(1)得到关于微扰满足的方程组,并进行无量纲化后得到无量纲方程组

其中ω≡uz是微扰速度u在z方向的分量,

是瑞利数.
线性稳定性分析方法则是将微扰方程中所有变量视作微扰小量,因此可忽略非线性项,然后假设初始微扰为

方程组(4)是参量方程,其可变参量为瑞利数R,为温度差的函数,通过线性稳定性分析方法可求出定态解(即均匀态)从稳定到不稳定的临界参量,详细推导过程参见文献[7-8].数值计算的结果显示有如下临界参量:

也就是说,当对流水层的上下温差使得瑞利数R<Rc时,系统随机出现的扰动(涨落)会随时间消失,保持定态解稳定;但当R>Rc,满足条件的部分扰动就会逐渐变大,如(6)式中的λc对应的扰动,当它们大到一定程度时,方程中的非线性项就不能忽略,但通常也是只考虑弱非线性作用,常用的方法是多尺度分析,可得扰动振幅所满足的非线性方程,考虑系统对称性后方程的解可用来理解实验结果的斑图分岔行为.由于这部分内容推导过程很复杂,就不详细介绍了[7-8].这里只给出典型的条状斑图的解的形式为:注意到λc的值与π相近,对应波长为1/2,回到有量纲的实际情况有如下结论:条形斑图的半波长与液层的厚度相当.
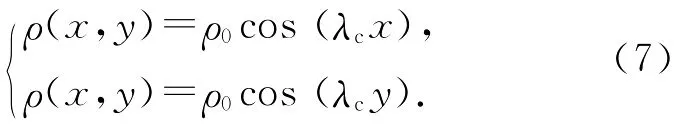
图4可以直观地将理论分析和实验结果结合起来看,图4(a)为温度差较低时满足的瑞利数为R<Rc的情况,此时系统的温度分布满足式(3),为温度梯度在z方向上恒定,且x,y平面处处状态相同,阴影法中均匀光入射,均匀光出射,为一均匀光斑,见图2(a).当温度差升高时使得系统一旦满足的瑞利数为R>Rc的情况时,见图4(b),系统原来定常解失稳,系统自组织起来,形成稳定的对流结构,冷水下降,热水上升,构成对流元胞,即所谓的耗散结构,此时,均匀光入射,由于各处流体密度不同,导致光线偏折,冷水下降处光汇聚,热水上升处光发散,于是出射光的光强重新分布,可以通过所摄的光斑来重构系统内部的对流情况,如图2(b),白线处为冷水下降处,则2条白线之间对应2个对流元胞,为典型的条状斑图,可以用式(7)描述.图2(c)则显示了温度差继续升高,光斑对比度则由于冷热水之间的温差变大而变大.

图4 在不同条件下系统的状态(颜色白表示温度高,颜色灰表示温度低)以及阴影法中均匀入射后出射的情况(箭头表示光的走向)
4 讨 论
在实验教学中,为方便和安全,使用了去离子水作为对流水层,在实验过程中温度不断变化,但可以估算出水的临界温度差,取30℃条件下纯水的参量:κ′=0.62 W/(m·K),γ′=0.8×103Pa·s,α=4.2×10-4K-1,cp=4.2×103J/(kg·K),¯ρ=1.0×103kg/m3,代入式(5)和(6)中,得到临界温度差为

仔细观察前面图像,得到临界温差在6.5~7.8℃之间.之所以不能明确给出实验临界温差,是因为在临界点转变点附近出现的斑图,由于冷热水之间温差较低,导致用阴影法不能获得足够的图像对比度,对判断斑图出现产生困难.另外,一般来说,实验中获得的临界温差要比理论值略微大些,这是因为理论值的获得所针对的系统是在x,y平面内无边界的系统,在实际中做不到,边界是会散热的,所以会出现此结果.
可以估算出斑图的特征尺寸.对流水层直径为64 mm,在图2(b)中直径上可以数出13~14个空间周期的变化.用13个周期来算,可得对流元胞的尺寸大约是2.5 mm,而此系统的厚度为2 mm,可以看出系统斑图的模式选择在很大程度上由厚度决定.另外,可以预计,随着温差的增大,元胞尺寸会增大,在实验中可以明显观察到此变化.
我们认为图2中出现的是条状斑图,这是因为在自组织过程中边界很大程度上会对斑图的形成有影响.理想圆形边界下的条状斑图是完整的同心圆结构.如果在实验前精心清洗过设备各个部件,是能够得到完整的同心圆结构斑图的.这也是斑图的又一个重要特征,对边条件强依赖.只有当直径与厚度比足够大,边界的影响才可以忽略.还有一个问题值得说明,理论方面可以得出另一种对称性高的斑图——六角斑图,但由于斑图的边界依赖性质,它对系统对称要求更高,所以在这套装置上需仔细认真地准备.另一方面,六角斑图出现在临界点附近较小参量范围内,对参量选择要求也较高.
5 结束语
总之,该装置在定量测量上还存在欠缺,这一方面是由于装置的各个部件的光洁度所限,如紫铜盘的镀金表面,限定水层的橡胶圈等,还受限于观察方法,即阴影法.但使用该装置可以很清楚地看到条状斑图从无到有的产生过程,对本科生而言,接触和理解相关的理论尤其是非线性动力学方面及耗散结构理论是相当直观和有帮助的.
致谢:感谢郭葳和朱威頔2位同学提供了实验结果.
[1] 普里戈金.从存在到演化[M].曾庆红,严士健,马本堃,等译.北京:北京大学出版社,2007.
[2] Ahlers G,Grossmann S,Lohse D.Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J].Rev.Mod.Phys.,2009,81:503.
[3] Ciliberto S,Pampaloni E,Pérez-García C.Compitition between different sysmmetries in convective patterns[J].Phys.Rev.Lett.,1988,61(10):1198.
[4] 梅尔兹科奇.流动显示[M].黄素逸,王志国,张浩然,译.北京:科学出版社,1991.
[5] 余志豪,王彦昌.流体力学[M].北京:气象出版社,1982.
[6] Cross M C,Hohenberg P C.Pattern formation outside of equilibrium [J].Rev.Mod.Phys.,1993,65:851.
[7] Chandrasekhar S.Hydrodynamic and hydromagnetic stability[M].Oxford:Clarendon Press,1961.
[8] Busse F H.Non-linear properties of thermal convection[J].Rep.Prog.Phys.,1978,41:1929.

