离轴反射式航天CCD相机镜头焦距的测量方法

曹智睿，吴一丁，吴国栋

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.长春工程技术学院，吉林长春130117）

离轴反射式航天CCD相机镜头焦距的测量方法

曹智睿1，吴一丁2，吴国栋1

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.长春工程技术学院，吉林长春130117）

为了实现离轴反射式航天CCD相机镜头焦距的精密测量，同时降低传统测量方法对大口径长焦距准直管和大型精密旋转平台等昂贵测量装置的依赖，研究了离轴反射式航天CCD相机镜头焦距的测量方法.改进了基于精密测角原理的焦距测量方法，测量装置主要由电子经纬仪和测量显微镜组成；分析比较了该测量方法与传统测量方法的优缺点；建立了该方法求解离轴反射式相机镜头焦距的数学模型和误差分析模型.实际测量结果表明：该方法所使用的测量装置简单易得，节约了测量成本；测量精度达到10－2mm量级，可以满足非测绘用途的离轴反射式航天CCD相机镜头焦距的测量精度要求.

离轴反射式航天CCD相机；焦距；精密测角

1 引 言

随着我国航天事业的飞速发展，国家对航天CCD相机的需求越来越大.离轴反射式光学系统具有分辨率高、体积小、无色差和平像场等优势，已经成为航天CCD相机镜头常采用的该种光学结构，而对其焦距进行精密测量则是质量控制必不可少的重要项目.传统方法对离轴反射式航天CCD相机镜头焦距的测量需要用到准直管和精密旋转平台等测量装置，但是由于航天CCD相机的焦距、口径和体积越做越大，这就要求所使用的准直管的焦距和口径相应地增大，要求所使用的精密旋转平台的直径相应地增大，而这些大型测量装置的研制经费需要几百万元甚至上千万元，且数量有限，不能满足多个航天相机镜头同时测量的需求.因此，采用怎样的测量方法和测量装置；既能满足焦距的测量精度要求，同时又能降低测量过程中对大口径长焦距准直管和大型精密旋转平台等昂贵测量装置的依赖，是光学测量人员普遍关注的问题.

本文根据精密测角原理测量离轴反射式航天CCD相机镜头的焦距，测量装置简单，主要由电子经纬仪和测量显微镜组成，测量精度可以达到10－2mm量级.

2 测量原理

常见的光学系统焦距测量方法为放大率法或精密测角法［4－6］.放大率法测量焦距的原理是基于光学系统的像高与物高的比值等于光学系统的焦距与测量所使用准直管的焦距的比值，其数学模型为

其中：f′为被测光学系统的焦距，fc′为测量所用准直管的焦距，y′为像高，y为物高.由于光学系统存在畸变，按照式（1）测量光学系统不同视场的焦距的测量值各不相同，若畸变较大，其焦距测量值的差别也很大.因此，通常都不采用该方法测量航天相机镜头的焦距.通常基于精密测角原理，在相机镜头的畸变测量同时测量航天相机镜头的焦距.我们将能使被测相机镜头各视场畸变平方和取最小值f′作为被测相机镜头的焦距.

由于离轴反射式航天CCD相机镜头的视轴与光轴分离，其焦距测量的数学模型与同轴光学系统略有不同.基于精密测角原理对离轴反射式航天CCD相机镜头焦距进行测量的模型如图1所示，其中：O′是网格板的中心，同时也是像面主点，O是相机镜头的光轴与像面的交点，H′O′是视轴，H′O光轴，α是视轴与光轴的夹角，A是网格板上一点，O′A＝yi，是离轴视场的像高，ωi是与yi相对应的离轴视场角.Vω为离轴视场角ωi处的绝对畸变，f′为视轴主距，则

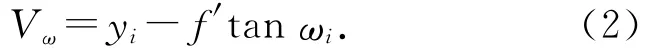
把能使各不同视场角ωi处绝对畸变Vω的平方和取最小值的f′作为视轴主距，即令

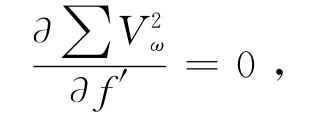
则有：

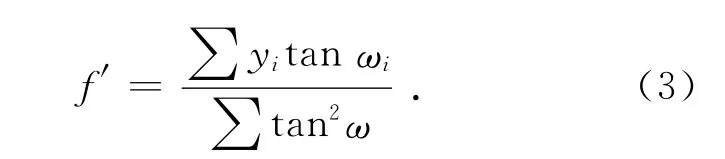
离轴反射式相机镜头的焦距f可按式（4）计算：

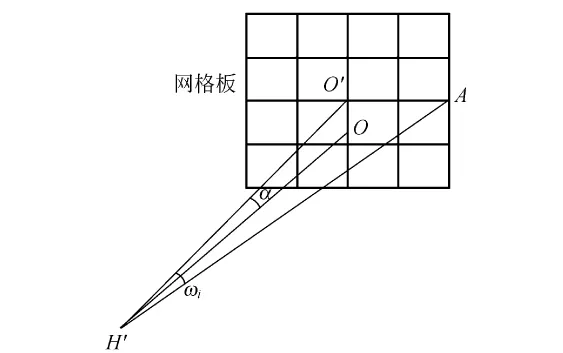
图1 焦距测量示意图

3 测量方法及装置

3.1 传统测量方法及装置

传统精密测角法的测量光路如图2所示.

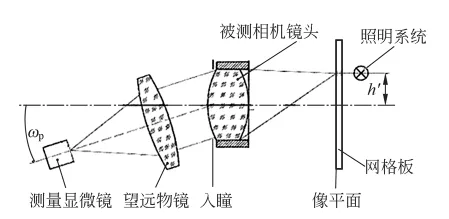
图2 传统精密测角法的测量光路

测量装置主要由准直管、精密旋转平台、测量显微镜和精密网格板组成.对测量装置的要求包括：准直管的焦距应为被测相机镜头焦距的2～5倍；精密旋转平台的直径应大于被测相机镜头的尺寸，保证被测相机镜头安全平稳.

测量的具体步骤如下：

1）精确标定出被测相机镜头的像平面，保证测量中的像平面与实际使用的像平面一致.

2）将被测相机镜头固定在精密旋转平台上，调整被测相机镜头的光轴与准直管的光轴同轴.

3）在被测相机镜头像平面安装网格板，保证网格板刻划面与像平面重合.在准直管的像面处通过测量显微镜观察网格板目标的像，调整网格板在全视场内成像清晰，无倾斜和主点偏移.

4）转动被测相机镜头，通过测量显微镜使其十字丝的像与网格板上各已知点对准，记录精密旋转平台的方位角读数值（即物方视场角）和网格板上对应的像高，通过式（3）和式（4）可以求解被测相机镜头的焦距.

3.2 改进的测量方法及装置

改进后的精密测角法的测量装置如图3所示.测量装置主要由电子经纬仪、测量显微镜、精密网格板和稳定的气浮平台组成.

图3 改进后的焦距的测量装置

测量的具体步骤如下：

1）精确标定出被测相机镜头的像平面，保证测量中的像平面与实际使用的像平面一致.

2）将被测相机镜头放置在稳定的气浮平台上，在被测相机镜头的物方放置电子经纬仪，像方放置测量显微镜，搭建如图2所示测量光路.

3）调整电子经纬仪的位置使其望远镜的出瞳中心与被测相机镜头的入瞳中心尽量重合，并以相机镜头的指向立方镜为基准，通过调整相机的支撑结构使相机镜头的视轴与电子经纬仪望远镜的光轴同轴.

4）在被测相机镜头像平面安装网格板，保证网格板刻划面与像平面重合.将电子经纬仪调焦至无穷远，通过测量显微镜观察网格板刻线和电子经纬仪的十字丝在被测相机镜头焦面上成的像，调整网格板刻线无倾斜，网格板中心与被测相机镜头像面主点无偏移.

5）转动电子经纬仪，并通过测量显微镜使电子经纬仪的十字丝的像与网格板上各已知点对准，记录下电子经纬仪的方位角读数值（即物方视场角）和网格板上对应的像高，通过式（3）和式（4）可以求解被测相机镜头的焦距.

3.3 理论分析与比较

上述2种测量方法均是基于精密测角原理，但是所使用的测量装置不同，测量过程中观察面的选取也不同.本文介绍一台特殊设计的离轴三反式航天CCD相机镜头，其焦距设计值为6m，离轴角为0.3°，相机镜头长约1.8m，宽约1m.通过理论分析比较2种测量方法在该相机镜头焦距测量过程中优缺点.

若采用传统精密测角法，测量装置选取焦距18m（或焦距更长）的准直管、直径2m，测角精度为0.5″的大型精密旋转平台和放大倍率为40倍的测量显微镜，测量显微镜的十字丝线宽为0.02mm，网格板刻线宽为0.02mm.网格板刻线在准直管焦面处的像宽理论上等于0.06mm，对应的角度为0.7″.测量时用十字丝压线网格板目标的像，人眼的压线对准精度为60″，由应用光学的知识可求得放大倍率为40倍的测量显微镜采用压线对准方式对准时物方的对准误差为Δy：

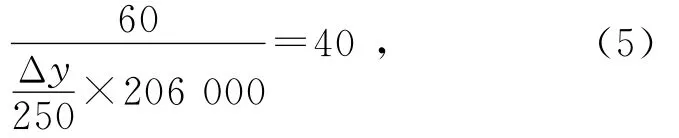
Δy＝0.002mm，相对对准误差为0.033，对应的角度为0.023″.

若采用改进后的精密测角法，测量装置选取焦距为150mm，测角精度为0.5″的小型电子经纬仪和放大倍率为40倍的测量显微镜，电子经纬仪的十字丝线宽为0.02mm，网格板刻线宽为0.02mm.电子经纬仪在被测相机镜头像面处的像宽理论等于0.8mm，对应的角度为27.5″.测量时由于十字丝的像宽远大于网格板刻线宽度，对准方式可认为是夹线对准，人眼的夹线对准精度为10″，由应用光学的知识可求得放大倍率为40倍的测量显微镜采用夹线对准方式对准时物方的对准误差为Δy：

Δy＝0.000 3mm，相对对准误差为0.000 4，对应的角度为0.01″.

通过理论分析，2种测量方法的对准精度均远远高于所使用的测角装置的测角精度，其最终的测角精度取决于所选用的精密旋转平台和电子经纬仪的转角测量精度.

由此可见，改进后的精密测角法的优点在于：测角过程中对准精度高；测量装置简单，节约了测量成本.改进后的精密测角法的缺点在于：目前小型电子经纬所能达到的最高转角测量精度低于大型精密旋转平台，在焦距测量精度要求极高的情况下（如用于精密测绘的相机镜头焦距测量），选用转角测量精度更高的大型精密旋转平台可以提高测量精度.

4 误差分析与计算

4.1 测量误差源

采用改进后的测量方法测量离轴相机镜头的焦距主要的误差［7］来源有：测角误差和网格板标定误差.

1）测角误差主要由对准误差和电子经纬仪的转角测量误差构成.由于该方法的对准精度均远远高于电子经纬仪的转角测量精度，其最终的测角误差即为电子经纬仪的转角测量误差.目前，实验室常用的高精度电子经纬仪的转角测量误差可达到0.5″，取δω＝0.5″.

2）网格板经过计量部门的精密标定，其最大标定误差为1μm，取δy＝1μm.

4.2 误差计算

在焦距的测量过程中，所有网格板的标定误差和每次测角的误差都对测量结果产生影响，所以相机镜头焦距的测量误差应按照式（7）计算：

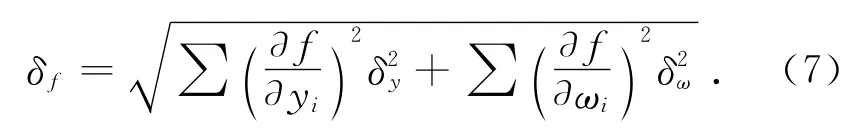
5 实测验证

用改进后的测量方法对本文介绍的离轴三反射相机镜头的焦距进行实际测量.测量所使用的电子经纬仪为莱卡TM5100A型电子经纬仪；测量所使用的测量显微镜物镜为4×，目镜为10×；测量所使用的网格板长度为280mm，网格间距为20mm.测出每个网格对应的物方视场角ωi，共得到15组数据，如表1所示.

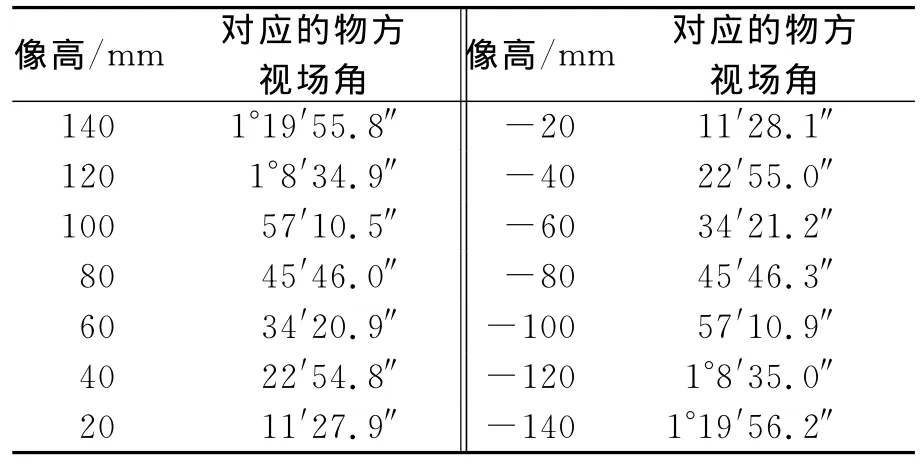
表1 焦距测量的原始数据

根据式（2）和式（3）求解被测相机镜头的焦距为6 013.93mm，满足总体（6 000±15）mm的技术指标要求.根据式（4）得到焦距测量的绝对误差为0.03mm，相对误差为0.000 5%，满足总体提出的测量精度要求.

6 结 论

该改进后的测量方法已经在多个离轴反射式航天CCD相机镜头焦距的测量工作中应用，其测量装置简单，大大降低了测量成本；通过对某离轴反射式航天CCD相机镜头焦距的实际测量，该方法的测量精度达到10－2mm量级，满足了总体提出的焦距测量精度要求，适合非测绘用途的离轴反射式航天CCD相机的焦距测量工作.

［1］ 杨晓飞，张晓辉，韩昌元.Zemax软件在离轴三反射镜系统计算机辅助装调中的应用［J］.光学精密工程，2004，12（3）：120－121.

［2］ 赵文才.改进的离轴三反光学系统设计［J］.光学精密工程，2011，19（12）：2828－2836.

［3］ 薛栋林，郑立功，张峰.基于光学自由曲面的离轴三反光学系统［J］.光学精密工程，2011，19（12）：2813－2820.

［4］ 赵建科，周艳.小视场长焦距镜头畸变高精度测量研究［J］.应用光学，2008，29（3）：381－383.

［5］ 吴国栋.离轴三反时间延迟积分CCD相机内方位元素和畸变的标定［J］.光学精密工程，2012，20（3）：462－467.

［6］ 吴国栋，韩冰，何煦.精密测角法的线阵CCD相机几何参数实验室标定方法［J］.光学精密工程，2007，15（10）：1629－1631.

［7］ 费业泰.误差理论与数据处理［M］.北京：机械工业出版社，2003：67－74.

Measuring focal length of off－axis reflective space CCD camera

CAO Zhi－rui1，WU Yi－ding2，WU Guo－dong1
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Changchun Institute of Engineering Technology，Changchun 130117，China）

A new method was suggested to measure accurately the focal length of off－axis reflective space CCD camera with less dependence on expensive collimator of large aperture and long focal length and large precision rotating platform.The traditional method based on precise angle measurement was improved.The measuring device was composed of electronic theodolite and measuring microscope.The advantages and disadvantages of the new method and the traditional methods were analyzed and compared，and the mathematical models of the camera lens focal length and error analysis were solved.The measurement results showed that the measuring device used in this method was simple，and the measurement accuracy was 10－2mm which satisfied the requirement of off－axis reflective space CCD camera lens focal length measurement in cases of non－mapping uses.

off－axis reflective space CCD camera；focal length；precise angle focal length measurement

TH703

A

1005－4642（2012）08－0024－04

［责任编辑：郭 伟］

2012－04－10

曹智睿（1983－），男，吉林长春人，中国科学院长春光学精密机械与物理研究所助理研究员，硕士，主要从事光学检测技术的研究.