金属线膨胀系数、德拜温度和杨氏模量之间关联特性

于长丰，蒋学芳，成鹏飞，朱长军

（西安工程大学理学院物理系，陕西西安710048）

金属线膨胀系数、德拜温度和杨氏模量之间关联特性

于长丰，蒋学芳，成鹏飞，朱长军

（西安工程大学理学院物理系，陕西西安710048）

利用解析势能函数研究了FCC，HCP及BCC共19种金属的线膨胀系数、德拜温度和杨氏模量等之间的关联性，给出了金属的德拜温度和杨氏模量的解析计算式，其理论计算值与实验值符合较好.

势能函数；力常数；线膨胀系数；德拜温度；杨氏模量

1 引 言

金属的各种物性参量（如晶格常量、线膨胀系数、德拜温度、杨氏模量、熔点等）之间存在着一定的内在联系，从理论上寻找它们之间的关联规律一直是理论工作者感兴趣的问题，其研究不仅有理论价值而且对材料实验科学和材料工程科学也有一定的指导意义.由于这一工作的重要性，已有不少人开展了这方面的研究工作［1－4］.本工作将文献［5］提出的一种解析势能函数处理成金属原子之间的等效两体势，研究了金属结合能、平衡核间距、德拜温度、线膨胀系数之间的内在联系，并且给出了金属德拜温度和杨氏模量的解析计算关系.

2 金属物性参量之间的关联性及德拜温度和杨氏模量的解析计算

文献［5］给出了用于研究双原子分子光谱的解析势能函数，研究发现该势能函数同样适用于研究金属原子之间的相互作用，进而给出金属的各种物性参量如线膨胀系数、德拜温度、杨氏模量之间的关联特性.

文献［5］给出的解析势能函数为

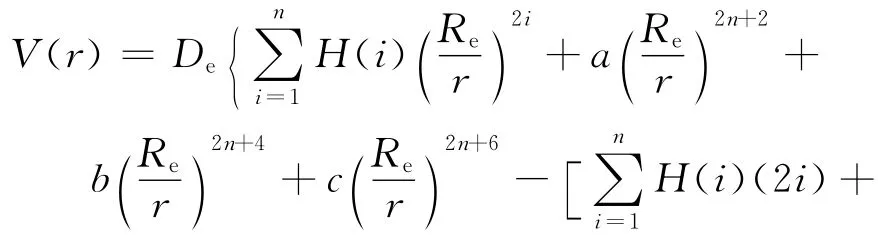
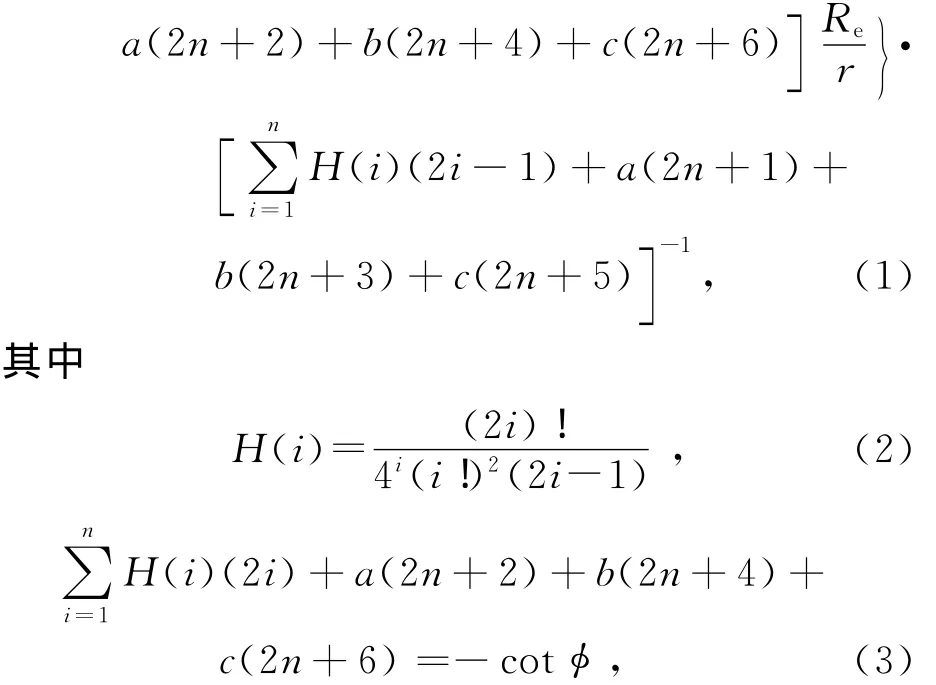
式（1）中a，b，c为待定参量，Re为原子之间的平衡核间距，De为原子的结合能，n取正整数.对于金属可选取n＝3作为两金属原子之间的等效两体势，并对所有金属选取

这样式（1）就化成

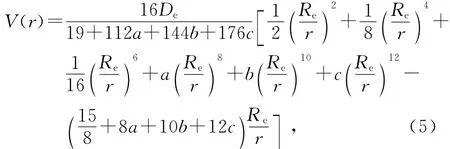
式（5）即为两金属原子之间的等效两体势.另外，在平衡核间距Re处，金属的各阶力常量可以由下式计算：

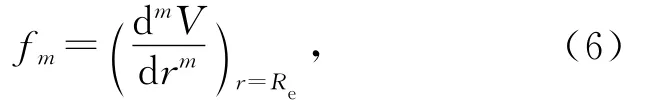
这样由式（5）和式（6）可给出如下方程组

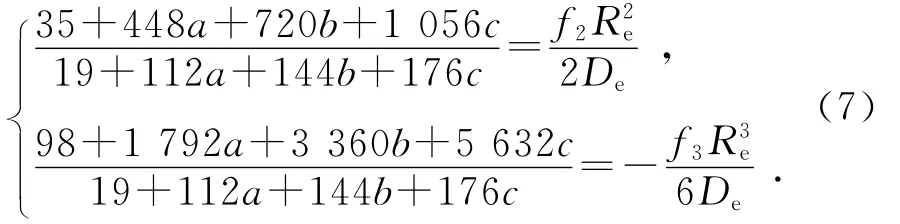
计算表明，对不同类型金属而言，势参量a与b之间存在一定经验关系，即

对于FCC，HCP，BCC金属，ξ分别为1.09，0.95，1.另外，金属二阶力常量f2与金属原子谐振频率ωe还满足如下关系

其中：μ为两金属原子约化质量，c为真空中光速.根据文献［1］，金属的线膨胀系数可定义为

式中k为玻尔兹曼常量.本工作是根据金属的线膨胀系数和结合能并结合势能函数式（5），从理论上计算出金属的德拜温度和杨氏模量.由式（3）、式（4）以及式（7）、式（8）和式（10），可以得到如下方程组：

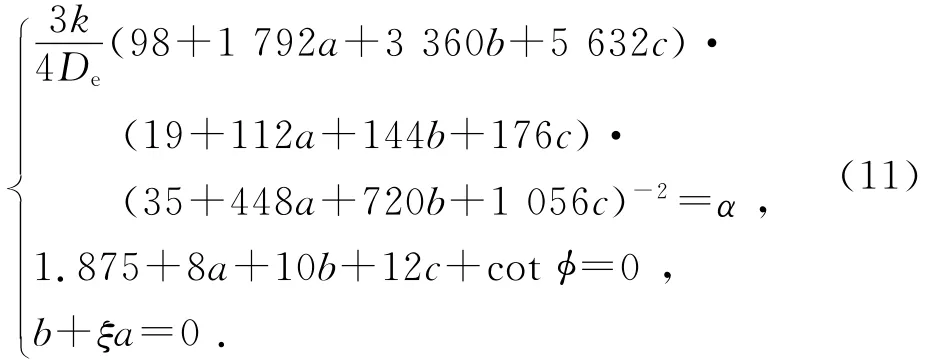
解方程组（11）便可求出势参量a，b，c.注意到式（7）和式（9）及ωD＝2πωec，金属的德拜温度可用下式计算

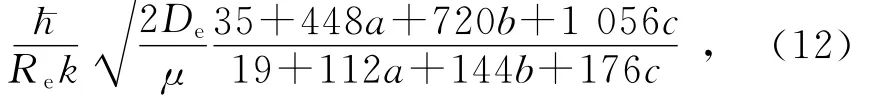
式中：ωD为金属的德拜频率，¯h为普朗克常量.利用文献［1］给出的金属杨氏模量计算式

由式（9）和式（12）可得

式中比例系数ζ与金属类型有关，对FCC，HCP，BCC金属，ζ的取值分别为1／3，0.42和0.38.作为比较，将文献［1－2］给出的金属杨氏模量计算式也引入本文，该计算式为

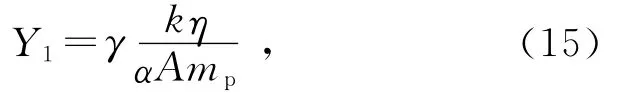
其中：γ＝1.787 283（FCC）或γ＝1.429 826（HCP，BCC），k＝1.380 66×10－23J／K（玻尔兹曼常量），η为金属密度（kg／m3），A为金属原子质量数，mp为质子质量，α为金属的线膨胀系数.

表1是利用式（11）～（15）计算出的3种类型金属（表中Al～Pt，Be～Hf，V～Fe分别为FCC，HCP和BCC金属）的势参量以及德拜温度和杨氏模量［2，6－8］.

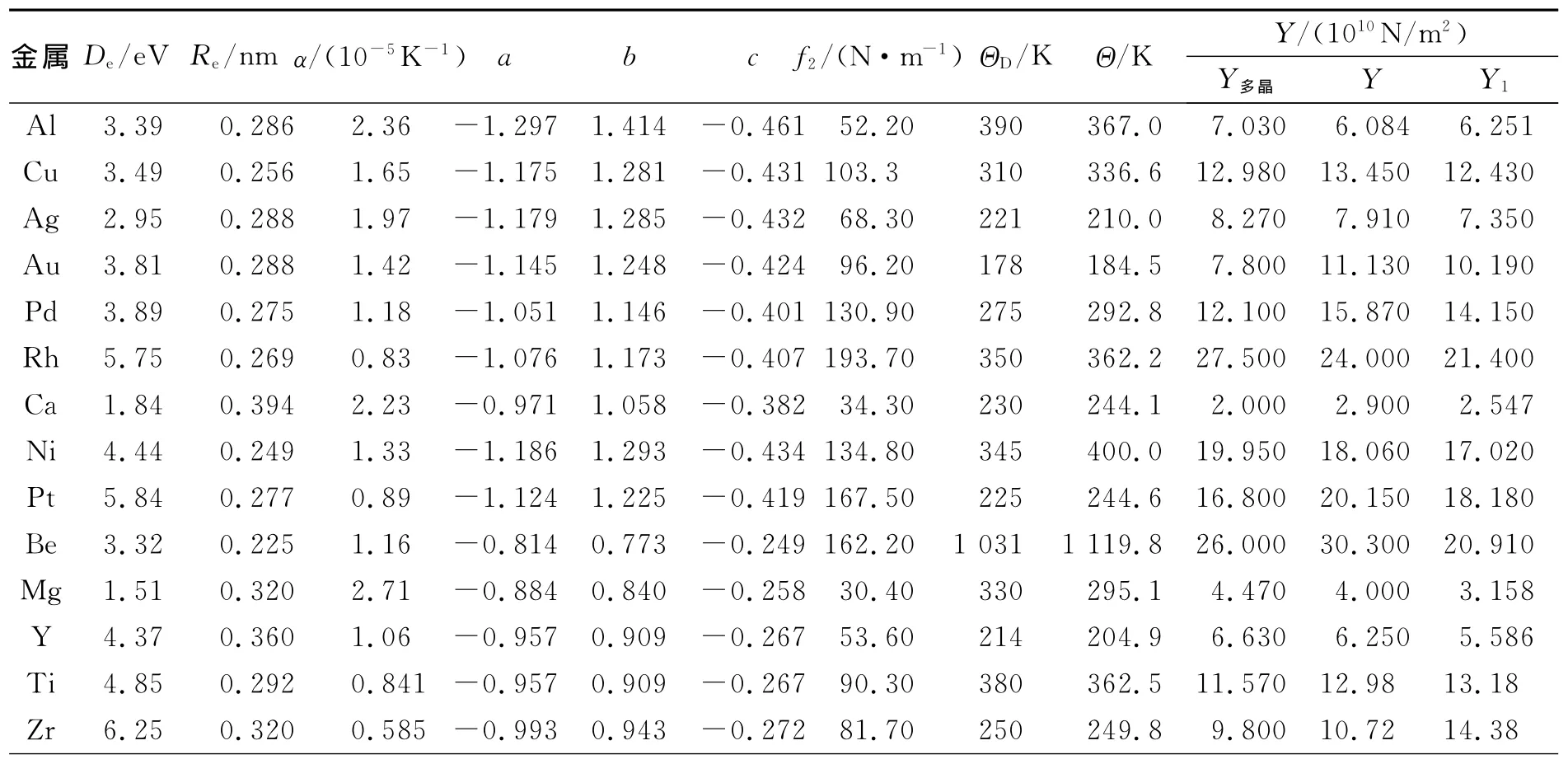
表1 金属的势能参量、力常量、德拜温度和杨氏模量计算值

续表

为了检验式（12）和式（14）及式（15）的计算精度，对表1的19种金属给出相对均方根误差估计，相对均方根误差计算结果如下：

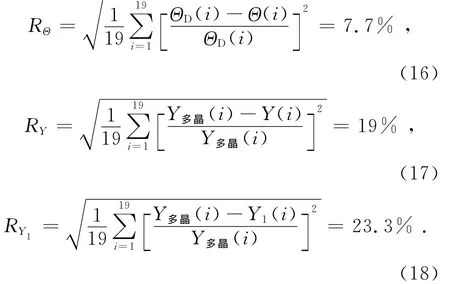
由以上计算结果可以看出，金属德拜温度的相对均方根误差较小，而杨氏模量的相对均方根误差较大.引起杨氏模量的相对均方根误差较大的原因是大部分杨氏模量理论计算值与实际值符合较好，而个别金属（如Au，Ca，Pd等）其理论值与实际值偏差很大.事实上，金属多晶体的杨氏模量是多个晶轴方向上的统计平均值，不同晶轴方向上有不同的杨氏模量值，例如Au在［111］晶轴方向上杨氏模量取得最大值为Y＝11.67× 1010N／m2，而在［100］方向上取得最小值Y＝4.29×1010N／m2［2，9］，表1中Cu，Ag，Au，Ni，Fe等其杨氏模量理论计算值均落在了不同晶轴方向上杨氏模量最大值和最小值之间，即Ymin≤Y≤Ymax

［9］.其余金属尚未见到单晶体杨氏模量实验值.文献［2］和［9］曾给出的一个FCC金属杨氏模量计算式

式中ξ是与金属结构等有关的系数，对于FCC金属，可取值为2.333.

文献［10］曾给出FCC金属Cu的多原子相互作用势函数和势能曲线，其势函数为

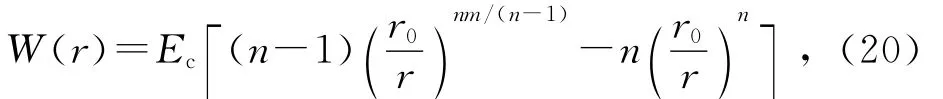
式中：Ec为金属元素的结合能，r0为平衡核间距.文献［10］给定的参量为Ec＝336.6kJ／mol＝3.49eV，n＝1.343，m＝2.507，r0＝0.254 8nm.为了进行比较，图1和图2分别是由势能函数式（5）和式（20）绘制的FCC金属Cu的势能曲线（图1势参量取之于表1中的金属Cu）.

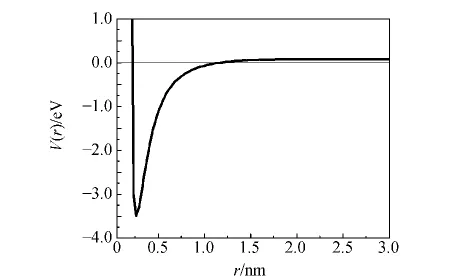
图1 由式（5）绘制的FCC金属Cu势能曲线

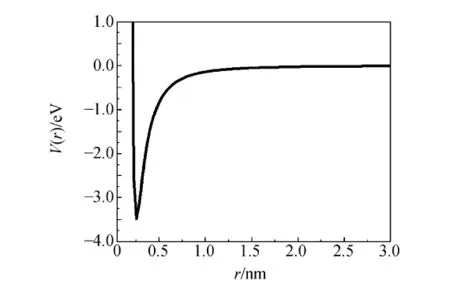
图2 由式（20）绘制的FCC金属Cu势能曲线

3 结 论

用解析势能函数作为两金属原子之间相互作用的等效两体势，用于研究金属的各种物性参量之间的关联规律或进行相关参量计算，取得较好结果.根据表1和式（16）及式（17），德拜温度的理论计算值与实验值比较接近，但杨氏模量的相对均方根误差较大，表1中个别杨氏模量的理论计算值与实验值比较如Au其相对误差达33%.尽管如此，Au杨氏模量的理论计算值与Au单晶体的杨氏模量实验最大值接近（Au单晶体Ymax＝11.67×1010N／m2）［2，9］.其余一些金属杨氏模量的理论计算值也均落在金属单晶体杨氏模量实验最大值和最小值之间或接近其最大值或最小值.

［1］ Yu Changfeng，Yan Kun，Liu Daizhi.A universal analytic potential－energy runction based on a phase factor［J］.Acta Metallurgica Sinca（English Letters），2006，19（6）：455－468.

［2］ 于长丰.相位力学原理［M］.北京：国防工业出版社，2007：26－233.

［3］ 于观夏，林扬帆，苏峻，等.振动法同时测定动态杨氏模量和剪切模量［J］.物理实验，2011，31（3）：1－3.

［4］ 徐嘉彬，袁海甘，吴鸿斌，等.弯曲共振法测量材料的杨氏模量实验改进［J］.物理实验，2011，31（11）：43－46.

［5］ YU Chang－feng，ZHU Chang－jun，ZHANG Chonghui，et al.A novel analytic potential function aapplied to neutral diatomic molecules and charged ions［J］.Natural Science，2010，2（3）：184－189.

［6］ 韦丹.固体物理［M］.北京：清华大学出版社，2004：8.

［7］ 张邦维，胡望宇，舒小林.嵌入原子方法理论及其在材料科学中的应用——原子尺度材料设计理论［M］.长沙：湖南大学出版社，2003：212，222，291－292.

［8］ 连法增.材料物理性能［M］.沈阳：东北大学出版社，2005：251－259.

［9］ 于长丰，杨新铁，阎坤，等.由微观参量表示的金属单晶体杨氏模量的解析计算式［J］.物理实验.2004，24（8）：43－47.

［10］ 陶辉锦，谢佑卿，彭红建，等.fcc－，亚稳hcp－和bcc－Cu的原子状态及物理性质随温度的变化关系［J］.金属学报，2006，42（6）：565－571.

Correlations among linear expansion coefficient，Debye temperature and Young modulus of metals

YU Chang－feng，JIANG Xue－fang，CHENG Peng－fei，ZHU Chang－jun
（Department of Physics，College of Science，Xi’an Polytechnic University，Xi’an 710048，China）

The correlations among linear expansion coefficient，Debye temperature and Young modulus of 19kinds of FCC，HCP and BCC metals were studied by using the potential energy function.Then the analytical formulas for calculating Debye temperature and Young modulus of metals were given.The calculated values were consistent with the experimental data.

potential energy function；force constants；linear expansion coefficient；Debye temperature；Young modulus

TG14

A

1005－4642（2012）08－0037－04

［责任编辑：郭 伟］

2012－01－18；修改日期：2012－03－24

国家自然科学基金资助项目（No.11004156）

于长丰（1962－），男，河北武邑人，西安工程大学理学院物理系副教授，主要从事理论物理及计算物理研究.