多单元永磁同步电机数学模型与转矩波动抑制

邹继斌，赵博，梁维燕，2，徐永向

(1.哈尔滨工业大学 电气工程系，黑龙江 哈尔滨150001;2.哈尔滨电站设备集团公司，黑龙江 哈尔滨150040)

0 引言

大功率低速大扭矩永磁同步电机在国防与国民经济中有越来越广泛的需求，如船舶及战舰推进、轧钢、石油矿山等[1]。然而，随着这种直驱式永磁同步电机的功率逐渐升高，其系统对功率器件的等级要求随之升高，这也限制了大扭矩永磁直驱电机的发展。为解决电机容量与功率器件等级的矛盾关系，大功率永磁电机的设计多采用多单元或者多相化设计，不但可以降低驱动支路的容量，而且还具备一定的容错运行能力。

多单元电机是指电机本体包含多个单元电机，每个单元独立连接一台三相驱动器，各单元电机及驱动器可以同时运行，也可以部分单元运行。永磁多相电机与多单元电机的区别不仅体现在本体设计上，还体现在驱动器拓扑结构和控制策略上[2－3]。多相电机在运行时，控制上较复杂[4－5]。相比较而言，多单元电机控制简单，若某一支路绕组出现开路故障时，可将故障单元电机切除，其余单元电机相电流维持不变，不必调整其幅值相位，容错运行非常方便[6]。各个单元电机虽在电路上并不相连，但是因各单元电机绕组共用一个定子铁心，存在磁路上的耦合关系。当转子磁极为凸极结构时，因绕组空间间距并不相同，将引起绕组间互感不平衡，而在三相对称电流条件下，互感中二次项的不对称将引起定子侧磁阻转矩波动。针对该类转矩波动给出注入3次谐波电流的进行抑制方法[7]。最后，采用数值分析和试验验证的方法对所得的解析公式进行相关印证。

1 多单元电机的电压方程

以一台额定功率2 MW额定转速100 r/min的5单元永磁同步电动机为研究对象，其系统拓扑图如图1所示。

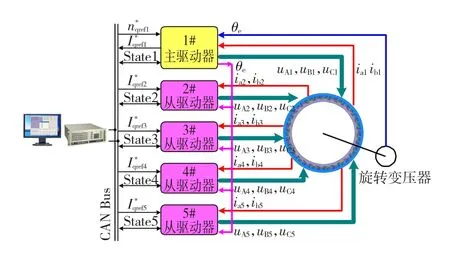
图1 2 MW五单元永磁同步电动机系统Fig.1 2 MW five units PMSM system

因多单元电机单元内部及单元电机间绕组互感不完全相同，所以传统三相电机或多相电机的数学模型无法直接应用于多单元电机分析中，因此有必要建立其相关数学模型。

1.1 多单元电机整机运行时的电压方程

以五单元电机为例，为简化电压表达式，采用分块矩阵的方式进行整机电压方程列写，其方程为

式中:Ui和Ii(i=1，2，3，4，5)表示每个单元的三相电压和电流列矩阵;Ra为每相绕组电阻;If为转子永磁体等效励磁电流;L为每个单元电机内部的三相绕组电感矩阵;Mij(i，j=1，2，3，4，5，i≠j)为各个单元间的互感矩阵;MTij(i，j=1，2，3，4，5，i≠j)为单元间互感矩阵的转置;Msri(i=1，2，3，4，5)是每个单元电机定、转子之间互感矩阵，其表达式完全相同。

每个单元电机的三相电流完全对称，所有单元共同运行时，可等效为三相电机。

1.2 单元电机内部的三相电感矩阵

因为每个独立的单元电机三相绕组仅仅占据定子空间一部分扇区，所以三相绕组在空间上互感磁链不完全相等，这将引起同一单元电机内部三相绕组间互感不完全一致。对多单元电机进行有限元数值分析，可以得到空载时一个单元电机内的三相绕组互感系数，如图2所示。

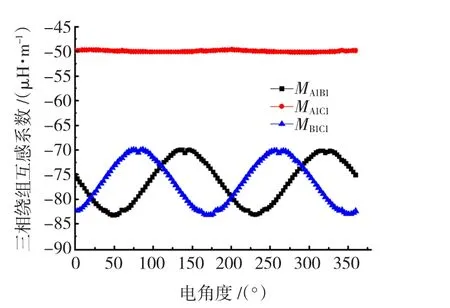
图2 单元电机内部绕组互感系数Fig.2 Coefficient of mutual inductances in one unit motor

计算结果反应出，单元电机内部存在严重的互感不对称现象，由于转子采用了凸极结构，所以电感中含有2次波动项。不同单元电机内部电感矩阵完全一致，在此仅给出1号单元电机的电感矩阵及各元素表达式，即

式中:互感恒定分量与二次波动分量满足不等式MS00＞MS01，MS20＞MS21;互感下角标第一个数字0代表其恒定分量，2代表其二次分量;互感下角标第二个数字表示两相绕组中间间隔绕组的相数，0表示两绕组紧邻，1表示两绕组中间间隔一相绕组，其余与之类似。

1.3 不同单元电机间的互感矩阵

多单元电机这种非对称共磁路的绕组拓扑结构不仅仅引起单元电机内部三相绕组互感不对称，还会引起单元电机间各相绕组互感也不相等。因单元电机圆周循环排布，公式(1)中的各个单元电机间互感矩阵的函数关系式为

在此，仅列写1号与2号单元电机间的互感矩阵，其余各单元电机间互感矩阵可对应依照给出。1号与2号单元电机间互感矩阵为

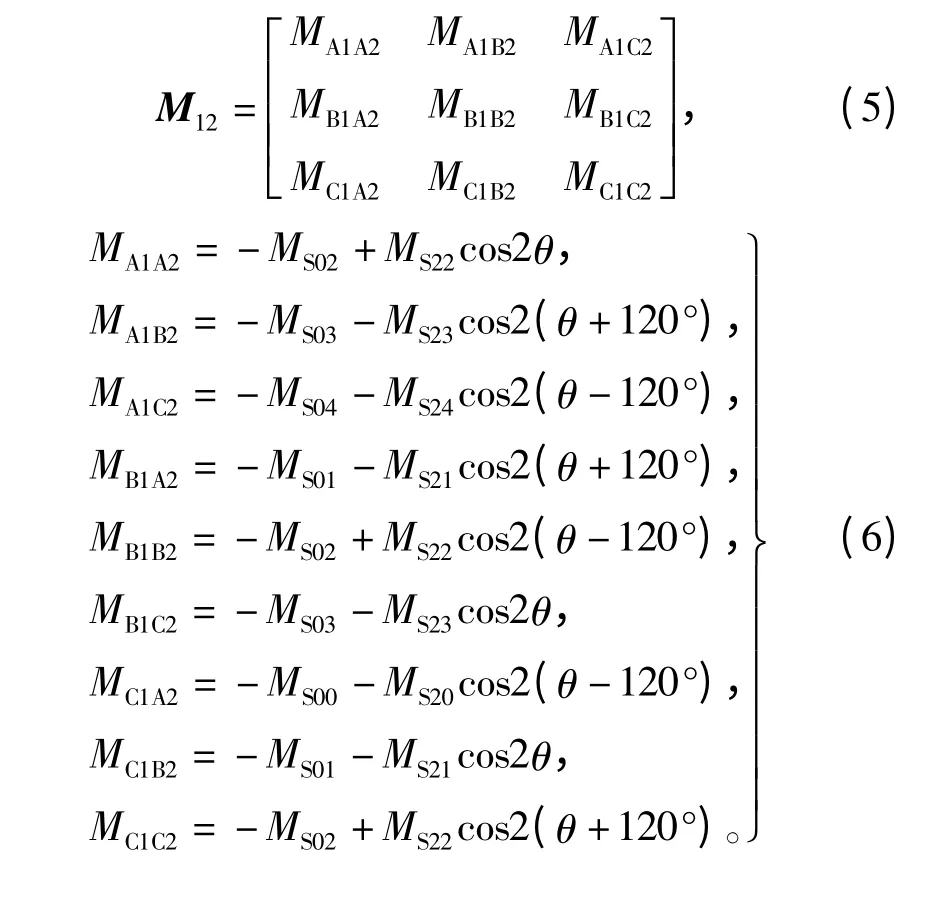
其中，有如不等式(7)所示的关系成立，即

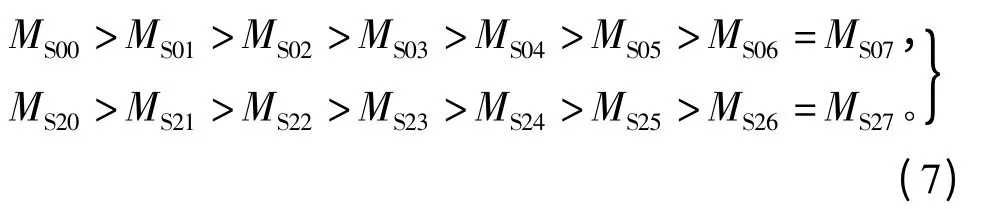
1.4 部分单元电机运行时的电压方程

多单元电机某一相绕组发生开路故障时，可以直接将故障单元整体切除，而剩余的工作绕组仍可继续维持电机的正常运行，且各单元绕组中的电流幅值和相位无需再次进行调整。

在此，假设仅1号、2号和3号相邻三单元共同运行，则部分单元运行时的电压方程可以列写为

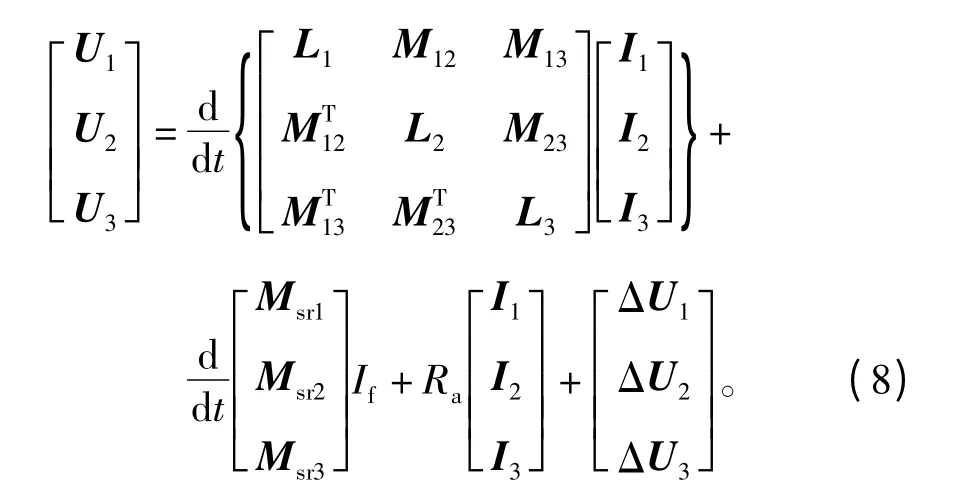
其中，ΔU1、ΔU2和ΔU3是单元电机Y接绕组中点与三相Y接电源中点间的电位差列矩阵。部分单元电机运行时，单元间互感不平衡，每相绕组的阻抗并不完全一致，因此绕组中点与电源中点将存在一个电位差，这一现象在传统三相对称电机系统中并不存在。

由于各单元三相支路电抗不相等，所以部分单元运行时，若采用的是对称三相电压源，则必然会产生三相不对称电流，其定子电流中将含有一定成分的负序分量。同样，假定部分单元电机运行时，各单元三相绕组外接对称三相电流源，则每单元的三相绕组端电压将不再对称。

2 多单元电机的电磁转矩方程

2.1 三相对称电流时的恒定电磁转矩

在此，假定各个单元电机的激励源为幅值相等的三相严格对称的电流源，采用磁共能法计算多单元电机整机运行时的电磁转矩，其转矩矩阵表达式可以写为

式中p为电机的极对数。上述矩阵表达式可以进一步简化为

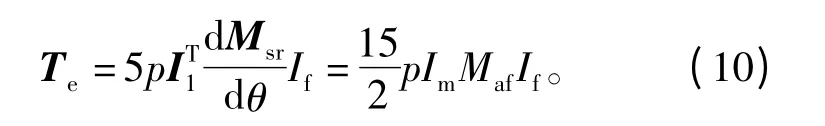
式中:Im是相电流的幅值;Maf是定转子互感的幅值。

仅部分单元电机工作时，仍可用式(9)对转矩进行计算，仅需要将不工作单元的电流矩阵给为0即可。例如，仅1号和3号单元电机运行，则电磁转矩方程可以化简为

对比整机运行与部分单元运行时的恒定转矩表达式可以看出，两单元电机运行时，在相同电流下，其输出电磁转矩是整机运行时的40%。且在同一相电流下，电机对外输出的电磁转矩与运行单元空间位置无关，仅与运行单元数量相关。

2.2 三相对称电流下部分单元运行时的转矩波动

在三相对称电流下，因为单元电机内部及单元电机间的互感不完全对称，所以部分单元运行时，将会引起磁阻转矩波动。该转矩波动主要是由定子绕组互感不对称引起，且该转矩波动数值以及规律不仅与部分单元的运行个数相关，还与运行单元所处的空间排布位置有关。

假设运行的单元电机采用正弦三相对称电流源驱动。当仅1号单元电机独立运行时，其转矩波动可以写为

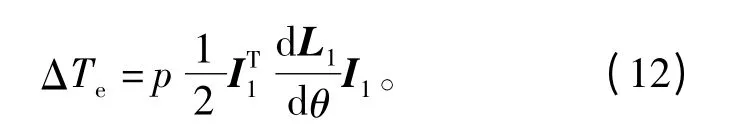
将电感与电流表达式带入公式(12)中，化简后可得一个单元电机运行时的转矩表达式为

从上述表达式中可以看出，一个电周期转矩波动为2次和4次，其幅值与定子绕组电流幅值平方和互感二次波动项的差值成正比。由此也可以看出，在三相对称电流条件下，若多单元电机为严格的隐机电机时，互感不对称并不引起转矩波动，但仍会引起单元电机三相端电压不对称。

与1个单元电机运行类似，空间不同位置的单元电机组合运行时，也含有2次和4次转矩波动，但是其幅值将有所不同。

1#、2#两相邻单元电机运行时转矩波动为

1#、3#两单元电机间隔一个单元运行时的转矩波动为

1#、2#和3#三个单元电机相邻运行时的转矩波动为

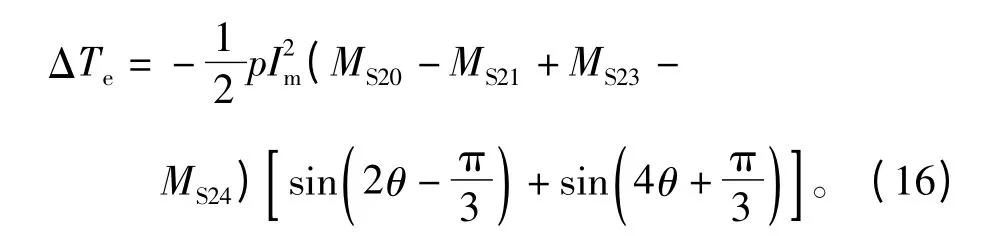
1#、2#以及4#两相邻单元与1个间隔单元电机匹配运行时的转矩波动为

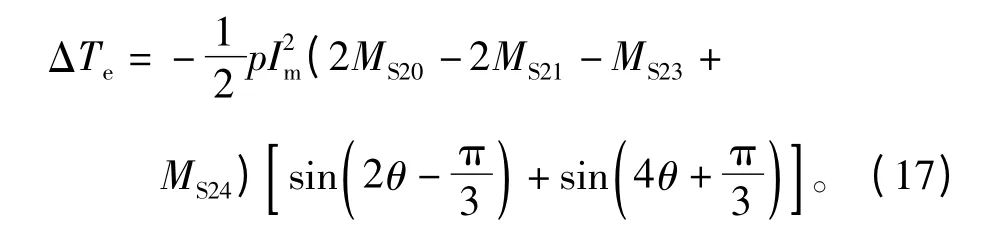
1#～4#四个单元电机运行时的转矩波动表达式与仅1#单元运行时的表达式完全相同，在此不再重复列写。而当所有单元运行时，转矩波动将为零。

绕组间互感二次项随两绕组空间距离的增加而迅速降低，因此转矩波动主要是由相邻两绕组、间隔一相的两绕组的互感二次项之差决定。此外，通过公式可以看出，几个相邻单元电机运行时，其转矩波动与一个单元电机运行时相同，而采用间隔单元运行时，则转矩波动将会增加一倍。在此，采用有限元法，对仅1号和2号单元电机运行的转矩波动进行计算，得到了电流与转矩波动之间的关系，如图3所示。

图3 仅1、2号单元运行时电流与转矩波动曲线Fig.3 Current and torque ripple amplitude relation when No.1 ＆2 unit motors running

从转矩波动计算结果可以看出，2次与4次转矩波动幅值一致，且与相电流成二次函数关系，这与转矩波动解析推导公式相吻合。

3 部分单元运行时转矩波动的抑制

部分单元电机运行时，因为单元内部与单元间绕组互感不对称，而普通三相电机并不含有该类转矩波动。通过计算可知互感不对称引起的波动量为1.26%，试验值为1.55%，因由饱和效应引起的转矩波动尚未计算在内，所以试验数据比计算数据稍大。部分单元电机运行时的2次和4次转矩波动频率较低，对系统的影响尤为明显，所以需要采用一定的抑制转矩波动的措施。

最为直接的是采用谐波电流注入法进行转矩波动抑制，注意到转矩波动为幅值相等的2次和4次波。可分别注入3次和5次正序谐波电流，或1次和3次负序谐波电流，在满足一定幅值、相位条件时谐波电流与基波磁场相作用，即可抵消转矩波动。其中，正序3次电流可抵消2次波动，负序3次电流可抵消4次波动。为得到更为简洁的注入谐波方式，可同时注入正、负序的3次谐波电流。

假定三相绕组激励源为三相对称正弦电流，仅一个单元电机运行，谐波电流引起的转矩波动可表为

经过推导后可知，在满足相位约束条件时的三相正序和负序3次谐波电流合成后的三相电流表达式为

因2次和4次转矩波动的幅值相等，所以正、负序电流幅值也相等，其表达式为

本文计算了一个单元电机运行时，在绕组500 A条件下，注入18 A谐波电流前后的转矩波动曲线，如图4所示。

图4 注入谐波电流前后的转矩波动曲线Fig.4 Inject currents before and after torque ripple curve

通过图4的转矩曲线对比可以看出，转矩波动得到了最大程度的抑制，转矩波动降低了3.5%。此时电机转矩波动中仅含有饱和引起的6次转矩波动成分。当部分单元电机运行时，可以仅选择一个固定单元注入谐波，其余单元仍施加三相对称基波电流。

4 多单元电机相关试验

4.1 单元电机电磁转矩与单元个数关系试验

针对不同单元数量运行，进行相关试验，并与有限元计算结果进行横向对比。计算与试验结果曲线如图5所示。

图5 不同单元运行时的试验与计算数据对比Fig.5 Test and calculation data of different units running

通过图5可以看出，计算数据与试验数据吻合度较高，且随着单元个数增加，同一电流时，整机转矩将成正比增加，转矩数学模型与试验结果相吻合。

4.2 部分单元运行时的转速波动

转矩波动公式的推导是基于三相对称电流源基础之上。因为多单元电机驱动器采用是三相对称电压源，绕组电流将含有三相负序分量，该负序电流将产生2次转矩波动。因样机直接测试转矩波动困难，所以通过测定转速波动来反映转矩波动规律。2 MW样机的转速波动曲线如图6所示。

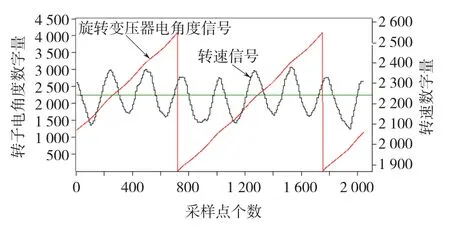
图6 一个单元电机运行时的速度波动曲线Fig.6 Speed ripple of one unit motor running

从图6中可以看出，在一个电周期内，电机的转速波动为4次，该次波动在普通三相电机中是不存在的，而这正是多单元电机的特点之一。

5 结语

本文针对多单元永磁同步电机绕组互感不对称的特殊性，建立了其在自然坐标系下的整机及部分单元运行时的电压方程和转矩方程。分析了在部分单元电机运行时电磁转矩波动的解析表达式，并在此基础之上，给出了采用注入正序、负序3次谐波电流抑制转矩波动的方法，并得到了所需注入谐波电流的解析表达式。数值分析及相关试验表明，本文所推导的多单元永磁同步电机数学模型正确，转矩波动的抑制方法有效。除此之外，上述结论还可用以对不同单元数量的多单元永磁同步电机进行分析。

[1]LEILA P，HAMID A.Five-phase permanent magnet motor drives for ship propulsion applications[J].IEEE Electric Ship Technologies Symposium，2005，12(7):371－378.

[2]向东，于飞.考虑阻尼绕组的五相PMSM数学模型及等效电路[J].电机与控制学报，2008，12(6):644－649.XIANG Dong，YU Fei.Mathematical models and equivalent circuits of five-phase PMSM including damper windings[J].Electric Machines and Control，2008，12(6):644 －649.

[3]MARTIN J，SLOBODAN N Vukosavic，EMIL Levi.Parallel-connected multiphase multi-drive systems with single inverter supply[J].IEEE Transactions on Industrial Electronics，2009，56(6):2047－2057.

[4]欧阳红林，周马山，童调生.多相永磁同步电动机不对称运行的矢量控制[J].中国电机工程学报，2004，24(7):145－150.OUYANG Honglin，ZHOU Mashan，TONG Tiaosheng.Vector control of multi phase permanent magnet synchronous motor with asymmetric structure[J].Proceedings of the CSEE，2004，24(7):145－150.

[5]ZHU Jingwei，NESIMI Ertugrul，SONG Wenliang.Minimum torque ripple current control strategy in a dual fault tolerant PMAC motor drive[C]//2008 IEEE Power Electronics Specialists Conference，June 15 － 19，2008，Rhodes，Greece.2008:1542－1547.

[6]ZHANG Bingyi，LIU Yu，FENG Guihong.Study on low voltage high-power multi-branch permanent magnet synchronous motor[C]//Power and Energy Engineering Conference，March 28－31，2010，Chengdu，China.2010:1－4.

[7]张经纬，祝后权，黄振华，等.多相集中整距绕组感应电机的建模与仿真[J].电机与控制学报，2010，14(9):75－80.ZHANG Jingwei，ZHU Houquan，HUANG Zhenhua，et al.Modeling and simulation of a multiphase concentrated induction Machine[J].Electric Machines and Control，2010，14(9):75 －80.