考虑高频寄生参数继电器EFT干扰机理分析

刘超，王立欣，赵丹

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨150001)

0 引言

电磁继电器是产生电快速瞬变脉冲群(electrical fast transient，EFT)干扰的主要来源[1]。EFT 干扰具备突发、高压、宽频等特征。一旦干扰耦合进敏感设备，会影响整个系统的正常稳定运行[2－3]。

目前，对于继电器触点动作过程的研究主要集中在对继电器设计[4－6]及其电弧特性的研究[7－11]。文献[5]运用传输线理论及部分元等效电路法对继电器本体分布参数进行提取，并分析了继电器瞬态干扰的辐射性能。文献[6]分析了工频磁场对继电器动态特性的影响。文献[9－11]分析了不同条件下继电器断开过程中的电弧特性。对宏观瞬态干扰特性的研究只是基于火花放电理论获得的一些定性分析结论[12－15]而对EFT宽频干扰形成机理及其特性的研究还未见报道。

本文通过引入集总高频等效参数的分析方法建立继电器触点断开感性负载瞬间电接触动态模型，分别对触点断开过程中金属弧、气体击穿区以及振荡区等三个主要阶段进行求解，分析各主要参数对EFT干扰特性的影响。从而为研究电磁继电器断开感性负载时，EFT干扰的产生机理及特性提供理论基础。

1 传统分析方法与实验对比

传统分析方法建立在火花放电理论基础上[16－17]。其等效电路模型如图1所示。其中，C0为全电路等效杂散电容。开关断开时，电感L中能量没有泄放通路，电流流向杂散电容C0，对其进行反向充电，使其出现暂态过电压，当触头两端电压高于继电器触头间介质击穿电压时，便形成击穿电弧，使开关触点重新导通，C0放电，当电流小于维持电流时，触头间的电弧熄灭。上述过程重复发生，直至电容两端电压不能使开关动、静触头击穿为止。其典型暂态过程如图2所示。

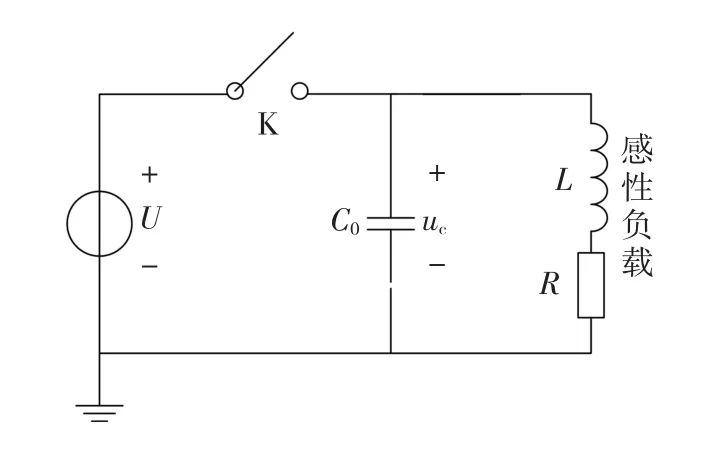
图1 继电器断开感性负载时等效电路模型Fig.1 Equivalent circuit of relay shutting down inductive load

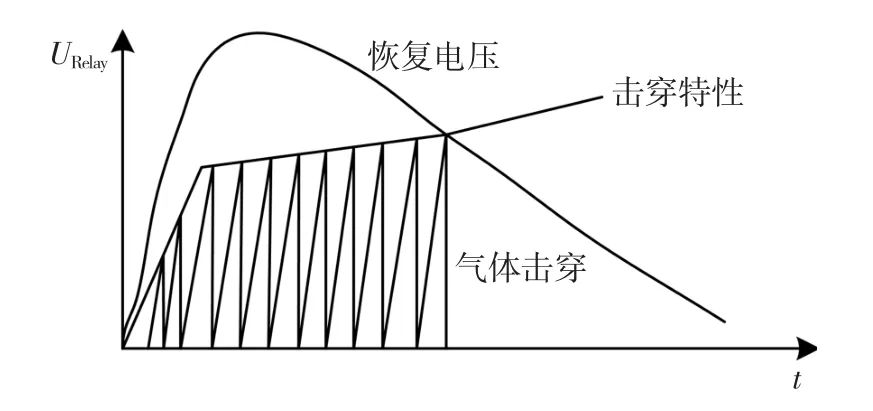
图2 典型暂态过程示意图Fig.2 Diagram of the transient process

根据电感线圈中电流值可以计算分断开关引起的EFT电压。由基尔霍夫电压定律，其二阶微分方程为

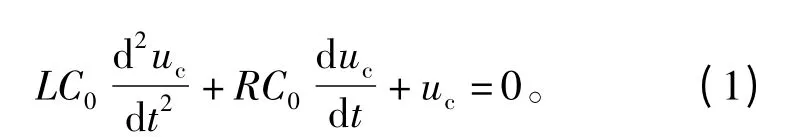
经推导，则杂散电容C0两端的暂态电压为

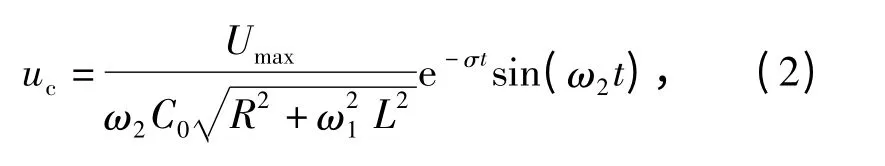
式中:ω1为电源电压U的角频率，ω2称为自由谐振角频率，σ称为衰减系数，Umax为电源电压最大值。

这种传统分析方法只能从宏观角度定性分析触点两端产生过电压并击穿空气产生振荡的过程。而在电磁继电器分断感性负载的瞬态击穿实验过程中发现，实际的断开过程要更为复杂。

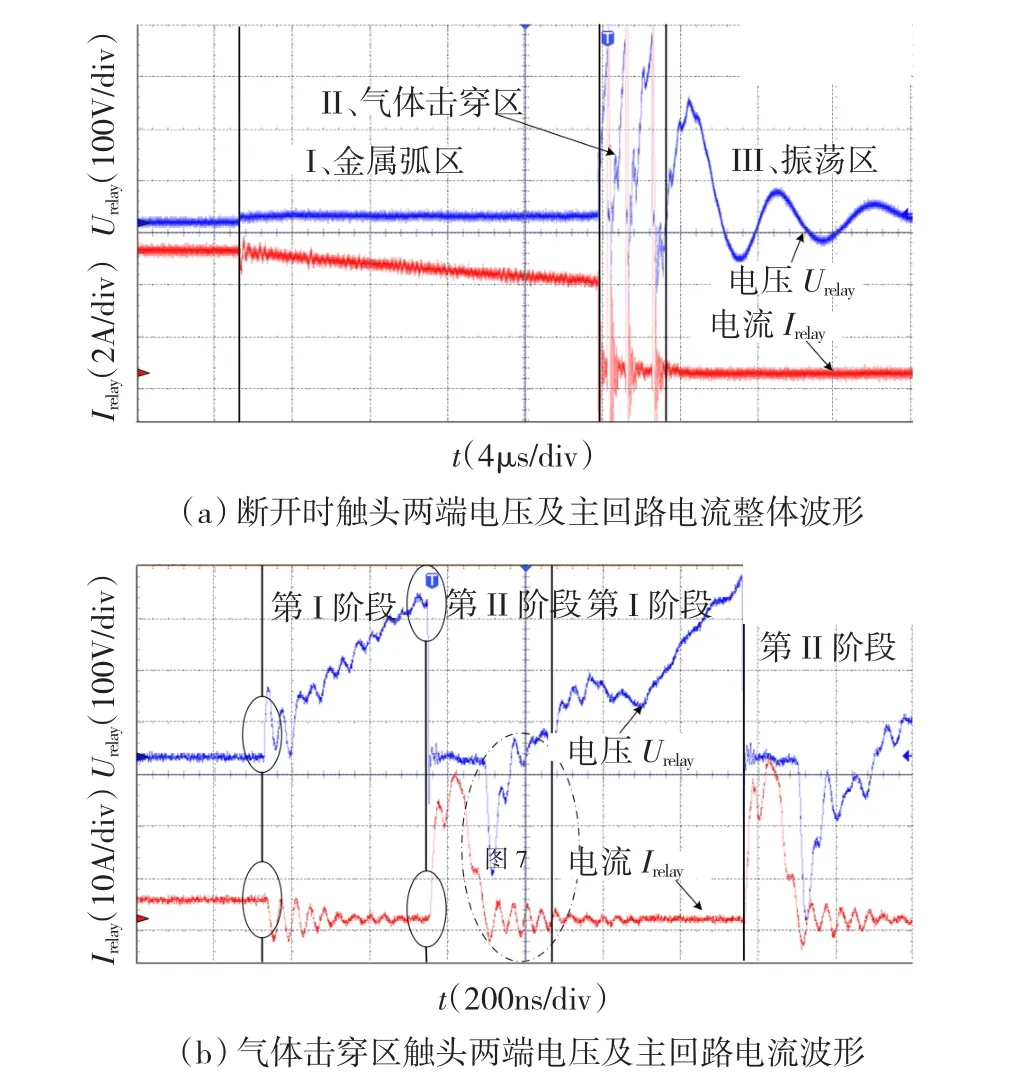
图3 断开瞬间触头两端电压及主回路电流波形Fig.3 U and I waveforms during the shutting down process

为反映上述事实，对继电器断开感性负载时产生的EFT干扰进行了实测，电路如图1所示，电源电压U=10 V，采用HRS4H－S－DC12V型镀金触点继电器。电感为1.78 mH。导线长度5 m。电阻为0～50 Ω可调功率电阻。如图3(a)、图3(b)所示为继电器触头两端电压及主回路电流波形，这一波形与文献[12]中给出的结论吻合。可以将这一过程分为三个阶段，即金属弧区、气体击穿区、振荡区。

真实工况下继电器断开感性负载时产生的EFT干扰，其高频分量占有很大的比例。对图3数据进行频谱分析，按传统方法得到的气体击穿区电压、电流的基频频率在2.5 MHz以内，而由高频寄生参数引起的，在基频基础上叠加的最高干扰频率可达200 MHz以上，其中2.5～200 MHz的宽频范围能量占总能量的36.7%。这些高频干扰更容易耦合进敏感设备，对它的抑制又往往比较困难。其次，传统分析方法无法解释在气体击穿区的第二阶段继电器触点两端产生负向电压的原因。这就需要建立更加精确的分析模型。

下面就针对这一情况，在火花放电理论的基础上，采用引入集总高频等效参数的方法对整个触点断开的瞬态过程进行建模，并分析其干扰产生机理。

2 考虑寄生参数的EFT产生机理分析

2.1 金属弧形成机理

从微观角度看，触点表面粗糙，流过的电流集中在某些点上。分断开始时，接触压力不断降低，实际接触面积不断减小，使得接触电阻增加。电流不变时，焦耳热不断增加。另一方面，由于此时已分离点之间间隙小，触点间的电场强度高，在电场力的作用下，使得阴极某些点放出电子，这些电子轰击阳极，使阳极金属原子电离产生正离子。而间隙中的游离金属也可能被轰击成正负离子。这些离子加强了间隙中的电场强度，引起更多电子发射，形成电弧放电，放电使得电极表面温度急剧升高。在上述两方面原因的作用下，使触点材料熔化形成金属桥。电流在金属桥中间流过，从而形成金属弧[18]。

金属弧电压仅由触头的材料决定，近似为一个常数，文献[19]通过实验证明得出结论，最小电弧电压Ugap仅由材料的有效逸出功和电离电势决定。而金属弧电阻RK以一定斜率k上升，斜率k与初始电流I0有关。金属弧持续时间t也是与初始电流I0相关的值。初始电流越大持续时间越长。通过实验得到的数据可以拟合出斜率k和金属弧持续时间tm的曲线如图4所示。用式(3)来描述触点处在金属弧区间内的电接触特性。

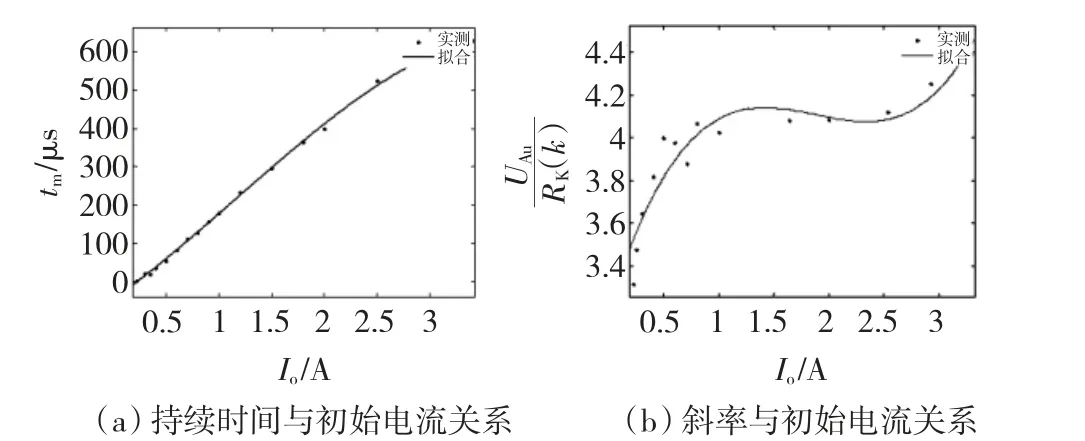
图4 金属弧持续时间、斜率与初始电流函数关系拟合图Fig.4 Diagram of tm and k vs.Io

在0＜t≤tm时，有

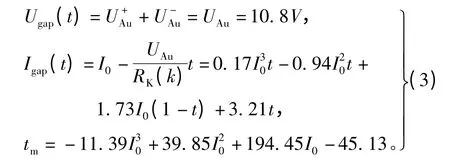
2.2 气体击穿区形成机理

气体击穿区从金属弧区结束开始，每一次击穿可分解为I、II两个阶段。由于继电器开关触点断开瞬间，产生的EFT干扰频谱范围极宽，可以达到数百兆，所以在分析过程中需要考虑到器件的高频特性及电路的寄生参数。图5所示，为考虑了高频寄生参数的电路模型。其中Rs为电源内阻，CKpar为继电器触头之间的寄生电容，Rload为负载电阻，Lload为负载电感，Llead、Clead分别为负载电感引线的电感、电容，CLpar、Rpar分别为负载电感的寄生电容、电阻，Cpar、Lw是电路导线及其它除电感部分外的等效寄生电容、电感。

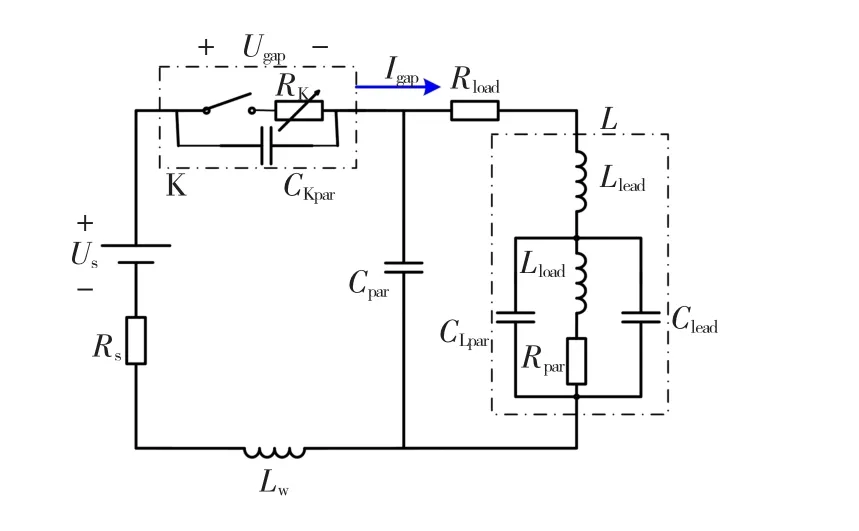
图5 气体击穿区等效电路模型Fig.5 The equivalent circuit for the gas breakdown section

简化和等效:为了方便分析，可以做等效和简化，即将CLpar与Clead合并为C'Lpar。对于电感而言，由于导线的寄生电感为0.92 μH，是主电感值(1.78 mH)的1/1 935，根据文献[20]可知，可以忽略 Llead的作用，则电路图可以简化为如图6所示。同时，由图3实线圈标注处得知:每一阶段动作前一瞬间电压、电流变化率远远小于动作后一瞬间电压、电流变化率。所以，在分析过程中，忽略动作前由于电压、电流变化率引起的电容电压和电感电流。

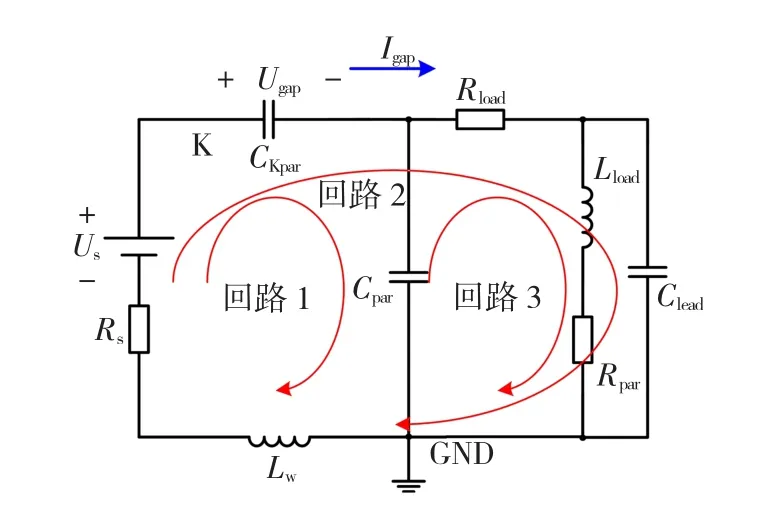
图6 简化后的等效电路模型Fig.6 The simplified equivalent circuit

下面就每次击穿中的两个阶段来讨论气体击穿区的形成机理。

第I阶段:如图3(b)所示，为金属弧结束到气体击穿前。在这个阶段中，开关触点两端电压上升机理与传统分析方法相同，详见第1部分。下面主要分析考虑到寄生参数 Lw、CKpar、Cpar等的影响在电压中叠加的高频振荡分量特性。如图6所示，对回路1列写回路电压方程。此处只分析高频振荡分量的小信号特性，故忽略负载电感 Lload对 Cpar的影响。所以有

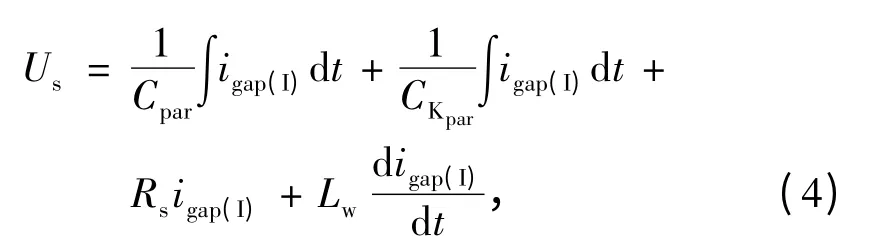
式中igap(I)为一阶段流过触点的电流。整理得到二阶齐次微分方程为

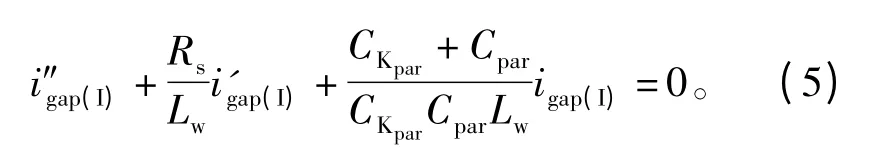
又因为其初始条件为

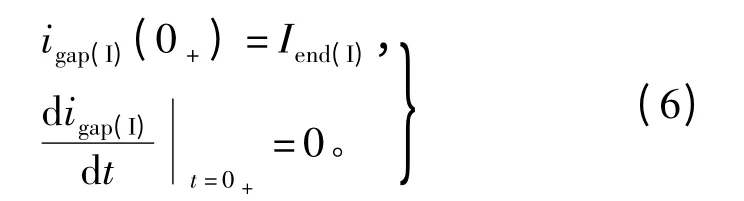
式中Iend(I)为金属弧结束时，主回路电流值。

推导过程中，根据实际情况分析，电源内阻Rs取值 0.51Ω，Lw为微亨级 10－6H，Cpar、CKpar为纳法级10－12F，所以有

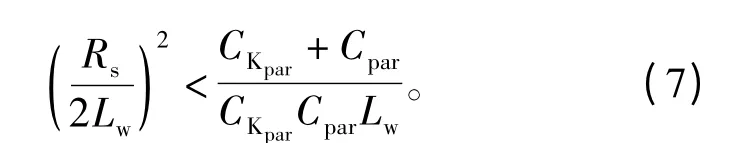
则齐次微分方程有两个共轭复数根。求解方程得到

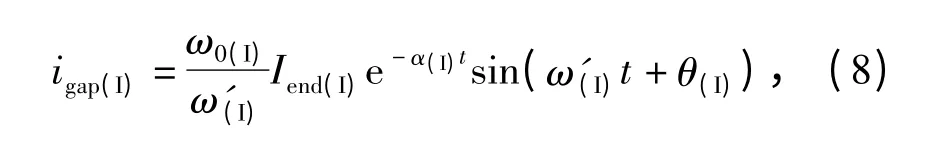
由上式可见，电流为阻尼振荡变化。其衰减系数由寄生电感Lw与电源内阻Rs共同决定，内阻越高，寄生电感越小则衰减越迅速。高频振荡频率由电感Lw、寄生电容Cpar和触头寄生电容 CKpar共同决定，且随着寄生参数的减小而升高，也就是说此时的寄生电容、电感越小时，则电路中产生振荡的频率越高。振荡的初始值除了由上述这些寄生参数决定外，还取决于金属弧结束时的主回路电流 Iend(I)，Iend(I)越大则初始振荡幅值越大。

第II阶段:为气体击穿后到击穿电弧熄灭，触点电压恢复正值前。如图6所示，当继电器触点间的气体被电压击穿后，认为继电器处于导通状态，等效为一个微小电阻。此时，电容Cpar中存储的能量通过主回路流回电源Us，如图3(b)所示，主回路中出现较大的放电电流，触点两端电压维持在0 V左右。当电容放电结束后，电路进入谐振阶段。此时，认为继电器重新关断，重新等效为电容CKpar。电容Cpar与电感Lload能量在彼此之间流动，对主回路不产生影响，故谐振主要是由CKpar、Lw与CLpar引起的。

根据上面的分析，对回路2列写电压方程为

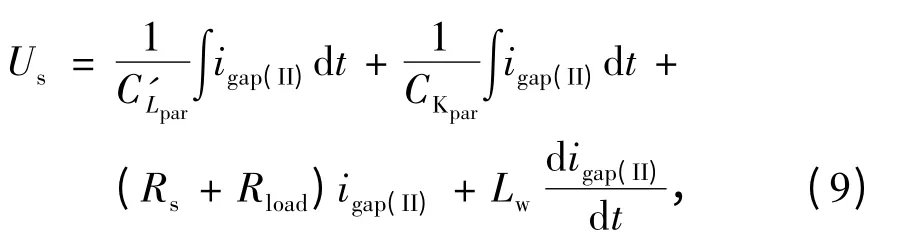
式中igap(II)为二阶段流过触点的电流，整理得到

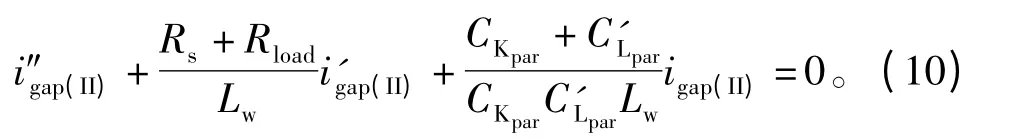
其初始条件为

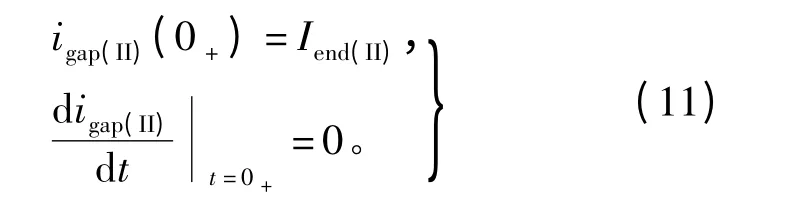
式中Iend(II)为第一阶段结束时，主回路电流值。求解方程得到

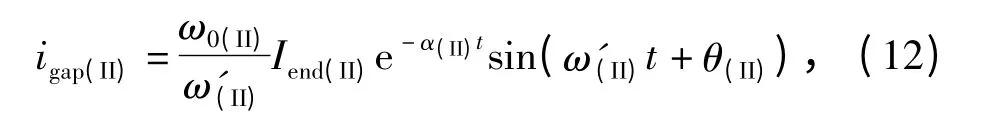
由上式可见，衰减系数和振荡频率特性与第I阶段相似，此处不再分析。而振荡的初始值除了与寄生参数有关外，还与负载的电阻值相关，负载电阻值越大时则振荡的初始值越高。将图3(b)中虚线部分放大，如图7所示，为这一过程的细节波形。当主回路电流值小于零时，对电容 CKpar反向充电，则继电器触点两端电压值下降，此时在继电器触点两端产生了负向电压。当主回路电流值大于零时，对电容Cpar正向充电，则触点电压值上升。

继电器触点两端产生负向电压这一现象运用传统方法分析时是无法解释的，而采用本方法可以很好的对其进行解释。

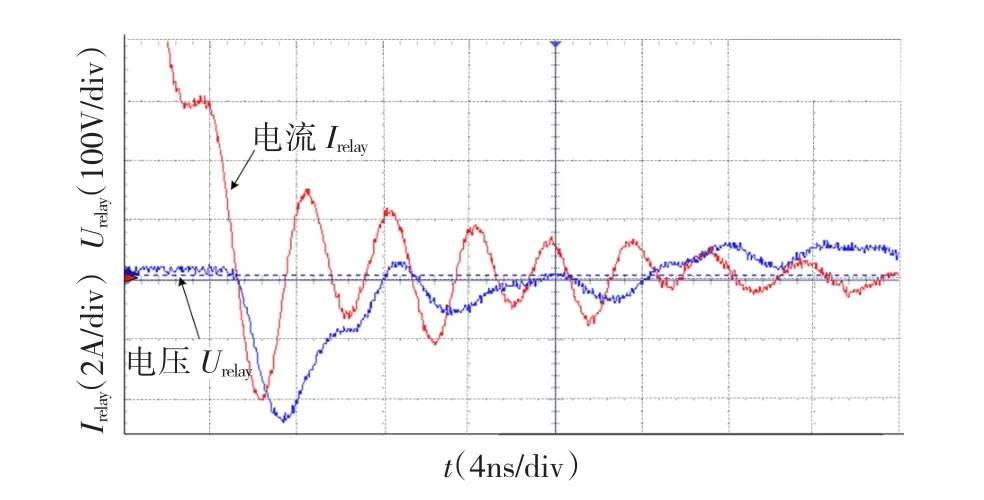
图7 气体击穿区第二阶段局部电压电流细节图Fig.7 U and I partial waveforms of the breakdown section

2.3 振荡区形成机理

气体击穿区结束后，电感仍然有一部分能量无处泄放，而此时加在继电器触点两端的电压又不足以将空气击穿。所以，这部分能量在电感Lload和寄生电容Cpar之间流动，在继电器触点两端形成了周期振荡的电压。此时主回路中无电流流过。

同样对回路3列写电压方程为

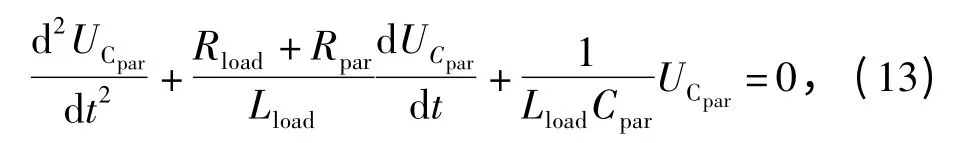
式中UCpar为继电器触点两端电压值，其初始条件为

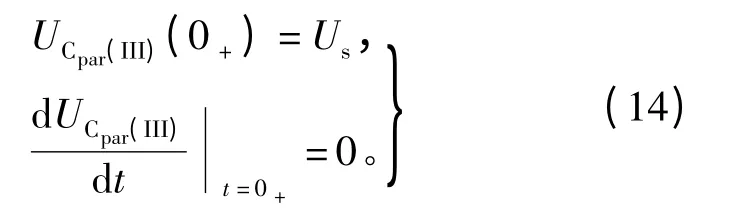
解得

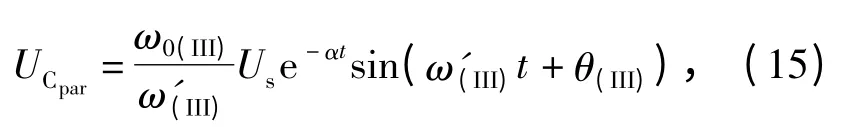
振荡区为衰减振荡过程，幅值与电源电压寄生参数，负载电阻有关，衰减系数和振荡周期由负载电感Lload、主寄生电感Cpar以及负载电阻Rload等参数决定。

3 参数影响分析

针对前述推导结论，主要针对对EFT干扰高频分量影响比较大的参数 Iend、CKpar、Lw进行实验，从而验证模型的正确性。首先，分析金属弧结束时电流Iend(I)对气体击穿区高频振荡电流幅度的影响。在 Iend(I)分别为 220 mA，240 mA，280 mA 时，分别截取高频振荡电流波形。主回路电流振荡幅度如图8所示，将电流振荡幅值列入表1中。可见当金属弧结束电流越大时，击穿区高频振荡电流的峰值也越大。从表中可以看出振荡电流峰值并非与这与Iend(I)成线性正比关系，这是由于 Iend(I)的变化取决于继电器开关的动作速度，这一速度会影响继电器两端等效电容CKpar与金属弧结束时间。这两个参数又会影响到高频振荡幅值的大小。但从表中可以看出振荡电流与Iend是成正比关系的，这与前面的推导结论是一致的。

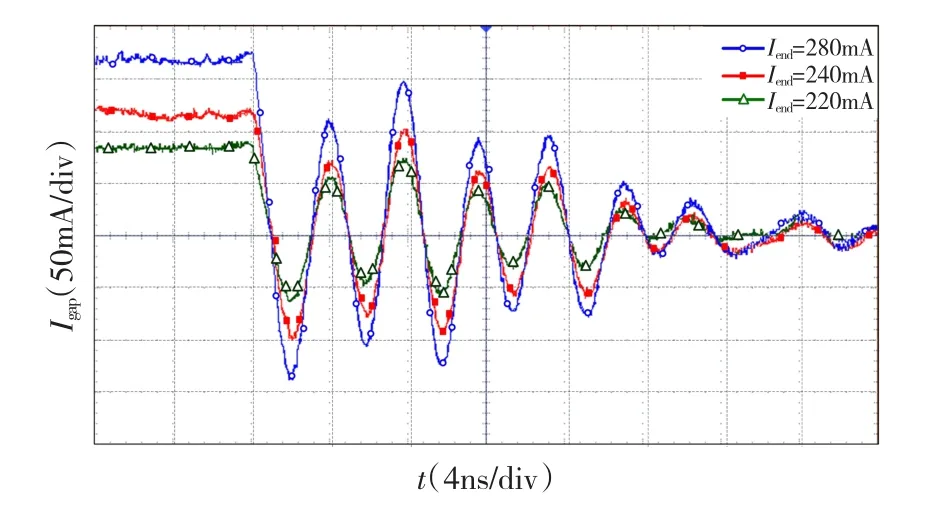
图8 Iend(I)对电流振荡峰值的影响Fig.8 The influence of Iend(I)to oscillation current peak value

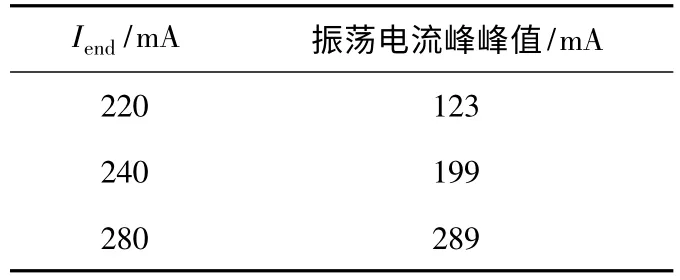
表1 Iend(I)与高频振荡电流幅值关系表Table 1 The relationship between Iend(I)and the HF current

其次，分析继电器两端寄生电容CKpar对气体击穿区高频振荡电流的影响。由于CKpar是寄生参数，无法直接改变这一参数的大小。所以采取在继电器两端添加一小电容Cadd的方法来模拟继电器寄生电容的变化。分别当不添加电容，添加330 pF电容，添加470 pF电容时，分析对电流振荡频率的影响。如图9及表2所示，不添加电容时，其振荡电流频率达到54 MHz，这样的高频干扰一旦向空间辐射是很难抑制的。当加入470 pF电容后，其振荡频率减小为4.4 MHz，降低为原来的8%。虽然高频电流振荡幅值提高了8 mA，但由于频率的大幅降低。这与前面推导的结论相吻合。

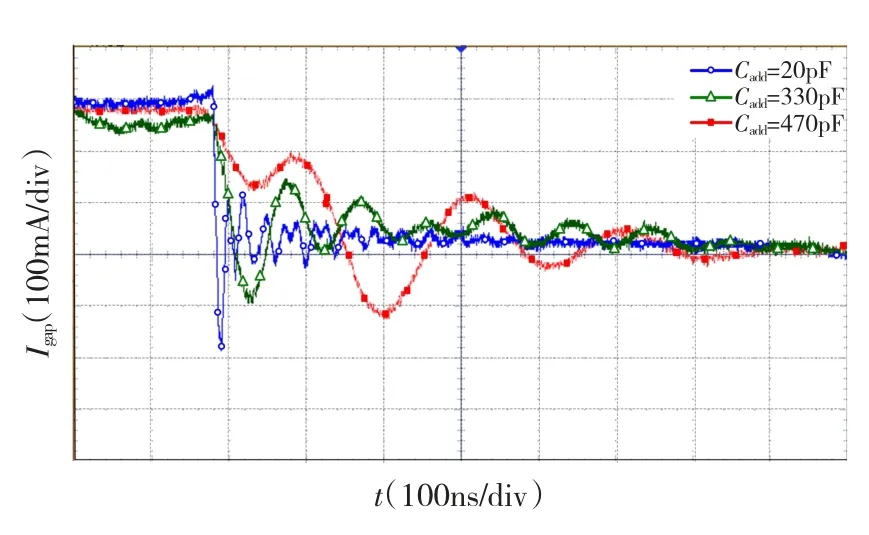
图9 Cadd对电流振荡频率的影响Fig.9 The influence of Cadd to the oscillation current frequency

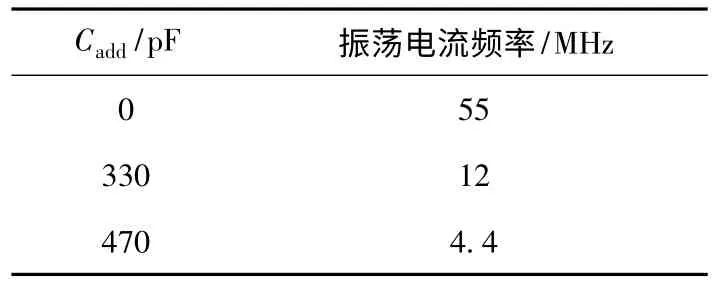
表2 Cadd与高频振荡电流频率关系表Table 2 The relationship between Cadd and the f of HF current

最后，分析电路中寄生电感Lw对高频振荡电流频率的影响。同样采取延长主回路导线的长度模拟主回路中寄生电感发生变化时对气体击穿区电流振荡频率的影响。分别当不增加导线长度，添加20 m导线长度，添加40 m导线长度时，分析对电流振荡频率的影响，如图10及表3所示。

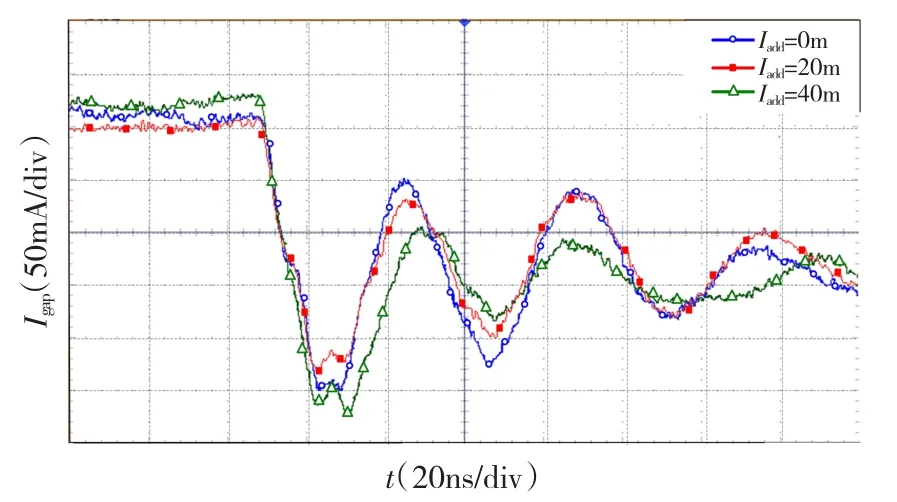
图10 Ladd对电流振荡频率的影响Fig.10 The influence of Ladd to the oscillation current frequency

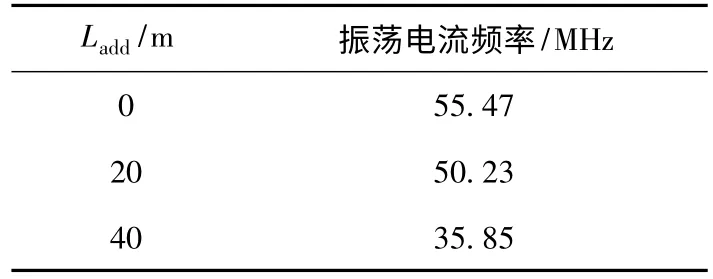
表3 Ladd与高频振荡电流频率关系表Table 3 The relationship between Ladd and the f of HF current

当延长导线40 m时，电路中高频振荡电流的频率相比没有延长电缆时下降了35.4%，而且幅值也下降了39 mA，这样即达到降低干扰频率，又降低干扰幅值的效果。所以在实际应用过程中，可以采取延长在主回路中加入一个小电感的做法来降低EFT干扰的辐射作用。

4 结语

本文在原有火花放电理论基础上，针对电磁继电器断开感性负载过程中，EFT干扰的宽频特性，提出了引入集总高频等效参数的分析方法。对触点断开过程中金属弧区，气体击穿区以及振荡区等三个阶段进行了求解，考虑高频寄生参数对EFT干扰宽频特性的影响，建立了能够反映电磁继电器触点断开感性负载过程中的瞬态电接触动态数学模型。并运用该模型解释了在气体击穿区第二阶段继电器触点两端产生负向电压这一特殊现象。最后，通过包括金属弧结束电流Iend、寄生电容CKpar、寄生电感Lw在内的多组实验分析了主要参数对EFT干扰特性的影响提出了从原理上来抑制EFT干扰的方法，并且验证了模型的正确性。

[1]孙亚秀，孙睿峰，陈炳才.三相PWM变换器传导干扰的预测分析[J].电机与控制学报，2011，15(5):42 －48.SUN Yaxiu，SUN Ruifeng，CHEN Bingcai.Forecast of conducted interference of three-phase PWM drive motor system [J].Electric Machines and Control，2011，15(5):42 － 48.

[2]汪泉弟，秦传明，郑亚利，等.低压永磁直流电机的传导电磁干扰模型[J].电机与控制学报，2011，15(1):55 －59.WANG Quandi，QIN Chuanming，ZHENG Yali，et al.Conducted EMI model for the low-voltage permanent magnet DC motor [J].Electric Machines and Control，2011，15(1):55 －59.

[3]MUSOLINO F，FIORI F.Invstigations on the susceptibility of ICs to power-switching transients[J].IEEE Transactions on Power E-lectronics，2010，25(1):142 －151.

[4]翟国富，王其亚，程贤课，等.电磁继电器动态特性快速算法及其在优化中的应用[J].中国电机工程学报，2010，30(12):106－110.ZHAI Guofu，WANG Qiya，CHENG Xianke，et al.Fast algorithm of dynamic characteristics of electromagnetic relay and its application on optimization[J].Proceedings of the CSEE，2010，30(12):106－110.

[5]翟国富，王新宇，楚兵.基于等效电路法的高频继电器建模与研究[J].中国电机工程学报，2009，29(15):119 －124.ZHAI Guofu，WANG Xinyu，CHU Bing.Modeling and study of high frequency relay based on equivalent circuit method[J].Proceedings of the CSEE，2009，29(15):119 －124.

[6]杨文英，任万滨，翟国富，等.工频磁场对电磁继电器动态特性影响的三维有限元分析[J].电工技术学报，2011，26(1):51－56.YANG Wenying，REN Wanbin，ZHAI Guofu，et al.3-D finite el-ement analysis of dynamic characteristics of electromagnetic relay inter fered by power frequency magnetic field[J].Transactions of China Electrotechnical Society，2011，26(1):51 －56.

[7]ZHAI Guofu，FAN Weiwei，WANG Hailong.Research on dynamic characteristics of the electromagnetic relay[C]//IEEE International Conference on Mechatronics and Automation，August 5 － 8，2007，Harbin，China.2007:2763 －2767.

[8]周玮，臧春燕，何俊佳.电气参数和机械参数对继电器直流电弧的影响[J].中国电机工程学报，2006，26(19):151 －155.ZHOU Wei，ZANG Chunyan，HE Junjia.Influence of electric and mechanism parameters on DC arc in relays[J].Proceedings of the CSEE，2006，26(19):151 －155.

[9]吴翊，荣命哲，王小华，等.触头打开过程中低压空气电弧等离子体的动态过程[J].电工技术学报，2008，23(5):12 －17.WU Yi，RONG Mingzhe，WANG Xiaohua，et al.Dynamic analysis of low-voltage air arc plasma during contact opening process[J].Transactions of China Electrotechnical Society，2008，23(5):12 －17.

[10]KHARIN S，NOURI H，BIZJAK M.Effect of vapour force at the blow-open process in double-break contacts[J].IEEE Transactions on Components and Packing Technologies，2009，32(1):180－190.

[11]ZHAI Guofu，ZHOU Xue.Study on arc generated by opening electromagnetic relay contacts in DC low-current resistive circuit with constant velocity[J].IEICE Transaction on Electronics，2008，E91C(8):1233 －1239.

[12]MAKOTO H，YOSHINOBU K.An experimental study on minimum arc current for arcs longer than a few microseconds in relay contacts and possible reinterpretation of the meaning thereof[J].IEEE Transactions on Components and Packaging Technologies，2009，32(1):127 －134.

[13]陈嵩，沙斐，王国栋.电气化铁道脉冲电磁骚扰的 Simulink模型[J].铁道学报，2009，31(1):55 －58.CHEN Song，SHA Fei，WANG Guodong.Modeling and simulating impulse RF noises of electrical railways in Simulink environment[J].Journal of the China Railway Society，2009，31(1):55－58.

[14]HONMA H，KIMURA S，SHOJI K，et al.Arc discharge and surge suppression during a breaking operation of a magnetic relay[C]//The 53rd IEEE Holm Conference on Electrical Contacts，September 16－19，2007，Pittsburgh，USA.2007:280－283.

[15]WAKATSUKI N，YONEZAWA Y.Relay contacts of multi-electrodes with timely controlled operation for arc discharge suppression[C]//Proceedings of the 50th IEEE Holm Conference on E-lectrical Contacts，September 20 － 23，2004，Tokyo，Japan.2004:474－479.

[16]王玉峰.变电站瞬态电磁环境及微机保护系统 EMC研究[D].大连:大连理工大学电机与电气，2007:15－36.

[17]秦晓辉，黄少锋.保护与控制二次回路内电快速瞬变脉冲群的干扰模型及 MATLAB仿真[J].继电器，2006，34(4):17－21.QIN Xiaohui，HUANG Shaofeng.Modelling of EFT interference in protect and control secondary loop using MATLAB[J].Relay，2006，34(4):17 －21.

[18]SUHARA K.Analysis of metallic phase arc duration at a break contact with the use of weibull distribution method[C]//Proceedings of the 43 IEEE Holm Conference on Electrical Contacts，October 20 －23，1997，Philadelphia，USA.1997:175 －182.

[19]徐金玲.继电器触头燃弧时间分析及其试验[D].武汉:华中科技大学高压与绝缘技术，2007:56－75.

[20]PAUL C.电磁兼容导论[M].2版.闻映红，译.北京:人民邮电出版社，1998:226－235.