“守恒法”在力学中的应用

刘俊娟

(河北师范大学附属民族学院 河北 石家庄 050083)

赵 强

(石家庄机械化步兵学院 河北 石家庄 050083)

魏增江

(石家庄理工职业学院 河北 石家庄 050083)

守恒定律是关于过程的规律,阐述的是,只要过程满足一定的条件，就可以不必考虑过程中的细节而对系统在过程中的任意两个状态(包括始、末状态)的某些特征下结论.不追究过程的细节而能对系统的状态下结论，这是守恒定律的特点，也是守恒定律的优点，因而,在物理学中分析问题常常应用守恒定律.

(1)天车上悬吊的冲击摆[1]

【例1】质量为M1的天车，静止在光滑水平轨道上，车的底部系有两根等长的细绳，绳的长度为l，质量可忽略，两绳的下端挂有一质量为M2的砂袋.今有一质量为m的子弹水平射入砂袋并留在袋中与袋一起运动.已测出砂袋摆过的最大角度为θ.求子弹的入射速度.

解析：图1表示子弹入射到砂袋摆过最大角度的示意图.下面应用守恒方法求解.

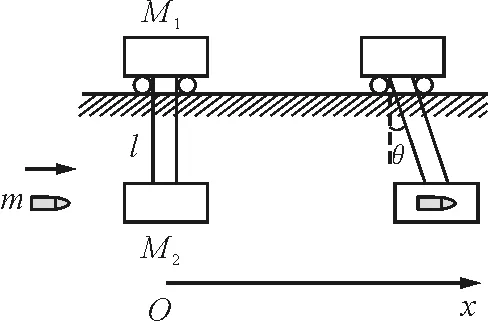
图1

分析子弹m射入砂袋M2的过程.对子弹和砂袋构成的系统，因子弹与砂袋间的内冲力远大于绳对砂袋的拉力的水平分力，故系统水平方向动量近似守恒，取坐标Ox水平向右，有

mv0=(m+M2)v1

(1)

式中，v0为子弹的入射速度，v1为子弹相对砂袋刚静止的瞬时子弹与砂袋的共同速度.

在天车向右运动同时砂袋上摆的过程.对于子弹、天车、砂袋系统，因绳对砂袋及天车的拉力(外力)在水平方向的合力为零，故系统水平方向动量守恒.又因砂袋摆到最高点时砂袋、天车具有相同速度v2，所以有

(m+M)v1=(m+M1+M2)v2

(2)

同一过程，对子弹、天车、砂袋、绳子和地球构成的系统，因满足条件外力做功之和

A外=0

非保守内力做功之和

A非保内=0

故系统机械能守恒.有

(m+M2)gl(1-cosθ)

(3)

联立式(1)、(2)、(3)可解得

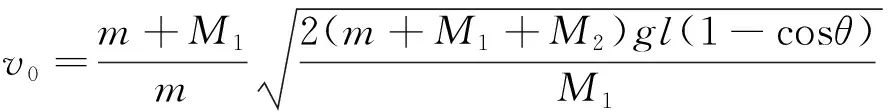
(4)

(2)被子弹击中的弹簧连接体

【例2】如图2所示，质量均为m的两物体A和B都静止在光滑水平面上，用劲度系数为κ的轻弹簧连接.一质量为m的子弹C以水平速度v0击中物体A并留在A内.求：

1)弹簧的最大压缩量；

2)物体B的最大动能及物体A的最小动能.

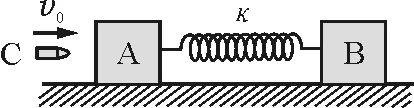
图2

解析：1)子弹射入物体A的过程，对子弹、物体A组成的系统，因为弹力远小于内冲力，所以系统动量近似守恒.设子弹射入物体A后在A内停止运动瞬时，物体A的速度为vA，取坐标水平向右，由动量守恒有

mv0=(m+m)vA

又因子弹与物体A碰撞时间极短，在这段时间内弹簧尚未被压缩，所以碰后物体B瞬时速度vB=0.

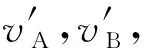
当弹簧压缩量最大时，应有

联立上式求解得

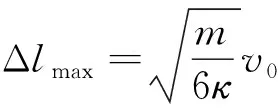
(5)

2)当物体B动能最大时，弹簧压缩量为零，又由于上述过程，物体A(包括子弹)，物体B及弹簧系统机械能守恒，因而，物体B动能最大时，必有物体A动能最小.因此，将Δl=0代入上述守恒方程，即可解得

所以

(6)

(3)转台问题[2]

【例3】一质量为m的小孩，站在一半径为R,转动惯量为J0的静止水平转台的边缘上，此转台可绕通过转台中心的竖直轴转动，转台与轴间的摩擦不计.如果此小孩相对转台以v的速率沿转台边缘行走，问转台的角速度有多大？

解析：小孩与转台作为一定轴转动系统，人与转台之间的相互作用力为内力，且沿竖直轴方向不受外力矩作用，故系统的角动量守恒.在应用角动量守恒时，必须注意人和转台的角速度ω，ω0都是相对于地面而言的，而相对于转台的角速度ω1应满足相对角速度的关系式

ω=ω0+ω1

由相对角速度的关系，人相对地面的角速度为

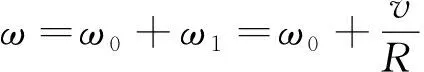
(7)

由于系统初始时是静止的，根据系统的角动量守恒定律，有

J0ω0+J1(ω0+ω1)=0

(8)

式中J0,J1=mR2分别为转台、人对转台中心轴的转动惯量.由式(7)、(8)可得转台的角速度为

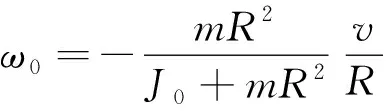
(9)

式中负号表示转台转动的方向与人对地面的转动方向相反.

以上例题的解析，表明守恒法在力学中应用很广泛.这是因为有些问题虽然其过程很复杂，但不论系统内部发生了多少复杂的变化，只要守恒条件成立，守恒定律就可以应用.守恒定律不仅在宏观领域可以应用，在微观领域也可以应用.例如，绝大部分的“基本”粒子就是通过守恒定律的应用而发现的[3].所以，应用守恒定律处理问题，不但对于求解物理习题，而且对于一般科学研究都是十分重要的方法.

参考文献

1 康颖. 大学物理(新版)第一版.北京：科学出版社，2005

2 张三慧.大学物理学.北京：清华大学出版社，2004

3 马文尉.物理学教程.北京：高等教育出版社，2007