海底管道砂袋堆叠防护效果数值模拟

于俊峰

胜利油田海洋采油厂，山东东营 257237

海底管道是海上油气运输最主要的方式之一，有着便捷、经济和运输量大等优点。海底管道处于海底复杂多变的危险环境中，其安全性和稳定性难以保证[1-2]。管道悬空是海底管道面临的安全风险之一，为此提出了多种海底管道防护措施，其中抛填砂袋是海底管道悬空的主要治理措施。但堆叠的砂袋易出现倒塌和被海流冲走等问题，从而导致管道失效，例如，平湖油气田海底输油管道岱山登陆段虽定期进行砂包回填加固，但仍不能有效杜绝管道悬空，呈现“悬空-回填-冲刷-出露-悬空”的恶性循环[3-5]。因此，有必要研究如何避免砂袋被冲走。本文以渤海某海底管道悬空治理案例中砂袋堆叠形式为研究对象，运用Fluent软件建立二维流场模型，分析不同形式砂袋堆叠周围流场分布及变化规律，旨在通过优化砂袋堆叠的形式来降低砂袋被冲走的风险。

1 控制方程组的建立

假设海流流速恒定，基于κ-ε湍流模型的二维流场模型，涡黏性系数由湍动能κ和湍动能耗散率ε来确定，其流动方程为：

式中：ui、uj（i=1，2；j=1，2） 为流体速度，m/s；xi、xj（i=1，2；j=1，2） 为坐标系，x1、x2分别代表x、y坐标；t为时间，s；ρ为流体密度，kg/m3；p为静压，Pa；μ为流体运动黏性系数；μt为湍流黏性系数，μt=Cμκ2/ε （Cμ为常数，取0.09）；Gκ为中间变量，Gκ= μt（∂ui/∂xj+ ∂uj/∂xi）∂ui/∂xj；σκ、σε、C1ε、C2ε为常数，取 σκ=1.0、σε=1.3、C1ε=1.44、C2ε=1.92。

2 边界条件及网格划分

渤海某海底管道悬空治理案例采用砂袋堆叠堤坝形式保护海底管道。本文将该保护形式简化为二维模型（见图1），采用标准κ-ε湍流模型，并用更适合求解黏性底层和过渡层的低雷诺数κ-ε模型来模拟流体流动[6-10]。速度入口边界参考渤海平均潮流速度，入口速度设置为0.5 m/s，海床面及砂袋表面壁面粗糙度设置为默认值0.5，为防止流体受到顶面壁面的摩擦作用而影响流场分布，顶面设定无摩擦壁面，即壁面粗糙度为0，出口设置为压力出口边界条件。利用ICEM软件对计算区域进行网格划分，采用适应性较好的非结构性网格，且为满足数值计算精度与稳定性，网格的最大尺寸设为0.1 m。在海床面和砂袋表面区域进行边界层划分并加密，最终将划分好的网格导入Fluent中进行计算。

图1 砂袋堆叠二维模型示意

3 结果分析

3.1 砂袋堆叠倾角对流场的影响

选用渤海某海底管道悬空治理案例的砂袋堆叠形式为例（顶宽3 m、底宽12 m、高度1.5 m、倾角18.4°），当确定砂袋堆叠倾角、砂袋堆叠顶宽和砂袋堆叠高度的数值时，可以确定砂袋堆叠截面形式，从这三个方面来分析砂袋堆叠形式对流场的影响[11]。取砂袋堆叠顶宽为3 m、高度1.5 m，且保持顶宽、高度皆不变，倾角分别为14.0°、18.4°、23.2°、26.6°、45.0°，其底宽相应变化，依次为15、12、10、9、6 m，模拟计算不同堆叠倾角时（见图2）砂袋堆叠周围流场分布变化，分析砂袋堆叠倾角对流场的影响。

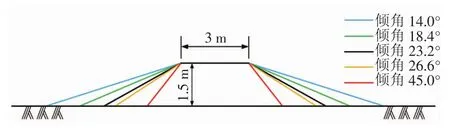
图2 砂袋堆叠不同倾角模型示意

通过模拟计算砂袋堆叠前后压力，得到压力差随水平高度分布情况（见图3），并且得到在不同砂袋堆叠倾角情况下，其周围流场压力云图和速度云图随砂袋堆叠倾角的变化情况（分别见图4和图5）。当砂袋堆叠倾角小于23.2°时，压力差随水平高度增加而增加，压力和速度变化幅度小，砂袋堆叠后方流场较为稳定，且倾角越大砂袋堆叠前后压力差就越大；当砂袋堆叠倾角大于23.2°时，压力差随水平高度增加呈现下降趋势，砂袋堆叠后方会形成漩涡，倾角越大漩涡的直径越大，压力差越大，而速度流场会发生扰动，且倾角越大扰动程度越大，增加流场不稳定因素。为避免来流在砂袋堆叠后方形成漩涡，进而对海床形成二次冲刷，砂袋堆叠倾角应该小于26.6°。

图3 砂袋堆叠前后压力差随水平高度分布

图4 不同倾角下砂袋堆叠流场压力云图/Pa

图5 不同倾角下砂袋堆叠流场速度云图/（m·s-1）

3.2 砂袋堆叠顶宽对流场的影响

取砂袋堆叠倾角18.4°，堆叠高度1.5 m，且保持倾角、高度皆不变，顶宽分别为2、3、4、5、6m，其底宽相应变化，依次为11、12、13、14、15m，模拟计算不同堆叠顶宽时（见图6）砂袋堆叠周围流场分布变化，分析堆叠顶宽对流场的影响。

图6 砂袋堆叠不同顶宽模型示意

模拟结果显示，不同堆叠顶宽的压力和速度云图趋势相同，且数值变化不大（见图7），砂袋堆叠前后压力差先随着水平高度增大而增大，当接近顶端时由于流体受到阻碍少，压力差随水平高度增加而减小。最大砂袋堆叠前后压力差出现在来流面靠近坡顶处，其所处高度约为砂袋堆叠高度的90%，随顶端宽度增加而减小，最小压力差出现在底端，随着顶端宽度增加而增加。当顶宽大于3 m时，平均压力差随顶端宽度增加而下降，但压力差下降很小，即顶端宽度对压力差影响较小；当顶宽小于3 m时，由于水流受到的砂袋堆叠阻挡作用变小，顶层砂袋受到的压力差大幅度增加。

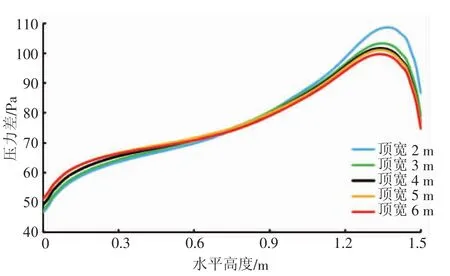
图7 砂袋堆叠前后压力差随水平高度的变化曲线

3.3 砂袋堆叠高度对流场的影响

取砂袋堆叠顶宽为3 m，堆叠倾角18.4°，且保持顶宽、倾角皆不变，堆叠高度分别为1.00、1.25、1.50、1.75、2.00 m，建立如图8所示的不同砂袋堆叠高度模型（其底宽相应变化，依次为9、10.5、12、13.5、15 m），模拟计算不同堆叠高度时砂袋堆叠周围流场分布变化，分析砂袋堆叠高度对流场的影响。

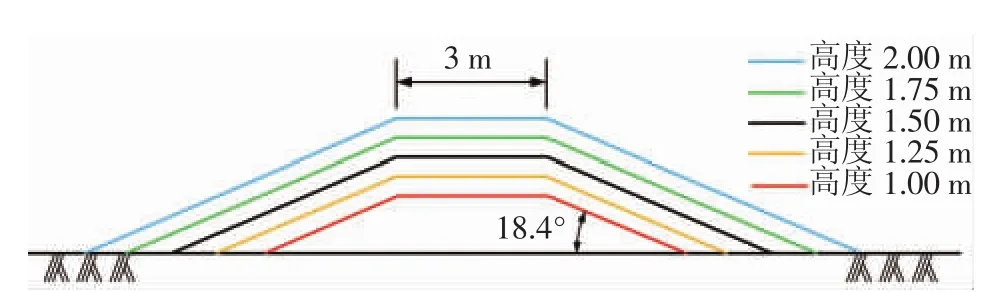
图8 砂袋堆叠不同高度模型示意

模拟结果显示，砂袋堆叠周围压力和速度变化趋势相同，但数值相差较大。砂袋堆叠前后压力差随水平高度变化曲线见图9，砂袋堆叠前后平均压力差会随着堆叠高度而增长，砂袋堆叠高度会大幅度地增加压力差。与原模型堆叠高度1.5 m时的平均压力差77.58 Pa相比较，堆叠高度1 m时平均压力差为64.51 Pa，下降了16.8%；堆叠高度2 m时平均压力差为93.85 Pa，上升了21.0%：堆叠高度越高，压力差增长越快。

图9 砂袋堆叠前后压力差随水平高度的变化曲线

4 结论及建议

（1） 当砂袋堆叠倾角小于23.2°时，砂袋堆叠前后压力差随水平高度增加而增加，压力和速度变化幅度小，砂袋堆叠后方流场较为稳定；当堆叠倾角大于23.2°时，压力差随水平高度增加而降低，而砂袋堆叠后方会形成漩涡，压力漩涡的直径随倾角增大而增大。为避免砂袋堆叠周围形成二次冲刷，砂袋堆叠倾角应小于26.6°。总体而言，压力差随堆叠倾角减小而减小，降低堆叠倾角可以降低被冲走的风险，但会增加用砂量。

（2）砂袋堆叠堤坝顶宽大于3 m时，顶宽对砂袋堆叠前后压力差影响较小，顶宽小于3 m时，由于水流受到砂袋堆叠的阻挡作用变小，顶层砂袋受到的压力差大幅度增加。减小堆叠顶端宽度可以减少用砂量，但顶宽过窄会使得压力差急剧上升，可能导致顶层砂袋被冲走甚至发生倒塌。

（3）砂袋堆叠高度增加会大幅度地增加压力差，且堆叠高度越高，压力差增加速度越快。在保证完全掩埋海底管道的基础上，降低砂袋堆叠高度，可以减少砂袋被冲走的风险，且能够减少工程施工成本。