充分发挥习题的“物理营养”帮学生跳出“题海”——谈谈变力的功的总复习

杨雄生 李春光

(北京中医学院附属中学 北京 100013)

张京文

(北京市朝阳区中学教研室 北京 100028)

面对高三总复习，许多教师采用“题海”战术，来帮助学生提高高考的成绩．大家也知道，这种总复习方法，师、生都很辛苦，教学效益还不高！

如何帮助学生跳出“题海”，提高复习效益？是一个大家都在探讨的问题．

我们主张，在高三总复习中，仍然要用实验来激发学生的学习兴趣，充分发挥实验和习题的“物理营养”，渗透物理思想与物理方法的教育，帮助学生跳出“题海”．

现就“变力的功”这个课题，介绍笔者的想法和做法，请同行批评、指正．

1 引入课题

上课伊始，先播放一段蹦极视频，让学生说视频反映什么事情？再说关于蹦极有许许多多的习题，我们这里就有一道题．

【例题】质量为75 kg的某人做蹦极运动，将一根长20 m弹性绳的上端绑在铁桥的钢梁上，下端绑在踝关节处，由于桥高有40 m之多，他从桥上跃下，最高点与最低点的高度差为30 m．为讨论方便，忽略空气阻力和其他的能量损失，并将“蹦极”者作为质点讨论，还忽略“蹦极”过程中偏离竖直方向的情况，g取10 m/s2．

问：在整个下落过程中，人克服弹性绳做了多少功？

师：关于蹦极可以编出各种各样的习题，不论是哪种题，都必须详细了解蹦极过程的物理过程的细节．为了解蹦极过程的物理细节，先来做个模拟实验：用钩码模拟蹦极者，橡皮筋模拟弹力绳，橡皮筋的上端系在铁架台的铁棍上，让钩码从橡皮筋的上端自由下落．(演示实验)大家看到了什么现象？

生：钩码在上下振动．

师：钩码为什么会这样运动？这个运动有4个关键的点，一个是最高点；一个是最低点；还有哪两个关键的点？

生甲：一个是自由落体结束，弹力开始起作用的点，还有一个点是重力和弹力平衡的点．

师：很好！这4个点将钩码运动分成3个阶段，请哪位同学给大家讲一讲钩码运动的情况？

生乙：(随着学生的讲述，教师画出图1中物体受力情况，提示并添上图中的a，b，e，c各点．)开始下落，钩码只有重力的作用，做自由落体运动，加速度为g；

图1

过了b点，橡皮筋开始伸长，钩码受有重力与弹力的作用，虽然，弹力一直在增大，但弹力小于重力，钩码向下做加速度减小的加速运动；

到了e点，弹力等于重力，这时钩码加速度为零，速度却达到最大值；

过了e点，弹力大于重力，而且弹力一直增大，重力不变，钩码所受到的合力一直在增大，但方向与速度方向相反，所以钩码做加速度增大的减速运动，到c点速度减到零，这就是最低点．虽然，钩码速度为零，但，所受的合力向上，它要继续往回运动．

师：好！这只讲了一半的运动，再请一位同学，讲一讲钩码由最低点c开始，运动到最高点a的情况．

生丙：钩码由c到e的过程，弹力一直减少，重力不变，但弹力大于重力，钩码所受到的合力一直在减少，钩码由静止开始，做加速度减少的加速运动；

到了e点，弹力等于重力，这时钩码加速度为零，速度达到最大值；

过了e点，弹力小于重力,且弹力一直在减少，钩码受到的合力一直在增加，但，合力的方向与速度方向相反，钩码做加速度增大的减速运动，这种运动只维持到b点；

过了b点，橡皮筋的弹力消失，钩码只受重力的作用，且重力与速度方向相反，钩码做加速度为-g的竖直上抛运动，由于不计空气阻力，钩码运动到a点，速度正好为零，但仍有重力的作用，所以，钩码就会重复原来的运动．

师：讲得很好！由于不计空气阻力和其他的能量损失，钩码就会不停地重复上述的运动．请注意，钩码由a到b，由b到e，由e到c的过程，与钩码由c到e，由e到b，由b到a的过程正好完全相反．或者可以说，它们互为逆过程．

仔细理解上述过程，对于讨论蹦极运动的习题或类似蹦极的一切习题都是很有帮助的，这也是我们解题的理论基础．

师：从上述的讨论，我们知道蹦极运动中，弹力是一个变力．如何求这个变力所做的功呢？

生：应用动能定理.

(引出课题)变力的功—— 动能定理的应用

2 讲解课题及解题

2.1 动能定理

表述1：合外力在一个过程中对物体所做的功，等于物体在这个过程中动能的变化．

公式：W合外力=ΔEk=Ek-Ek0→

表述2：在一个过程中外力对物体所做功之和，等于物体在这个过程中动能的增加量．

公式：∑W外=ΔEk=Ek-Ek0→

单位：不论是功，还是动能，其单位都是焦耳，

1 J=1 N·m=1 kg·m2·s-2

师：动能定理有两种表述，这两种表述是等效的，但解题程序有所不同．第一种表述，是先求物体所受的合力，再求这个合力在过程中的功，最后写出动能定理；第二种表述，先求每个力在过程中所做的功，再求各个力所做的功的代数和，最后写出动能定理．

2.2 解题

第二种表述的解题程序，往往能给解题带来方便．以本题为例给予说明．

解：以“蹦极”者为研究对象，他受力情况如图2所示．

图2

从最高点到最低点abc全过程，运用动能定理，有

(1)

因为v0=vt=0，故有

W弹=mg(hab+hbc)=2.25×104J

2.3 总结与讨论

(1)解本例的关键有三:

首先，按规范化解题．其中，分析研究对象受力情况，是求出该过程中，每个力做功多少的基础；

其次，对于变力，无法将它的功写成Fxcosθ的形式，通常写作W弹；

第三，采用上述表述2的解题程序来解题，就可以将两个不同加速度的过程，当作一个过程来研究．这也是利用动能定理求功带来的简便．

(2)如果过程的初、末状态的动能都是零的过程，这时变力功的表达式最简单．高中物理这类题目相当多．即使某过程的初、末状态的动能不都是零，也可以重新划分过程，让它的初、末状态的动能都是零的过程，这样就能给解题带来简便．

(3)对照本例还能吸取哪些“物理营养”？

就着本例，还可以来深入讨论下面的一些问题；

1)蹦极者克服弹力所做的功“干什么”？

蹦极者克服弹力所做的功，转变为他与弹簧的弹性势能了，而且，我们还知道，克服弹力做了多少的功，弹性势能就增加多少，它们的数值相等．

2)能求本例弹性绳的劲度系数κ吗？

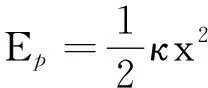
3)“蹦极”过程中，哪点的速度最大？请找到这点的位置并求出最大速度的大小？

重力与弹力平衡的那点，速度最大．

蹦极者受力情况如图1所示，对abe过程，根据动能定理，有

(2)

根据hbc=1.67 m,可先求出

将这两个数据代入(2)式，解得：vt3=20.4 m/s

4)“蹦极”过程中，加速度最大的点在那里？最大加速度多大？

最大加速度出现在最低点处，以竖直向下为正方向，由F合=ma可以求出其大小为

代入最低点的数据，有

请注意，如果上述方法求出的加速度的大小小于自由落体与竖直上抛的加速度大小10 m/s2，那么，最大加速度就应该是10 m/s2了．

5)仿照上述方法，可以求出“蹦极”过程中任何一点的速度与加速度！

大家知道，本例中，自由落体与竖直上抛运动中，位移随时间的变化图线是抛物线的一部分；弹性绳起作用时，蹦极者在竖直方向做简谐振动，它的位移随时间的变化图线是正弦或余弦曲线．

这样，就可以作出本例中蹦极者的位移随时间的图线，情况如图3所示．

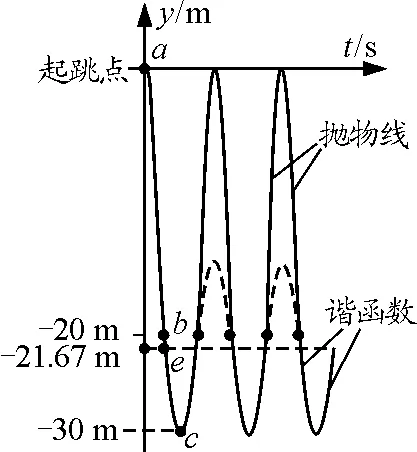
图3

2.4 拓展

师：北京2011年高考也有一道蹦极的单选题，分数6分．题目如下：

某人做蹦极运动，所受弹性绳子拉力F的大小随时间t变化的情况．如图4所示，将蹦极过程近似为在竖直方向的运动，重力加速度为g．据图可知，此人在蹦极过程中最大加速度约为

A．gB．2gC．3gD．4g

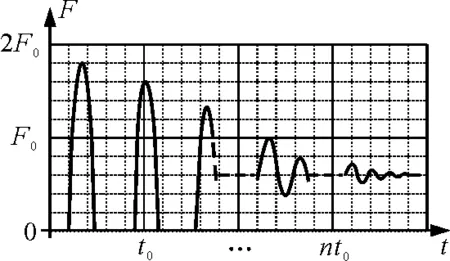
图4

师：有关蹦极过程，我们在上述例题中已经详细讨论了，不再重复了．

师：解本例题的关键是最大加速度应该出现在何处？

生：出现在弹力最大的最低点处．

图5

师：图4中有几个特殊点，如图5中a′,b′,c′,d′,e′,f′,g′,h′,i′各点，这些点表示什么意思？在什么“地方”出现？

生丁：a′,b′,c′,d′,e′,f′,g′点，出现在弹性绳刚刚被拉伸的时候，相当于图1和图3的b点．

生戊：a′,e′,i′点出现在弹力最大的最低点处，相当于图1和图3的c点．由于实际蹦极运动，都有能量损耗，弹性绳的最大伸长就会越来越短，所以，最大加速度应该出现在b′点处；

生己：i′点，表示蹦极振荡结束，蹦极者静止于弹性绳下的情况．

师：(板书)从图5中可知，对于i′点，有

mg=0.6F0

以mg为正方向，对于b′点，有

mg-1.8F0=ma最大

由以上两式，解得a最大=-2g，式中的负号，表示加速度的方向与mg方向相反．

故本题答案为B选项.

3 总结

3.1 作业

对于本堂课的作业：强调同学通过讨论，必须先弄清楚本堂课所讨论的内容的各个细节，才能去完成下面两道习题．

(1)质量为60 kg的运动员，从10 m台跃起，其最高点高出跳台1 m,入水后潜入2.5 m, 才返回．为讨论方便，忽略空气阻力，并将运动员作为质点讨论，还忽略跳水过程中偏离竖直方向的情况，g取10 m/s2．

问：运动员克服水的作用力所做的功？运动员克服水的作用力所做的功，“干什么”？

(2)2011年全国新课标卷，第16题，分数6分，也是一道有关蹦极的选择题，题目略．要求解选择题时，必须通过讨论说明选择这个选项的理由；不选那个选项的理由．

3.2 几点说明

(1)本课播放蹦极视频、做模拟实验，都是为了激发学生学习物理的积极性，也是为理论分析打下情感基础．我们主张尽量活跃总复习课的课堂气氛，学生喜欢物理了，教学效益自然会提高；若把总复习课“搞得”死气沉沉，枯燥无味，教学效益很难提高．

(2)讨论图1所示的蹦极者受力、加速度以及运动情况，是解这类题的理论基础．为了促使学生思维，提高悟性，对于一般程度的学生，不宜由教师自己讲授，应该舍得花时间，通过师、生讨论得出，才能让学生印象深刻，为真正理解习题物理过程的细节打下扎实的基础．

同时要求，课后必须通过讨论，先“搞懂”课堂上所讨论的内容细节，而后才能去完成作业．长期渗透这种方法，让学生养成这样的学习习惯，才能提高学习效率．

所谓充分发挥习题的“物理营养”，主要是让一般程度的学生，真正理解题目涉及到的物理过程的细节，在此基础上，学会思考问题与解题表述方法．这样才能真正起到“举一反三”的作用，才能帮助学生跳出“题海”．

(3)关于图3的位移随时间的变化图线，对于一般程度的学生，真正理解起来有难度，是作为可有可无的“零级教学目标”出现的，如果有学生暂时理解不了，也不会影响“后续”的学习，不作为必须完成的教学目标．

2011年的11月14日，本课在北京市朝阳区作为研究课展示，课后评议时，教师们对于这样充分发挥习题“物理营养”的做法，大多表示认同与肯定；但是，也对高考总复习中出现考试不要求的弹性势能的表达式有不同意见．

对这个问题笔者这样认为，人民教育出版社高中教材《物理·必修2》第七章第5节“探究弹性势能的表达式”，当时要求着重体会探究的过程与所用的方法，不要求掌握结论，更不要求用结论解题．到了高考总复习，增加弹性势能的表达式，能够加深对弹力做功的理解，也能够加深对机械能的理解，对学生学习物理有好处，并不增加学生太多的负担．

北京中医学院附中的学生程度，在朝阳区属于中等偏下的，这堂课后对学生进行调查，学生对出现弹性势能的表达式(教师以前讲过)，并不感到突然，对于弹力的功和弹性势能的关系，也不感到难于接受，对于这样的复习课表示欢迎．

以上内容是我们对高中总复习课的想法与做法，仅为一家之言，提出来与大家讨论，敬请同行批评指正．