螺绕环的电感

任保文

(西安电子科技大学物理系 陕西 西安 710071)

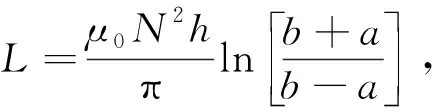
下面给出几种常见情况的准确解．

1 椭圆形截面螺绕环的自感计算

如图1所示,设细线密绕螺绕环的椭圆截面半轴长为a,h,环心到椭圆中心的距离为b,总匝数N.细线导线电流为I,甚至电流无角向分布.由安培环路定理得,螺绕环内的磁感应强度为

图1 螺绕环

设环面方程为

切点为

椭圆截面上的磁通量为

Φ的表达式中r1,r2是方程(h2cos2θ+a2sin2θ)r2-2brh2cosθ+h2b2-a2h2=0的两个根．有

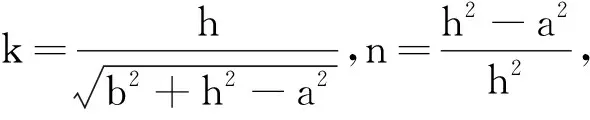
其中

而

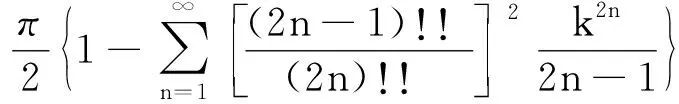
故有

则自感为

其近似表达式为

对于圆形截面螺绕环,有a=h,n=0其自感为

若a=5 cm,b=15 cm,N=1 000.其理论值为

L理=1.062 39×10-2H

近似值为

L近≈1.062 35×10-2H

由数值计算可知,理论值与近似值的误差甚微,可以忽略.

由能量法有

也可求得自感L，以下计算略.

2 矩形截面螺绕环的自感计算

如图2所示，设螺绕环截面为矩形,长宽分别为2a,2h．

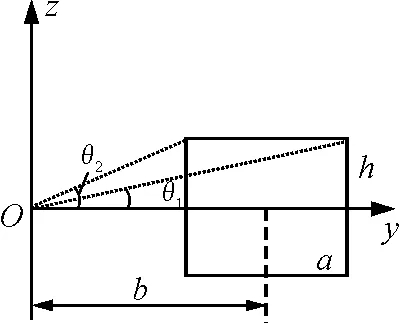
图2 矩形螺绕环截面

同理得磁通量

式中b-a=r1cosθ,b+a=r2cosθ,h=r3sinθ;

得

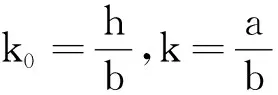
故螺绕环的自感为

可得近似式

若螺绕环截面为正方形(k=k0),可得近似式

直接用近似法有

若a=5 cm,b=15 cm,h=4 cm,N=1 000.得自感的理论值、近似值和直接近似值分别为

L理=1.093 7×10-2H

L近=1.093 6×10-2H

L直近=1.110 6×10-2H

由数值计算可知,理论值与近似值误差甚微.直接近似误差接近2%,一般需要修正，由上面可以看出，大学物理教课书中的近似方法直到k的一阶项是正确的，由此亦可判定理论结果的正确性程度，求积分时亦可用数值积分来处理．由于螺绕环在磁介质研究中的常用性,因此，该结果不管在理论上还是实践中都有一定的借鉴意义.

参考文献

1 赵凯华,罗蔚茵．电磁学．北京：高等教育出版社，2006.12

2 赵凯华,罗蔚茵，陈熙谋．新概念物理题解．北京：高等教育出版社,2006.6

3 任保文,郑亚娥. 单自由度非线性保守系统作大振幅振动时周期的计算方法.大学物理，2005,24 (3):15～17