论纯电阻电路的电源输出功率与电阻的关系——解读电源输出功率随电阻变化的曲线

冷芬全

(江西省修水县第一中学 江西 九江 332400)

1 问题提出

【例1】如图1所示，电源电动势E=4 V，内阻r=4 Ω，R′为滑动变阻器，其电阻的最大值为3 Ω,则电源的最大输出功率是多少.

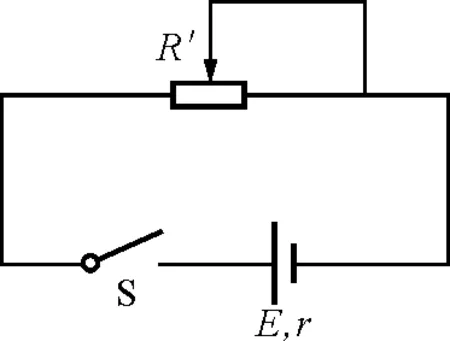
图1

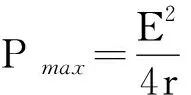
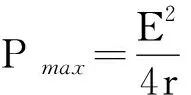
2 理论依据

在“恒定电流”的闭合电路的欧姆定律一节中，对于纯电阻电路来说，电源的输出功率

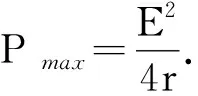
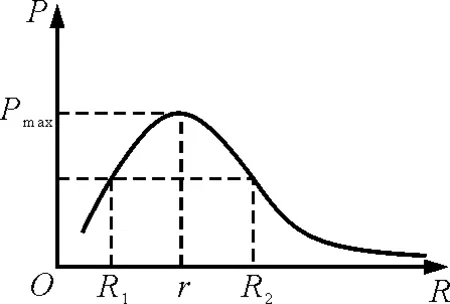
图2 电源输出功率随外电路电阻变化的曲线

【例2】如图3所示，电源电动势E=6 V，内阻r=3 Ω，定值电阻R0=0.5 Ω，R′为滑动变阻器，其电值的最大值为10 Ω,则电源的最大输出功率和最小输出功率分别为多少.

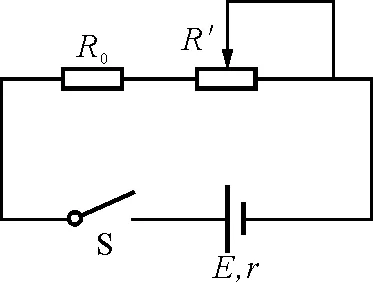
图3

解答：外电路电阻Rx与电源内阻r相等(R′=2.5 Ω)时，电源的最大输出功率

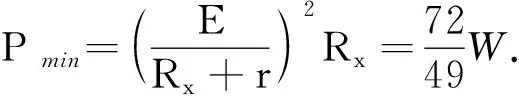
如果例2题中定值电阻R0=2 Ω，由R1R2=r2可知Rx=(R0+R′)= (2+10) Ω=12 Ω时电源输出功率最小

分析：

电源的最小输出功率由R1R2=r2和图2进行比较(如果外电路电阻等于零时，输出功率最小为零，但因电源要求而不允许)．

(2)外电路电阻Rx的最大值小于电源内阻r．当外电路电阻Rx不断增大的过程中，由图2可知电源的输出功率P一直增大，并且当外电路电阻Rx最大时，电源的输出功率P最大．当外电路电阻Rx最小时，电源的输出功率P最小．上述例1就属于这种情况．

(3)外电路电阻Rx的最小值大于内电阻r．随外电路电阻Rx从零不断增大的过程中，由图2可知电源的输出功率P一直减小，并且当外电路电阻Rx最小时，电源的输出功率P最大．当外电路电阻Rx最大时，电源的输出功率P最小．

3 问题拓展

3.1 闭合电路中某个定值电阻消耗的功率

【例3】如图4所示，电源电动势E=4 V，内阻r=4 Ω，定值电阻R0=6 Ω，R′为滑动变阻器，阻值范围为(0～10 Ω),则定值电阻R0所能消耗的最大功率与最小功率分别是多少.

图4

3.2 闭合电路中可变电阻消耗的功率

此类情况通常采用等效电源法，将用电器获得的功率转化为电源的输出功率来进行处理，我们可以把定值电阻等效为电源内阻，即电源内阻就相当于(R0+r),滑动变阻器R′就成了外部电路电阻了，同样可以参照电源输出功率随电阻变化的曲线进行解答．

【例4】如图5所示，电源电动势E=6 V，内阻r=3 Ω，定值电阻R0=10 Ω，R′为滑动变阻器，其电阻的最大值为20 Ω,则滑动变阻器阻R′所消耗的最大功率Pmax是多少.

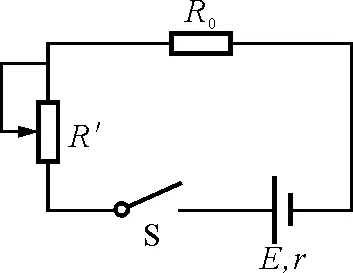
图5

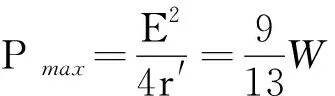
例4题中如果滑动变阻器电阻的最大值为10 Ω,

则当滑动变阻器的阻值最大时，所消耗的功率最大．

3.3 电源的功率

电源的功率，电源内阻一般认为是定值，由P=UI=EI可知，只要电路中的电流I最大(或最小)，即电路中的总电阻最小(或最大)，则电源的功率就最大(或最小)．

【例5】如图6所示，电路中电动势E=5 V，r=10 Ω的电源，R0=90 Ω的定值电阻与最大值400 Ω的滑动变阻器R′；在调节R′过程中，求电源的最大功率与最小功率.

图6

解答：当电路中的总电阻最小时，电流最大，则电源的最大功率

当电路中的总电阻最大时，电流最小，则电源最小功率