例谈“等效法”在高中物理解题中的应用

龚建成

(石庄高级中学 江苏 南通 226531)

等效法是物理学中常用的一种研究方法，尤其在高中物理教学中应用得更为广泛．例如：在研究力的合成与分解时，合力与分力就是等效替代关系；研究平抛运动时，常把它等效成水平方向的匀速直线运动和竖直方向的自由落体运动；研究交流电时常用到电流、电压的有效值等．

等效法是把复杂的物理现象、物理过程转化为简单的物理现象、物理过程来研究和处理的一种科学思想方法，它也是物理学研究的一种重要方法．若能将此方法渗透到高中物理解题的分析中，不仅可以使问题的分析和解答变得简捷，而且对知识的灵活运用、能力的提升都会有很大的帮助．下面通过几个实例来谈谈等效法的具体应用．

1 等效法在复合场中的应用

【例1】如图1所示，在沿水平方向的匀强电场中有一固定点O，用一根长度为l=0.40 m的绝缘细线把质量为m=0.20 kg，带有正电荷的金属小球悬挂在O点，小球静止在B点时细线与竖直方向的夹角为θ=37°.现将小球拉至位置A使细线水平后由静止释放，求：

(1)小球运动通过最低点C时的速度大小；

(2)小球通过最低点C时细线对小球的拉力大小；

(3)如果要使小球能绕O点做圆周运动，则在A点时沿垂直于OA方向上施加给小球的初速度的大小应满足什么条件．

(g取10 m/s2,sin37°=0.60 , cos37°=0.80)

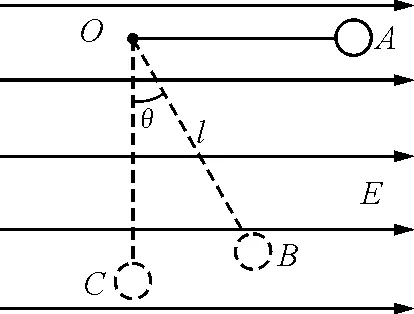
图1

解析：本题的第(3)问中求在A点施加给小球的初速度应满足什么条件才能使小球绕O点做圆周运动，关键是要找到小球在电场和重力场组成的复合场中的等效最高点．具体做法是把小球受到的重力与电场力的合力等效成重力G′，这样就跟在重力场中的处理方法一样，使问题简单多了．

(1)小球受到电场力qE，重力mg和绳的拉力作用，处于静止，根据共点力平衡条件有

对于小球从A点运动到C点的过程，根据动能定理有

解得小球通过C点的速度

(2)设小球在最低点时细线对小球的拉力为T，根据牛顿第二定律有

解得

T=3 N

(3)因为小球在运动过程中所受的重力与电场力始终保持不变，故可以将它们的合力视为等效重力G′，则

等效重力的方向与竖直方向所成的夹角α满足

所以小球作圆周运动过程中的等效最高点为BO的延长线上的B′，且与B关于O点对称，如图2所示.设小球在等效最高点B′的最小速度为v，由

得

小球从A到B′的过程中由动能定理得

图2

点评：用等效场力或等效重力加速度是处理带电粒子在复合场中运动的一种常见方式，一般是将重力和电场力的合力作为等效重力，从而求出等效重力加速度的大小和方向，其他解法与重力场中物体的运动规律相同．

2 等效法在电磁感应中的应用

(1)推导出感应电动势e的大小与金属棒的位移x的关系式;

(2)整个过程中力F所做的功;

(3)从A到导轨中央的过程中通过R1的电荷量．

图3

解析：本题是一道较为复杂的电磁感应题，在推导出感应电动势e的表达式后，就会发现电路中产生的是交流电．然后把要求的第(2)、(3)问中的问题等效成线圈转动时产生的交流电来处理，问题就容易多了．

(1)金属棒MN与两条金属导线相接触的长度

因两条金属导线形状为正弦曲线，所以，感应电动势为交变的，有

(2)因为x=vt，所以

由于导体做匀速运动，力F所做的功等于电路中电流所做的功．有效值

导体切割磁感线的时间

电路中总电阻

拉力F所做的功

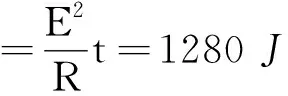
Emax=BSω=Φmω

所以

通过电阻R1的电量为

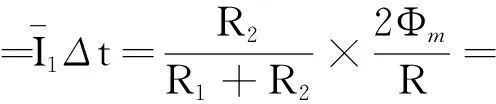
点评：本题从产生的结果上看，金属棒运动产生的交流电与线圈转动类似，因此从这一角度去分析、处理，可以达到化难为易的目的．

3 等效法在恒定电流中的应用

【例3】在图4混联电路中，电源的电动势ε=6 V，内阻r=1 Ω，R1=5 Ω，R3=4 Ω，R2的阻值范围为0～10 Ω．问R2取何值其功率最大？最大功率多大？

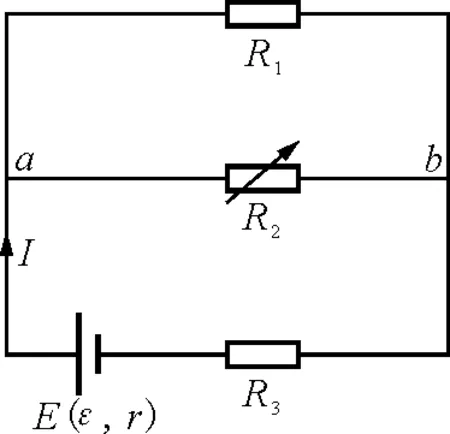
图4

解析:可以把R1，R3纳入E内，跟E构成等效电源E0(ε0，r0)，如图5中虚线框内电路所示．等效电动势ε0等于E0外电路断路时的路端电压Uab,即

ε0=Uab

图5

当R2=r0时，R2功率(即E0输出功率)最大

点评：这类题目通常把外电路中的全部定值电阻都纳入电源内，把它们当成电源内阻的一部分，这样电源就等效成一个新的电源，而外电路就剩下了可变电阻，从而使较复杂的直流电路问题变成简单的电路问题，可见，等效变换法不失为解决问题的一种有效方法．

4 结语

通过以上几例的分析和解答，可以看出合理恰当地运用等效法解题，能将许多物理问题化繁为简、化生为熟、化难为易，可谓事半功倍．作为物理教育工作者，更要在平时的教学中注意这一思想的渗透，这不仅有利于提高学生的解题速度，而且对学生灵活运用知识起到很大的帮助，同时还有助于学生创造能力的培养，可谓一举多得．