对饮料杯重心位置最小值的探讨
郑 金
(凌源市职教中心 辽宁 朝阳 122500)
文献[1]利用质心计算公式导出重心位置坐标跟水面高度的关系式,然后求导数得出重心位置的最小值,其解题过程和结果都是正确的,但在求极值时两次对分式求导数,难度较大,而且所得结果不是最终答案,还需进一步化简.那么除了原解以外,是否还有其他方法呢?现对上述问题进行探讨.
原题:如图1所示,一个饮料杯装满水,杯的底部有一小孔,在水从小孔不断流出的过程中,杯连同杯中水的共同重心将
A.一直下降 B.一直上升
C.先升后降 D.先降后升

图2

图1
原解:建立空间直角坐标系如图2所示,假设饮料杯的质量为m,高度为h,杯底的半径为r,水的密度为ρ,当水面到杯底的高度为l时,水的质量为M=ρπr2l由质心公式得整体重心的位置为

用求导数的方法得出的重心位置的最小值为

这个结果显得非常复杂,其实还可化简为

下面再给出两种简单解法.
解法1:质心坐标法
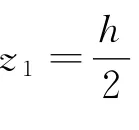

可知,整体重心的位置为
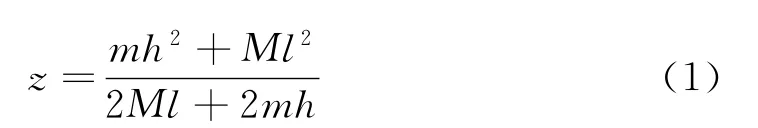
把M=ρπr2h代入得

可利用判别式求极值,需把函数关系式变形为关于l的一元二次方程的形式,由(1)式得
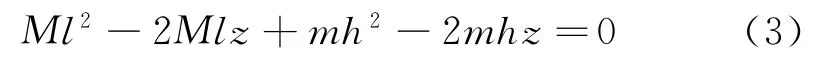
因重心最低的位置只有一个,则对应的l值只有一个,即方程有唯一解,只有一个根(两个相同的根),其条件是判别式为零,即

化简得

考虑到重心高度z大于零,解方程(5)得

此时l有唯一值,对方程(3)由极值条件得

所以,当整体的重心最低时,水面与重心位置等高.
解法2:势能叠加法
对于变质量物体,若在其重心的左侧增加质量,则重心位置将向左移;若在其重心的右侧增加质量,则重心位置将向右移.同理,若在其重心的左侧减少质量,则重心位置将向右移;若在其重心的右侧减少质量,则重心位置将向左移.
当满杯水时,重心在几何中心,位于水面以下.当开始放水时,是在整体重心上方减少质量,则重心将下移,同时水面也下降,但由于杯的重心固定不动,则整体重心下降的速度比水面下降的速度慢,当水面下降到与整体重心重合时,若继续放水,则是在整体重心下方减少质量,那么整体重心将上升,由此可见,整体重心的位置是先降后升,因此整体重心的高度存在最小值,即当水面与整体重心的位置重合时,整体重心的位置最低.
以杯底为重力势能的零势能面,当整体的重心最低时,重心位于水面上,设此时杯中水的高度为l,则水的质量为

其重力势能为

杯的重力势能为

整体重心到杯底的高度也为l,则整体的重力势能为

根据整体的重力势能等于各部分的重力势能之和有

代入并整理得

解得

所以整体重心位置的最小值即水面的高度为

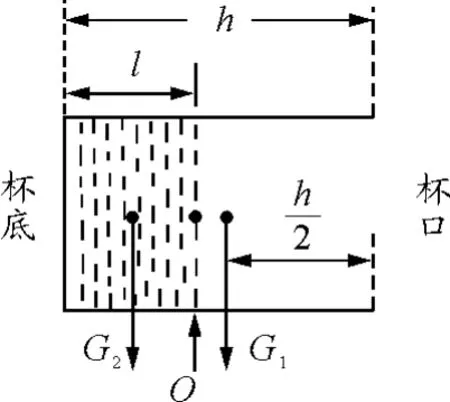
图3
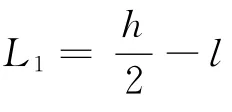
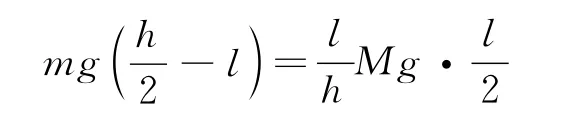
整理得
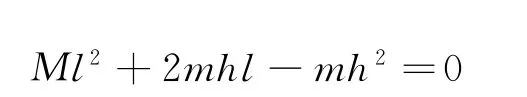
由此可解得整体重心位置到杯底距离的最小值.
1 宫长莹,石安山.探究饮料杯重心的变化规律.物理通报,2011(3):70~71

