不同基体平面压痕应力强度因子
蔡永梅, 王 伟, 谢禹钧
(1.中国石油大学(华东)储运与建筑工程学院,山东青岛266555;2.辽宁石油化工大学机械工程学院,辽宁抚顺113001)
接触问题会引起局部的应力集中,当物体的几何条件、物理参数满足一定条件时会产生局部急剧的应力变化梯度,甚至奇异应力场。与裂纹情形类似,当载荷达到临界值时,在应力奇异环处开裂,形成一个圆环形的浅(微)裂纹。尤其是刚性压头冲压弹性半平面基体时,在两个角点处产生奇异应力场。这类应力场不仅会导致材料的开裂和失效,也会引起触压边界的开裂[1]。在这两种情况下,应力强度因子均表现为断裂参数,也是奇异应力场的唯一控制参量。该断裂参量是导致工程部件失效的主要因素[2-4]。本文将基于文献[5]提出利用无裂纹接触问题生成I型奇异应力场的原理进行数值分析。
1 接触问题和守恒律
压头的几何形状如图1(a)所示。假设接触表面足够光滑,使接触面没有因摩擦产生的剪应力。刚性方形压头宽为2l,作用载荷P,压在无摩擦的半平面上,泊松比为μ。文献[6]经典分析给出的接触压力分布如下:

改变坐标x1=r-l,应用二项分布扩展方程,当r非常小时,得到压头尖角附近的压力变化

这些应力分量和图1(b)所示的x2=0时I型裂纹产生的应力分量的表达式一样,实际上,沿线x2=0的边界条件等同于接触裂纹问题,这两个问题内部应力状态的奇异性相同,文献[5]给出其应力分布如下:

(3)式中延用了裂纹问题的应力强度因子习惯表示方法,但为压应力场。其中KI定义为基体近表面压头角点处的奇异应力场的应力强度因子,或压痕边缘处奇异应力场的应力强度因子,表示为:

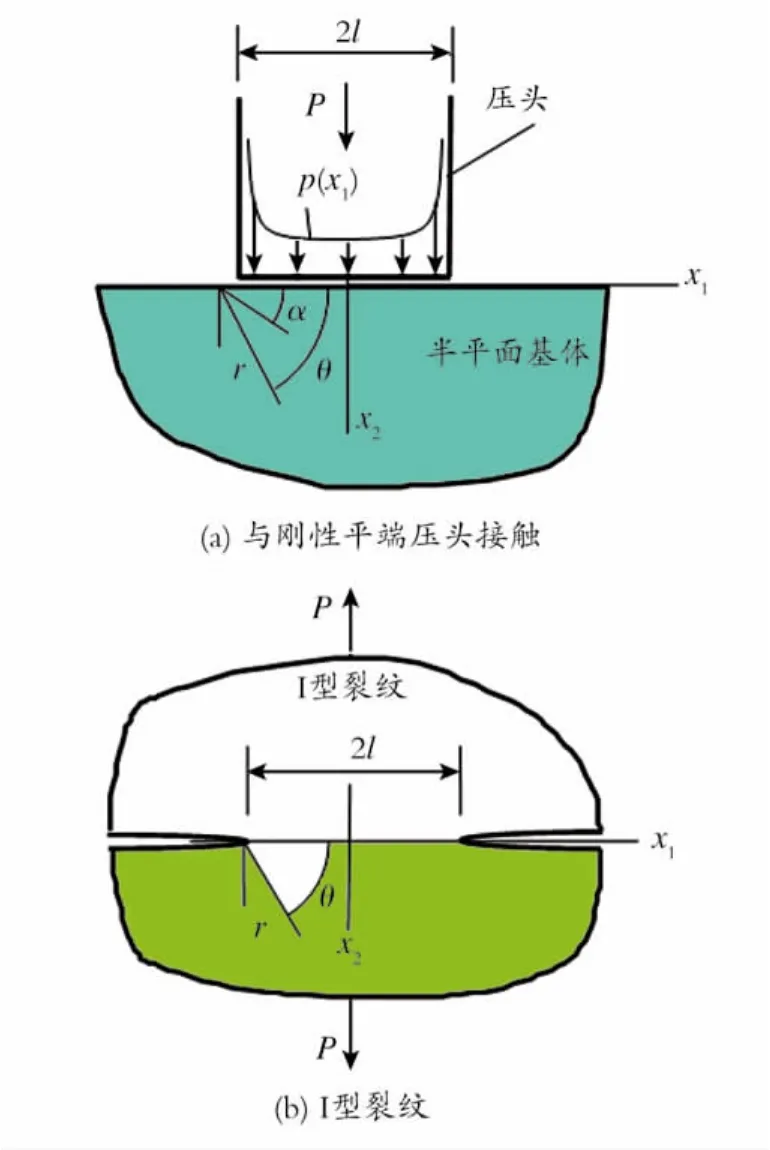
Fig.1 A schematic representation of the contact between a two-dimensional rectangular punch and a substrate图1 二维矩形压头和基体的接触
如果方程(3)中的负号改为正号,这个结果和在远场承受载荷P时的无限平板裂纹(裂纹韧带长度为2l)的情形一样。与裂纹问题类似,表明压头拐角附近存在I型奇异应力场和K-控制区。如方程(3)所示,应力强度因子KI是唯一控制应力场的参数,这意味着,沿着接触表面的边界裂纹和I型裂纹有着同样的破坏机理。实际工程结构中可利用奇异应力场,研究材料的破坏行为、测试材料的机械性能。
对于二维弹性体,文献[7]由守恒定律得出下面的积分

方程(5)有两个分量J1和J2。其中w是应变能密度;nj是外法线矢量;Ti是沿积分路径的应力矢量;ui,j位移分量。对于没有裂纹和空穴的封闭积分路径,Ji为0。J1称为J-积分和J2称为G*-积分[8]。它们都可用于计算弹性体裂纹的应力强度因子[9-10]。下面给出J1积分在刚性压头冲压弹性平面情况下计算应力强度因子中的应用。
2 冲压弹性半平面应力强度因子
平板承受压头冲压如图2所示。在每个压头的2个拐角处有I型奇异应力场。应力场由方程(3)来表述。取沿sc=sba+safe+sed+sdcb封闭路径积分,如图2所示,当sdcb在压头尖角处的K控制区内时,由文献[8]已得出如下结果。
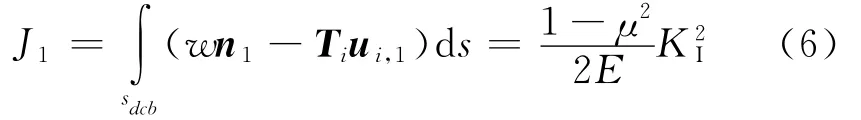
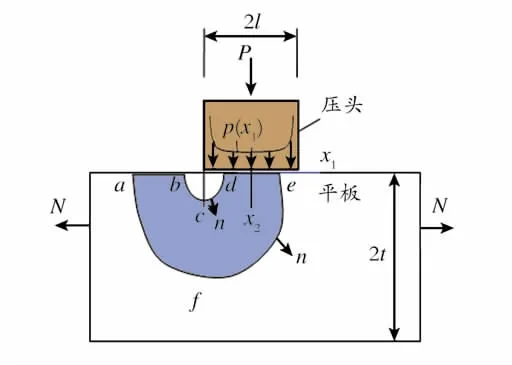
Fig.2 The panel under indentation and integration path图2 平板承受压头时的积分路径
按照Griffith’s理论[11],弹性固体产生新的断裂表面所需要的能量来自弹性体的能量释放外力所做的功。Griffith理论给出的临界载荷为最小的边界开裂载荷,开裂方向为最大能量释放率的方向。当压痕沿开裂的能量释放率达到临界值即开裂韧性Gc时,边界将开裂,即:
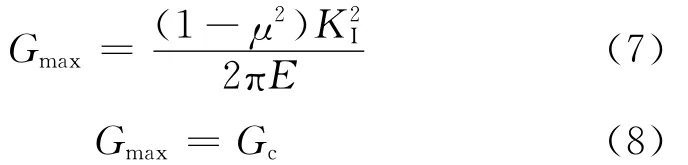
如果将压痕边界开裂所需的能量理解为与裂纹开裂的情形相同,即:
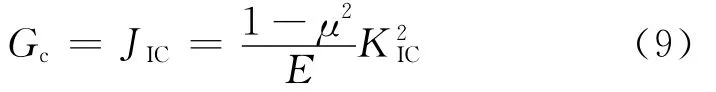
KIC为裂纹扩展的断裂韧性。触压临界开裂条件为:

由方程(6)得出应力强度因子可以利用J积分来计算,对于不同的材料可以得出不同的KIC。工程中许多材料遇到断裂问题,因此本文选用一些常用材料的弹性模量和泊松比分析K值变化。
3 数值分析
基于守恒律及方程(6),应用有限单元法进行数值计算,数值分析计算中采用了有限元分析系统ANSYS13.0,有限元模型选用平面应变单元。平板基体材料泊松比μ,弹性模量E(MPa)如表1所示,刚性压头宽度2l,l=10mm;平板宽度为40l,高度随着l/t的取值而变化。压头与平板触压形成奇异点处的网格如图3所示,接触边缘采用四分点单元。边界条件:平板底端,uy=0,在刚性压头控制点施加载荷P=10 000MPa;基于表1,针对不同弹性模量、泊松比和不同的l/t值进行多组数据求解,结果如表2和图4-6所示。

表1 不同材质弹性模量及泊松比Table 1 Different elastic modulus and poisson ratio

表2 不同材质应力强度因子Table 2 Stress intensity factors in different material

Fig.3 The mesh of singular point(l/t=0.2)图3 奇异点网格(l/t=0.2)


Fig.4 Stress and contact pressure(l/t=0.2)图4 应力和接触压力(l/t=0.2)

Fig.5 Elastic panel is subject to indentations图5 平端圆柱压头冲压半平面压痕
图4(a),(b)分别描述当l/t=0.2时,应用有限元软件计算出模型的应力和接触压力分布,图5给出圆柱形刚性平端压头冲压半平面实验结果,比较图4和图5,很显然在压头角点处会产生的奇异应力场,且该应力场将引起微裂纹。图6绘制出基于数值计算得出KⅠ,P和l/t的关系。随着l/t的增加,正则化的应力强度因子和断裂韧性逐渐减小,表明了边界对应力强度因子的影响;随着材质弹性模量减少,正则化的应力强度因子逐渐减小,表明了材料弹性模量及泊松比对应力强度因子的影响。
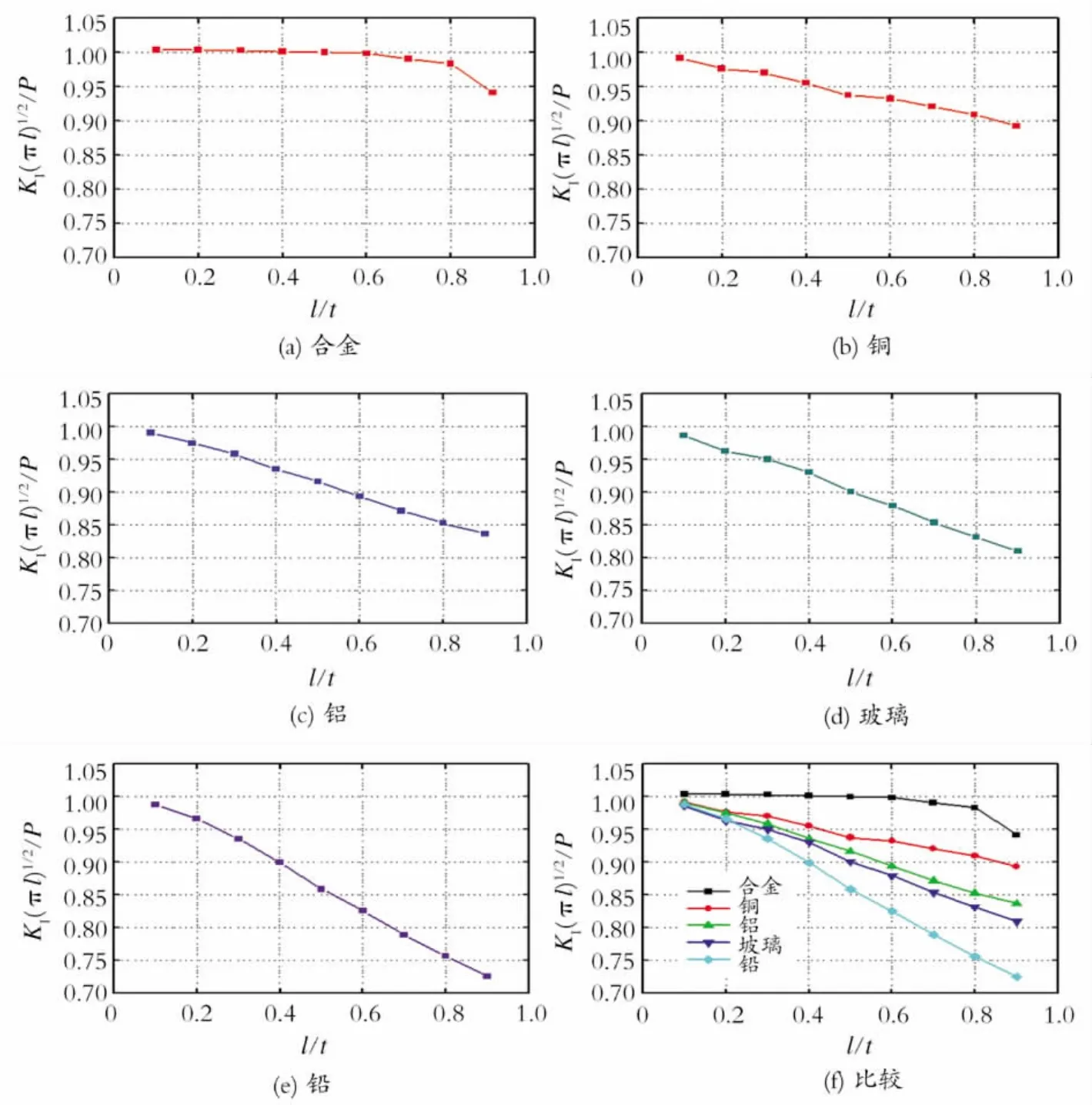
Fig.6 Normalized fracture toughness for different ratio of l/t图6 不同l/t下的正则化应力强度因子
[1] Xie Y J,Hills D A.Crack initiation at contact surface[J].Theoretical and applied fracture mechanics,2003,40(3):279-283.
[2] Xie Y J,Hills D A.Quasibrittle fracture beneath a flat bearing surface[J].Engineering fracture mechanics,2008,75(5):1223-1230.
[3] Porter M I,Hills D A.Adhesive contact between a rigid punch and a half-plane via a thinsoft interlayer[J].J.eng.mech.,2001,127:176-179.
[4] Hills D A,Porter M I.A flat punch pressed against an elastic interlayer under conditions of slip and separation[J].Int.j.mech.sci.,2002,44:465-474.
[5] Nadai A I.Theory of flow and fracture of solids[M].New York:McGraw-Hill,1963.
[6] Johnson K L.Contact mechanics[M].Cambridge:Cambridge university press,1985.
[7] Sih G C.Dynamic aspects of crack aspects of crack propagation[M]//Inelastic behavior of solids.New York:Mc-Grawhill book,Co.,1969:607-639.
[8] 王晓华,蔡永梅,谢禹钧.平板双侧触压的应力强度因子[J].工程力学,2009,26(3):30-32.
[9] 王伟,谢禹钧.I型类中央双裂纹椭圆形界面管环向裂纹应力强度因子[J].辽宁石油化工大学学报,2010,30(3):55-57.
[10] 王晓华,马英利,孙壮,等.周期阵列压痕奇异应力场与开裂[J].石油化工高等学校学报,2009,22(2):63-66.
[11] Griffith A A.The phenomena of rupture and flow in solids[J].Phil.trans.roy.soc.London,1921,A221:163-198.

