柱壳周期阵列平齿取芯钻断裂型破岩机理

王 莹， 龚 雪， 王晓华

（辽宁石油化工大学机械工程学院，辽宁抚顺113001）

天然岩石质地坚硬耐磨，是传统的建筑与装饰材料。原料石材到石材制品要历经切割、磨平和抛光的机械加工工序，其中切割所占份额最重。同时，探矿和采矿工程中的钻头钻取岩心、市政和土建工程中的混凝土锯切机具等等，均为非金属高硬脆性材料的代表性锯切行为。典型的平齿取芯钻如图1所示，钻头的锯齿由柱壳周期阵列平端金刚石压头（节块）组成。该类切割工具锯齿形状选择主要来自实践经验。传统的观点认为，该类钻具切割岩石的机理为金刚石磨料在金属结合剂的把持下对岩石材料的磨削［1］，但实际上，该传统观点仅仅说明了平齿类破岩工具切割行为的一个方面。本文的研究将从平面压痕断裂力学的角度，揭示压痕边界断裂型开裂对平齿切割工具破岩机理的贡献。

Fig.1 Typical rock drill with flat－tipped indenters图1 典型平齿取芯钻

1 平面压痕断裂力学模型

典型的二维平面压痕问题如图2所示。即当刚性矩形压头作用在半平面均质各向同性弹性体的边界上时，在弹性体的表面形成一个平面压痕。若压头的半宽度为a，摩擦系数为f，且基体为不可压缩弹性体或f＝0时，则在压痕的边界处，即压头角点处存在Nadai A I［2］给出的如下渐进奇异应力场：

其中［3－7］：

和

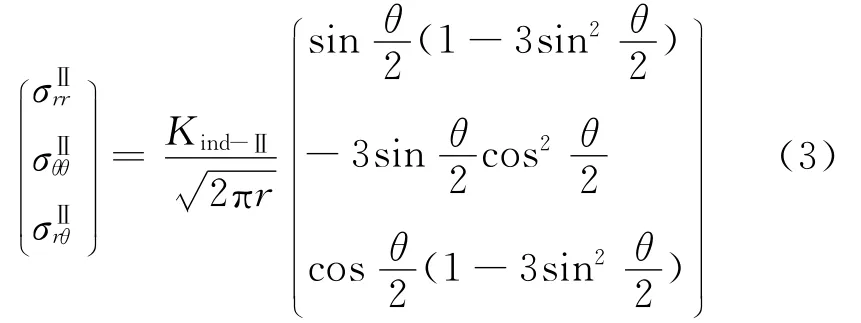
其中

由（2）式可以看出，其应力场的奇异性和分布与I－型裂纹的奇异应力场相同，为典型的I－型奇异压应力场。Kind－Ⅰ表现为I－型平面压痕的应力强度因子。同时应当注意到，（3）式为典型的II－型裂纹的奇异应力场，Kind－Ⅱ表现为II－型平面压痕的应力强度因子。两种奇异应力场强度均可由平面压痕应力强度因子描述。如同裂纹问题一样，在压头的角点处存在Kind－控制区。

Fig.2 Indentation configuration图2 平面压痕构型

上述分析表明，当矩形刚性压头作用在半平面弹性体的表面时，在平面压痕的边界处将诱生裂纹型渐进奇异应力场。表明矩形刚性压头可以用较小的载荷在基体表面诱生高度的应力集中，包括压头与弹性体之间的界面压力也具有奇异应力特征并在压头的角点处呈现高度的应力集中，不仅有利于磨料磨削基体的表面，更重要的是所诱生的奇异应力将导致压痕边界的断裂型开裂，如同裂纹尖端的开裂，对破岩行为有直接的贡献。

应当指出的是，当基体为有限边界问题时，（2），（3）式给出的奇异应力场仍存在，只是式中的Kind－Ⅰ应由具体的边界条件确定。

2 柱壳周期阵列平面压痕的应力强度因子

平面压痕应力强度因子是控制压痕边界开裂的重要断裂分析参量。载荷、摩擦系数以及钻头的几何参数等对岩石切割行为的定量贡献，均通过平面压痕应力强度因子和压痕边界开裂准则实现。因此，平齿类切割工具破岩机理研究中，平面压痕应力强度因子的分析计算是关键环节之一。

2.1 周期阵列柱壳平面压痕构型

在法向载荷P和扭转载荷M作用下的圆柱壳周期阵列刚性压头及圆柱壳基体如图3所示，可作为典型的取芯钻简化破岩模型。设周期阵列压头的数量为m（图3中m＝6），t为压头和基体壳的厚度，R为中径，且t／R足够小。于是依据渐进应力场分析理论，在每个柱面平端压头的尖角处存在由（2）和（3）式给出的应力场。

Fig.3 Configuration for the cylindrical periodic surface contact with mflat－tipped indenters（m＝6）图3 m个周期阵列柱壳平端刚性压头及基体构型

2.2 圆柱壳周期阵列压痕的应力强度因子

对于具有m个周期阵列压头的接触力学问题，存在2 m个奇异应力场。本节用裂纹当量方法给出圆柱壳周期阵列压痕的应力强度因子。

文献［7－8］指出，平面压痕边界的渐近应力场状态与裂纹问题等价，即图2所示的压痕边界的奇异应力场与图4（a）所示的裂尖奇异应力场相同，可以用等价裂纹体求解压痕的应力强度因子。由于拥有大量各类裂纹应力强度因子的解，采用当量法将给压痕问题应力强度因子的求解带来极大的方便。同样，本文讨论的圆柱壳周期阵列压痕问题如图3所示，等价于图4（b）所示的在相同载荷作用下圆柱壳周期裂纹问题。于是由文献［8］给出的方法可以得到I－型平面压痕应力强度因子［9］：

其中正则化的压痕应力强度因子为：

进而由（4）式可以得到II－型平面压痕应力强度因子为

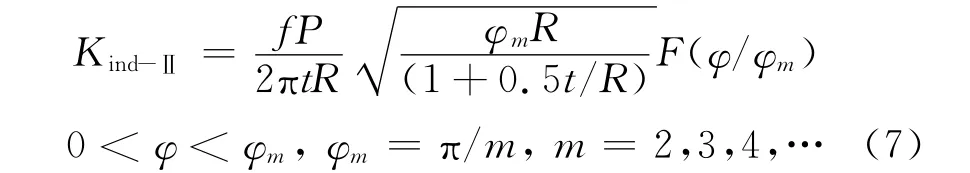
Fig.4 Equivalent crack configurations图4 当量裂纹构型

3 平齿取芯钻断裂型破岩的临界条件

当摩擦存在时，平面压痕的应力场为复合型奇异应力场，需采用能量型边界开裂准则，即Gmax＝GIC。文献［10］讨论了小摩擦情况下平面压痕临界开裂角、正则化临界载荷以及正则化临界压头宽度等的上下界问题。实际上，对于图3所示的周期阵列压痕模型，依据渐进奇异应力分析理论，在压痕的边界处即压头的角点处存在文献［11－12］给出的相关结论。如平面压痕临界开裂角：

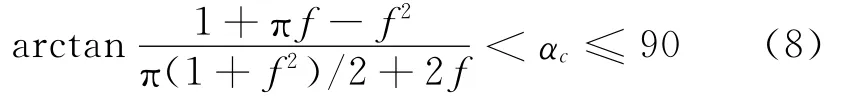
正则化临界载荷：

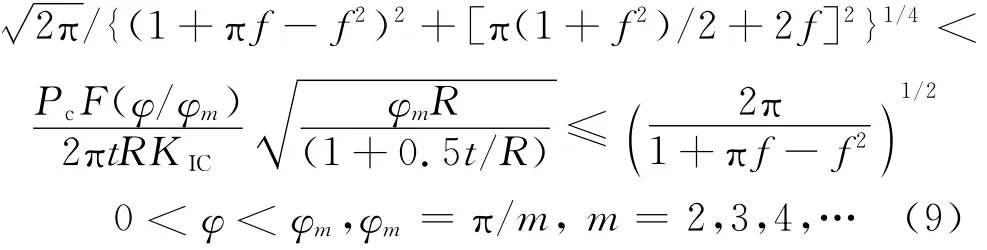
图5和图6给出了（8），（9）式与摩擦系数的关系。

Fig.5 Variation of boundary cracking angle with friction coefficient factor f图5 压痕边界临界开裂角与摩擦系数的关系

Fig.6 Variation of normalized critical load with friction coefficient factor f图6 压痕边界临界开裂载荷与摩擦系数的关系

4 结论

本文利用平面压痕模型分析了圆柱壳周期阵列压痕断裂型破岩机理，在确定柱壳周期阵列压痕应力强度因子的基础上，给出了取芯钻临界载荷的上下界，以及临界开裂角的上下界。通过接触方法诱生奇异应力场的原理，结合平面压痕断裂力学，揭示了压痕边界的断裂型开裂对平齿切割工具破岩行为的贡献。实现了断裂型破岩行为的定量描述。

［1］ 徐西鹏.岩石材料的金刚石锯切研究进展［J］.机械工程学报，2003，39（9）：17－22.

［2］ Nadai A I.Theory of flow and fracture of solids［M］.New York：McGraw－Hill，1963.

［3］ Giannakopoulos A E，Lindley T C，Suresh S.Aspects of connections and life－prediction methodology for frettingfatigue［J］.ActaMaterialia，1998，46：2955－2968.

［4］ Yang B，Mall S.On crack initiation mechanism in fretting fatigue［J］.ASME j.applied mechanics，2001，68：76－80.

［5］ Giannakopoulos A E，Venkatesh T A，Lindley T C，et al.The role of adhesion in contact fatigue［J］.ActaMaterialia，1999，47：4653－4664.

［6］ Xie Y J，Hills D A.Quasibrittle fracture beneath a flat bearing surface［J］.Engineering fracture mechanics，2008，75：1223－1230.

［7］ Xie Y J，Lee K Y，Hu X Z，et al.Applications of conservation integral to indentation with a rigid punch［J］.Engineering fracture mechanics，2009，76：949－957.

［8］ Xie Y J，Hills D A.Quasibrittle fracture beneath a flat bearing surface［J］.Engineering fracture mechanics，2008，75：1223－1230.

［9］ Xie Y J.An analytical method on circumferential periodic cracked pipes and shells［J］.International journal of solids and structures，2000，37：5189－5201.

［10］ 谢禹钧，王伟，王晓华，等.平面压痕开裂极限临界载荷与开裂角［J］.石油化工高等学校学报，2010，23（3）：68－71.

［11］ Xie Y J，Hu X Z，Wang X H.Frictional contact induced crack initiation in incompressible substrate［J］.Engineering fracture mechanics，2011，78：2947－2956.

［12］ Xie Y J，Hu X Z，Wang X H，et al.A theoretical note on mode－I crack branching and kinking［J］.Engineering fracture mechanics，2011，78：919－929.