基于KES测试的织物模型建立和外观动静态模拟

孟宁宁，张瑞云

(东华大学，上海 201620)

织物性能预测体系的建立一直是服装、家纺等纺织企业和织物设计应用研究中亟待解决的一个问题。如果能够在计算机中再现或者预测织物的动静态行为，可大大提高服装或家纺产品在设计、开发等各环节的效率，也有助于实现大规模用户化服装定制。近些年相关力学模型的建立，为织物性能预测系统的实现提供了良好的技术基础，也使织物变形模拟这一织物性能预测的关键技术成为国内外计算机和纺织界的研究者们关注和重视的研究课题。

从20世纪80年代开始，为了更准确真实地模拟织物的变形行为，人们在仿真模型[1]、碰撞响应与检测[2]、积分方法[3]等方面做了大量的研究。但是由于没有与织物本身的力学性能较好地结合起来，当前的织物模型模拟出的织物与实际情况存在较大差距。有研究者[4-6]提出，建立考虑织物拉伸、弯曲和剪切等因素的能量方程，利用稳定状态能量最小的原理模拟出织物的悬垂状态，但这种方法计算复杂且适用范围较小。

本文在弹簧—质点模型的基础上，将模型中弹簧的力学性能与KES测试系统测得的织物基本力学数据结合起来，建立相关数学模型，利用计算机编程较为真实地模拟出了织物的动静态行为。

1 弹簧—质点模型的建立

本文采用能较好模拟织物复杂变形的弹簧—质点模型模拟织物的动静态变形。弹簧—质点模型将织物假设为若干个质点的集合，质点间的相互关系归结为质点间的弹簧作用，弹簧分为三类，结构弹簧、弯曲弹簧和剪切弹簧。如图1所示。

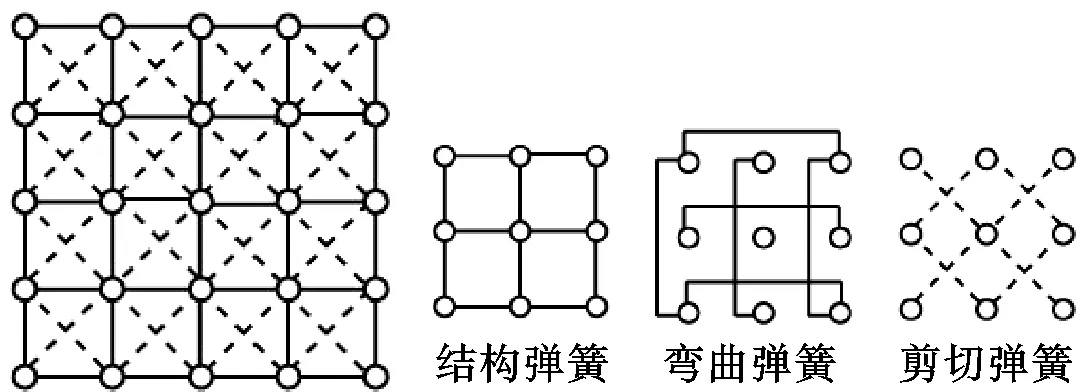
图1 织物模型

模型中的质点是织物质量的载体，用于表现织物的重力，质点在运动中会受到模型内部弹簧力和外力的作用，而呈现不同的状态。这些质点运动状态的总和表现了织物的静态和动态行为。

模型中的三种弹簧在织物模拟中的作用各不相同。其中：

结构弹簧将一个质点和与它直接相连的质点连接。它产生的力用于抵抗织物的拉伸或压缩，保持织物的形状。

弯曲弹簧将中间隔一个质点的两个质点连接，它产生的力用于抵抗织物的弯曲变形，防止织物的不自然的过度弯曲。

剪切弹簧将小四边形中对角线上的两点相连接，它产生的力用于抵抗织物的斜向变形。

这三种弹簧产生的力是约束质点运动的主要作用力，即决定织物运动形态的主要作用力。弹簧的力学行为是线性的，而织物的力学行为是复杂的非线性，如果用单纯的弹簧系数代替织物的力学指标参数，不仅不能模拟出贴近实际的织物形态，而且会出现严重失真。KES测试系统是国际上认可的测试织物基本力学行为的方法。KES测试系统测得的数据能够真实地反映织物的拉伸、剪切和弯曲等基本力学性能，若将这些数据与弹簧的力学，用某种方法结合起来，使织物的力学性能真实地在模型中表现出来，那么模拟出的织物行为也会更贴近实际。

2 模型的参数化

2.1 模型力学参数的计算

KES基本力学性能测试仪可测量得到织物的拉伸曲线、弯曲曲线和剪切曲线，这些曲线真实地反应了织物的力学性能。弹簧—质点模型中弹簧的力学计算公式可以从这些实验曲线中推导得到[7]。

2.1.1结构弹簧力

在KES拉伸测试中，一定的拉伸力施加于矩形试样的一边，然后测得试样的应变，如图2所示。在织物模型中，这样的拉力由结构弹簧承受，假设同一方向上(经向或纬向)上各个弹簧分担的力相同，那么就可由此计算出每个弹簧的力学性能。

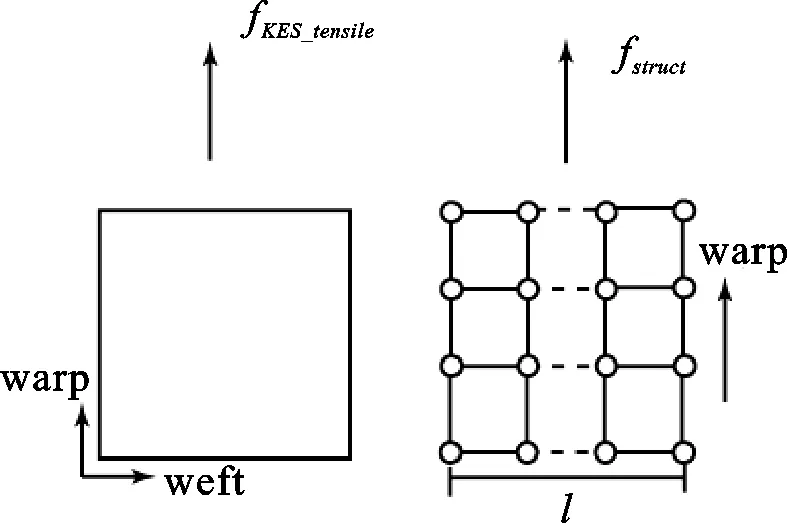
图2 由KES拉伸测试结果计算结构弹簧的受力

以经向为例，计算经向结构弹簧的受力：

(1)

(2)

其中：

fstruct——织物经向在拉伸状态下，每根经向结构弹簧的受力，cN；

Δstruct——织物经向在fstruct的作用下，每根经向结构弹簧的变形量，cm；

fKES_tensile——KES拉伸测试中单位宽度的织物经向所受的拉力，cN/cm；

ε——织物在fKES_tensile的作用下长度方向的应变；

l——模型中织物的纬向长度，cm；

n——模型中织物纬向的节点数；

2.1.2剪切弹簧力

由于织物力学模型中，模拟剪切力的剪切弹簧是沿织物的45°方向，为保证模型的力学能很好地反应织物的实际力学，用来计算剪切弹簧力的实验数据，也应是测试织物45°方向的力得到的。因此，本文不采用KES传统的剪切测试，而是沿织物的45°方向裁剪方形试样，如图3所示，然后在KES的拉伸测试仪上测其拉伸性能，这样得到的测试结果就是织物45°方向的变形和受力。由这个测试结果即可计算出模型的剪切弹簧力。

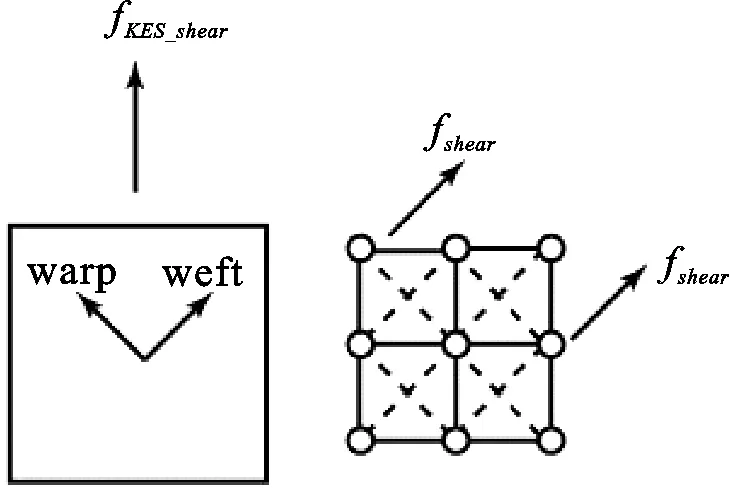
图3 由KES 45°拉伸测试结果计算剪切弹簧受力

计算剪切弹簧的受力：

(3)

(4)

其中：

fshear——织物模型在拉伸状态下剪切弹簧的受力，cN；

Δstruct——织物模型经向在fshear的作用下，每根剪切弹簧的变形量，cm；

fKES_shear——KES 45°拉伸测试中单位宽度的织物所受的拉力，cN/cm；

ε——织物在fKES_shear的作用下长度方向的应变；

l——模型中织物的经向(或纬向)的长度，cm；

n——模型中织物45°方向上的节点数；

2.1.3弯曲弹簧力

在KES测试中，弯曲测试得到的结果是弯曲力矩与试样曲率的曲线，但是计算模型中的弯曲弹簧的力学性能，需要的是弹簧的受力与两端的距离的关系，因此需要将KES弯曲仪测得的结果做相应的转化，将力矩转化为力，将曲率转化为距离，如图4所示。

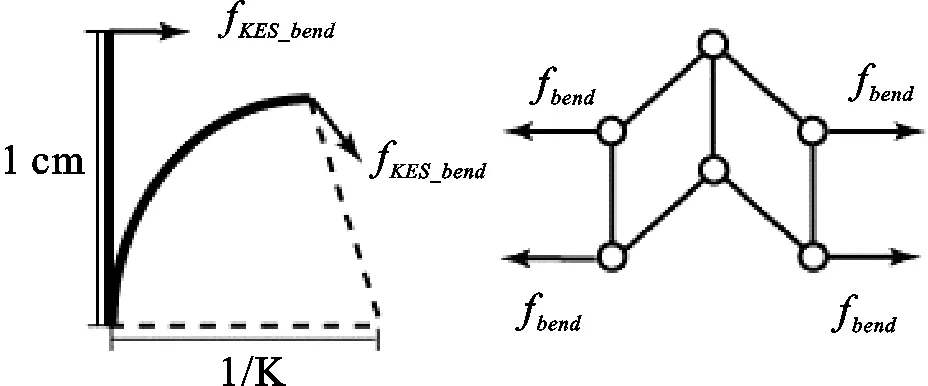
图4 由KES弯曲测试结果计算弯曲弹簧的受力

以经向为例，计算经向弯曲弹簧的受力：

(5)

(6)

(7)

其中：

MKES_bend——KES测试中，单位宽度的织物经向弯曲所受的弯矩，cN·cm/cm；

fKES_bend——KES拉伸测试中单位宽度的织物经向弯曲所受的力，cN/cm；

K——KES弯曲测试中织物弯曲的曲率；

fbend——模型中经向弯曲弹簧所受的力，cN；

Δbend——织物模型经向在fbend的作用下，经向弯曲弹簧两端距离的变化量，cm；

l——模型中织物纬向的长度，cm；

n——模型中织物纬向的节点数；

由公式(1)～(7)可计算出模型中各个弹簧的受力和变形，由受力和弹簧的形变可拟合出弹簧的力学公式。利用这些力学公式，可在织物模型运动的每个时刻，计算出模型中各质点的受力大小和方向，然后由牛顿第二定律，计算出各质点在一个时间步长内的位移。根据这些质点的位移即可得到整个织物的运动状态。

2.2 力学模型的修正

织物本身的力学性能极为复杂，拟合得到的公式只能在一定范围内适用，不能完整体现出织物的力学特性。因此，需要根据织物的力学特性，对该力学模型做适当的调整。

2.2.1弹簧力作用时间

大量实验表明，影响织物悬垂形态的主要因素应是是织物的质量和弯曲性能[8]。但在现有的悬垂状态模拟中，影响织物悬垂性能的主要因素却是拉伸性能。这与弹簧—质点模型中三种弹簧的作用时间有关。

三种弹簧的作用力不应总是同时存在。拉伸弹簧与剪切弹簧应只在织物受拉伸时产生作用，弯曲弹簧应只在织物弯曲时产生作用。而系统只能通过检测弹簧两端的距离来判断是否应该产生力的作用。例如，当织物弯曲时，应只有弯曲力作用，但是在模型中，此时弹簧的两端的距离变短，系统就会计算产生拉伸力、剪切力和弯曲力。而又因为拉伸弹簧产生的力又远大于弯曲弹簧，就使得拉伸性能成了影响织物悬垂形态的主要因素，弯曲性能的影响大大减弱了。

为在模拟系统中，很好的体现弯曲性能对悬垂形态的影响，本文在系统的力学模型做了一下修正：

当弹簧的长度大于原长时，弯曲弹簧的作用力为0，只有拉伸弹簧与剪切弹簧起作用；

当弹簧的长度小于原长时，剪切弹簧与拉伸弹簧的作用力为0，只有弯曲弹簧起作用。

2.2.2失真问题

采用弹簧模拟织物的受力变形时，弹簧会随弹簧受力的增加而不断伸长，这将导致织物出现过度伸长的失真结果。

本文采用在弹簧的临界伸长点，设定较大拉力的方法。即，当弹簧的伸长量超过某一临界值时，弹簧会瞬间产生一个较大的力，将弹簧瞬间拉回临界点以内[9-10]。

这种方法，操作简单，易于运算，而且可以模拟出较为真实的悬垂形态。

3 模拟结果及讨论

3.1 织物静态悬垂的模拟

本文选取了5种具有代表性的织物样品，分别用KES基本力学性能测试仪中的拉伸检测仪—FB1、弯曲性能测试仪—FB2、压缩性能及厚度测试仪—FB3、XCP-1型织物悬垂性测试仪等仪器，测试了织物的性能，其相关性能如表1所示。

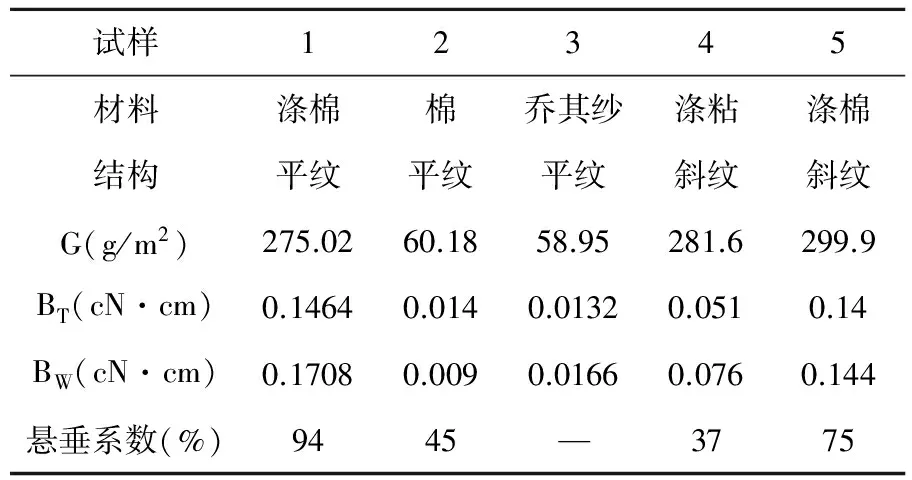
表1 织物试样的基本性能

注：G为试样的平方米克重，BT、BW是试样的经向、纬向弯曲刚度。试样3的经纬密度较小，织物较为透明，难以通过悬垂测试仪测出悬垂系数。

KES基本力学性能测试仪测试五种样品，测试结果除了表1中的基本力学性能指标，还有力学曲线。根据曲线上织物受力与变形量数据，用公式(1)～(7)计算出模型中弹簧的受力和变形量。然后根据弹簧的变形和受力数据用Origin75拟合出织物模型中弹簧的力学公式。

以试样1的经向为例，拟合得到的弹簧力学公式为：

fstruct_warp=163061x2+1994.3x+2.9461

fshear=41136x2+2544.1x+0.6426

fbernd_warp=

其中：

fstruct_warp，fbend_warp，fshear——织物模型中经向结构弹簧、经向弯曲弹簧和剪切弹簧的受力，cN；

x——弹簧的变形量，cm；

利用拟合得到的弹簧力学公式，计算各个时刻模型中质点的受力和位置，模拟出方形织物在圆盘上自然下垂后得到的形态。见图5。

图5 五种方形织物在圆盘上的悬垂形态

表现织物的悬垂形态的参数主要有织物悬垂形成的褶裥数，织物的悬垂面积等。试样1与试样5在5种织物试样中，弯曲刚度最大，最不易于弯曲，所以悬垂形态较其它三种差；试样2、3的弯曲刚度都较小，织物易于悬垂，悬垂面积较试样1、5大；试样4不仅有较小的弯曲刚度，而且有较高的质量，这使得织物易于形成褶裥也易于悬垂，因此5种织物中，试样4形成的褶裥最多，悬垂面积最大，即悬垂效果最好。

3.2 动态模拟

模拟织物变形的弹簧—质点模型中的质点，除了受模型中弹簧的作用，还会受到重力Fgrav、空气阻力fair和风力fwind的作用。

Fgrav=mg/n

fair=cairv

其中：

m——整块织物的质量，g；

n——弹簧—质点模型中质点的个数；

cair——空气阻力系数；

v——弹簧—质点模型中质点的速度，cm/s；

风力fwind也可以算作是空气阻力的一种，在空气阻力的x轴、y轴、z轴方向添加力fwind_x、fwind_y、fwind_z，这样可以在模拟环境中产生一个风的作用力，而且可以通过改变fwind_x、fwind_y、fwind_z的大小调节风向。

fair_x=cairvx+fwind_x

fair_y=cairvy+fwind_y

fair_z=cairvz+fwind_z

将织物悬挂起来，给空气阻力的x轴和y轴方向加一个相同的力，使模拟环境中产生一个与x轴呈45°方向的风力，然后可模拟出织物在风的作用下的动态行为。见图6。

图6 五种织物在风中的形态

织物在风中的形态指标，主要有织物在风向上的位移和织物形成的褶裥数。试样1与试样5弯曲刚度较大，而且较重，在风的作用下，位移小且褶裥少；试样2、3质轻且弯曲刚度较小，所以织物在风的作用下都有较大位移，而试样3的纬向弯曲刚度大于试样2，因此，试样2形成的褶裥数多于试样3。悬垂状态较好；试样4弯曲刚度小而质量大，因此在小位移下形成了褶裥。

4 结论

本文基于弹簧—质点模型和KES测试数据模拟织物的动静态变形行为，根据KES测试数据推导计算弹簧—质点模型中弹簧的力学公式，并根据织物实际力学，对力学公式做修正，限定三种弹簧的作用时间，使得影响实际织物悬垂形态的主要因素—弯曲性能在弹簧—质点模型模拟织物悬垂形态时，也成为主要影响因素[11]。这种方法模拟得到的织物静态悬垂形态不仅将织物的实际力学性能融入模型中，模拟出真实自然的悬垂形态，而且，也体现了影响织物悬垂的主要因素。

另外，本文用较为简单的方法在环境中模拟出了风的作用，并在此基础上模拟出了织物的在风中的动态行为。

在本文研究的基础上，可进一步研究预测织物制成的服装动静形态的系统，以及服装在人体上的动静形态。

参考文献：

[1]Rudomin I J. Simulating Cloth Using a Mixed Geometric-Physical Method [D]. Ph D Thesis, University of Pennsylvania, 1990.

[2]卫巍. 织物模拟中实时碰撞检测方法的研究[D].大连：大连理工大学，2009.

[3]赵龙，兰伟. 基于弹簧—质点模型的织物仿真算法及其性能分析[J]. 现代纺织技术，2007，(3): 6—8.

[4]Au, C.K., Wu, Z., Yuen, M.M.F. Effect of Fabric Properties on Cloth Draping Modeling [J]. Geometric Modeling and Processing,2000: 1—8.

[5]Eischen, J.W., Shigan Deng, Clapp, T.G.. Finite-element modeling and control of flexible fabric parts [J]. Computer Graphics and Applications, 1996: 71—80.

[6]冯毅力，李汝勤. 纺织品悬垂性的计算机仿真[J]. 纺织学报，2001(22):54—55..

[7]纪峰. 织物悬垂性静动态视觉仿真及效果评价[D].上海：东华大学，2005.

[8]周玲玲. 织物力学性能指标与悬垂形态关系研究[D].杭州：浙江理工大学，2010.

[9]纪峰，李汝勤. 基于粒子—弹簧模型的动态服装仿真[J].纺织学报，2004,25(6): 22—24.

[10]吕梦雅，李发明，唐勇，毕卫红. 基于弹簧质点模型的快速逼真的布料模拟仿真[J].系统仿真学报，2009,21(16): 5236—5239.

[11]欧建文，李淑红，梁小平，等.织物柔软度等级评价的BP网络方法[J].山东纺织科技，2009，50(6)：39—42.