广义积分敛散性的一个判别准则

韩建玲

（闽南理工学院信息管理系，福建石狮362700）

1 理论介绍

1.1 无穷小与无穷大［1］

设函数f（x），g（x）在U0（a）上由定义，且g（x）≠0，其中a可以是＋∞，－∞，∞。

如果f（x），g（x）当x→a都是无穷小（或都是无穷大）时，称f（x）是g（x）的高阶无穷小（f（x）是g（x）的低阶无穷大或g（x）是f（x）的高阶无穷大）。

如果f（x），g（x）当x→a都是无穷小（或都是无穷大）时，称f（x）与g（x）是同阶无穷小（或同阶无穷大）。

1.2 无穷积分敛散性的判定［2］

设函数f（x）在区间［a，＋∞）连续，且f（x）≥0。若x→∞时f（x）是的高阶无穷小，则积分收敛，否则积分发散。

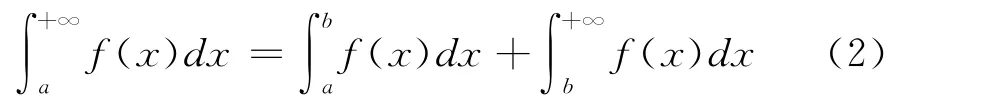
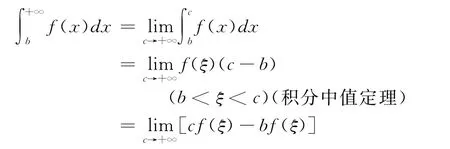
因为b＜ξ＜c，c→＋∞，于是ξ→＋∞。

收敛。

1.3 瑕积分敛散性的判定

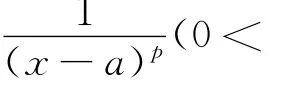
2 例题说明

因此原积分收敛。

3 结束语

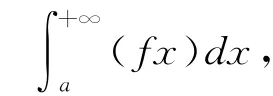
［1］刘玉琏，傅沛仁，等.数学分析讲义：第五版［M］.北京：高等教育出版社，2008：116－117.

［2］云士伟，许 超，等.无穷小的阶在计算中的应用［J］.洛阳工业高等专科学校学报，2002（9）：26－27.