破损船舶拖带计算最优化方法

陈生春 ，苗兰森 ，任 凯

（1.海军工程大学 船舶与动力学院，湖北 武汉 430033；2.海军司令部驻天津地区防救军代室 天津 300042）

破损船舶拖带计算最优化方法

陈生春1，苗兰森2，任 凯1

（1.海军工程大学 船舶与动力学院，湖北 武汉 430033；2.海军司令部驻天津地区防救军代室 天津 300042）

运用非线性规划的方法对满足破损船舶安全性要求的可行航速下的拖缆参数进行优化计算，并通过目标决策方法选择最优航速及拖缆参数方案，对于方案的可用程度给出了定量的评价，提供了破损船舶拖带计算的一种方法。

船舶；拖带；计算；方法

船舶拖带是一项重要的航运任务，船舶的海上拖带要严格组织，制定周密的计划，并进行缜密的计算，遵循各种规范。尽管各国对船舶拖带都给予了充分的重视，可拖航事故还是不断发生。根据日本拖航委员会的一份报告所举事例，仅1974年9月—1975年2月间，在拖带中发生断缆，断端环和使被拖船只遭受损坏和毁坏的竟达13次之多，而实际的事故远不止这些[1]。英阿马岛海战中，英军“谢菲尔德”号驱逐舰被导弹击中没有立即沉没，而是在后来拖航回本土过程中沉没。对破损船舶拖带往往在出现触礁、搁浅等事故之后进行，此时稳度下降幅度较大，受气象条件等客观因素的限制，这除了要考虑能否拖，如何拖，安全拖的问题，还要根据客观条件研究合理拖，尽快拖。因此所进行的计算要综合各方面的因素，给出最优结果[5]。

船舶的海上拖带与拖航的速度大小，拖缆直径，拖缆强度与长度，拖船的负荷，被拖船的稳性、受损情况，当地气象、海况等诸多因素有关，且这些因素相互制约。对船舶拖带所进行的专门计算主要包括：拖带速度，拖缆参数，拖缆在风浪中的猛拉作用，以及拖船的允许转速[3]。在实践中通常的方法是按近似公式由拖力确定拖航速度，并对拟定的拖缆参数，检验其强度及悬垂度，以及对被拖船的安全性要素进行校核。这种方法仅能从计算的结果中得出各项因素的边界值，并依此设计拖航的速度，选用拖缆的规格等，当被拖舰存在破损时，情况比较复杂，其计算结果仅可作为基本参考。运用计算机可以对拖航要素进行规划，并对可行的结果通过目标决策的方法进行分析进而得出最优方案，下面将结合具体问题进一步说明。

1 非线性规划法确定可行的拖航速度及拖缆参数

1.1 问题背景

某货轮发生搁浅，事故导致左舷出现大破口，并造成相应舱室淹没，相邻舱室均已加固支撑，货轮进水情况得到了暂时控制，经测算其稳度因损害下降了0.06 m。失事海区风力4～5级，5级海情。根据需要，由一拖船将其拖回，拖缆有以下规格可用：32.5 mm，39 mm，52 mm，65 mm。

破损船的主要参数：该船长（L）164 m，宽（B）16.8 m，吃水（T）5.7 m，排水量（D）6 138.75 t，重心距基平面高（Zg）7.98 m，拖缆作用点距离基平面高（ZPT）14.3 m，初稳度（h）0.78 m。

1.2 拖带计算的主要内容

1.2.1 被拖舰船的拖曳阻力及被拖舰总阻力

拖船的推力（Pe）用以平衡自身阻力（R1）和被拖舰总阻力（R）。采用解析法计算总阻力，总阻力等于拖曳阻力（RT）与拖缆水中阻力（R3）之和，而拖曳阻力主要取决于以下几个因素：被拖船的自身水阻力（R2）、空气阻力（R空）、波浪阻力（R波）、自由旋转或制动螺旋桨阻力（R桨）。

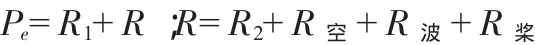
R1根据拖船的阻力特性确定；

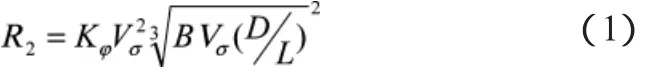
式中：Kφ为船形系数，取值 0.001 164；Vσ为拖速（kn）。

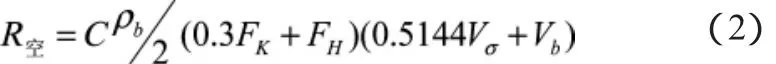
式中：C为空气阻力系数，迎风时1.0～1.2，风向角为30°时 1.6～1.8，风从正横后方来时 0；ρb为空气密度，取 0.121 kg·s2/m4；FK为船体正面受风面积，即船体水上部分在舯船肋骨面上的投影；FH为上层建筑和桅杆正面受风面积；Vb为风速，根据《浦氏风级表》4级6 m/s，5级9 m/s。

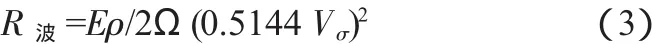
式中：E为波浪阻力系数，1×10-4×级数；ρ为海水密度，0.104 kg·s2/m4；Ω 为船体湿表面积，Ω =(1.36T+1.13δB)L，(δ取值范围为 0.53～0.55)；

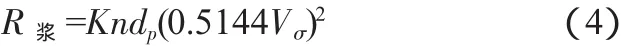
式中：K为系数，制动桨取2.24，自由旋转取0.78；n为螺旋桨数目。

拖缆的水中阻力：

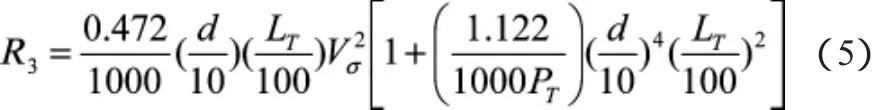
1.2.2 拖缆参数的确定方法

拖缆参数的确定与拖曳阻力有关，可以认为拖缆所承受的拉力等于被拖船的拖曳阻力。而拖缆规格的确定根据要求应保证至少6倍的储备强度，可依据式（6）计算：

拖缆长度（LT）应考虑拖缆在风浪中的猛拉作用，为了保证拖缆不致在拖航中受外力冲击时拉断，因此应保证拖缆具备一定的悬垂度（H），拖缆的悬垂部分能吸收外来的冲击。悬垂度的经验公式为：

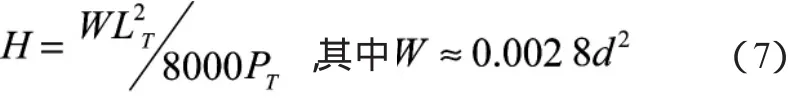
拖缆的悬垂度应控制在8～15 m，拖力PT=RT。特殊情况下，拖缆的最小长度为，其中：C取3.0～3.3；Ni为拖轮的指示马力。

1.2.3 破损舱安全性要求

破损舱壁暴露于海水中，除了受到静水压力外，还要承受与速度关系密切的动水压力作用，可以测算，动压力与速度的平方成正比，当航速提高时，破损舱舱壁将承受较大的水压力，因此必须对隔墙加固。

通常加固损管木受压许用应力[σ许]为100～150 kg/cm2，支柱的许用受力如表1。

表1 支撑受力情况

支撑数目N可由下式推出：

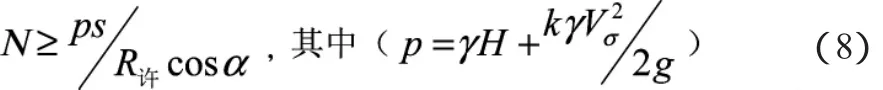
式中：γ为海水密度1.04 t/m3；k=1.12；s为舱壁的浸水面积；α为支撑角度，通常为45°。

1.2.4 被拖船的稳度变化

拖力的大小直接影响到被拖船的稳性，其作用相当于在高处增加载荷，拖力垂直方向分力对于被拖舰的稳度影响较大，初稳度的变化应不大于30%h满，同时，它的横向分力在转向时产生倾斜力矩，因此也应控制转角。

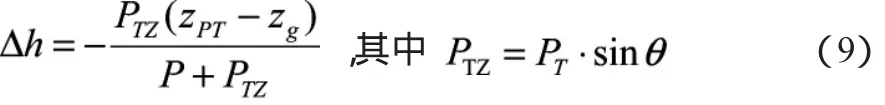
式中：θ为拖力与水平面夹角，可取45°。

1.2.5 拖船最高主机允许转速的确定

拖船的主机允许转速确定了拖带航速的上界，这一允许转速可根据总阻力确定，通过拖船的推力特性求出，本问题中拖船的实际航速不超过13 kn，这也与破损舱壁允许受力有关。

1.3 模型建立并求解

1.3.1 目标函数的建立

根据 1.2 中实际问题的分析，设[Vσ，d，LT]=[x1，x2，x3]=X，由于拖力即拖曳阻力与拖航的安全性存在不可分的联系，可以定义目标函数min f[X]=R=RT+R3，即代入已知数据后：

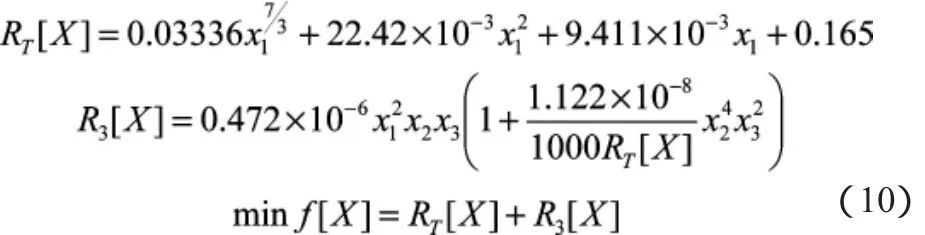
1.3.2 约束条件及边界条件

被拖船稳度Δh约束：

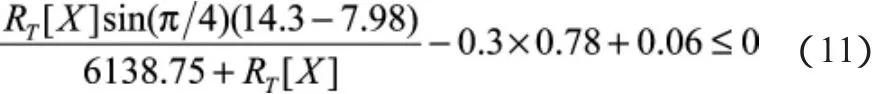
破损舱舱壁安全性要求约束ΔR许：

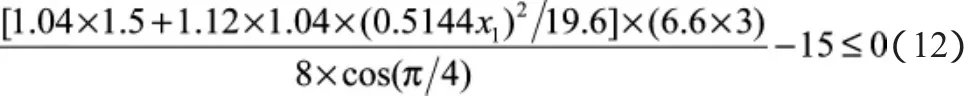
拖缆强度Δd约束：

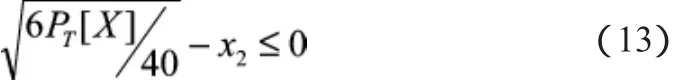
拖缆悬垂度约束：

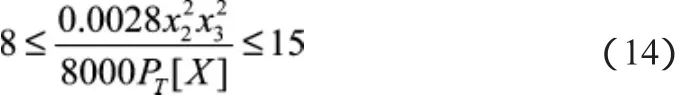
边界条件约束：x1=[1，2，3，4，5，6，7，8，9，10，11，12，13]，x2=[32.5，39，52，65]，x3≥49.4。

1.3.3 模型求解

此非线性规划问题的求解是比较复杂的，x1、x2的取值离散化，根据实际问题需要，每个x1均可作为边界约束条件取值得到最优的x2，x3，对这一规划的求解可借助Matlab中的优化工具箱求解完成。其结果如表2。

2 多目标决策在方案最优选定中的应用

通过1.3求解得到可行方案，从中选取最优方案，这是多目标决策问题，在拖航的实际问题中，首先应保证生命力的各项指标，在这一前提下尽量提高航速，选用规格、长度合适的拖缆。这需要对各方案量化排序，选择综合指标最优的方案。

2.1 决策矩阵的构造

2.1.1 构造初始决策矩阵

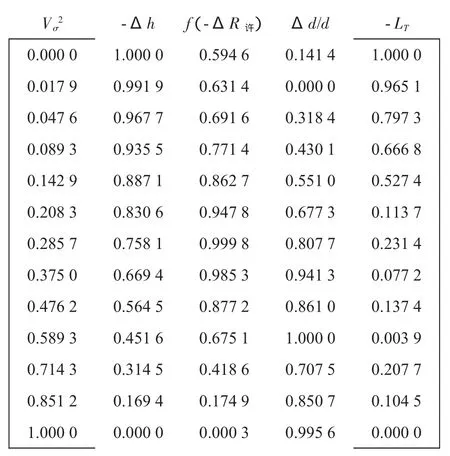
初始决策矩阵的建立首先要选定目标集，目标分为成本型目标和效益型目标，根据拖航实际问题，选定效益型目标：Vσ2，f(-ΔR许)（ΔR许的正态分布密度），成本型目标：Δh，Δd/d，LT，对于成本型目标，数值愈小愈好，效益型则相反。采用Vσ2作为目标是因为拖力等参数与航速的平方成正比，且拖力于其他指标具有不可分的联系；-Δh表示相对于30%h满减小稳度值；选择ΔR许的正态分布密度，是期望在满足破损舱壁受力需要的情况下选用较为合适的ΔR许。下面为初始决策矩阵A初：

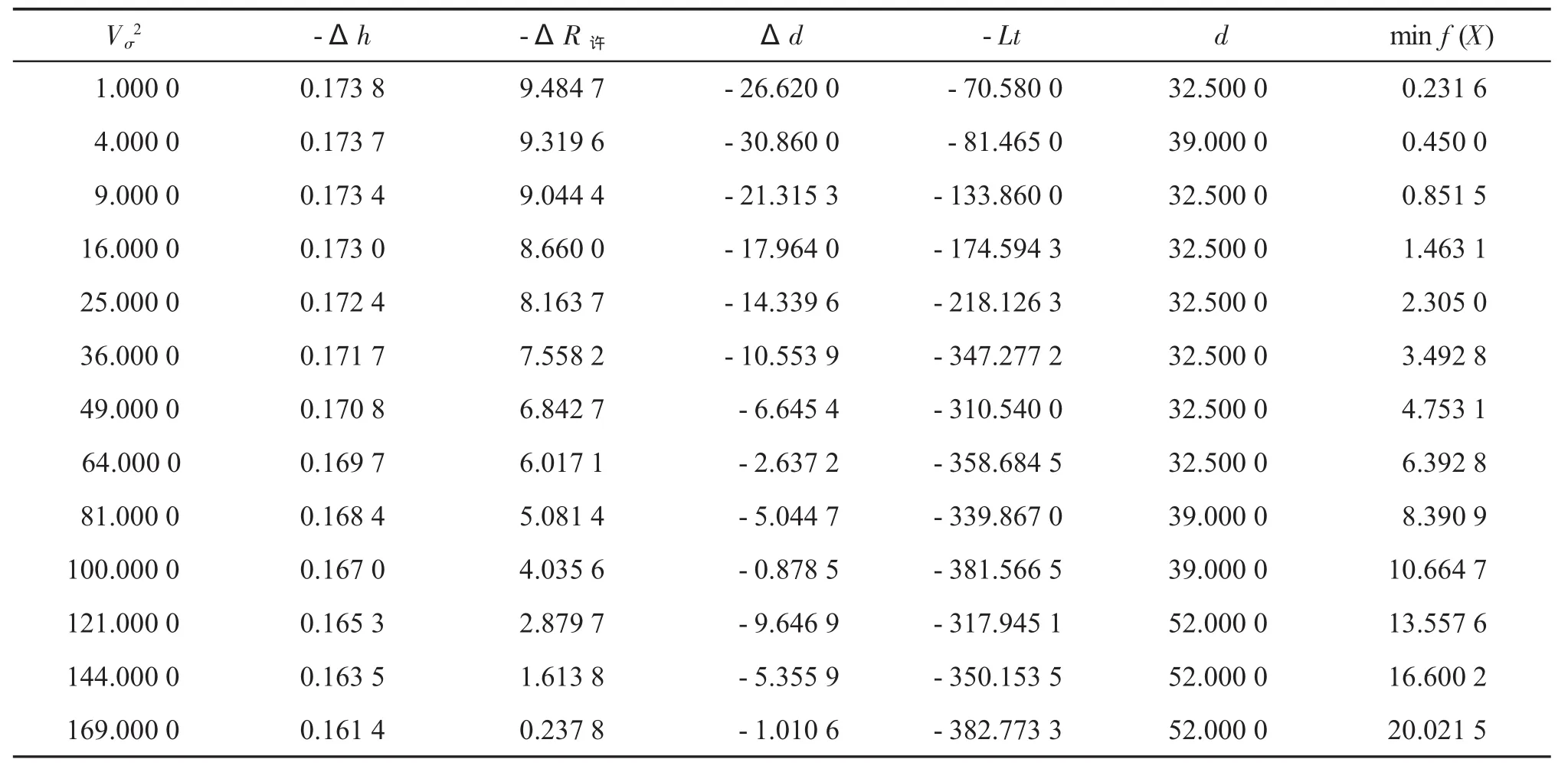
表2 不同拖速下的参数值

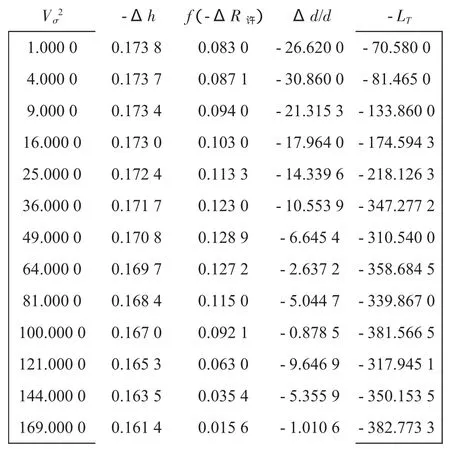
2.1.2 对初始决策矩阵规范化

对于初始决策矩阵需要将目标元素规范化，具体方法是根据成本型和效益型特点。

效益型目标规范化公式：

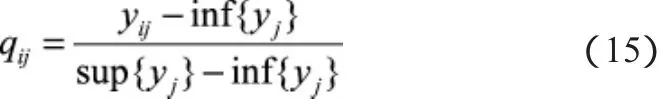
成本型目标规范化公式：

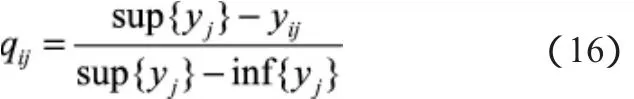
规范化后的初始决策矩阵A如下：

2.2 权矩阵与目标权重向量的建立

2.2.1 专家评判矩阵的建立

多目标决策的一个重要的参考信息，即目标的相对重要性，多数分析方法通过对各目标的属性加权反映各目标的相对重要性，即愈重要的目标权重愈大。采用层次分析法综合专家意见建立专家评判矩阵，目标的相对权重采用标度的方法求出（见表3），并对评判的一致性进行检验。

表3 权重表

建立专家评判矩阵如下：

对此评判矩阵进行一致性检验，所谓一致性是评判矩阵中的因素两两比较时很难做到判断尺度的完全一致，这就要对得到的评判结果进行一致性检验，具体方法是求解评判矩阵的最大非零特征值，该特征值理想状态下应等于矩阵的维数，在实际应用中应放宽对高维评判矩阵的要求，引入指标C.R=C.I/R.I≤0.1 来判断一致性，其中 C.I=(λmax-n)/(n-1)，R.I与矩阵维数关系如表4[2]：

表4 维数与R.I.的关系

这样根据矩阵最大非零特征值λmax=5.440 4求得一致性指标C.R=0.098 3＜0.1，故可以认定该矩阵满足一致性条件。

2.2.2 构造目标权重向量

采用方根法求得反映目标相对重要程度的目标权重向量，其方法是对每一指标求其几何平均值，再归一化处理。求得的目标权重向量ω为：

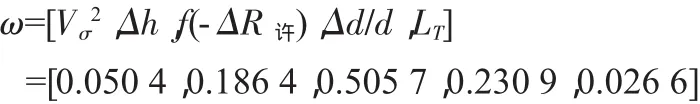
2.3 对方案构造目标效益矩阵形成最优方案

将前面建立的决策矩阵A与目标权向量ωT相乘，即可得到各方案的效益值，即综合指标U：

可见拖航航速在8 kn左右的方案最优。

3 结论

（1）目标权重向量反映了拖带过程中，安全性的重要地位；（2）在充分重视拖航安全的前提下，效益值反映了最佳航速与拖缆参数的最优方案；（3）效益值客观反映了破损舰船拖航航速过大对拖航安全极为不利，通常不超过10 kn。

[1]浦金云,邱金水,程智斌.舰船生命力[M].北京：海潮出版社,2001.

[2]胡运权,等.运筹学[M].北京：清华大学出版社,1990.

[3]邱金水,浦金云,陈兆良.舰船损管监控系统与损管训练[M].武汉：海军工程大学,2001.

[4]曾凡明,等.舰船阻力与推进[M].武汉：海军工程大学,1999.

[5]蔡一轮,浦金云.失事船舶拖带方案的优化决策模型[C]//救捞专业委员会03年学术交流会论文集,2003：18-23.

[6]陈生春,任凯,程智斌.拖缆强度校核的随机模拟方法[J].海军工程大学学报,2006,16(6)：58-60.

Optimal Towline Calculation of Distressed Vessel

CHEN Sheng-chun1,MIAO Lan-sen2,REN Kai1
(1.College of Naval Architecture and Marine Power,Naval University of Engineering,Wuhan Hubei 430033,China;2.The Navigation Guarantee Department of Chinese Navy Headquarters,Tianjin 300042,China)

The nonlinear rule was used to make an optimized calculation about the parameters of towline which suits to safety of distressed vessel,which created the best scheme of ship speed and towline parameters by multiple target decision-making rule.The quantitative evaluation about the feasibility and calculating way about the parameters of distressed vessel’s towline were given.

vessel;towline;calculation;method

U661.32

A

1003-2029（2012）02-0036-04

2012-01-29

陈生春（1960-），男，硕士，副教授，主要从事船舶安全技术与工程研究。Email：liuhui503@126.com